Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Методика комплексной сравнительной оценки психофизиологического состояния обследуемых
Аннотация:Рассмотрена методика комплексной сравнительной оценки параметров психического и физиологического со-стояний обследуемых в фиксированный момент и во временной динамике при наличии и отсутствии требований к значениям частных диагностических показателей с помощью отдельных интегральных диагностических показателей и их систем.
Abstract:The procedure of the complex comparative estimation of the parameters of mental and physiological state of men investigated at the fixed moment of time and in the temporary dynamics in the presence and the absence of requirements for the values of particular diagnostic indices with the aid of the separate integral diagnostic indices and their systems is examined.
| Авторы: Ермаков А.Е. (alerma@rambler.ru) - Военно-медицинская академия им. С.М. Кирова, г. Санкт-Петербург, г. Санкт-Петербург, Россия, кандидат технических наук | |
| Ключевые слова: классификация обследуемых, коэффициенты сравнительной ценности частных показателей, психологические (физиологические) требования, интегральный диагностический показатель, частный диагностический показатель, психологическая (физиологическая) характеристика |
|
| Keywords: the classification of men investigated, the coefficients of the comparative value of particular indices, psychological (physiological) requirements, integral diagnostic index, particular diagnostic index, : psychological (physiological) characteristic |
|
| Количество просмотров: 11692 |
Версия для печати Выпуск в формате PDF (5.35Мб) Скачать обложку в формате PDF (1.27Мб) |
Проблема разработки новых типов интегральных диагностических показателей (ИДП), пред- назначенных для применения в физиологии, психологии, социологии, клинической медицине, профессиональном отборе, не утратила своей актуальности, несмотря на многолетние исследования специалистов [1, 2]. Часть используемых в медицине, особенно в физиологии, интегральных показателей имеет вид так называемых физиологических индексов, эвристически сконструированных с помощью арифметических операций над результатами физиологических измерений (индекс реактивности нервной системы Кердо, физиологический индекс Богомазова, индекс Руфье и др.). Такие показатели обычно применяются для решения специфических диагностических задач – определения состояния отдельных физиологических систем организма человека, уровня их резервных возможностей и пр. ИДП для комплексной оценки психологических и социально-психологических характеристик обследуемых в психологии и социологии создаются на основе содержательного и статистического анализа связей между различными тестовыми шкалами, факторами и внешними критериями [1]. В социологии роль ИДП играют социологические индексы, используемые для измерения социальных установок респондентов, анализа межличностных отношений и пр. Широко применяются ИДП и для оценки качества жизни больных и здоровых людей, а также при исследовании уровня общественного здоровья населения. Многие ИДП строятся на основе использо- вания статистических методов анализа данных и выявления зависимостей – корреляционного, регрессионного, факторного анализа и т.п. Все более широкое распространение получают процедуры формирования ИДП и диагностических заклю- чений на основе методов логического анализа данных, выявления закономерностей и зависимостей. В то же время многообразие задач, возникающих и решаемых специалистами в ходе психологической и физиологической диагностики, социометрических исследований, делает актуальным и другой, более универсальный подход к интеграции результатов измерения разнородных психологических, физиологических и психофизиологических характеристик (ПФХ) обследуемых. Этот подход не зависит от номенклатуры и особенностей частных диагностических показателей (ЧДП) и применяемых для их измерения шкал. Достаточно измерить множество разнородных ПФХ посредством прогностичных ЧДП, а главным требованием к ним является парная экспертная сравнимость ценности выбранных ПФХ в контексте решаемой диагностической задачи. Рассматриваемая методика комплексной сравнительной оценки психологического и физиологического состояния (ПФС) обследуемых и реализующая ее автоматизированная система (АС) базируются на использовании нескольких систем ИДП, которые строятся на основе ЧДП, применяемых для анализа ПФХ обследуемых с учетом сравнительной значимости этих ПФХ в контексте задачи. Сравнительная значимость ЧДП описывается коэффициентами сравнительной ценности (КСЦ), формируемыми с помощью специальной процедуры их экспертно-алгоритмического парного сравнения [3]. Сравнительная оценка ПФС обследуемых с помощью методики и данной АС проводится как при наличии априорно заданных экспертных требований к значениям ЧДП, разделяющих множества их значений на два или более непересекающихся подмножеств, так и при их отсутствии. Оценка и сравнение ПФС обследуемых могут осуществляться в фиксированный момент и во временной динамике. Результатом применения рассматриваемой методики являются значения ИДП, позволяющие специалистам: – ранжировать обследуемых по их ПФС в соответствии с целью решаемой задачи при наличии и отсутствии априорных требований к значениям ЧДП с учетом их сравнительной значимости; – распределить обследуемых по нескольким группам (классам ПФС), предъявляющим непересекающиеся между собой требования к значениям ЧДП; – оценить совокупную динамику изменения ПФС обследуемых во времени и ранжировать их с учетом этой динамики; – оценить интегральную степень близости ПФС обследуемых к идеальному состоянию. Ключевые элементы методики, процедуры расчета КСЦ частных показателей, системы статических и динамических ИДП реализованы в комплексе прикладных программ «Автоматизированная система для расчета интегральных показателей оценки психического и физиологического состояния человека» (Свид. об офиц. регистр. прогр. для ЭВМ № 2003611034 от 29.4.2003 г.). Программное обеспечение АС разработано на алгоритмическом языке Microsoft Visual Basic, снабжено контекстно-зависимой справочной системой на базе файлов формата html. Итак, в ходе проводимого обследования все респонденты оцениваются по заранее отобранному экспертами набору ПФХ. Каждая ПФХ оценивается с помощью одного или нескольких ЧДП. В контексте диагностической задачи эти ПФХ имеют некоторую значимость, которую специалисты способны сравнить. В результате обследования каждому респонденту сопоставляется множество значений ЧДП, оценивающих наличие или степень выраженности у него этих ПФХ. Области допустимых значений ЧДП могут задаваться с помощью односторонних, двусторонних ограничений, списков допустимых диапазонов или допустимых значений. На первом этапе реализации методики экспертами формируются измерительные шкалы, используемые для парного сравнения значимости ЧДП, и задается отношение частичной транзитивности (ОЧТ) парных оценок, применяемое в АС для снижения вопросной нагрузки на эксперта и потенциальной противоречивости формируемых КСЦ. На втором этапе АС рассчитывает КСЦ, количественно характеризующие сравнительную значимость исследуемых ПФХ и ЧДП. На третьем этапе производится расчет выбранных экспертом ИДП и их систем на основе значений ЧДП, их КСЦ, а в случае необходимости предъявляемых к значениям ЧДП требований. В результате с помощью найденных значений ИДП сравнивается ПФС обследуемых и производится их ранжирование в соответствии с целью и особенностями проводимого обследования. Практическая реализация первого и второго этапов методики описывается в [3–5]. Рассмотрим третий этап. Полагаем, что ПФС обследуемых в диагностических задачах сравнивается посредством s ПФХ, для оценки которых используется n≥s ЧДП {p1, …, pn}. Перед началом обследования экспертом могут быть заданы границы, разделяющие множества значений ЧДП на подмножества допустимых и недопустимых значений. Области значений ЧДП задаются с помощью односторонних числовых ограничений, двусторонних ограничений, в виде списка допустимых значений. Области могут задаваться с помощью дискретной числовой, непрерывной числовой или качественной шкалы. В зависимости от целей обследования априори могут также задаваться и непересекающиеся области значений, соответствующие различным состояниям организма обследуемых. Обозначим через Qiдоп множество допустимых значений ЧДП pi, Qiнед – множество его недопустимых значений в контексте решаемой диагностической задачи. Очевидно, что Ui=QiдопÈQiнед, Qiдоп=Ui\Qiнед, Qiнед=Ui\Qiдоп, где Ui – множество всех возможных значений ЧДП pi; \ – операция исключения Qiдоп(Qiнед) из Ui; È – операция объединения множеств значений ЧДП. Для комплексной оценки соответствия обследуемых предъявляемым психофизиологическим требованиям (ПФТ) в методике и АС используются несколько ИДП и их систем, которые выбираются пользователем в зависимости от целей исследования, особенностей диагностической задачи и исходных данных. Рассмотрим первую систему ИДП методики, реализованной в АС. Обозначим через Р1+ ИДП, оценивающий степень соответствия обследуемого предъявляемым ПФТ, Р1- – ИДП, оценивающий степень его несоответствия этим ПФТ, Р1Δ – ИДП, описывающий соотношение степеней соответствия и несоответствия обследуемого предъявляемым ПФТ. Система ИДП {Р1+, Р1-, Р1Δ} формируется по следующим правилам: Р1+= Р1-= Р1Δ=Р1+–Р1-. Из (1) видно, что в состав Р1+ входят КСЦ {wi} ЧДП {pi}, значения которых для обследуемого принадлежат (Î) {Qiдоп}, а в состав Р1- – КСЦ {wj} ЧДП {pj}, значения которых Î {Qjнед}. По окончании расчетов обследуемые ранжируются по величине Р1Δ. Изначально Р1+=Р1-=0. Предложенная система ИДП позволяет перейти от несопоставимых разнородных значений нескольких ЧДП к работе с их КСЦ, описывающими сравнительную ценность ЧДП в контексте решаемой диагностической задачи. Множество возможных значений Р1Δ описывается интервалом [–Р1max; Р1max], где Р1max= =w1+w2+ …+wn. Преобразуем ИДП Р1Δ к виду, более удобному для анализа, перейдя от него к ИДП Р2Δ=Р1Δ+Р1max. Множеством значений Р2Δ является интервал [0; 2Р1max], что позволяет, помимо ранжирования обследуемых, говорить и о степени достижения каждым из них наилучшего значения этого ИДП, равного 2Р1max. Также можно разделить множество возможных значений Р2Δ на интервалы, соответствующие различным степеням реализации потенциально возможных значений этого ИДП, например, [0; 0,4Р1max], ]0,4Р1max; 0,8Р1max], ]0,8Р1max; 1,2Р1max], ]1,2Р1max; 1,6Р1max], ]1,6Р1max; 2Р1max], сопоставив им значения (уровни) «очень низкий», «низкий», «средний», «высокий», «очень высокий», а по формуле Pr=50´Р2Δ/Р1max можно определить, какой процент Pr составляет найденное для обследуемых значение ИДП Р2Δ от его потенциально возможного наилучшего значения 2Р1max. Если выполнить нормирование Р1Δ и Р2Δ, разделив их на Р1max, то множества возможных значений нормированных ИДП Р1нΔ и Р2нΔ примут вид [–1; 1] и [0; 2]. Слегка изменив систему (1), можно использовать ИДП для оценки интегральной степени близости значений ЧДП обследуемых к каждому из нескольких состояний ПФС {Gk, k=1, ..., j} – различных заболеваний, состояний «болен», «здоров», «компенсированные нарушения ПФС» и пр. Для этого, исходя из специфики задачи, области значений {Qi} ЧДП {pi} разбиваются экспертом на непересекающиеся подобласти {Qik, k=1, ..., j}, отвечающие {Gk}. Система ИДП {Р3k, k=1, ..., j} в этом случае формируется по правилам: Р3k= Формула означает, что КСЦ wi ЧДП pi добавляется в тот ИДП Р3k, в область значений Qik которого попадает измеренное у обследуемого значение pi. Решение об отнесении состояния обследуемого к одному из {Gk} принимается по максимуму ИДП {Р3k, k=1, ..., j}. До начала сравнения {Р3k=0, k=1, ..., j}. Если КСЦ не использовать, то есть " i: wi=1, то Р3k имел бы смысл числа ЧДП {pi}, значения которых принадлежат {Qik}. При использовании системы ИДП (1) не учитываются величины превышений значениями ЧДП {pi} предъявляемых к ним требований и степени их несоответствия этим требованиям. Термин «превышение» для различных ЧДП может иметь смысл: как больше, так и меньше некоторого значения. Эту проблему решает система ИДП {Р4+, Р4-, Р4Δ}. Для ее применения после первоначального измерения значения всех ЧДП пересчитываются в единую числовую шкалу. ИДП этой системы формируются по правилам: Р4+= Р4-= Р4Δ=Р4+–Р4-; Δpi = min{|pi – piгр|}. В состав Р4+ входят {Δpi} тех ЧДП {pi}, значения которых для обследуемого входят в {Qiдоп}, в состав Р4- входят {Δpj} для ЧДП {pj}, значения которых попадают в {Qjнед}. Через min{|pi–piгр|} обозначен модуль разности измеренного значения ЧДП pi и ближайшего к нему или единственного граничного значения piгр, разделяющего множества Qiдоп и Qiнед. КСЦ {wi} ЧДП {pi} в данной системе ИДП не используются для предотвращения ситуаций вида Δpi=15, wi=2, Δpm=2, wm=15ÞΔpi´ ´wi=Δpm´wm=30, когда разности значений ЧДП и их КСЦ взаимно компенсируются. Рассмотрим теперь ряд систем ИДП вида {P-(Δt), P+(Δt), РΔ(Δt)}, используемых в методике и АС для исследования динамики изменения ПФС обследуемых во времени. ИДП P-(Δt) характеризует в целом негативную составляющую динамики изменения ПФС обследуемого, ИДП P+(Δt) – позитивную составляющую, а ИДП РΔ(Δt)=Р+(Δt)– –Р-(Δt) – баланс между позитивной и негативной тенденциями динамики ПФС. При использовании этих систем ИДП обследуемые разбиваются на группы: 1) имеющих позитивную динамику изменения значений ЧДП (P-≈0 [P-0 [Р+>d], РΔ>0 [РΔ>d]); 2) лиц, позитивная динамика изменения значений ЧДП у которых превышает негативную (P->0 [Р->d], P+>0 [Р+>d], РΔ>0 [РΔ>d]); 3) лиц, не имеющих позитивной и негативной динамики изменения значений ЧДП (P-≈0 [P-0 [Р->d], P+>0 [Р+>d], РΔ≈0 [РΔ0 [Р->d], P+≈0 [P+0 [Р->d], P+>0 [Р+>d], РΔ<0 [РΔ<–d]), d>0 – минимальное значимое отклонение значений ИДП от нуля. Обозначим через pxi значение ЧДП px, измеренное в момент ti, i – порядковый номер обследования по времени его проведения, Δt=ti–ts – временной интервал между сравниваемыми обследованиями, ti>ts (Δt>0). Считаем, что в период Δt сравнительная ценность {wx} всех ЧДП {px} не меняется. Первая система ИДП для оценки динамики ПФС обследуемых {Р5+(Δt), Р5-(Δt), Р5Δ(Δt)} формируется по правилам: Р5+(Δt)= Р5-(Δt)= Р5Δ(Δt)=Р5+(Δt)–Р5-(Δt), Δt>0. Символом ²›² обозначен результат сравнения «значение pxi ЧДП px лучше значения pxs», символом ²‹² – результат «значение pyi хуже значения pys». До начала сравнения значений ЧДП Р5+(Δt)=Р5-(Δt)=0. КСЦ {wx} ЧДП {px}, для которых значения pxi=pxs или |pxi–pxs|0, в Р5+(Δt) и Р5-(Δt) не включаются. Данную трактовку результата сравнения значений ЧДП › в практических задачах обычно заменяют на «значение pxi лучше значения pxs и |pxi–pxs|>d(dx)», а результата ‹ на «значение pyi хуже значения pys и |pyi–pys|>d (dy)», где d(dx, dy)>0 – порог различения отличий между значениями pxi, pxs (pyi, pys), который зависит от используемой измерительной шкалы, особенностей решаемой задачи и ЧДП. В методике и АС используется и система ИДП {Р6+(Δt), Р6-(Δt), Р6Δ(Δt)}, формируемая по правилам: Р6+(Δt)= Р6-(Δt)= Р6Δ(Δt)=Р6+(Δt)–Р6-(Δt); Δpx= |pxi–pxs|; Δpy=|pyi–pys|, Δt>0. До начала сравнения значений ЧДП Р6+(Δt)= =Р6-(Δt)=0. Величины {Δpx}, для которых значения pxi=pxs или |pxi–pxs|0, в Р6+(Δt) и Р6-(Δt) не включаются. В этой системе ИДП значения {pxi, pxs} всех ЧДП {px} заранее должны быть пересчитаны в единую измерительную шкалу – Т-баллов, процентилей и др. Однако не всегда при проведении интегральной сравнительной оценки ПФС обследуемых для используемых ЧДП нужно и можно задавать априорные требования к их значениям – области допустимых и недопустимых значений. В этих случаях в методике и АС используются ИДП P7, P8 и P9, позволяющие сравнить ПФС нескольких обследуемых при отсутствии априорных требований к значениям анализируемых ЧДП. Итак, пусть имеется m обследуемых {o1, …, om}, значения {pxi, x=1, …, n, i=1, …, m} аналогичных ЧДП {px, x=1, …, n} которых сравниваются между собой для формирования интегральной оценки их ПФС. ИДП P7 – суммарная мера доминирования по значениям {pxi, i=1, …, m} ЧДП {px, x=1, …, n} каждого из обследуемых {o1, …, om} над всеми остальными обследуемыми с учетом сравнительной ценности ЧДП, описываемой их КСЦ {wx, x=1, …, n}, в контексте задачи. ИДП P8 – суммарная мера доминирования по значениям ЧДП каждого обследуемого над всеми остальными с учетом соотношения пар значений {(pxi, pxs), i=1, …, m–1; s=i+1, …, m} ЧДП {px, x=1, …, n} по абсолютной величине при использовании для всех ЧДП единой измерительной шкалы. ИДП P9 строится на основе множеств качественных и сопряженных с ними числовых экспертных оценок результата сравнения пар значений ЧДП, возможно, с использованием задаваемых экспертом ОЧТ этих парных оценок [3]. До начала сравнения значений ЧДП значения ИДП {P7s=0, s=1, …, m}. После измерения значений {pxs} ЧДП {px} для обследуемых {os} значения ЧДП попарно сравниваются у обследуемых {(oi, ok), i=1, …, m–1; k=i+1, …, m}. Значения P7i и P7k ИДП P7 у oi и ok после сравнения pxi и pxk меняются по правилу P7i=P7i+wx, если pxi у oi лучше, чем pxk у ok, или pxi лучше, чем pxk, не менее, чем на dx>0 (d>0), значение P7k у ok в этом случае не меняется. Обозначим через Rк(pxi, pxk) результат парного экспертного сравнения величин pxi и pxk у oi и ok, измеренный в качественной шкале с множеством значений {хуже, равны, лучше}. Для снижения вопросной нагрузки на эксперта и потенциальной противоречивости формируемой системы парных оценок в методике и АС используется ОЧТ {Rк(pxi, pxs) & Rк(pxs, pxk)ÞRк(pxi, pxk), s=1, …, m, i≠k, i≠s, k≠s} парных оценок {Rк(pxi, pxs), Rк(pxs, pxk)} результатов сравнения значений ЧДП {px} для обследуемых {oi, ok, os, i≠k, i≠s, k≠s}. Перед обращением к эксперту с вопросом о значении Rк(pxi, pxk) автоматизированной системой анализируются пары оценок {(Rк(pxi, pxs), Rк(pxs, pxk)), s=1, …, m, i≠k, s≠i, s≠k} и при возможности значение Rк(pxi, pxk) автоматически формируется на основе ОЧТ, заданного правилами 1. Символ & в определении ОЧТ имеет смысл «и» и истолковывается как «значение Rк(pxi, pxs) и значение Rк(pxs, pxk)». Правила 1
Рассмотрим алгоритм нахождения значения бинарной оценки Rк(pxi, pxk) результата сравнения значений pxi и pxk ЧДП px для обследуемых oi, ok, реализованный в АС. 1. Экспертом задается ОЧТ между парами значений ЧДП, например, с помощью правил 1. 2. Анализируются все пары оценок вида {Rк(pxi, pxs), Rк(pxs, pxk), s=1, …, m, i≠k, i≠s, k≠s}. 3. Если ни одной пары (Rк(pxi, pxs), Rк(pxs, pxk)) оценок, для которых с помощью ОЧТ уже определен результат их композиции Rк(pxi, pxk), не найдено, результат Rк(pxi, pxk) запрашивается у эксперта, для чего переходим к шагу 4. Если найдена одна пара, переходим к шагу 7, если несколько пар – к шагу 8. 4. Экспертом явно задается искомое значение качественной оценки Rк(pxi, pxk). 5. Изучается возможная противоречивость экспертной оценки Rк(pxi, pxk) и ранее найденных оценок. Для этого последовательно анализируются все пары оценок вида {(Rк(pxi, pxk), Rк(pxk, pxs)), (Rк(pxs, pxi), Rк(pxi, pxk)), s=1, ..., m, i≠k, s≠i, s≠k} и с помощью заданного ОЧТ предпринимаются попытки программно вычислить значения оценок {Rк(pxi, pxs), s=1, ..., m, i≠s} и {Rк(pxs, pxk), s=1, ..., m, s≠k}. 6. Если хоть одна из найденных на шаге 5 оценок {Rк(pxi, pxs)} и {Rк(pxs, pxk)} противоречит ранее сформированной, эксперту предлагается вернуться к шагу 4 и задать для оценки Rк(pxi, pxk) другое значение. При отсутствии противоречий экспертная оценка Rк(pxi, pxk) принимается. На основании соотношений, заданных правилами 2, находят значение оценки Rк(pxk, pxi) и переходят к поиску значения следующей оценки. 7. Результат композиции (Rк(pxi, pxs), Rк(pxs, pxk)) оценок автоматически становится значением оценки Rк(pxi, pxk) без обращения к эксперту. Затем с помощью правил 2 вычисляется значение зеркальной оценки Rк(pxk, pxi). 8. Факт нахождения нескольких пар {(Rк(pxi, pxs), Rк(pxs, pxk))} оценок, порождающих в ОЧТ различные значения Rк(pxi, pxk), свидетельствует о наличии скрытых противоречий в формируемой системе парных оценок, поэтому эксперту предлагается явно определить результат сравнения важности Rк(pxi, pxk), выбрав наиболее подходящее из значений, найденных при помощи ОЧТ. Затем с помощью правил 2 вычисляется значение оценки Rк(pxk, pxi). Правила 2
Для снижения вопросной нагрузки на эксперта можно алгоритмически вычислять оценки Rк(pxi, pxk) и в тех случаях, когда на множествах значений {pxs} ЧДП {px} задано отношение порядка: " (pxi, pxk): pxi>pxkÞRк(pxi, pxk)=лучше (Rк(pxi, pxk)=хуже) или " (pxi, pxk): pxi При отсутствии априорных экспертных требований к значениям ЧДП в рамках методики используется также ИДП P8, учитывающий суммарное превышение значениями ЧДП у каждого из обследуемых аналогичных значений для остальных обследуемых при условии перевода значений всех ЧДП в единую измерительную шкалу. Для каждого ЧДП {px, x=1, …, n} сравниваются пары значений {(pxi, pxk)} у обследуемых {(oi, ok), i=1, …, m–1, k=i+1, …, m}. Значения P8i и P8k ИДП P8 для обследуемых oi и ok после сравнения величин pxi, pxk обрабатываются по правилам: P8i=P8i+|pxi–pxk|, если pxi›pxk (pxi›pxk и |pxi–pxk|>d). Если pxi‹pxk (pxi‹pxk и |pxi–pxk|>d), то P8k=P8k+|pxi–pxk|. Здесь |pxi – pxk| – модуль разности значений pxi и pxk, d>0 – порог различения отличий между значениями px. Для сравнения ПФС обследуемых при отсутствии априорных требований к значениям ЧДП также используется ИДП P9, вычисляемый путем сравнения пар значений ЧДП у обследуемых {(oi, ok), i=1, …, m–1, k=i+1, …, m} по формулам P9i=P9i+Rч(pxi, pxk), P9k=P9k+Rч(pxk, pxi), Rч(pxk, pxi)=mч max–Rч(pxi, pxk). При этом сопряженные качественное и числовое отношения Rк и Rч определяются экспертом на множествах пар значений ЧДП {(pxi, pxk), x=1, ..., n, i=1, ..., m, k=1, …, m} в виде Rк(pxi, pxk)® ®mкzÎМзнк и Rч(pxi, pxk)®mчzÎМзнч, где mкz, mчz – z-е элементы множеств Мзнк, Мзнч значений Rк и Rч. Отношение Rк(pxi, pxk) определяет результат качественного сравнения значений pxi и pxk, Rч(pxi, pxk) – его числовой аналог, mч max – максимальное значение Rч. Множество Mзнк по решению эксперта может включать элементы {«pxi лучше pxk», «pxi и pxk неразличимы», «pxi хуже pxk»}, {«pxi значительно лучше pxk (ЗЛ)», «pxi лучше pxk (ЛУ)», «pxi немного лучше pxk (НЛ)», «pxi и pxk равны (неразличимы) (РВ)», «pxi немного хуже pxk (НХ)», «pxi хуже pxk (ХЖ)», «pxi значительно хуже pxk (ЗХ)»} или иные, а Mзнч – элементы {1; 0,5; 0}, {1,002; 0,835; 0,668; 0,501; 0,334; 0,167; 0}, {0; 0,166; 0,332; 0,498; 0,664; 0,83; 0,996} или др. При этом mч max=1; 1,002; 0,996 или иному. Отношения Rк и Rч порождают сопряженные качественную и числовую измерительные шкалы [3]. Для снижения вопросной нагрузки на эксперта на множествах пар качественных {(Rк(pxi, pxs), Rк(pxs, pxk)), x=1, …, n, i=1, ..., m, s=1, ..., m, k=1, ..., m, i≠s, s≠k, i≠k} и сопряженных с ними числовых оценок {(Rч(pxi, pxs), Rч(pxs, pxk))} могут задаваться ОЧТ вида: Rк(pxi, pxs) & Rк(pxs, pxk)ÞRк(pxi, pxk), Rч(pxi, pxs) & Rч(pxs, pxk)ÞRч(pxi, pxk), в которых символом & обозначена композиция бинарных оценок Rк(pxi, pxs) и Rк(pxs, pxk), имеющая смысл «значение Rк(pxi, pxs) и значение Rк(pxs, pxk)». Анализ Rк и сущность стандартного отношения транзитивности позволяют описать ОЧТ между парами оценок значений ЧДП, измеренных в рассмотренной семизначной качественной шкале, например, с помощью правил 3. При другом сочетании значений {Rк(pxi, pxs), Rк(pxs, pxk), s=1, ..., m, i≠s, s≠k, i≠k} без участия эксперта значение оценки Rк(pxi, pxk) вычислить невозможно. ОЧТ может задаваться (описываться) и иным набором правил. Правила 3
Практика показывает, что использование таких ОЧТ позволяет значительно сократить объем диалога АС с экспертом, необходимого для формирования полного множества парных оценок {Rк(pxi, pxk)}, значительно снизить вероятность появления взаимно противоречивых оценок и повысить точность расчета КСЦ частных диагностических показателей. При этом формирование оценок {Rк(pxi, pxk)} результата сравнения значений {pxi}, {pxk} целесообразно проводить с помощью алгоритма, описанного ранее. Очевидно, для реализации вычислений в АС используется числовой аналог Rч заданного качественного ОЧТ Rк. Рассмотренные системы ИДП в целом соответствуют требованиям Всемирной организации здравоохранения, предъявляемым к интегральным показателям оценки здоровья человека. Остановимся на особенностях программной реализации описанной методики в разработанной АС. Программный модуль АС «Формирование оценок сравнительной важности пар частных диагностических показателей» позволяет пользователю задать, загрузить в программу и отредактировать сопряженные качественные и числовые измерительные шкалы [3], используемые для парного сравнения ценности ЧДП. Здесь же пользователь может задать ОЧТ для пар бинарных оценок. Программный модуль «Задание частных диагностических показателей и расчет весовых коэффициентов их важности» предоставляет пользователю возможность задать, загрузить в программу из файлов или отредактировать список исследуемых ЧДП, области их допустимых значений и провести парное экспертное сравнение ценности ЧДП с помощью заданной качественной измерительной шкалы и сформированного ОЧТ парных оценок, после чего на основе сопряженной числовой шкалы произвести расчет КСЦ частных показателей и сохранить их в специальных файлах. Перед началом работы данного и следующих модулей пользователь должен задать две опции – тип вычисляемых ИДП (с учетом или без учета требований к значениям ЧДП), а также форму ввода исходных данных – при помощи клавиатуры непосредственно в АС или путем импорта из заранее подготовленной таблицы MS Excel. В АС реализован поэтапный принцип решения диагностической задачи (реализации описанной методики) с возможностью его остановки и возобновления по желанию пользователя, а также возможностью на ряде этапов использовать те или иные ранее введенные данные, хранящиеся в ASCII-файлах с различными расширениями. Программные модули «Расчет интегральных диагностических показателей на основе весов частных показателей», «Расчет интегральных диагностических показателей с учетом разницы значений частных показателей» и «Расчет динамических интегральных диагностических показателей» вычисляют системы ИДП (1)–(4). При этом результаты измерения значений ЧДП для обследуемых в моменты t1 и t2 вводятся в программу с различных листов таблицы MS Excel. К плюсам методики и используемых в ней систем ИДП относится учет в них достоинств и недостатков ПФС обследуемых, а также баланса между ними, учет сравнительной ценности ЧДП, независимость ИДП от номенклатуры, особенностей ЧДП и их измерительных шкал, ясный содержательный смысл, хорошая интерпретируемость полученных результатов, простая структура и алгоритмы расчета, возможность использования для оценки ПФС обследуемых в фиксированный момент и во временной динамике, при наличии и отсутствии априорных экспертных требований к значениям ЧДП. Важной особенностью методики является отсутствие в ней вычислительных процедур и алгоритмов, понимание которых требует от пользователей – врачей, психологов, социологов – глубоких знаний в теории измерений, математической статистике, матричной алгебре, теории многокритериального принятия решений, что отличает методику от многих ИДП и вычислительных схем, описанных, например, в [1, 2]. Методика и разработанная на ее основе АС могут использоваться специалистами и должностными лицами как самостоятельно, так и вместе с другими методиками анализа медицинских, психологических и социологических данных для повышения обоснованности принимаемых решений. Литература 1. Толстова Ю.Н. Измерение в социологии: курс лекций. М.: ИНФРА, 1998. 224 с. 2. Экспертные оценки: методы и применение : обзор / Д.С. Шмерлинг [и др.] // Статистические методы анализа экспертных оценок. М.: Наука, 1977. С. 85–95. 3. Ермаков А.Е. Методика расчета коэффициентов сравнительной ценности диагностических показателей // Программные продукты и системы. 2010. № 4 (92). С. 177–183. 4. Ермаков А.Е., Найденова К.А., Григорьева Н.М. Использование интегральных показателей для оценки текущего психологического и физиологического состояния военнослужащих и его временной динамики // Военная профилактическая медицина. Проблемы и перспективы: матер. 1-го съезда воен. врачей медико-профилакт. профиля ВС РФ. СПб: ВМедА, 2002. С. 515–518. 5. Ермаков А.Е. Методика сравнительной оценки психического и физиологического состояния обследуемых с помощью систем интегральных показателей В кн.: Актуальные проблемы военной медицины: избран. тр. НИЦ академии // Вестн. РВМедА (приложение). 2009. № 3 (27). С. 60–67. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2779&like=1&page=article |
Версия для печати Выпуск в формате PDF (5.35Мб) Скачать обложку в формате PDF (1.27Мб) |
| Статья опубликована в выпуске журнала № 2 за 2011 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



 " pi: piÎQiдоп;
" pi: piÎQiдоп;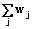 " pj: pjÎQjнед; (1)
" pj: pjÎQjнед; (1) " pi: piÎQiдоп;
" pi: piÎQiдоп;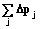 " pj: pjÎQjнед; (2)
" pj: pjÎQjнед; (2)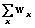 " px: pxi›pxs;
" px: pxi›pxs; " py: pyi‹pys; (3)
" py: pyi‹pys; (3) " px: pxi›pxs;
" px: pxi›pxs; " py: pyi‹pys; (4)
" py: pyi‹pys; (4)