При проектировании микросхем, используемых в космических летательных аппаратах, одной из основных задач является обеспечение стойкости к воздействию тяжелых заряженных частиц (ТЗЧ) космического пространства (КП). Для современных больших интегральных схем (БИС) с высокой степенью интеграции достаточно попадания одной такой частицы в чувствительный объем прибора, чтобы произошел сбой в его функционировании. Задача прогнозирования частоты возникновения одиночных сбоев и отказов, вызванных попаданием ТЗЧ КП, представляется достаточно сложной, поскольку реальная радиационная обстановка КП характеризуется весьма широким набором видов ТЗЧ и значений их энергии, а также наличием высокоэнергетических протонов, способных вызывать одиночные сбои различного характера. Кроме того, потоки протонов и ТЗЧ характеризуются изотропным угловым распределением.
Наиболее общий подход к прогнозированию чувствительности БИС к одиночным сбоям заключается в том, что вблизи элементарной ячейки БИС, подверженной сбоям, выделяется так называемый чувствительный объем (как правило, в виде прямоугольного параллелепипеда), в котором при поглощении энергии ТЗЧ, превышающей критическое значение Екрит, происходит сбой в работе прибора.
 При выборе физической модели для прогнозирования чувствительности к одиночным сбоям основное значение имеет определение доминирующих процессов сбора заряда из трека ТЗЧ в чувствительном объеме прибора. Обычно в качестве чувствительного объема выступает область пространственного заряда (ОПЗ) обратно смещенного p-n-перехода. Во многих работах отмечалось, что величина собранного заряда из трека при прямом попадании ТЗЧ в ОПЗ может значительно возрастать за счет эффекта воронки, когда реализуется дрейфовый механизм сбора заряда из трека ТЗЧ. Однако авторы многих работ (например [1, 2]) приходят к заключению, что диффузия является доминирующим процессом в сборе заряда из трека ТЗЧ: носители заряда, генерируемые вне ОПЗ, диффундируют к ее границе и вносят вклад в суммарный собранный заряд. В зависимости от того, на каком удалении от ОПЗ располагается ионный трек, при неизменном значении линейных потерь энергии (ЛПЭ) падающих ТЗЧ величина собранного заряда будет меняться. Это в конечном итоге приводит к тому, что зависимость сечения сбоев от ЛПЭ имеет вид плавно нарастающей функции, для аналитического описания которой часто используется аппроксимация распределением Вейбулла.
При выборе физической модели для прогнозирования чувствительности к одиночным сбоям основное значение имеет определение доминирующих процессов сбора заряда из трека ТЗЧ в чувствительном объеме прибора. Обычно в качестве чувствительного объема выступает область пространственного заряда (ОПЗ) обратно смещенного p-n-перехода. Во многих работах отмечалось, что величина собранного заряда из трека при прямом попадании ТЗЧ в ОПЗ может значительно возрастать за счет эффекта воронки, когда реализуется дрейфовый механизм сбора заряда из трека ТЗЧ. Однако авторы многих работ (например [1, 2]) приходят к заключению, что диффузия является доминирующим процессом в сборе заряда из трека ТЗЧ: носители заряда, генерируемые вне ОПЗ, диффундируют к ее границе и вносят вклад в суммарный собранный заряд. В зависимости от того, на каком удалении от ОПЗ располагается ионный трек, при неизменном значении линейных потерь энергии (ЛПЭ) падающих ТЗЧ величина собранного заряда будет меняться. Это в конечном итоге приводит к тому, что зависимость сечения сбоев от ЛПЭ имеет вид плавно нарастающей функции, для аналитического описания которой часто используется аппроксимация распределением Вейбулла.
Модель накопления заряда
Задачи моделирования сбора заряда из трека ТЗЧ являются принципиально трехмерными, и их решение представляется весьма сложным (в силу таких факторов, как сложность конструкции прибора, для которого проводится моделирование, случайность расположения трека ТЗЧ, изотропная геометрия облучения прибора в реальных условиях КП и др.). Как правило, задачи подобного рода решаются с применением специализированных САПР, и даже в этих случаях используются различные допущения и приближения, существенно упрощающие выполнение поставленной задачи.
В настоящей работе предлагается упрощенный метод моделирования процессов сбора заряда из трека ТЗЧ для прогнозирования характеристик чувствительности БИС к одиночным радиационным эффектам. Целью данных расчетов является определение порогового значения ЛПЭ ТЗЧ, при котором наблюдаются одиночные сбои. При этом моделирование проводится лишь для случая по- падания ТЗЧ непосредственно в центр чувствительной области, что будет соответствовать максимальному значению собранного заряда. Для достижения поставленной цели процесс моделирования сбора заряда предлагается свести к решению упрощенной задачи, основанной на следующих предположениях.
Во-первых, чувствительный объем представляется в виде цилиндра, по оси которого проходит трек ТЗЧ (рис. 1). Вдоль оси цилиндра направлена координатная ось z. Заряд, генерированный в треке, собирается коллекторной областью (z=0), которой является верхняя торцевая поверхность цилиндра. В начальный момент задается радиальное распределение носителей заряда в треке, а дальше рассматривается эволюция трека с учетом объемной рекомбинации носителей заряда.
Во-вторых, предполагается отсутствие внешнего поля. Таким образом, рассматривается только заряд, собранный посредством диффузии. В работах [1, 3] отмечается, что учет вклада дрейфа носителей в суммарную величину собранного заряда может быть проведен путем удвоения диффузионного тока. При этом следует понимать: такое приближение не означает, что временная форма импульса дрейфовой составляющей ионизационного тока совпадает с формой диффузионной составляющей. Приближение позволяет лишь оценить конечный результат – заряд, собранный за счет диффузии и дрейфа неравновесных носителей.
В-третьих, объемная рекомбинация определяется двумя механизмами: Оже-рекомбиницией (характерно для высокого уровня инжекции) и рекомбинацией Шокли–Рида–Холла (характерно для низкого уровня инжекции). Общая скорость объемной рекомбинации Rrec будет складываться из скоростей этих двух видов рекомбинации:
Rrec=RAuger+RSRH. (1)
Для скорости Оже-рекомбинации RAuger можно записать:
 (2)
(2)
где n и р – полные концентрации носителей; n0 и р0 – начальные равновесные концентрации носителей [2].
Значения Оже-коэффициентов Ce и Сh для кремния обычно составляют порядка 2×10–31 см6/с.
Для скорости рекомбинации Шокли–Рида–Холла можно записать:
 , (3)
, (3)
где  – время жизни электронов и дырок (при низком уровне инжекции); vthn, vthp – тепловая скорость электронов и дырок соответственно; sn, sp – сечение захвата электронов и дырок соответственно [2].
– время жизни электронов и дырок (при низком уровне инжекции); vthn, vthp – тепловая скорость электронов и дырок соответственно; sn, sp – сечение захвата электронов и дырок соответственно [2].
Для низкого уровня инжекции (когда доминирует механизм рекомбинации Шокли–Рида–Холла) можно приблизительно считать, что скорость рекомбинации определяется выражением
 , (4)
, (4)
где tpl=tnl=t.
Следует отметить, что в состоянии с высоким уровнем инжекции, что типично для ионных треков, перенос неравновесных электронов и дырок осуществляется за счет амбиполярной диффузии, коэффициент которой может быть рассчитан по формуле
 , (5)
, (5)
где Dmin, Dmaj – коэффициенты диффузии неосновных и основных носителей заряда [1, 2]. В состоянии с низким уровнем инжекции диффузионный перенос неравновесных носителей заряда определяется их коэффициентами диффузии.
В-четвертых, предполагается наличие аксиальной симметрии относительно оси z (направление начального трека). Если использовать цилиндрическую систему координат, данное предположение позволяет превратить решаемую задачу из трехмерной в двухмерную относительно независимых координат z и r. Плотность носителей заряда не будет зависеть от полярного угла из-за наличия аксиальной симметрии относительно оси z.
Общий ток, характеризующий значение собранного заряда, определяется диффузионным током неосновных носителей заряда. Как уже отмечалось, учет вклада дрейфовой составляющей в величину собранного заряда может осуществляться путем удвоения диффузионного тока [1, 3].
Известно [2], что обычно в качестве чувствительной области, отвечающей за возникновение одиночных обратимых сбоев при воздействии ТЗЧ, выступает ОПЗ стокового p-n-перехода закрытого n-канального транзистора. Если считать, что уровень легирования n+-стоковой области значительно выше, чем в р-подложке, то ОПЗ будет практически полностью сосредоточена в подложке. Следовательно, как неосновные носители заряда можно рассматривать электроны. В качестве границы между высоким и низким уровнями инжекции можно взять равенство концентраций избыточных неосновных носителей (электронов) и основных носителей заряда (дырок): n–n0=p0. Если концентрация избыточных электронов превышает равновесную концентрацию дырок, то реализуется состояние с высоким уровнем инжекции, иначе – с низким.
Радиус области сбора заряда R выбирается исходя из значения площади чувствительной области SЧО:
 . (6)
. (6)
В случае одиночных обратимых сбоев чувствительными областями являются стоковые переходы закрытых n-канальных транзисторов, и их площадь определяется исходя из известных топологических размеров ячеек памяти. При отсутствии информации о топологии ячеек памяти можно ориентироваться на значение топологической нормы проектирования, характерное для технологии изготовления рассматриваемых БИС, и использовать эмпирическое соотношение для микросхем статических оперативных запоминающих устройств (СОЗУ):
SЗЯ[мкм2]»300(lT [мкм])2, (7)
где SЗЯ – площадь запоминающей ячейки; lT – топологическая норма проектирования [2].
В этом случае площадь чувствительной области может быть оценена как половина площади одного транзистора, то есть 1/12 площади 6-транзисторной ячейки памяти СОЗУ.
Следует отметить, что площадь чувствительной области соответствует значению сечения насыщения для обратимых сбоев, которое вместе с пороговыми ЛПЭ является основным параметром чувствительности БИС к сбоям при воздействии ТЗЧ, необходимым для расчета частоты сбоев.
Глубина области сбора заряда Z0 определяется глубиной залегания стоковых p-n-переходов, шириной ОПЗ этих переходов и длиной воронки. В большинстве случаев эта величина составляет порядка 3 мкм.
С учетом рассмотренных предположений моделирование сбора заряда из трека ТЗЧ в случае нормального падения ТЗЧ по центру области сбора заряда может быть проведено следующим образом.
1. Решается краевая задача для распределений концентрации носителей заряда в чувствительном объеме, которая с учетом рассмотренных допущений формулируется в виде
 (8)
(8)
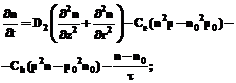 (9)
(9)
 ;
;  ; (10)
; (10)
 ; (11)
; (11)
 (12)
(12)
 (13)
(13)
 (14)
(14)
Данная задача решается для различных значений ЛПЭ падающих частиц, которые определяют начальную концентрацию электронно-дырочных пар в треке.
2. Вычисляется диффузионный ток неосновных носителей заряда (электронов) через верхнюю торцевую поверхность цилиндрического чувствительного объема:
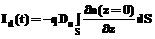 . (15)
. (15)
В полярной системе координат с учетом аксиальной симметрии относительно оси z выражение (15) можно преобразовать следующим образом:

 . (16)
. (16)
3. Рассчитывается собранный заряд путем интегрирования выражения (16), при этом для учета вклада дрейфовой компоненты в величину собранного заряда значение диффузионного тока удваивается:
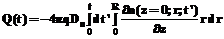 . (17)
. (17)
Моделирование воздействия ТЗЧ на микросхемы и оценка их адекватности
На основе полученной модели было разработано ПО, на которое выдано свидетельство о регистрации программ № 2102611565 от 17.02.2011 (авторы: Затворницкий А.П., Таперо К.И., Зольников В.К.). Результаты величины тока ионизации включены в программы схемотехнического моделирования в виде динамических генераторов тока. При этом МОП-транзисторные элементы рассматривались как совокупность МОП-транзистора и паразитного биполярного. Основными процессами, происходящими в МОП-транзисторе при воздействии одиночных ядерных частиц, являются возникновение импульсов ионизационных токов в p-n-переходе «Сток – Подложка», вследствие чего происходят кратковременное увеличение тока стока и уменьшение порогового напряжения МОП-транзистора, что вызывает переключение логического состояния на выходе логических элементов.
Использование предложенной эквивалентной электрической схемы приводит к увеличению активных элементов в СБИС. Однако эти элементы будут учитываться только у тех транзисторов, которые на первом этапе (анализ топологических размеров элементов и определение величины порогового заряда) попали в разряд проблемных (то есть таких, у которых локальные эффекты будут происходить с наибольшей вероятностью). Это соответствует общему подходу, так как при оценке стойкости любого изделия к радиации используется наихудший случай.
Результаты моделирования позволили оценить зависимость величины сечения взаимодействия от ЛПЭ. Определено пороговое значение ЛПЭ тяжелых заряженных частиц для одиночных обратимых сбоев. В качестве порогового выбирается такое значение ЛПЭ, при котором собранный заряд равен заряду переключения логического состояния КМОП-триггера, для которого проводится моделирование. Величина заряда переключения обычно известна: как правило, она рассчитывается на этапе разработки конструкции и технологии СБИС.
Для оценки точности моделирования проведены экспериментальные исследования. В качестве объекта испытаний выбран 16-разрядный микроконтроллер с системой команд 1874ВЕ36, ОЗУ – 488×8 и адресуемой памятью 64К×8, предназначенный для применения в аппаратуре и эксплуатирующийся в условиях воздействия внешних специальных факторов.
В ходе испытаний на воздействие ТЗЧ определяются пороговая величина уровня линейной потери энергии для одиночных обратимых сбоев от воздействия ТЗЧ и время потери работоспособности. Параметры (критерии работоспособности) – UOL, UOH, IОСC1, IОСC2, функциональный контроль по заданному алгоритму.
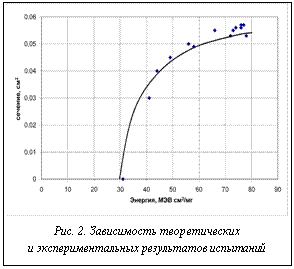
Результаты испытаний можно представить зависимостью, показанной на рисунке 2. На нем изображены теоретическая кривая и экспериментальные точки. Пороговое значение ЛПЭ для одиночных обратимых сбоев составляет 30 МЭВ см2/мг. Время потери работоспособности не превышает 2 мс.
Как показывает сравнение экспериментальных и теоретических результатов, они хорошо согласуются.
В заключение отметим, что предлагаемая методика позволяет рассчитать для заданного значения ЛПЭ падающих частиц форму импульса диффузионной составляющей ионизационного тока и за- висимость собранного заряда от времени после попадания частицы. По получении зависимости собранного заряда от значения ЛПЭ ТЗЧ может быть определено пороговое значение ЛПЭ ТЗЧ для одиночных обратимых сбоев. В качестве порогового выбирается такое значение ЛПЭ, при котором собранный заряд равен заряду переключения логического состояния КМОП-триггера, для которого проводится моделирование. Величина заряда пе- реключения обычно известна: как правило, она рассчитывается на этапе разработки конструкции и технологии БИС.
 Результатом реализации предлагаемого метода будет оценка порогового значения ЛПЭ ТЗЧ и сечения насыщения для одиночных сбоев. Полученное пороговое значение ЛПЭ соответствует случаю нормального падения ТЗЧ на кристалл БИС. Аналогичные характеристики, как правило, получаются и в экспериментах на ускорителях тяжелых ионов. Для восстановления зависимости сечения сбоев от ЛПЭ можно применить аппроксимацию распределением Вейбулла с использованием полученных значений пороговых ЛПЭ и сечения насыщения, а для определения значений оставшихся параметров аппроксимации воспользоваться рекомендациями из [4].
Результатом реализации предлагаемого метода будет оценка порогового значения ЛПЭ ТЗЧ и сечения насыщения для одиночных сбоев. Полученное пороговое значение ЛПЭ соответствует случаю нормального падения ТЗЧ на кристалл БИС. Аналогичные характеристики, как правило, получаются и в экспериментах на ускорителях тяжелых ионов. Для восстановления зависимости сечения сбоев от ЛПЭ можно применить аппроксимацию распределением Вейбулла с использованием полученных значений пороговых ЛПЭ и сечения насыщения, а для определения значений оставшихся параметров аппроксимации воспользоваться рекомендациями из [4].
Основным преимуществом предлагаемого метода прогнозирования характеристик чувствительности БИС к одиночным сбоям при воздействии ТЗЧ является то, что оценка этих характеристик получается практически на основе рассмотрения только диффузионных механизмов переноса заряда. Реальный учет дрейфовой компоненты в уравнениях непрерывности для неравновесных носителей заряда представляется весьма сложным, поскольку современные БИС имеют очень непростую конструкцию, включающую большое количество контактов, p-n-переходов, границ раздела и т.п., и в процессе воздействия ТЗЧ микросхемы могут находиться в динамическом режиме. В результате точное описание распределения электрического потенциала по объему кристалла БИС представляет собой очень трудную задачу.
На основе данного материала можно провести моделирование стойкости к воздействию ТЗЧ всех основных элементов микросхем, выявить наиболее критичные и с помощью специальных мер повысить стойкость изделий.
Литература
1. Edmonds L.D. A Time-Dependent Charge-Collection Efficiency for Diffusion // IEEE Trans. Nucl. Sci. 2001, Vol. 48, № 5, pp. 1609–1622.
2. Weatherford T. From Carriers to Contacts, a Review of SEE Charge Collection Processes // Radiation Effects – From Particles to Payloads. IEEE NSREC Short Course, 2002, Sec. IV, pp. 1–80.
3. Edmonds L.D. Electric Currents through Ion Tracks in Silicon Devices // IEEE Trans. Nucl. Sci. 1998, Vol. 45, № 6, pp. 3153–3164.
4. ГОСТ 25645.150–90. Лучи космические галактические. Модель изменения потоков частиц. Госкомитет СССР по стандартам, 1991.




 (2)
(2) , (3)
, (3) – время жизни электронов и дырок (при низком уровне инжекции); vthn, vthp – тепловая скорость электронов и дырок соответственно; sn, sp – сечение захвата электронов и дырок соответственно [2].
– время жизни электронов и дырок (при низком уровне инжекции); vthn, vthp – тепловая скорость электронов и дырок соответственно; sn, sp – сечение захвата электронов и дырок соответственно [2]. , (4)
, (4) , (5)
, (5) . (6)
. (6) (8)
(8)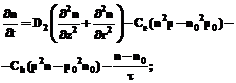 (9)
(9) ;
;  ; (10)
; (10) ; (11)
; (11) (12)
(12) (13)
(13) (14)
(14)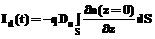 . (15)
. (15)
 . (16)
. (16)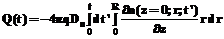 . (17)
. (17) Результатом реализации предлагаемого метода будет оценка порогового значения ЛПЭ ТЗЧ и сечения насыщения для одиночных сбоев. Полученное пороговое значение ЛПЭ соответствует случаю нормального падения ТЗЧ на кристалл БИС. Аналогичные характеристики, как правило, получаются и в экспериментах на ускорителях тяжелых ионов. Для восстановления зависимости сечения сбоев от ЛПЭ можно применить аппроксимацию распределением Вейбулла с использованием полученных значений пороговых ЛПЭ и сечения насыщения, а для определения значений оставшихся параметров аппроксимации воспользоваться рекомендациями из [4].
Результатом реализации предлагаемого метода будет оценка порогового значения ЛПЭ ТЗЧ и сечения насыщения для одиночных сбоев. Полученное пороговое значение ЛПЭ соответствует случаю нормального падения ТЗЧ на кристалл БИС. Аналогичные характеристики, как правило, получаются и в экспериментах на ускорителях тяжелых ионов. Для восстановления зависимости сечения сбоев от ЛПЭ можно применить аппроксимацию распределением Вейбулла с использованием полученных значений пороговых ЛПЭ и сечения насыщения, а для определения значений оставшихся параметров аппроксимации воспользоваться рекомендациями из [4].