Для поддержки принятия решений в различных информационных системах, например, бизнес-приложениях, системах документооборота, системах электронного обучения с высокой степенью адаптивности и т.д., используется прогнозирование. Его частными случаями являются задачи классификации данных и восстановления регрессии. Основное отличие между ними в том, что в первом случае результат прогноза принадлежит множеству непересекающихся классов, а во втором представляет собой вещественное число. Так или иначе, в обоих случаях для успешного прогнозирования должно быть выполнено обучение системы с использованием тестовой выборки данных.
В данной статье предлагается эффективный алгоритм классификации данных с использованием деревьев решений и генетических алгоритмов.
Деревья решений – это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение. На ребрах дерева записываются атрибуты, от которых зависит целевая функция, в листьях – значения целевой функции, а в остальных узлах – атрибуты, по которым различаются случаи.
Основная идея построения деревьев решений из некоторого обучающего множества Х, сформулированная в интерпретации Р. Куинлена [1], состоит в следующем.
Пусть в некотором узле дерева сконцентрировано множество примеров Х*, Х*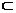 Х. В этом случае возможны три ситуации.
Х. В этом случае возможны три ситуации.
1. Множество Х* содержит один или более примеров, относящихся к одному классу yk. Тогда дерево решений для Х* – лист, определяющий класс yk.
2. Множество Х* не содержит ни одного примера, то есть является пустым множеством. Тогда это снова лист, и класс, ассоциированный с листом, выбирается из другого множества, отличного от Х* (скажем, из множества, ассоциированного с родителем).
3. Множество Х* содержит примеры, относящиеся к разным классам. В таком случае множество Х* следует разбить на некоторые подмножества. Для этого выбирается один из признаков j, имеющий два и более отличных друг от друга значений, и Х* разбивается на новые подмножества, каждое из которых содержит все примеры, имеющие определенный диапазон значений выбранного признака. Процедура рекурсивно продолжится до тех пор, пока любое подмножество Х* не будет состоять из примеров, относящихся к одному и тому же классу.
В общем виде эвристический алгоритм построения дерева решений будет следующим.
1. Выбор критерия разделения с целью поиска наиболее подходящего атрибута для проверки в каждом узле дерева.
2. Разделение выборки на две или более частей в соответствии со значениями атрибута, выбранного на основании критерия разделения.
3. Рекурсия начиная с шага 2. Образовавшиеся подмножества разделяются на более мелкие подмножества в соответствии с выбранным критерием до тех пор, пока в каждом из них не останутся объекты одного класса либо атрибуты, позволяющие эти объекты различить.
Данные шаги являются общими для большинства существующих алгоритмов построения дерева решений. Эти алгоритмы отличаются друг от друга выбором критерия разделения, а также механизмом отсечения узлов дерева и другими параметрами.
В некоторых методах для выбора атрибута расщепления используется так называемая мера информативности подпространств атрибутов, которая основывается на энтропийном подходе и известна под названием «мера информационного выигрыша» (information gain measure), или «мера энтропии». Подобный подход применен в таких алгоритмах, как ID3 и C4.5. В соответствии с этим критерием лучшим для разделения считается признак, дающий максимальную информацию о классах. Эта величина определяется по формуле количества информации:
 , (1)
, (1)
где H(Y) – энтропия множества Y; H(Y|X) – средняя условная энтропия множества Y при известном множестве X. Величины H(Y) и H(Y|X) определяются по формулам:
 , (2)
, (2)
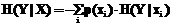 , (3)
, (3)
где p(xi) и p(yi) – вероятности выбора того или иного значения из множеств X и Y соответственно; H(Y|xi) – условная энтропия, если известно, что из X выбрано значение xi. Условная энтропия определяется по формуле
 . (4)
. (4)
При разделении выборки всегда выбирается атрибут, дающий максимальный выигрыш информации для целевого атрибута, то есть для которого значение Gain(Y|X) является максимальным среди всех X. Здесь X – множество значений атрибута классифицируемых объектов, Y – множество значений целевого атрибута.
Приведенные формулы позволяют вычислять количество информации для атрибутов, представляющих дискретные (а точнее, номинальные) значения. На практике часто встречаются целочисленные и даже вещественные атрибуты. Наиболее приемлемым было бы трактовать любой атрибут как номинальный и подсчитывать относительные частоты (как оценки вероятностей) для каждого встреченного значения, однако подобный подход приведет к неконтролируемому разрастанию дерева и потере его обобщающей способности. Одним из решений данной проблемы является использование так называемой пороговой энтропии, которая определяется по формуле
 (5)
(5)
Тогда формула количества информации примет вид
 . (6)
. (6)
Таким образом, можно использовать слегка видоизмененный критерий количества информации применительно к любым атрибутам, для которых имеет смысл операция сравнения, в частности, для вещественных и целочисленных.
С критерием количества информации связана одна существенная проблема: алгоритм зачастую выбирает атрибуты, имеющие наибольшее количество различных значений. Например, если один из атрибутов в выборке данных обозначает дату какого-либо свершившегося события, то вполне вероятно, что именно этот атрибут будет выбран для разделения. В таком случае полученное дерево решений окажется совершенно бесполезным, поскольку уже прошедшие даты никогда не повторятся.
Другой критерий расщепления, предложенный Л. Брейманом и др. [2], реализован в алгоритме CART и называется индексом Gini. При помощи этого индекса атрибут выбирается на основании расстояний между распределениями классов:
 , (7)
, (7)
где pi – вероятность (относительная частота) класса i в выборке T.
Помимо перечисленных критериев, иногда эффективен выбор атрибута по количеству различных значений в выборке. Разделение по атрибуту, содержащему максимальное количество значений в выборке, зачастую оказывается эффективным для числовых атрибутов. В этом случае в качестве значения разделения можно использовать математическое ожидание множества X. Разделение по атрибуту, содержащему минимальное количество значений в выборке, тоже бывает эффективнее предложенных критериев, особенно если речь идет о дискретных (номинальных) атрибутах. Значение разделения в таком случае тоже можно выбрать исходя из распределения значений в выборке.
Несмотря на широкое применение, эвристические методы построения деревьев решений принципиально не способны находить наиболее полные и точные правила классификации данных, поскольку они основаны на использовании жадных алгоритмов. Если один раз был выбран атрибут и по нему произведено разбиение на подмножества, алгоритм не может вернуться и выбрать другой атрибут, который дал бы лучшее разбиение. Поэтому на этапе построения нельзя сказать, даст ли выбранный атрибут оптимальное разбиение в конечном итоге.
Другой существенный недостаток эвристических алгоритмов в том, что при разделении выборки используется один и тот же критерий, а это зачастую приводит к неверному выбору атрибута и значения разделения.
Существенное повышение точности классификации возможно, если процесс построения дерева решений трансформировать в задачу поиска и использования оптимальной последовательности локальных целевых функций (другими словами, оптимальной последовательности эвристик), применяемых в подзадачах разделения выборки данных. При этом подразумевается, что трансформированная задача будет решаться эволюционными методами. В частности, в данной работе рассматривается применение генетического алгоритма.
Подобный подход уже был успешно применен к задачам синтеза расписаний и назван методом комбинирования эвристик (НСМ – Heuristics Combination Method) [3]. Данная статья иллюстрирует возможности и особенности применения НСМ для оптимального подбора эвристик при построении дерева решений.
В генетических методах любое решение задачи синтеза представляется хромосомой, состоящей из генов. Аллелями являются значения проектных параметров [4].
 Главная особенность HCM в том, что аллелями служат не значения проектных параметров, а имена эвристик, используемых для определения этих значений. Выполнение условий допустимости переносится в сами эвристики, что делает генетический алгоритм инвариантным к различным задачам. Другими словами, в НСМ i-й ген соответствует i-й подзадаче, а i-я аллель есть номер (имя) процедуры (эвристики), реализующей локальную целевую функцию и ограничения i-й подзадачи. В НСМ для каждой подзадачи должно быть сформулировано несколько альтернативных постановок (процедур) – именно из них генетический алгоритм и будет выбирать членов последовательности, приближаясь к оптимальной последовательности эвристик.
Главная особенность HCM в том, что аллелями служат не значения проектных параметров, а имена эвристик, используемых для определения этих значений. Выполнение условий допустимости переносится в сами эвристики, что делает генетический алгоритм инвариантным к различным задачам. Другими словами, в НСМ i-й ген соответствует i-й подзадаче, а i-я аллель есть номер (имя) процедуры (эвристики), реализующей локальную целевую функцию и ограничения i-й подзадачи. В НСМ для каждой подзадачи должно быть сформулировано несколько альтернативных постановок (процедур) – именно из них генетический алгоритм и будет выбирать членов последовательности, приближаясь к оптимальной последовательности эвристик.
В соответствии с предлагаемым алгоритмом в каждой подзадаче исходной задачи, связанной с разделением выборки, выбирается критерий разделения по одной из следующих эвристик:
S1: выбирается атрибут, обладающий наибольшим значением индекса Gain(Y|X);
S2: выбирается атрибут с наибольшим значением индекса Gini(Y);
S3: выбирается атрибут, содержащий наибольшее количество значений в выборке данных;
S4: выбирается атрибут с наименьшим количеством значений в выборке данных;
S5: разделение выборки не производится (узел превращается в лист).
Хромосома в таком случае имеет древовидную структуру. Количество генов в ней совпадает с количеством узлов дерева, их значениями могут быть номера эвристик в диапазоне [1, 5].
Необычная структура хромосомы влияет на реализацию генетического алгоритма. Этап эволюции в данном случае заключается в выборе наиболее подходящей эвристики для соответствующего узла дерева. При этом используются особи с различными эвристиками в дочерних узлах. Далее выборка расщепляется в зависимости от выбранной эвристики и выполняется новый этап эволюции для подчиненных узлов (рис. 1). Новая популяция формируется из дочерних узлов дерева, что сокращает размер как хромосомы, так и выборки данных.
Чтобы обеспечить достаточное разнообразие особей, при формировании начальной популяции строятся деревья решений для каждой из эвристик в диапазоне [S1:S4]. При этом используются различные эвристики в дочерних узлах. Таким образом, размер начальной популяции составляет 16 особей (4 вида эвристики для корня дерева комбинируются с 4 видами эвристики для его дочерних узлов).
Оператор кроссовера для древовидных хромосом выполняется для определенного подмножества данных, соответствующего заданному узлу дерева, и состоит из следующих этапов.
1. Выбираются две хромосомы с одинаковыми генами, соответствующими корневому узлу дерева рассматриваемого подмножества данных.
2. В каждой из родительских хромосом меняются местами значения генов, соответствующих первому и второму подчиненным узлам дерева.
 Рисунок 2 иллюстрирует пример скрещивания двух хромосом для узла с эвристикой S2. Потомки образуются путем замены дочерних узлов левого и правого родителей.
Рисунок 2 иллюстрирует пример скрещивания двух хромосом для узла с эвристикой S2. Потомки образуются путем замены дочерних узлов левого и правого родителей.
Одно из главных ограничений рассмотренного оператора кроссовера – необходимость совпадения эвристик для рассматриваемого узла дерева. Не менее важное условие – количество дочерних узлов. Согласно алгоритму, местами меняются только два первых дочерних узла в родительских хромосомах. Остальные остаются неизменными.
Мутация хромосом представляет собой случайное изменение эвристики для рассматриваемого узла дерева. Поскольку основное назначение мутации – обеспечение разнообразия популяции, изменению может подвергаться любая из хромосом при условии, что в популяции есть аналогичная ей. Оптимальное количество особей для выполнения мутации k рассчитывается исходя из разнообразия популяции и количества особей в ней:
 , (8)
, (8)
где l – количество пар одинаковых хромосом; n – размер популяции.
Как видно из формулы (8), количество особей для мутации не должно превышать 25 % от общего размера популяции. В противном случае это может нарушить сходимость генетического алгоритма и привести к потере локального экстремума целевой функции f.
Алгоритм мутации состоит из следующих этапов.
1. Поиск в популяции пары хромосом с одинаковым значением эвристик во всех дочерних узлах.
2. Выбор из пары одной хромосомы (случайным образом) для проведения мутации.
3. Замена эвристики в корневом узле выбранной хромосомы (новый вид эвристики также выбирается случайным образом).
4. Если количество особей для мутации меньше k и в популяции остались одинаковые хромосомы – возврат к шагу 1.
В процессе отбора особей используется стратегия элитизма. При этом размер популяции остается неизменным, то есть из промежуточной популяции отбираются 16 особей, обладающих наибольшей точностью классификации.
Работа алгоритма останавливается после выполнения всех этапов эволюции (для каждого узла дерева, за исключением листьев). Дополнительно может быть введено ограничение на максимальное количество формируемых поколений (глубину дерева для поиска эвристик).
Для проверки алгоритма использовалась обучающая выборка из 3212 строк, содержащая информацию об исполнительской дисциплине сотрудников, собранную на основе данных документооборота организации. Элементы множества объектов X включают в себя следующие атрибуты.
1. Вид контроля – может принимать одно из двух значений: «Контроль за отделом» или «Контроль за исполнителем».
2. Исполнитель – содержит название отдела или Ф.И.О. исполнителя, которому назначена резолюция по документу.
3. Месяц, в который исполнителю был передан документ (число в интервале [1, 12]).
4. День недели, в который исполнителю был передан документ (число в интервале [1, 7]).
Множество ответов Y (целевой атрибут выборки) – это информация о нарушении срока исполнения резолюции (в днях). Для повышения точности классификации (снижения частоты ошибок) значения множества Y представлены не числом, а интервалом чисел, что позволяет отнести к одному и тому же классу разные значения целевого атрибута.
Результат выполнения алгоритма представлен в таблице. Для удобства восприятия частота ошибок выражена в процентах. Как видно, предложенный генетический алгоритм демонстрирует более высокую точность классификации данных в отличие от любого из эвристических алгоритмов.
Результаты классификации для выборки из 3212 строк
|
Алгоритм классификации
|
Частота ошибок, %
|
|
Критерий Gain
|
24,12
|
|
Критерий Gini
|
25,01
|
|
Разделение по максимальному количеству значений
|
26,53
|
|
Разделение по минимальному количеству значений
|
25,36
|
|
Алгоритм, встроенный в программу 1С:Предприятие
|
24,84
|
|
Генетический алгоритм
|
19,46
|
На рисунке 3 изображен график зависимости времени построения дерева решений от размера выборки. Благодаря сокращению размера выборки при переходе на новый этап эволюции, а также оптимизации вычисления критериев разделения данных, общее время выполнения алгоритма в среднем линейно зависит от размера обучающей выборки.
 Из таблицы и графика следует, что предложенный эволюционный алгоритм построения дерева решений показал лучшие по сравнению с другими моделями результаты при краткосрочном прогнозе. Применение эволюционных методов позволяет устранить недостаток эвристических алгоритмов, связанный с неправильным выбором критерия разделения при построении дерева решения, что, в свою очередь, повышает точность классификации данных и качество прогнозирования в целом.
Из таблицы и графика следует, что предложенный эволюционный алгоритм построения дерева решений показал лучшие по сравнению с другими моделями результаты при краткосрочном прогнозе. Применение эволюционных методов позволяет устранить недостаток эвристических алгоритмов, связанный с неправильным выбором критерия разделения при построении дерева решения, что, в свою очередь, повышает точность классификации данных и качество прогнозирования в целом.
Литература
1. Ross J. Quinlan. C4.5: Programs for Machine learning. Morgan Kaufmann Publishers, 1993.
2. Breiman L., Friedman J.H., Olshen R.A. and Stone C.T. Classification and Regression Trees. Wadsworth, Belmont, California, 1984.
3. Норенков И.П. Генетические методы структурного синтеза проектных решений // Информационные технологии. 1998. № 1. С. 9–13.
4. Goldberg D. Genetic Algorithms in Search, Optimization, and Machine Learning // Adison-Wesley Publ., 1989.

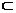 Х. В этом случае возможны три ситуации.
Х. В этом случае возможны три ситуации. , (1)
, (1) , (2)
, (2)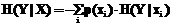 , (3)
, (3) . (4)
. (4) (5)
(5) . (6)
. (6) , (7)
, (7)

 , (8)
, (8)