Авторитетность издания
Добавить в закладки
Следующий номер на сайте
SLIPH4M – программа для численного решения проблемы Штурма–Лиувилля
Аннотация:Представлена программа, написанная на языке системы компьютерной алгебры MAPLE и предназначенная для вычисления спектра собственных значений и соответствующих собственных функций разностной задачи Штурма–Лиувилля. В ней реализованы итерационные схемы на основе непрерывного аналога метода Ньютона точности порядка O(h4), где h – шаг разностной сетки.
Abstract:A program written in the language of the computer algebra system MAPLE is presented to calculate the spectrum of eigenvalues and corresponding eigenfunctions of Sturm–Liouville differential equations. In the program the iteration schemes are realized on the base of a continuous analog of Newton’s method with accuracy O(h4), where h is the step size of the uniform grid.
| Авторы: Во Чонг Тхак (votrongthach@jinr.ru) - Объединенный институт ядерных исследований, г. Дубна, Пузынина Т.П. (puzynina@jinr.ru) - Объединенный институт ядерных исследований, г. Дубна, доктор физико-математических наук | |
| Ключевые слова: непрерывный аналог метода ньютона, задача штурма–лиувилля, собственная функция, собственное значение |
|
| Keywords: continuous analog of Newton’s method, Sturm–Liouville problem, eigenfunction, eigenvalue |
|
| Количество просмотров: 11382 |
Версия для печати Выпуск в формате PDF (5.05Мб) Скачать обложку в формате PDF (1.39Мб) |
При изучении математических моделей колебательных процессов, устойчивости систем, а также в квантовой механике часто возникает задача Штурма–Лиувилля (Ш–Л) на конечном и на бесконечном интервалах. Особое место в ее постановке занимают такие задачи, в которых коэффициенты уравнения представлены в виде таблиц, полученных из экспериментальных данных или из некоторых предварительных расчетов. Для более точного использования этих числовых данных целесообразно применять дискретные аппроксимации исходных задач. Одной из таких аппроксимаций, для которой приближенная задача Ш–Л исследована полностью, является метод конечных разностей [1]. Включение пакета решения задачи Ш–Л в этой постановке в программную среду MAPLE позволяет, с одной стороны, восполнить его отсутствие в этой среде, а с другой – обогатить пользовательский интерфейс пакета современ- ными средствами компьютерной аналитики и графики. Представляемый пакет программ SLIPH4М для решения разностной задачи Ш–Л использует итерационные схемы на основе непрерывного аналога метода Ньютона (НАМН) [2], эффективность которого проверена при решении ряда математических моделей из различных разделов физики, в том числе спектральных задач. В программе реализованы модификации ньютоновских итерационных схем, позволяющие решать указанную задачу с использованием априорной численной и аналитической информации, а возможности графической визуализации промежуточных и окончательных результатов делают более оперативным их анализ. Кроме того, вычисление с помощью пакета SLIPH4М собственных значений дает возможность при обращении к процедуре dsolve в системе MAPLE получить собственные функции в аналитическом виде. Созданный пакет программ является продолжением и развитием комплексов программ SLIPM [3] и SLIPH4 [4]. Рассмотрим постановку задачи. Для использования НАМН проблема Ш–Л записывается в виде системы функциональных уравнений j(z)=0, z=(l, y), j={j(j)}, j=1, 2, 3, 4 (1) для линейного дифференциального оператора второго порядка: j(1)(l, y)ºy¢¢(x)+2p(x)y¢(x)+(q(x)–lr(x))y(x)=0, a£x£b, (2) краевых условий общего вида:
и условия нормировки:
Здесь коэффициенты p(x), q(x), r(x) – заданные функции, обеспечивающие существование нетривиальных собственных решений y=yn(x) с указанными граничными условиями, которым соответствуют собственные значения параметра l=ln. Функции dj, fj (j=1, 2) непрерывно дифференцируемы по l и Граничные условия (3), (4) и условие нормировки (5) дают возможность учитывать асимптотики собственных функций тех задач, которые рассматриваются на полубесконечном интервале [a, ¥). Здесь y(l, x) – асимптотическое выражение для искомой собственной функции y(x) при x®¥; c – константа сшивки решения в некоторой достаточно удаленной точке x=b, y(b)=cy(l, b). Если задача рассматривается на конечном отрезке [a, b], следует принять c=0. Пакет SLIPH4М позволяет решать следующие задачи для разностной аппроксимации задачи Ш–Л на равномерной сетке узлов wh отрезка a£x£b. · Частичная задача, когда по заданному начальному приближению {l0, y0(x)} вычисляется ближайшее к нему решение {l*, y*(x)} задачи (2)–(5). · Вычисление спектра (или его части) разностной задачи, аппроксимирующего соответствующую часть спектра задачи (2)–(5). Точность вычисления является величиной O(h4) и совпадает с точностью используемой разностной аппроксимации задачи (2)–(5). Методы решения задачи Итерационные схемы на основе НАМН. Задача (2)–(5) является нелинейным функциональным уравнением (1). Согласно НАМН [2], задача (1) заменяется эволюционным уравнением по непрерывному параметру t (0£t<¥)
с начальным условием
Здесь j¢ – производная Фреше j,
При достаточно общих предложениях на j(z) имеем Один шаг с номером k итерационного процесса заключается в следующем: 1. Решить краевую задачу для функции vk
где при вычисленных на предыдущем шаге (k–1) значениях lk, yk(x). 2. Вычислить поправку mk для собственного значения lk с помощью выражения
3. Найти новые приближения lk+1 и yk+1, k=0, 1, 2, …,
где tk определяется специальными алгоритмами. Итерации прекращаются, если dk где e>0 – заданное малое число, невязка dk определяется соответствующей разностной аппроксимацией для одной из формул:
Модифицированный алгоритм. Эта процедура является обобщением метода обратных итераций с фиксированным сдвигом 1. Решить две краевые задачи, отличающиеся правыми частями (i=1, 2), относительно функций
при известных с предыдущего шага (с номером k–1) значениях lk, yk(x). 2. Вычислить поправку mk к собственному значению по формуле mk=
3. Найти следующие приближения lk+1 и yk+1, k=0, 1, 2, …,
4. Для самосопряженного оператора в (2) для приближения yk+1(x) к собственной функции yn(x) выполнить ортогонализацию приближения по отношению ко всем найденным собственным функциям
5. Нормировать приближенную собственную функцию
Операции (20), (21) позволяют дополнительно подавлять вычислительные погрешности. Изменение сдвига Для нахождения решения
где Дискретное представление. Решение краевых задач (9), (10) и (16), (17) осуществляется с помощью метода конечных разностей на равномерной сетке wh. Эта задача аппроксимируется с помощью разностных формул с точностью аппроксимации O(h4). При выводе разностных формул используется прием повышения порядка точности аппроксимации на решении уравнений. Это дало возможность построить трехточечные разностные формулы с точностью аппроксимации O(h4) в узлах сетки с номерами i=3, …, N–2. В приграничных (i=2, N–1) и граничных (i=1, N) узлах используются пятиточечные схемы того же порядка точности. Формулы строятся так, чтобы коэффициенты уравнений (2)–(4) использовались только во внутренних узлах сетки wh. Это важно в тех задачах, где коэффициенты уравнения в граничных точках имеют особенности. Интегрирование в формулах (11), (15) и (18) выполняется с помощью квадратурной формулы Симпсона точности порядка O(h4). Полученные дискретные краевые задачи решаются методом прогонки. В случае p(x)º0 выведенная разностная схема совпадает со схемой Нумерова. Алгоритм вычисления начальных приближений. Данный алгоритм основан на решении двух встречных задач Коши. Для первой (x³a) ставятся начальные условия в точке x=a, где условие (3) дополняется условием на производную, если d1=0. Аналогичное условие для второй задачи (x£b) ставится в точке x=b. Тогда задача отыскания собственных значений сводится к отысканию корней функции T(l)º
появляющейся из условия равенства логариф- мических производных для решений двух задач Коши в некоторой внутренней точке отрезка xmÎ[a, b]:
Если задачи Коши решать приближенно с помощью трехточечной разностной схемы точности O(h2), где h – шаг равномерной сетки wh, а функции dj(l), fj(l) – полиномы некоторой степени от
Итерационный процесс (25) прекращается при одновременном выполнении двух условий:
где eT>0 – заданное малое число. При определении hn с заданной точностью одновременно получается и приближенное значение соответствующей сеточной собственной функции yn(x), xÎwh. Алгоритмы вычисления итерационного параметра tk. Вычисление итерационного параметра tk связано с изменением невязки dk в ходе итераций. Приведем алгоритмы выбора tk, в которых t0 – некоторое заданное значение 0 1) tkºt0. (27) Этот алгоритм при достаточно малом t0 обычно применяется при плохих начальных приближениях с целью проверить возможность сходимости от таких приближений. Сходимость при этом очень медленная. При tkº1 получается классическая схема Ньютона. 2) где dk определяется по формуле (14). Этот алгоритм аналогичен широко распространенному способу выбора шага интегрирования в стандартных программах решения задачи Коши, вычисления интегралов. Алгоритм рекомендуется применять при хороших начальных приближениях. Он обеспечивает быструю сходимость, однако не всегда устойчив. 3) где dk определяется по формуле (14). Этот алгоритм более устойчив и обеспечивает сходимость в достаточно широкой области начальных приближений, однако зависит от задания t0. 4) где dk определяется по формуле (15), dk(1) – невязка на итерации с номером k для tk=1. 5) На равномерной сетке wt на отрезке [0, 1] с шагом Dt вычисляется такое значение tk, которому соответствует минимальная невязка. Этот алгоритм более общий, чем по формуле (30), хотя и требует большего объема вычислений. Недостатком алгоритмов, использующих формулы (27)–(29), является эмпирическое задание начального значения параметра t0. Алгоритмы вычисления значения параметра t0. В программе реализованы два новых алгоритма для вычисления t0:
где невязка dk определяется по формуле (14), d1(1) – невязка на первой итерации (k=1) для t=1. Ограничение: 0,1£t0£1. Их применение позволяет сократить число итераций, что показано при решении ряда примеров, представленных в [3]. Численный пример В качестве примера использования программы SLIPH4М рассмотрим задачу о вычислении колебательных уровней энергии и волновых функций молекулы водорода [5]. Задача о молекуле водорода и ее ионах является фундаментальной в молекулярной физике. В этой области разработаны достаточно точные методы решения обратной спектральной задачи, то есть построения потенциальных энергетических функций по наборам спектроскопических данных, известных обычно с большой точностью. Имея эти потенциальные кривые, можно вычислить волновые функции молекулы и ее основные характеристики. Спектроскопические данные об уровнях энергии молекулы водорода и вычисленная в соответствии с ними потенциальная энергетическая кривая содержатся в работе [5]. Рассмотрим решение с помощью обсуждаемого численного метода и пакета SLIPH4М прямой спектральной задачи для молекулы водорода, то есть вычисление уровней энергии и волновых функций по приведенной в работе [5] таблице потенциальной кривой. Наличие большого количества расчетов и измерений уровней энергии H2 делает этот пример особенно интересным для тестирования пакета, а результаты расчетов можно сравнить со спектроскопическими данными [5]. Уровни энергии E и волновые функции y(x) молекулы водорода находятся как собственные значения и собственные решения радиального уравнения Шредингера:
на полуоси 0£x<¥ с граничными условиями y(0)=y(¥)=0, (34) где M – приведенная масса квантово-механической системы; L – орбитальный момент. В работе [5] содержится таблица III, в которой приведены экспериментальные значения уровней энергии молекулы водорода при значениях 2M=1836,109, L=0. При этом потенциал уравнения (33) имеет вид: V(x)=2M[U(x)+1], (35) где U(x) – потенциальная кривая, восстановленная по экспериментальному спектру и заданная в виде таблицы с неравномерным шагом на интервале 0,4£x£10 с 7 десятичными знаками после запятой. Для численного решения задачи (33)–(34) с помощью рассматриваемого в данной работе метода условия ограниченности (34) для волновой функции дискретного спектра аппроксимируются граничными условиями на отрезке 0£x£10: y(0)=0, (36)
Краевое условие (37) является приближением асимптотического поведения волновой функции
Рассматривается условие нормировки функции (5) при значениях a=0, b=10, c=0,
Поскольку в таблице III работы [5] значения Ev колебательных уровней энергии H2 в единицах (eV) приведены с четырьмя десятичными знаками после запятой, которые будем считать точными при тестировании, авторами первоначально выбрана равномерная сетка узлов wh с шагом h=0,005 на отрезке 0£x£10. Для приближенного задания функции U(x) в узлах этой сетки на отрезке 0,4£x£10 использовались как квадратичная интерполяция, так и сплайн-аппроксимация второго порядка исходных табличных данных. Оба способа дали одинаковые результаты в пределах точности разностной аппроксимации. При x<0,4 функция U(x) экстраполировалась с помощью выражения
соответствующего кулоновскому взаимодействию вблизи нуля. Константа r выбиралась из условия U(0,4)=u(0,4). При использовании пакета SLIPH4М в задаче (2)–(4) выполнена замена l=E, p(x)=0, q(x)= –V(x), r(x)= –2M, a=0, b=10. Для перевода вычисленных значений Ev из единиц задачи (units of test (UT)) в электрон-вольты использовалась формула Ev(eV)=–Ev(UT)*27,2107. Кроме того, проведен пересчет вычисленных значений Ev(eV) к началу отсчета E0(eV), поскольку это же начало принято для табличных значений работы [5]. Расчеты выполнены для двух значений приведенной массы 2M: из работы [5] и уточненной в соответствии с новыми данными. Результаты расчетов и их сравнение с данными работы [5] представлены в таблице. Сравнение показывает, что абсолютные значения разностей между ними таковы:
где значения Разумеется, что на точность решения этой задачи оказывают влияние ошибки, связанные с интерполяцией, а в еще большей мере – с экстраполяцией табличной функции U(x) с помощью формулы (40), поскольку ее точное асимптотическое поведение вблизи нуля неизвестно.
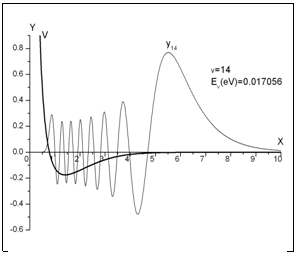
Помимо вычисленных значений Ev, соответствующих экспериментальным данным, в таблице приведено собственное значение E14 задачи (33), (36), (37), вычисленное с помощью рассматриваемого алгоритма (волновая функция y14(x) и потенциал V(x) изображены на рисунке), для которого нет соответствующего экспериментального уровня энергии. Следовательно, вычисленная часть спектра задачи (33), (36), (37) перекрывает экспериментальный спектр, то есть пакет SLIPH4М может успешно применяться в задачах, аналогичных рассмотренной. Для v=14 точность решения O(hp) (p=4) подтверждена вычислениями на последовательности трех сгущающихся сеток с шагами h=0,005 (N=2001), h/2, h/4 и получением значения отношения Рунге для zh=(lh, yh):
то есть порядок p=log2s>4.
Авторы благодарят профессора И.В. Пузынина (ОИЯИ, г. Дубна) за постоянный интерес, помощь и поддержку. Литература 1. Самарский А.А. Теория разностных схем. М.: Наука, 1983. С. 258–276. 2. Пузынин И.В. [и др.]. Обобщенный непрерывный аналог метода Ньютона для численного исследования некоторых квантово-полевых моделей; Физика элементарных частиц и атомного ядра (ЭЧАЯ). 1999. Т. 30. Вып. 1. С. 210–265. 3. Пузынин И.В., Пузынина Т.П., Во Чонг Тхак. SLIPM – программа на языке MAPLE для численного решения частичной проблемы Штурма–Лиувилля на основе непрерывного аналога метода Ньютона // Вестн. РУДН: сер. Математика. Информатика. Физика. 2010. № 2. Вып. 2. С. 90–98. 4. Пузынин И.В., Пузынина Т.П., Стриж Т.А. SLIPH4 – программа для численного решения задачи Штурма–Лиувилля // Сообщения ОИЯИ, P11-87-332, Дубна, 1987. 5. Sharp T.E. Potential-energy curves for molecular hydrogen and its ions // Atomic Data and Nuclear Data Tables, 1971. Vol. 2, pp. 119–169. | ||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2817&page=article |
Версия для печати Выпуск в формате PDF (5.05Мб) Скачать обложку в формате PDF (1.39Мб) |
| Статья опубликована в выпуске журнала № 3 за 2011 год. |
Назад, к списку статей



 (3)
(3) (4)
(4) (5)
(5) .
. (6)
(6) . (7)
. (7) (8)
(8) , где
, где  – решение задачи (2)–(5), ближайшее к z0. Для приближенного решения задачи (6), (7) методом Эйлера введем дискретное множество узлов {tk}={tk=tk+1–tk}, k=0, 1, 2, ….
– решение задачи (2)–(5), ближайшее к z0. Для приближенного решения задачи (6), (7) методом Эйлера введем дискретное множество узлов {tk}={tk=tk+1–tk}, k=0, 1, 2, ….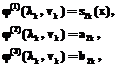 (9)
(9) (10)
(10) .(11)
.(11) ,
, , (12)
, (12) j=1, 2, 3, (14)
j=1, 2, 3, (14) , xÎwh. (15)
, xÎwh. (15) . При довольно грубых приближениях к собственной функции она обеспечивает сходимость к решению
. При довольно грубых приближениях к собственной функции она обеспечивает сходимость к решению 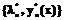 , где
, где  – ближайшее к
– ближайшее к  и
и  :
: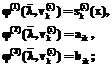 (16)
(16)
 (17)
(17)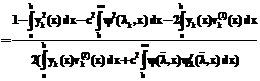 .(18)
.(18) . (19)
. (19) , m=0, 1, 2, …, n–1, по формуле
, m=0, 1, 2, …, n–1, по формуле . (20)
. (20) . (21)
. (21) в качестве
в качестве  , m=0, 1, 2, …, (22)
, m=0, 1, 2, …, (22) – вычисленное собственное значение; x>0 – параметр сдвига.
– вычисленное собственное значение; x>0 – параметр сдвига. , (23)
, (23) . (24)
. (24) , что справедливо для широкого круга практических задач, то функция T(h) является полиномом. Его корни hn находятся по методу Ньютона с исключением уже найденных корней (k – номер итерации):
, что справедливо для широкого круга практических задач, то функция T(h) является полиномом. Его корни hn находятся по методу Ньютона с исключением уже найденных корней (k – номер итерации): . (25)
. (25) и
и  , (26)
, (26) (28)
(28) (29)
(29) , (30)
, (30) , (31)
, (31)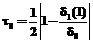 , (32)
, (32)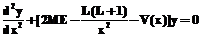 (33)
(33)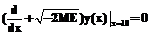 . (37)
. (37) при x®¥. (38)
при x®¥. (38) . (39)
. (39)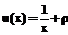 , (40)
, (40) ,
, считаются точными.
считаются точными.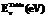 из работы [5]
из работы [5] (41)
(41) Расчеты выполнялись на PC (Intel(R) Pentium(R) M processor 1.8GHz) в системе Maple версии 13. Переменное окружение Digits управляет числом цифр, которые Maple использует при вычислениях с числами с плавающей запятой. При Digits=10 алгоритм в пакете SLIPH4M по умолчанию не сходится, поэтому в пакете SLIPH4M Digits=20. Начальное приближение дает невязку по формуле (14) dk»10+2–10–2. Итерации осуществлялись с выбором параметра tk согласно формуле (29) (t0=0,1), причем в процессе уточнения невязка достигала величины »10–8–10–11 в среднем за 11 итераций.
Расчеты выполнялись на PC (Intel(R) Pentium(R) M processor 1.8GHz) в системе Maple версии 13. Переменное окружение Digits управляет числом цифр, которые Maple использует при вычислениях с числами с плавающей запятой. При Digits=10 алгоритм в пакете SLIPH4M по умолчанию не сходится, поэтому в пакете SLIPH4M Digits=20. Начальное приближение дает невязку по формуле (14) dk»10+2–10–2. Итерации осуществлялись с выбором параметра tk согласно формуле (29) (t0=0,1), причем в процессе уточнения невязка достигала величины »10–8–10–11 в среднем за 11 итераций.