В последнее десятилетие интенсивно развиваются методы компьютерного анализа и обобщения объектов, заданных не только количественными дискретными признаками, но и набором качественных вербальных характеристик. Особое внимание уделяется анализу и обобщению свойств различных изображений, в частности, функциональных зависимостей, представленных плоскими графиками.
В природе существуют процессы, для которых характерно сохранение отдельных свойств графика на фоне изменяющихся в некотором диапазоне координат его отдельных точек. Плоские кривые являются основными видами зависимостей, анализируемыми врачом при выявлении симптомов и постановке диагноза. Если для построения кривых используются точные количественные значения, процедуру анализа во многих случаях можно полностью автоматизировать. Однако возможны ситуации, когда число классов, объединяющих близкие по форме кривые, велико и до конца не выявлено или когда для построения кривых используются неточные, приблизительные по своей природе значения. В этих случаях возникает проблема классификации нечетких графиков, которую целесообразно решать, опираясь на правила определения качественных топологических характеристик на основе мягких вычислений.
Задача оценки топологических характеристик нечетких ломаных линий
 Рассмотрим процесс, описываемый зависимостью вида y=f(x), которую графически можно представить ломаной линией. Процесс находится под наблюдением, и зависимость регистрируется многократно: {y=f(x)j}. Известно, что абсциссы узловых точек всех графиков заданы с помощью одного и того же вектора X=(x1, x2, …, xN+1), составляющие которого не изменяются во времени. Ординаты узловых точек с течением времени могут изменяться, образуя N+1 подмножества составляющих вектора Y=({y1i}, {y2r}, …, {y(N+1)t}). Если ломаную линию представить как последовательность узловых точек с координатами (xi, yi),
Рассмотрим процесс, описываемый зависимостью вида y=f(x), которую графически можно представить ломаной линией. Процесс находится под наблюдением, и зависимость регистрируется многократно: {y=f(x)j}. Известно, что абсциссы узловых точек всех графиков заданы с помощью одного и того же вектора X=(x1, x2, …, xN+1), составляющие которого не изменяются во времени. Ординаты узловых точек с течением времени могут изменяться, образуя N+1 подмножества составляющих вектора Y=({y1i}, {y2r}, …, {y(N+1)t}). Если ломаную линию представить как последовательность узловых точек с координатами (xi, yi),  , тогда с учетом вида элементов вектора Y формируется множество ломаных линий {Linj},
, тогда с учетом вида элементов вектора Y формируется множество ломаных линий {Linj},  :
:
Linj=(x1, y1jÎ{y1i}), (x2, y2jÎ{y2r}), …,
(xN+1, yN+1,jÎ{y(N+1)t}). (1)
Предположим, что все ломаные имеют хотя бы одно общее топологическое свойство, например, соответствуют убывающим зависимостям (рис. 1). Но тогда {Linj} можно рассматривать как график, построенный на множестве точек с нечетко определенными ординатами (см. табл.). Для оценки ординат используется набор термов TY, включающий следующие упорядоченные по возрастанию значения: TY1 – малые, TY2 – средние и т.д. с соответствующими функциями принадлежности.
|
График y=f(x)j
|
Y
|
y1
|
y2
|
…
|
yN+1
|
|
X
|
x1
|
x1
|
…
|
xN+1
|
|
График TY=f(x)j
|
TY
|
TYr
|
TYj
|
…
|
TY
|
|
m
|

|
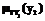
|
…
|

|
Любую ломаную линию можно представить как совокупность упорядоченных отрезков, каждый из которых соединяет два соседних узла:
Oi=(xi, yi), (xi+1, yi+1),  .
.
Основными характеристиками отрезка являются длина и направление. В декартовой системе координат длина определяется как
 , (2)
, (2)
где  – проекция i-го отрезка на ось ОХ;
– проекция i-го отрезка на ось ОХ;  – проекции i-го отрезка на ось OY.
– проекции i-го отрезка на ось OY.
Учитывая, что в DOi надо объединять четкие и нечеткие значения, оценку длины отрезка можно найти по формулам нечеткой арифметики [1].
Для нечеткой оценки направления отрезка (NP) эксперты используют термы TO1 – убывающий, TO2 – ровный, TO3 – возрастающий, усиливая или ослабляя эти свойства модальностями (сильно, слабо и т.п.). В классической постановке задачи для фазификации необходимо также построение функций принадлежности для каждого из перечисленных термов. При таком подходе общее число функций принадлежности возрастает: m=mTOÈmTY. Однако, если множество mTY ввести достаточно просто, так как это связано с чисто метрическими оценками длины, формирование функций принадлежности более сложных отношений (mTO) может привести к дополнительным ошибкам и будет зависеть от масштаба изображения по оси ОХ. Необходимо сформулировать правила, позволяющие выполнить переход к вербальным оценкам направления отрезка (NP) на основе только нечетких оценок ординат его концов.
Предположим, что ординаты начала и конца отрезка принадлежат разным нечетким множествам. Пусть k, m – индексы термов, которые соответственно определяют нечеткое множество, включающее ординату начальной точки (yj), и нечеткое множество, включающее ординату конечной точки (yj+1) (рис. 2). Тогда,
если yjÎTYk и yj+1ÎTYm, то NP=TO3/ ; (3)
; (3)
если yjÎTYm и yj+1ÎTYk, то NP=TO1/ .
.
Оценка функции принадлежности отрезка соответствующему нечеткому множеству такова:
 (4)
(4)
Предположим, что k=m, тогда ординаты концов отрезка принадлежат одному нечеткому множеству (yj, yj+1ÎTYk). Известно, что для функции принадлежности симметричной формы можно выделить два подмножества  , используя участки слева и справа от mk=1 (рис. 3).
, используя участки слева и справа от mk=1 (рис. 3).
Тогда, если  , оценка yj по лингвистической шкале будет некоторым преувеличением, а соответствующая yj+1 даст преуменьшение оценки ординаты. Такие результаты получаются вследствие применения правила фази-объединения [2] нечетких множеств:
, оценка yj по лингвистической шкале будет некоторым преувеличением, а соответствующая yj+1 даст преуменьшение оценки ординаты. Такие результаты получаются вследствие применения правила фази-объединения [2] нечетких множеств:
 .
.
Примем допущение о возможном уменьшении интерпретации оценки j-й и увеличении интерпретации оценки (j+1)-й, тогда
 и
и
 при
при  . (5)
. (5)
Если ординаты концов отрезка принадлежат левому подмножеству  , то есть существует преувеличение в оценках yj и yj+1, то в соответствии с (5) обе ординаты перейдут в правое подмножество предшествующего терма
, то есть существует преувеличение в оценках yj и yj+1, то в соответствии с (5) обе ординаты перейдут в правое подмножество предшествующего терма  . Тогда,
. Тогда,
если  , то
, то  ,
,
если  , то
, то 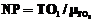 ,
,
если  и
и  ,
,
то  ,
,
если  , то
, то  .
.
если yj=yj+1,
 то отрезок ровный:
то отрезок ровный:  . (6)
. (6)
Оценка функции принадлежности отрезка множеству TOi (i=1, 2) определяется как  .
.
Предположим, что i-й отрезок является убывающим. Если начало отрезка использовать как центр окружности, а его конец перемещать против часовой стрелки, отрезок последовательно будет переходить из нечеткого множества TO1 (убывающие) в TO2 (ровные), а затем в TO3 (возрастающие). Если рассматривать только нормализованные функции принадлежности, имеющие одну общую точку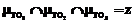 (например Z=0,5), то каждый отрезок будет принадлежать двум нечетким множествам [3].
(например Z=0,5), то каждый отрезок будет принадлежать двум нечетким множествам [3].
Если 
то  . (7)
. (7)
Если 
то  .
.
Набор правил (3–7) можно применять также для аппроксимации отдельных участков кривых отрезками, связывающими произвольные точки.
Результаты распознавания принадлежности отрезков, составляющих ломаную линию, одному из нечетких множеств можно представить в виде квадратной матрицы M_ot=[mi,j]. Каждый ее элемент представляет наименование множества, которому принадлежит отрезок, начинающийся в i-й и заканчивающийся в j-й точке. Элементы на главной диагонали не имеют смысла и не рассматриваются. Интерпретация отрезков, связывающих узлы ломаной линии, складывается из элементов, образующих диагональ правее главной. Так как матрица содержит описания всех отрезков, которые можно построить на заданном множестве узловых точек, то ее можно рассматривать как описание и ломаной линии, и различных вариантов ее аппроксимации [4]. На основе анализа матрицы отрезков определяется направление всей ломаной линии. Учитывая, что матрица симметрична главной диагонали, анализируется только ее верхняя половина. Применяется стратегия голосования – элементы голосуют своими функциями принадлежности, после чего выбирается терм, имеющий наибольшее численное значение.
Основными топологическими свойствами ломаных линий являются их форма и характер взаиморасположения на плоскости. По форме принято выделять выгнутые, вогнутые и пилообразные зависимости. В работе [4] рассмотрен алгоритм определения формы линии на основе нечетких оценок отрезков.
Характер взаиморасположения двух ломаных линий определяется расстоянием между ними (рядом, далеко, близко), пересечением (есть или нет), касанием (есть общие точки или нет). Для оценки расстояния между двумя линиями будем сравнивать узловые точки с одинаковыми абсциссами, принадлежащими разным линиям. Например, найдем расстояние между точкой (xi, y1ÎTY1), принадлежащей первой ломаной, и точкой (xi, y2ÎTY3) на второй ломаной (рис. 4).
Для оценки нечеткой разности Del/mdel= =TY3/m3(y1)–TY1/m1(y2) предлагается перейти от терм-множества TY к новой индексной шкале путем преобразования нечеткой переменной в число с плавающей запятой:
 (8)
(8)
где W – оценка по новой шкале нечеткой переменной TYi/mi,  – индекс терма.
– индекс терма.
Для функций принадлежности без участков dm/dy=0 алгоритм перевода ординат узловых точек в индексную шкалу включает следующие шаги.
1. Повторная фазификация ординаты y1 по правилу пересечения нечетких множеств. В результате получаем TYi/(min(mi, mi-1)).
2. Индекс терма ( ), к нечеткому множеству которого отнесен y1, далее рассматривается как целая часть числа W, а значение функции принадлежности minmi(y1) как его дробная часть.
), к нечеткому множеству которого отнесен y1, далее рассматривается как целая часть числа W, а значение функции принадлежности minmi(y1) как его дробная часть.
В итоге получаются оценки ординат узловых точек в виде чисел с плавающей запятой, и расстояние между точками определяется как разность полученных чисел. Для обратного перевода оценки расстояния WDel из условной индексной шкалы в лингвистическую необходимо:
- в соответствии с полученным значением целой части WDel определить индекс терма  , к нечеткому множеству которого относится оценка расстояния Del;
, к нечеткому множеству которого относится оценка расстояния Del;
- используя значение дробной части WDel, по правилу дополнения определить 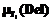 .
.
Лингвистический интерпретатор аудиограмм
 Рассмотренные алгоритмы послужили основой для создания математического и программного обеспечения комплекса, решающего задачи лингвистической интерпретации результатов тональных исследований слуховой функции. В современных аудиометрах кривые порогов слышимости представляют в виде специального графика – аудиограммы. Точки, характеризующие потерю слуха, соединяются в две ломаные линии – кривые порогов слышимости по воздушному и костному проведению. По виду аудиограммы пациента врач делает заключение о локализации очага заболевания по отделам органов слуха.
Рассмотренные алгоритмы послужили основой для создания математического и программного обеспечения комплекса, решающего задачи лингвистической интерпретации результатов тональных исследований слуховой функции. В современных аудиометрах кривые порогов слышимости представляют в виде специального графика – аудиограммы. Точки, характеризующие потерю слуха, соединяются в две ломаные линии – кривые порогов слышимости по воздушному и костному проведению. По виду аудиограммы пациента врач делает заключение о локализации очага заболевания по отделам органов слуха.
Рассматриваемый программный комплекс полностью автоматически осуществляет процедуры анализа и интерпретации кривых порогов слышимости. Во время анализа этих графиков для каждой кривой определяются направление, фор- ма и ее положение относительно оси абсцисс. Для всей аудиограммы оцениваются величи- на расстояния между кривыми (костно-воздуш- ный интервал), наличие пересечений, обрывов кривых.
В состав программного комплекса входят редактор функций принадлежности, редактор БД (архив аудиограмм), модули фазификации исходных точек графиков, формирования матрицы отрезков, формирования нечетких оценок топологических характеристик пороговых кривых и лингвистической интерпретации аудиограммы.
 Программа написана на языке С# для выполнения в среде .NET Framework 2.0 и выше. Комплекс может работать с наборами аудиограмм в табличном виде, которые загружаются из текстовых файлов или из БД СУБД Access. Аудиограммы можно просмотреть как в табличном виде, так и в виде графиков.
Программа написана на языке С# для выполнения в среде .NET Framework 2.0 и выше. Комплекс может работать с наборами аудиограмм в табличном виде, которые загружаются из текстовых файлов или из БД СУБД Access. Аудиограммы можно просмотреть как в табличном виде, так и в виде графиков.
Значения функций принадлежности для термов лингвистической переменной «Потери слуха на частоте (,,)» хранятся в отдельном файле, который редактируется специальным графическим редактором.
Каждую аудиограмму можно представить в виде ее нечеткой модели и матрицы отрезков. Матрица отрезков представляется как в символьном виде, так и в виде специальной цветовой схемы KG.
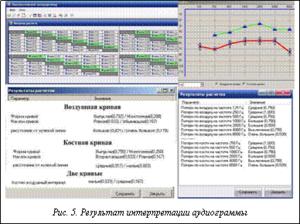
Цветовая схема матрицы отрезков является дополнительным инструментом, позволяющим эксперту контролировать построение лингвистических оценок топологических свойств ломаных линий. Пример полной интерпретации аудиограммы приведен на рисунке 5.
Предложенные алгоритмы позволяют создавать процедуры анализа топологических свойств графиков, инвариантные к масштабу изображения. В рассмотренной задаче все выделенные топологические характеристики плоских кривых найдены с использованием только функций принадлежности, характеризующих величину ординат точек. Это означает, что помощь эксперта необходима лишь при оценке очень простых качественных характеристик (большие, малые и т.п.), которые человек обычно легко идентифицирует. На основе рассмотренного комплекса создана программа автоматического анализа результатов тональной аудиометрии при исследовании порогов слышимости человека.
Литература
1. Штовба С.Д. Введение в теорию нечетких множеств и нечеткую логику. URL: http://matlab.exponenta.ru/fuzzylogic/ bookl/index.php (дата обращения: 18.01.2011).
2. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений; [пер. с англ.]. М.: Мир, 1976.
3. Нечеткие модели для экспертных систем в САПР / Н.Г. Малышев, Л.С. Берштейн, А.В. Боженюк. М.: Энергоатомиздат, 1991. 136 с.
4. Миловидов А.А., Филатова Н.Н. Построение качественных характеристик аудиометрических кривых на основе нечетких оценок порогов слышимости // Нечеткие системы и мягкие вычисления–2009: сб. науч. тр. Т. 1. Волгоград, 2009. С. 194–203.



 Рассмотрим процесс, описываемый зависимостью вида y=f(x), которую графически можно представить ломаной линией. Процесс находится под наблюдением, и зависимость регистрируется многократно: {y=f(x)j}. Известно, что абсциссы узловых точек всех графиков заданы с помощью одного и того же вектора X=(x1, x2, …, xN+1), составляющие которого не изменяются во времени. Ординаты узловых точек с течением времени могут изменяться, образуя N+1 подмножества составляющих вектора Y=({y1i}, {y2r}, …, {y(N+1)t}). Если ломаную линию представить как последовательность узловых точек с координатами (xi, yi),
Рассмотрим процесс, описываемый зависимостью вида y=f(x), которую графически можно представить ломаной линией. Процесс находится под наблюдением, и зависимость регистрируется многократно: {y=f(x)j}. Известно, что абсциссы узловых точек всех графиков заданы с помощью одного и того же вектора X=(x1, x2, …, xN+1), составляющие которого не изменяются во времени. Ординаты узловых точек с течением времени могут изменяться, образуя N+1 подмножества составляющих вектора Y=({y1i}, {y2r}, …, {y(N+1)t}). Если ломаную линию представить как последовательность узловых точек с координатами (xi, yi),  , тогда с учетом вида элементов вектора Y формируется множество ломаных линий {Linj},
, тогда с учетом вида элементов вектора Y формируется множество ломаных линий {Linj},  :
:
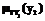

 .
. , (2)
, (2) – проекция i-го отрезка на ось ОХ;
– проекция i-го отрезка на ось ОХ;  – проекции i-го отрезка на ось OY.
– проекции i-го отрезка на ось OY. ; (3)
; (3) .
. (4)
(4) , используя участки слева и справа от mk=1 (рис. 3).
, используя участки слева и справа от mk=1 (рис. 3). , оценка yj по лингвистической шкале будет некоторым преувеличением, а соответствующая yj+1 даст преуменьшение оценки ординаты. Такие результаты получаются вследствие применения правила фази-объединения [2] нечетких множеств:
, оценка yj по лингвистической шкале будет некоторым преувеличением, а соответствующая yj+1 даст преуменьшение оценки ординаты. Такие результаты получаются вследствие применения правила фази-объединения [2] нечетких множеств: .
. и
и при
при  . (5)
. (5) , то есть существует преувеличение в оценках yj и yj+1, то в соответствии с (5) обе ординаты перейдут в правое подмножество предшествующего терма
, то есть существует преувеличение в оценках yj и yj+1, то в соответствии с (5) обе ординаты перейдут в правое подмножество предшествующего терма  . Тогда,
. Тогда, , то
, то  ,
, , то
, то 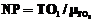 ,
, и
и  ,
, ,
, , то
, то 
 . (6)
. (6) .
.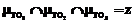 (например Z=0,5), то каждый отрезок будет принадлежать двум нечетким множествам [3].
(например Z=0,5), то каждый отрезок будет принадлежать двум нечетким множествам [3].
 . (7)
. (7)
 .
. (8)
(8) – индекс терма.
– индекс терма. ), к нечеткому множеству которого отнесен y1, далее рассматривается как целая часть числа W, а значение функции принадлежности minmi(y1) как его дробная часть.
), к нечеткому множеству которого отнесен y1, далее рассматривается как целая часть числа W, а значение функции принадлежности minmi(y1) как его дробная часть. , к нечеткому множеству которого относится оценка расстояния Del;
, к нечеткому множеству которого относится оценка расстояния Del; .
.

