Выделение границ – один из основных шагов задач обработки изображений, распознавания и анализа образов, компьютерного зрения. Под детекторами границ понимаются различные алгоритмы, выделяющие точки цифрового изображения, в которых резко изменяется яркость или есть другие виды неоднородностей. При этом способ определения граничной точки двухмерного изображения носит нечеткий характер, поскольку на практике редко жестко фиксируется порог, при котором яркость между двумя соседними пикселями изменяется настолько, что можно утверждать о нахождении там границы. Это одна из причин считать выделение границ нетривиальной задачей. К настоящему времени разработаны десятки различных детекторов границ (при этом некоторые из них имеют всевозможные доступные в Интернете программные реализации), что делает задачу разработки универсальных критериев оценки их достоинств и недостатков все более актуальной.
Как правило, желаемым результатом выделения границ является набор связных кривых, обозначающих границы объектов. Но, к сожалению, не всегда можно выделить границы в картинах реального мира. Границы, выделенные из подобных изображений, часто имеют такие недостатки, как фрагментированность (кривые границ не соединены между собой), отсутствие границ или наличие ложных, не соответствующих исследуемому объекту границ.
Появившиеся первыми методы выделения границ можно разделить на две основные категории: основанные на поиске максимумов (градиентные методы) и основанные на поиске нулей (методы второго порядка). Методы, основанные на поиске максимумов, восходящие к работам Sobel, Prewitt и Roberts, выделяют границы с помощью силы края, такого как величина градиента. Затем происходит поиск локальных максимумов силы края с использованием предполагаемого направления границы (как правило, это перпендикуляр к вектору градиента). Методы второго порядка, восходящие к работам Marr и Hildreth, ищут пересечения оси абсцисс выражения второй производной (обычно нули лапласиана или нули нелинейного дифференциального выражения второго порядка). В настоящее время используются и статистические методы, методы с использованием нечеткой логики, логических операторов (алгоритм Iverson), методы, основанные на согласованности фаз, и др.
Принято считать, что основные требования к детектору границ впервые были сформулированы J. Canny в 1986 году. Автору удалось сначала сформулировать содержательные требования к детектору, выразить их в виде некоторой оптимизационной задачи, а затем решить эту задачу. Детектор границ должен удовлетворять следующим трем критериям эффективности.
1. Хорошее отношение сигнала к шуму, то есть детектор должен выделять все истинные границы и при этом не выделять ложные.
2. Хорошая локализация. Точки, отмеченные как границы, должны располагаться как можно ближе к истинному положению границ.
3. Единственность отклика на границу (это требование содержится в первом критерии, однако математическая формулировка первого критерия не обеспечивает выполнение данного пункта).
Хотя детектор границ Canny был разработан на заре компьютерного зрения, он до сих пор является одним из наиболее часто используемых. Кроме частных случаев, трудно найти детектор, который работал бы существенно лучше Canny, и практически все работы по сравнительному исследованию детекторов границ содержат его в качестве своего рода эталона.
Цель настоящей работы – дать объективное представление о некоторых методах (в том числе применяемых авторами) сравнительного исследования производительности детекторов границ и об используемых при этом количественных критериях оценки качества рассматриваемых алгоритмов. Предполагается, что это поможет практическим пользователям сделать выбор того или иного детектора границ для решения своих задач более осмысленным и стимулировать дальнейший интерес к задаче количественной оценки производительности детекторов границ.
Методы оценки детекторов границ
Как и в случае с другими классами алгоритмов обработки изображений, методы оценки производительности детекторов границ можно разделить на теоретические и эмпирические. Это зависит от того, используют они теоретический анализ или рассматривают экспериментальные результаты работы того или иного алгоритма. В свою очередь, эмпирические методы подразделяются на методы, использующие ground truth (GT) оценку и так называемые методы эмпирической оценки доброкачественности (empirical goodness methods), которые эту оценку не применяют. Здесь под GT-образами понимаются изображения (как правило, созданные вручную), содержащие идеальные в понимании экспериментатора границы.
Что касается теоретических методов оценки производительности детекторов границ, в известных работах входные данные рассматриваемого алгоритма описываются математически, а его производительность определяется аналитически или путем симуляции. Для оценки были разработаны соответствующие меры. Недостатками этих работ являлись упрощенные математические модели, характеризующие входные сигнал и шум, а также сложность применения предложенных методов к современным детекторам границ из-за сложности алгоритмов последних.
Методы эмпирической оценки доброкачественности, как правило, оценивают либо форму выделяемых границ, либо вероятность правильного определения граничного пикселя на основе изучения яркости пикселей в его окрестности. Существенным недостатком данных методов в их практическом применении является то, что они не могут измерить смещение выделенных граничных пикселей относительно их истинного положения. В частности, эти методы могут давать неадекватные результаты на детекторах, использующих размытие изображения на этапе предобработки. К данной группе методов можно отнести и такие, в которых качество работы различных алгоритмов оценивают люди, выразившие желание участвовать в эксперименте. Эти исследования подтвердили некоторые сложившиеся представления об известных детекторах границ (в частности, вывод о существенности предварительной настройки их входных параметров). Однако они не решают проблему выбора оптимального детектора границ для той или иной конкретной задачи обработки изображений.
Наиболее обширное семейство методов оценки детекторов границ использует сравнение результатов работы исследуемых алгоритмов на тестовых изображениях с GT-образами. Для количественной оценки результатов основную роль здесь играют меры различий (discrepancy measures). Используются и производные от этих метрик методы оценок, например, анализ ROC-кривых [1].
К недостаткам ранних работ по данной тематике можно отнести то, что используемые в них GT-образы создавались искусственно или брались несложные реальные изображения с легко идентифицируемыми границами. На практике нередко встречаются достаточно трудные для распознавания ситуации, и это сужает область применения указанных методов. Некоторые авторы отмечали, что небольшие изменения в используемых искусственных тестовых (и соответствующих GT) изображениях приводили к различным оценкам тестируемых детекторов границ (в разных ситуациях разные детекторы оказываются лучшими). Так возник вопрос о полноте набора тестовых изображений, используемых в методологии с использованием GT-образов. Указанные недостатки были изучены и частично преодолены в последующих работах по данной тематике (в частности, это вызвало совершенствование применяемых тестовых и GT-изображений). Стали чаще использоваться изображения, моделирующие сложные для выделения границ ситуации (например, на рис. 1 представлено несколько изображений из базы тестовых образов системы PICASSO [2]).
 На рисунке 1 каждому изображению соответствует определенная сложная ситуация, связанная с наличием границы изменяющегося контраста. В работе [2] тестировались шесть известных алгоритмов выделения границ: Canny, Rothwell, Heitger, Black, Smith and Iverson. В частности, было установлено нестабильное поведение всех алгоритмов на изображениях, содержащих подобные границы, при малых поворотах, сдвигах и растяжениях этих изображений. Использовались и упрощенные версии изображений (рис. 1), содержащие только границы постоянного контраста, при этом поведение алгоритмов на них было относительно стабильным. Тем самым сочетание простых и усложненных изображений сделало тестирование более результативным.
На рисунке 1 каждому изображению соответствует определенная сложная ситуация, связанная с наличием границы изменяющегося контраста. В работе [2] тестировались шесть известных алгоритмов выделения границ: Canny, Rothwell, Heitger, Black, Smith and Iverson. В частности, было установлено нестабильное поведение всех алгоритмов на изображениях, содержащих подобные границы, при малых поворотах, сдвигах и растяжениях этих изображений. Использовались и упрощенные версии изображений (рис. 1), содержащие только границы постоянного контраста, при этом поведение алгоритмов на них было относительно стабильным. Тем самым сочетание простых и усложненных изображений сделало тестирование более результативным.
Используемые меры различий
Как уже отмечалось, основными характеристиками хорошего детектора границ являются высокий процент правильно выделенных граничных пикселей (высокий уровень детектирования) и высокая степень локализации (близость выделенных пикселей к соответствующим им на GT-изображении). К настоящему времени не удалось создать меру, одинаково эффективно оценивающую эти две характеристики. Отчасти это связано с тем, что, как было отмечено J. Canny, имеет место своего рода принцип неопределенности между высоким уровнем детектирования и высокой степенью локализации. Соответственно, для оценки данных характеристик детекторов границ используются разные меры различий. В частности, в работе [3], посвященной исследованию мер различий для детекторов границ, они подразделялись на меры оценки качества детектирования и меры оценки локализации.
Приведем пример нескольких часто встречающихся мер оценки качества детектирования. Пусть имеются: X – растр изображения, состоящий из N пикселей; B – результат работы оцениваемого детектора границ (образ, состоящий из граничных точек); A – соответствующий GT-образ. Тогда ошибка 1-го рода определяется как 
 где n(·) – число пикселей в соответствующем множестве, то есть как отношение неправильно выделенных граничных пикселей к общему числу пикселей, не являющихся граничными.
где n(·) – число пикселей в соответствующем множестве, то есть как отношение неправильно выделенных граничных пикселей к общему числу пикселей, не являющихся граничными.
Ошибка второго рода определяется как  то есть как отношение невыделенных граничных пикселей к общему числу граничных пикселей.
то есть как отношение невыделенных граничных пикселей к общему числу граничных пикселей.
Общая ошибка классификации определяется как  где D – симметрическая разность множеств.
где D – симметрическая разность множеств.
На практике часто встречаются такие меры, как чувствительность (Sensitivity): 
 , то есть отношение правильно выделенных граничных пикселей к общему числу граничных пикселей, а также специфичность (Specificity):
, то есть отношение правильно выделенных граничных пикселей к общему числу граничных пикселей, а также специфичность (Specificity):  .
.
Чувствительность, специфичность, ошибки первого и второго рода являются исходными величинами при построении ROC-кривых, анализ которых нашел применение и в задаче оценки детекторов границ [1]. Указанные меры оценки качества детектирования неслучайно называются статистическими. Изначально они использовались в медицинской статистике при анализе диагностики различных заболеваний. Кроме того, указанные меры являются частным случаем (при двухмерной классификации) мер оценки качества классификации, широко используемых в обработке данных дистанционного зондирования.
К мерам оценки качества детектирования можно отнести и евклидову среднеквадратическую метрику, которая применяется при сравнении двух полутоновых изображений: 
 , где f(x) – величина яркости изображения f в точке x. В случае детекторов границ f и g могут принимать значения 0 или 1 в зависимости от того, является ли точка соответствующего изображения граничной или нет. Сюда же относятся эквивалентные (в данной ситуации) отношения сигнала к шуму, пиковое и среднеквадратическое. Эти отношения используются и на этапе предобработки изображений (перед выделением границ) для оценки соответствующих фильтров.
, где f(x) – величина яркости изображения f в точке x. В случае детекторов границ f и g могут принимать значения 0 или 1 в зависимости от того, является ли точка соответствующего изображения граничной или нет. Сюда же относятся эквивалентные (в данной ситуации) отношения сигнала к шуму, пиковое и среднеквадратическое. Эти отношения используются и на этапе предобработки изображений (перед выделением границ) для оценки соответствующих фильтров.
Указанные меры оценки качества детектирования имеют большое практическое применение, при этом неоднократно отмечались их недостатки [3]. Наиболее слабым местом является то, что различия между изображениями A и B определяются по общему числу расхождений между ними безотносительно к образу, который эти изображения представляет. Так, небольшой сдвиг в оцениваемой карте границ относительно GT-изображения, затрагивающий большое число пикселей, но не меняющий форму образа (к примеру, на оцениваемом изображении та же чашка, что и на GT, но слегка сдвинутая по отношению к последнему), приведет к плохим значениям оценки качества детектирования. В то же время небольшие искажения, затрагивающие незначительное число пикселей, но существенно меняющие форму изображаемого объекта (небольшие удаления линий, заполнения маленьких дырок и т.п.), дадут хорошие значения данных мер. При практическом оценивании детекторов границ с помощью этих мер следует принимать во внимание указанные недостатки. В частности, это относится к выделению границ, использующих размытие зашумленных изображений на этапе предобработки.
К мерам оценки локализации можно от- нести среднюю ошибку расстояния: 
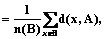 где d(X,A)=inf r(x, a), aÎA, а
где d(X,A)=inf r(x, a), aÎA, а  в рассматриваемой дискретной ситуации представляет собой метрику кратчайшего пути [3]. Сюда же относятся среднеквадратическая ошибка расстояния:
в рассматриваемой дискретной ситуации представляет собой метрику кратчайшего пути [3]. Сюда же относятся среднеквадратическая ошибка расстояния:  а также часто встречающаяся в литературе метрика Пратта
а также часто встречающаяся в литературе метрика Пратта  где k – коэффициент масштабирования, обычно полагаемый равным 1/9, а метрика кратчайшего пути нормируется таким образом, что наименьшее ненулевое расстояние между соседними пикселями равно единице. Заметим, что FOM(A, B)¹ ¹FOM(B, A), очевидно, 0
где k – коэффициент масштабирования, обычно полагаемый равным 1/9, а метрика кратчайшего пути нормируется таким образом, что наименьшее ненулевое расстояние между соседними пикселями равно единице. Заметим, что FOM(A, B)¹ ¹FOM(B, A), очевидно, 0
К данному разряду мер оценки локализации можно отнести и метрику Хаусдорфа:

Хотя классическая версия данной метрики обладает желательными для использования в оценке цифровых изображений топологическими свойствами, на практике она используется редко в силу своей высокой чувствительности к шуму и даже к изменениям в один пиксель на оцениваемом изображении. В свою очередь, метрика Пратта наиболее часто используемая.
Недостатком перечисленных мер оценки локализации является то, что они зачастую нечувствительны к ошибкам второго рода. Например, если все ошибки оцениваемого образа B второго рода и BÎA, то значения e=e2=0, а FOM(A, B)= =n(B)/n(A)=1- . В отличие от метрики Пратта меры e и e2 сильно чувствительны к фоновому шуму. К примеру, если образ B содержит даже один пиксель x, находящийся на большом расстоянии от A, значение этого расстояния даст большой вклад в значение средних ошибок расстояния. Это согласуется с известным фактом из статистики о неустойчивости среднего арифметического. В силу того, что перечисленные меры
. В отличие от метрики Пратта меры e и e2 сильно чувствительны к фоновому шуму. К примеру, если образ B содержит даже один пиксель x, находящийся на большом расстоянии от A, значение этого расстояния даст большой вклад в значение средних ошибок расстояния. Это согласуется с известным фактом из статистики о неустойчивости среднего арифметического. В силу того, что перечисленные меры
оценки локализации нормируются на переменный множитель n(B) или max{n(A), n(B)}, возможны сложности с интерпретацией их значений (например, может быть не ясно, как интерпретировать значения FOM(A, B) для фиксированного A и различных B в ситуации, когда n(B)>n(A)). Ряд недостатков метрики Пратта был перечислен в работе [3]. В частности, при оценке данной метрикой результатов выделения границ лапласианом часто возникали ситуации высоких значений FOM на изображениях, содержащих участки разрывов границ (дырок) и участки, где получившийся граничный контур осциллирует вокруг своего истинного положения (на GT-изображении). Это наблюдение можно объяснить тем, что для xÎAÈB значение FOM(A, BÈx)k–1/2(FOM(A, B)–1–1)1/2. В ситуации, когда FOM(A,B)>0,9 и k=1/9, это приводит к соотношению FOM(A, BÈx)
 Также в работе [3] приведен получивший известность противоречащий здравому смыслу пример поведения метрики Пратта (так называемый пример Peli-Malah), показанный на рисунке 2.
Также в работе [3] приведен получивший известность противоречащий здравому смыслу пример поведения метрики Пратта (так называемый пример Peli-Malah), показанный на рисунке 2.
Авторами примера были предъявлены два изображения, приведенные на рисунке 2b, с, где значения FOM будут одинаковыми (в данном примере равными 0,941), если в качестве GT-образа взять квадрат размером 5´5 пикселей, изображенный на рисунке 2a. Значения вышеприведенных мер оценки качества детектирования будут также одинаковыми. Применительно к метрике Пратта подобные примеры означают, что она позволяет соответствовать нескольким выделенным граничным пикселям одному и тому же пикселю на GT-изображении (в случае отсутствия взаимно однозначного соответствия пикселей значение FOM может быть таким же, как и в случае наличия такого соответствия). В работе [3] предложена мера оценки локализации, представляющая собой Lp-модификацию метрики Хаусдорфа:

где в качестве w, как правило, берется так называемая функция отсечения: w(t)=min{t, c} для некоторого фиксированного c>0. Данная метрика, как и метрика Хаусдорфа, обладает желаемыми топологическими свойствами. При этом, в от- личие от последней, она более устойчива к возмущениям в один или несколько пикселей (максимум в разности расстояний заменяется на Lp среднее). Ряд экспериментов показал ее более адекватное поведение в сравнении с метрикой Пратта. Так, например, на рисунке 2b, с значения D2 при c=5 были 0,323 и 0,512 соответственно. В то же время метрика Пратта продемонстрировала более устойчивое поведение к малым возмущениям границы. В дальнейшем были предложены обобщения метрики Dp, позволяющие использовать ее для сравнения полутоновых изображений. Для оценки детекторов границ данная метрика используется сравнительно редко.
В силу того, что отсутствие взаимно однозначного соответствия между пикселями оцениваемой карты границ и соответствующим GT-изображением в перечисленных мерах может привести к их нереалистичным оценкам, представляется целесообразным использовать меры, где подразумевается такое соответствие. В частности, в работе [1] предложено проводить вычисление мер чувствительности и ошибки первого рода с использованием взаимно однозначного соответствия. А именно, берется дистанционный порог T (в работе он полагался равным 3). Если в окрестности T пиксель оцениваемой граничной карты оказывался без соответствующих GT-пикселей, значение ошибки первого рода увеличивалось на единицу. Если соответствующий GT-пиксель находился, значение чувствительности увеличивалось на единицу, и этот пиксель помечался как использованный, так что его нельзя было использовать в дальнейшем. Если в окрестности T оказывалось несколько GT-пикселей, в качестве соответствующего брался тот, который находился на кратчайшем расстоянии от пикселя оцениваемого изображения. В работе отмечалось, что предложенный метод слегка меняет значения ошибки первого рода и чувствительности по сравнению с их вычислением обычным способом. Однако он не влияет на общие результаты оценки производительности детекторов границ. В [4] данная методика модернизирована для работы с картами границ, содержащими информацию о силе края. Именно, если граничный пиксель имеет два соответствующих ему пикселя, находящихся на одинаковом расстоянии, из них выбирается наиболее сходный по силе края. Метрика, сравнивающая два изображения и построенная на данном соответствии, была названа в [4] метрикой кратчайшего пути (Closest Distance Metric, CDM). В свою очередь, в работе [4] была предложена альтернативная метрика, основанная на поиске соответствующих пикселей на сравниваемых изображениях, так называемая метрика соответствия пикселей (Pixel Correspondence Metric, PCM). Для каждой пары соответствующих пикселей строится функция затрат, вычисляемая с учетом расстояния между ними и силы края. Выбирается пара соответствующих пикселей с учетом наименьшего значения функции затрат. Общее значение метрики соответствия пикселей между изображениями f и g вычисляется по формуле  где
где  – стоимость оптимального соответствия между образами, вычисляемая как сумма значений функции затрат по парам соответствующих пикселей;
– стоимость оптимального соответствия между образами, вычисляемая как сумма значений функции затрат по парам соответствующих пикселей;  – общее число граничных пикселей в f и g. Индекс Т означает окрестность, в которой ищутся соответствующие пиксели. Поиск пар пикселей по минимальному значению функции затрат представляет собой трудоемкий вычислительный процесс. Для этого поиска используется алгоритм из теории двудольных графов, разработанный для решения сходной задачи. Данная метрика наряду с FOM и CDM использовалась для оценки нескольких зашумленных классических изображений, обработанных детектором Canny, и данных изображений без добавления шума, обработанных несколькими версиями этого детектора. Основной задачей было исследование поведения указанных мер оценки локализации при небольших сдвигах полученных границ относительно GT-образов. Эксперименты показали в целом более аккуратное поведение метрики PCM по сравнению с CDM и FOM. В частности, при увеличении окрестности T увеличивается значение PCM, что согласуется со здравым смыслом (в данной ситуации возрастает вероятность найти соответствующий пиксель с меньшим значением функции затрат). Однако явные преимущества метрики PCM над CDM выявлены не были, хотя программная реализация последней значительно проще.
– общее число граничных пикселей в f и g. Индекс Т означает окрестность, в которой ищутся соответствующие пиксели. Поиск пар пикселей по минимальному значению функции затрат представляет собой трудоемкий вычислительный процесс. Для этого поиска используется алгоритм из теории двудольных графов, разработанный для решения сходной задачи. Данная метрика наряду с FOM и CDM использовалась для оценки нескольких зашумленных классических изображений, обработанных детектором Canny, и данных изображений без добавления шума, обработанных несколькими версиями этого детектора. Основной задачей было исследование поведения указанных мер оценки локализации при небольших сдвигах полученных границ относительно GT-образов. Эксперименты показали в целом более аккуратное поведение метрики PCM по сравнению с CDM и FOM. В частности, при увеличении окрестности T увеличивается значение PCM, что согласуется со здравым смыслом (в данной ситуации возрастает вероятность найти соответствующий пиксель с меньшим значением функции затрат). Однако явные преимущества метрики PCM над CDM выявлены не были, хотя программная реализация последней значительно проще.
Следует отметить, что совместное применение нескольких мер различий из двух рассмотренных классов (статистических и мер оценки локализации) к оценке детекторов границ может поставить вопрос о согласованности их результатов и предпочтениях в их интерпретации. Например, в работе [2] для оценки шести детекторов границ, примененных к тестовым изображениям, подверженным аффинным преобразованиям (поворотам, сдвигам и растяжениям), использовались чувствительность, специфичность, а также метрики Пратта и Хаусдорфа. Результаты измерений показали существенно худшее поведение двух из рассматриваемых детекторов и невозможность выявить лидера из оставшихся четырех детекторов, опираясь исключительно на значения данных мер различий. Также было замечено, что в некоторых случаях выбор между результатами работы двух детекторов на одном тестовом образе осуществлялся на основании значений метрики Хаусдорфа, в то время как значения других метрик практически совпадали. Тем самым использование метрики Хаусдорфа в сочетании с другими метриками оказывалось полезным. В некоторых работах применяется комбинация одной из мер различий с метрикой, не использующей GT-образы. Можно сделать вывод, что на практике задача сочетания различных метрик не менее актуальна, чем задача совершенствования существующих различий.
Нечеткие методы оценки
В настоящее время разработано большое число алгоритмов обработки изображений, в той или иной степени использующих элементы теории нечетких множеств (например [5]). Во многих ситуациях выбор таких алгоритмов вполне оправдан. Как отмечалось выше, полутоновые изображения являются нечеткими по своей природе из-за неопределенности, существующей в локализации положения границы, отделяющей объект от фона. Особенно это характерно для размытых изображений. Следовательно, современные методы сравнительного исследования должны уметь работать с подобными алгоритмами, а также включать в себя элементы нечеткой логики.
Начиная с ранних работ, посвященных использованию нечеткой логики в задачах выделения границ, делались попытки оценить качество работы предлагаемых алгоритмов путем введения различного рода мер, характеризующих существо- вание, локализацию, связность выделенных гра- ничных пикселей. Следует, однако, признать, что методика сравнительного исследования четких и нечетких детекторов границ не получила достаточного развития. В ряде работ, посвященных анализу и классификации аэрокосмических снимков, было проведено обобщение нескольких известных статистических мер оценки качества на случай нечетких множеств, позволяющее в том числе сравнивать между собой четкие и нечеткие множества. Соответствующие меры были названы нечеткими мерами сходства. Там же рассматривалась и концепция нечеткого GT-образа. Результаты данных работ предназначались для определения на снимках областей лесов, воды, городской застройки и т.п., но они могут быть применены и для исследования производительности различных детекторов границ. Это наблюдение нашло свое отражение в работе [5], где несколько известных (четких) детекторов границ было протестировано с использованием нечетких мер сходства и нечетких GT-образов. Рассмотрим подробнее эти концепции. Приведем несколько основных понятий из теории нечетких множеств.
Пусть X – непустое множество (в данном случае растр изображения). Нечеткое множество C на X – это пара , где fC – отображение X на [0, 1]. Значение fC (x) в точке xÎX называется степенью принадлежности x множеству C, а функция fC – функцией принадлежности нечеткого множества. Обозначим множество всех нечетких множеств на X за [0, 1]X. Для A и B из [0, 1]X нечеткое отношение включения AÌB означает, что fA(x)≤fB(x) для всех xÎX.
Нечеткая мера сходства есть отображение s : [0, 1]X´[0, 1]X®[0,1], сопоставляющее множествам A, BÎ[0, 1]X степень сходства s(A, B)Î[0, 1] и удовлетворяющее условиям
· s(A, A)=1 для любого нечеткого A;
· s(A, B)=s(B, A) для всех нечетких A и B (коммутативность);
· s(A, C)≤min{s(A, B), s(B, C)} при AÌBÌС.
Важными примерами данных мер являются следующие:

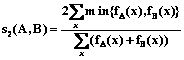 .
.
Заметим, что обычные (четкие) подмножества M из X включаются в данный подход, если рассматривать их как стандартные характеристические функции 1M : X®[0, 1]. Тем самым меры s1 и s2 можно применять, когда A или B или оба они являются четкими множествами. В частности, для четких A или B, отождествленных со своими характеристическими функциями, s1 и s2 совпадают с мерами оценки качества классификации Шорта и Хеллдена соответственно [5]. Изначально эти меры определялись только для четких множеств, так что меры s1 и s2 можно рассматривать как их обобщение.
Для нечетких GT-образов не существует общих правил построения. В работе [5] было сделано предположение, что их включение в системы сравнительного тестирования детекторов границ позволит не только тестировать нечеткие детекторы, но и сделать процедуру тестирования всех детекторов более содержательной. Там же предлагались различные нечеткие GT-образы, соответствующие одному и тому же тестовому изображению. Предполагалось, что они позволят лучше протестировать те или иные свойства исследуемого детектора границ. В качестве примера в [5] рассматривалось изображение исчезающий уступ (рис. 3a). На рисунке 3b изображен соответствующий GT-образ, построенный стандартным образом (с допустимой ошибкой локализации в 1 пиксель). На рисунке 3с, d изображены два нечетких GT-образа G1 и G2, соответствующих рисунку 3a. Их отличают различные функции m1 и m2 принадлежности пикселей множеству границ. Функция принадлежности m1 является прямоугольной, фактически образ G1 эквивалентен стандартному образу (рис. 3b). Функция принадлежности m2 учитывает относительную силу края граничных пикселей (рис. 3a), присваивая значение 1 наиболее сильным пикселям в нижней части середины данного рисунка. Тестирование двух детекторов (Smith и Heitger) с использованием данных изображений показало, что, поскольку функция m1 присваивает одинаковые значения (равные 1) сильным и слабым пикселям, ее уместно использовать для проверки способности детектора выделять слабые края. В то же время значения m2 для граничных пикселей зависят от их расположения (и силы), тем самым делая значения соответствующих нечетких мер сходства чувствительными к разрывам (дыркам) на карте границ, выделенной детектором. Соответственно, образ G2 предпочтительнее использовать для проверки свойства выделять непрерывные границы.
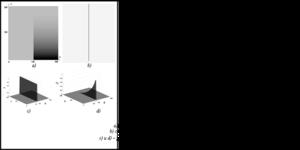 Другим потенциально важным приложением нечетких GT-образов из [5] является возможность их использования в проверке свойства детектора границ выделять граничные точки, существенные для характеризации ограничиваемого объекта. Например, для прямоугольника таковыми являются угловые точки. Задавая для них более высокие значения функции принадлежности множеству границ в сравнении с остальными граничными точками GT-образа, можно добиться высокой чувствительности нечетких мер сходства к выделению этих существенных точек. Однако в рабо- те [5] нет методики построения таких образов и использования различных нечетких мер сходства для практического тестирования детекторов границ. Так что, вопрос о создании методологии тестирования данных алгоритмов с использованием нечетких элементов остается открытым.
Другим потенциально важным приложением нечетких GT-образов из [5] является возможность их использования в проверке свойства детектора границ выделять граничные точки, существенные для характеризации ограничиваемого объекта. Например, для прямоугольника таковыми являются угловые точки. Задавая для них более высокие значения функции принадлежности множеству границ в сравнении с остальными граничными точками GT-образа, можно добиться высокой чувствительности нечетких мер сходства к выделению этих существенных точек. Однако в рабо- те [5] нет методики построения таких образов и использования различных нечетких мер сходства для практического тестирования детекторов границ. Так что, вопрос о создании методологии тестирования данных алгоритмов с использованием нечетких элементов остается открытым.
В заключение необходимо отметить, что в последние двадцать лет существенно вырос интерес к сравнительному исследованию алгоритмов обработки изображений, хотя достижения в этой области пока отстают от сегодняшних потребностей. Каждый из рассмотренных подходов имеет свои достоинства и недостатки и, как следствие, ограничения в применении. Тем не менее, накопленные результаты позволяют дать подробную характеристику известным детекторам границ. Эта информация оказывается полезной практическим пользователям при выборе того или иного детектора границ для решения своих задач.
Кроме того, можно сделать вывод, что для пользователя, решающего проблему выбора одного из нескольких имеющихся детекторов границ, в числе наиболее перспективных представляется путь их сравнительного тестирования с использованием GT-оценок. Следует заметить, что более современные версии мер различий имеют сомнительные преимущества над более ранними, к тому же численная реализация новых версий зачастую достаточно сложна.
По мнению авторов, выработка методологии совместного использования известных мер для сравнительного тестирования детекторов границ является перспективной задачей. Например, пользуясь результатами [2], можно рассмотреть задачу определения ситуаций, в которых использование метрики Хаусдорфа совместно с метриками Пратта и среднеквадратичной делает тестирование более качественным. Кроме того, полезно сочетание мер различных классов, оценивающих качество детектирования и локализации.
Рассмотренный нечеткий подход к оценке детекторов границ позволяет проводить углубленное тестирование детекторов границ, как использующих элементы теории нечетких множеств, так и не использующих данную теорию.
Литература
1. Bowyer K.W., Kranenburg C., Dougherty S. Edge detector evaluation using empirical ROC curves, Computer vision and Image Understanding. 2001. Vol. 84. №. 1, pp. 77–103.
2. Gribkov I.V. [et al.]. Edge Detection under Affine Transformations: Comparative Study by PICASSO 2 System, WSEAS Transactions on Signal Processing. 2006. Is. 9. Vol. 2, pp. 1215–1221.
3. Baddeley A.J. Errors in binary images and Lp version of the Hausdorff Metric, Nieuw Archief voor Wiskunde. 1992. Vol. 10, pp. 157–183.
4. Prieto M.S., Allen A.R. A similarity metric for edge images, IEEE Trans. Pattern Anal. Mach. Intell. 2003. Vol. 25. № 10, pp. 1265–1273.
5. Osipov A. A fuzzy approach to performance evaluation of edge detectors, in Lecture Notes in Signal Science, Internet and Education, WSEAS Press. 2007, pp. 94–99.





 где n(·) – число пикселей в соответствующем множестве, то есть как отношение неправильно выделенных граничных пикселей к общему числу пикселей, не являющихся граничными.
где n(·) – число пикселей в соответствующем множестве, то есть как отношение неправильно выделенных граничных пикселей к общему числу пикселей, не являющихся граничными. то есть как отношение невыделенных граничных пикселей к общему числу граничных пикселей.
то есть как отношение невыделенных граничных пикселей к общему числу граничных пикселей. где D – симметрическая разность множеств.
где D – симметрическая разность множеств.
 , то есть отношение правильно выделенных граничных пикселей к общему числу граничных пикселей, а также специфичность (Specificity):
, то есть отношение правильно выделенных граничных пикселей к общему числу граничных пикселей, а также специфичность (Specificity):  .
.
 , где f(x) – величина яркости изображения f в точке x. В случае детекторов границ f и g могут принимать значения 0 или 1 в зависимости от того, является ли точка соответствующего изображения граничной или нет. Сюда же относятся эквивалентные (в данной ситуации) отношения сигнала к шуму, пиковое и среднеквадратическое. Эти отношения используются и на этапе предобработки изображений (перед выделением границ) для оценки соответствующих фильтров.
, где f(x) – величина яркости изображения f в точке x. В случае детекторов границ f и g могут принимать значения 0 или 1 в зависимости от того, является ли точка соответствующего изображения граничной или нет. Сюда же относятся эквивалентные (в данной ситуации) отношения сигнала к шуму, пиковое и среднеквадратическое. Эти отношения используются и на этапе предобработки изображений (перед выделением границ) для оценки соответствующих фильтров.
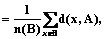 где d(X,A)=inf r(x, a), aÎA, а
где d(X,A)=inf r(x, a), aÎA, а  в рассматриваемой дискретной ситуации представляет собой метрику кратчайшего пути [3]. Сюда же относятся среднеквадратическая ошибка расстояния:
в рассматриваемой дискретной ситуации представляет собой метрику кратчайшего пути [3]. Сюда же относятся среднеквадратическая ошибка расстояния:  а также часто встречающаяся в литературе метрика Пратта
а также часто встречающаяся в литературе метрика Пратта  где k – коэффициент масштабирования, обычно полагаемый равным 1/9, а метрика кратчайшего пути нормируется таким образом, что наименьшее ненулевое расстояние между соседними пикселями равно единице. Заметим, что FOM(A, B)¹ ¹FOM(B, A), очевидно, 0
где k – коэффициент масштабирования, обычно полагаемый равным 1/9, а метрика кратчайшего пути нормируется таким образом, что наименьшее ненулевое расстояние между соседними пикселями равно единице. Заметим, что FOM(A, B)¹ ¹FOM(B, A), очевидно, 0
 . В отличие от метрики Пратта меры e и e2 сильно чувствительны к фоновому шуму. К примеру, если образ B содержит даже один пиксель x, находящийся на большом расстоянии от A, значение этого расстояния даст большой вклад в значение средних ошибок расстояния. Это согласуется с известным фактом из статистики о неустойчивости среднего арифметического. В силу того, что перечисленные меры
. В отличие от метрики Пратта меры e и e2 сильно чувствительны к фоновому шуму. К примеру, если образ B содержит даже один пиксель x, находящийся на большом расстоянии от A, значение этого расстояния даст большой вклад в значение средних ошибок расстояния. Это согласуется с известным фактом из статистики о неустойчивости среднего арифметического. В силу того, что перечисленные меры

 где
где  – стоимость оптимального соответствия между образами, вычисляемая как сумма значений функции затрат по парам соответствующих пикселей;
– стоимость оптимального соответствия между образами, вычисляемая как сумма значений функции затрат по парам соответствующих пикселей;  – общее число граничных пикселей в f и g. Индекс Т означает окрестность, в которой ищутся соответствующие пиксели. Поиск пар пикселей по минимальному значению функции затрат представляет собой трудоемкий вычислительный процесс. Для этого поиска используется алгоритм из теории двудольных графов, разработанный для решения сходной задачи. Данная метрика наряду с FOM и CDM использовалась для оценки нескольких зашумленных классических изображений, обработанных детектором Canny, и данных изображений без добавления шума, обработанных несколькими версиями этого детектора. Основной задачей было исследование поведения указанных мер оценки локализации при небольших сдвигах полученных границ относительно GT-образов. Эксперименты показали в целом более аккуратное поведение метрики PCM по сравнению с CDM и FOM. В частности, при увеличении окрестности T увеличивается значение PCM, что согласуется со здравым смыслом (в данной ситуации возрастает вероятность найти соответствующий пиксель с меньшим значением функции затрат). Однако явные преимущества метрики PCM над CDM выявлены не были, хотя программная реализация последней значительно проще.
– общее число граничных пикселей в f и g. Индекс Т означает окрестность, в которой ищутся соответствующие пиксели. Поиск пар пикселей по минимальному значению функции затрат представляет собой трудоемкий вычислительный процесс. Для этого поиска используется алгоритм из теории двудольных графов, разработанный для решения сходной задачи. Данная метрика наряду с FOM и CDM использовалась для оценки нескольких зашумленных классических изображений, обработанных детектором Canny, и данных изображений без добавления шума, обработанных несколькими версиями этого детектора. Основной задачей было исследование поведения указанных мер оценки локализации при небольших сдвигах полученных границ относительно GT-образов. Эксперименты показали в целом более аккуратное поведение метрики PCM по сравнению с CDM и FOM. В частности, при увеличении окрестности T увеличивается значение PCM, что согласуется со здравым смыслом (в данной ситуации возрастает вероятность найти соответствующий пиксель с меньшим значением функции затрат). Однако явные преимущества метрики PCM над CDM выявлены не были, хотя программная реализация последней значительно проще.
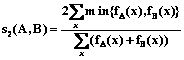 .
.
