Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Процессная семантика языков распределенного программирования
Аннотация:В данной статье семантика языков распределенного программирования исследуется посредством сопоставления программам множества вычислительных последовательностей и анализа семантических значений, которые могут быть представлены системами рекурсивных уравнений. Это позволяет проводить формальную верификацию программ.
Abstract:In this article the semantics of distributed programming languages researched by comparing programs a set of computational sequence and analysis of the semantic values thet can be represented by systems of recursive equations. It can detect deadlocks and locks in distributed program, loops, verify accessibility, to prove the equivalence (may, must, observational) of programs and branches.
| Авторы: Кораблин Ю.П. (y.p.k@mail.ru) - Российский государственный социальный университет, г. Москва (профессор), Москва, Россия, доктор технических наук, Кучугуров И.В. (tws13@mail.ru) - Российский государственный социальный университет, г. Москва | |
| Ключевые слова: эквивалентность, эквациональная характеризация, семантические равенства, априорная семантика, алгебраическая семантика, процессная семантика, верификация |
|
| Keywords: equivalence, equational characterization, semantic equality, semantic equality, algebraic semantics, process semantics, verification |
|
| Количество просмотров: 14409 |
Версия для печати Выпуск в формате PDF (5.83Мб) Скачать обложку в формате PDF (1.28Мб) |
С развитием распределенных систем и параллельной обработки информации остро встает задача создания качественного ПО. Исследуем семантику языков распределенного программирования посредством сопоставления программам (схемам программ) множества вычислительных последовательностей (ВП) и анализа семантических значений в заданной алгебраической модели ВП. Под ВП будем понимать последовательность выполнения действий (команд и тестов) программы. В качестве модели языка распределенного программирования рассмотрим язык L, имеющий элементарные команды, последовательную и параллельную композицию, недетерминированный выбор, синхронизацию и взаимодействие посредством передачи сообщений и итерацию. Такой тип языка может рассматриваться как ядро для построения различных языков параллельного программирования, использующих данную модель взаимодействия и синхронизации между компонентами программы. В основе рассматриваемого подхода к семантике распределенных программ лежат следующие принципы. Во-первых, с учетом разнообразия языков и их применений семантические области задаются посредством композиции блоков, описывающих различные свойства семантических объектов. Во-вторых, для описания семантики таких программ в определение семантической функции вводится параметр, задающий среду вычисления, так как использование операции параллельной композиции в семантической области требует определения этой операции и ее свойств. В-третьих, допущение как конечных, так и бесконечных вычислений, определяемых программой в используемом языке, требует строгого математического подхода для спецификации этих вычислений. При описании семантических областей и доказательстве корректности семантических функций используется аппарат метрической топологии. Синтаксис языка L Предположим, что заданными являются множества: элементарных команд Типичные элементы множеств могут допускать индексацию. Кроме того, выделим еще три константы: Множество команд
где
Фигурные скобки используются в БНФ для обозначения нулевого либо большего количества повторений конструкции, заключенной в скобки. Через Алгебраическая семантика: математические основы и семантические равенства Семантическая функция сопоставляет программе в языке Полагая, что любая программа может, в свою очередь, быть компонентом другой программы, в результате композиции семантических значений компонентов некоторой программы всегда получится априорная семантика всей программы. При этом, если в семантическом значении компонента программы могут присутствовать вычислительные пути, содержащие команды ввода/вывода, означающие возможное взаимодействие с другими компонентами, то в семантическом значении всей программы целиком все такие команды должны быть реализованы путем взаимодействия с соответствующим удалением ВП, начинающихся с этих команд. При задании семантики необходимо учитывать, что в языке 1) 2) Индекс у команды ввода/вывода указывает на процесс, с которым может осуществляться взаимодействие. В первой программе имеет место случай локального недетерминизма, то есть выбор альтернатив для выполнения в процессе 1 не зависит от других процессов. В случае выбора второй альтернативы для выполнения оба процесса программы будут взаимно заблокированы. Во второй программе успешное завершение гарантируется вследствие разрешения недетерминизма на уровне программы (глобального недетерминизма). Здесь решение вопроса о выборе альтернативы переносится на уровень параллельной композиции двух процессов, тогда как на уровне каждого процесса в отдельности имеется лишь априорная готовность к взаимодействию команд ввода/вывода. Еще одним параметром, влияющим на семантическое значение программы, является механизм управления завершением циклов, использующих глобальный недетерминизм. Циклы завершаются тогда, когда значения всех защит, определяющих возможность выполнения альтернатив цикла, являются ложными. Циклические команды, в которых в качестве защиты используются команды ввода/вывода, завершаются, если завершились все процессы, с которыми могут взаимодействовать эти команды. Очевидно, что анализ завершения таких циклов также возможен только на глобальном уровне. Семантические области. Предположим, что задаются множества значений элементарных команд Типичные элементы семантических областей могут иметь индексы. Определим множество вычислительных последовательностей
Заметим, что одни и те же элементы Обозначим через Введем множество Определение 1. ВП Бесконечную последовательность вида Определение 2. Определим теперь
В последнем определении символ Априорная семантика. Априорную семантику процессов зададим как Семантическая функция рассчитывается следующим образом: 1) 2) 3) 4) 5) где функция 6) 7) 8) 9) 10) 11) 12) 13) 14) Заметим, что для обозначения операции параллельной композиции над семантическими значениями используется тот же символ, что и для параллельной композиции в языке Определим теперь семантическую функцию для выражений 1) 2) 3) Заметим, что в записи Перейдем к формальному определению функции среды Определение 3. Процесс Определение 4 (правило дедукции). Пусть метка 1) если 2) если 3) если, в свою очередь, gc Определение 5. Пусть метка В общем случае понятие «родительский» можно обобщить, полагая, что, если метка Определение 6. Родословной n-го порядка Определение 7. Родословной компонента Заметим, что порождение родительской метки 1-го порядка для любого компонента Определение 8. Пусть Очевидно, что, если множество Лемма 1. Пусть Доказательство. Тривиально, из определений 7 и 8. Лемму 1 можно обобщить на любое конечное число компонентов программы. Для упрощения процесса нахождения среды вычисления компонентов Лемма 2. а) б) в) г) д) Доказательство. Тривиально, из определений 4, 8. Пусть Лемма 3. Пусть Доказательство. Тривиально, методом численной индукции. Пример 1. Пусть дана программа
и пусть Вводя порядок
Таким образом, получена фиксированная точка, а следовательно, Строго говоря, для того чтобы минимальная фиксированная точка оператора Таким образом, введенные выше определения родословной для компонента программы и подмножества компонентов являются корректными. Исследуем подробнее семантическую область Свойства операции над элементами семантической области опишем системой аксиом (схем аксиом) и правил вывода. Систему аксиом зададим как набор блоков, каждый из которых описывает определенные свойства семантических объектов. Аксиоматизация свойств семантической области. Для обозначения элементов семантической области используем метапеременные Аксиомы, задающие базисные свойства операций (A1) (A2) (A3) (A4) (A5) (A6) (A7) (A8) (A9) (A10) (A11) (A12) (A13) Для описания свойств параллельной композиции
Из этого определения следует: если хотя бы один из аргументов функции Функция Операцию (Р1) (Р2) Таким образом, определенная операция параллельной композиции является ассоциативной (Р2). Кроме того, в дальнейшем из коммутативности операции Операция (С1) (С2) (С3)
(С4) (С5)
(С6) (С7) (С8) (С9) Операция (F1) (F2) (F3) (F4) (F5) (F6) (F7) Отметим, что формально аксиомы С8 и F4 не являются независимыми и могут быть выведены из аксиомы А6, однако для характеризации свойств операций Введем также операции абстракции ( Для произвольного (AB1) (AB2) (AB3) (AB4) (AB5) (AB6) (E1) (E2) (E3) (E4) (E5) (E6) Введем также в предлагаемую формальную систему правило замены. (СН) Пусть Теорема 1. Формальная система, состоящая из блоков А1 Доказательство. Тривиально, путем непосредственной проверки того факта, что, если некоторая ВП принадлежит левой части какой-либо аксиомы, то она принадлежит и правой части, и наоборот. Непосредственно проверяется и правило вывода СН. Эквациональная характеризация семантических значений Предложенный подход позволяет описывать ВП, соответствующие всем возможным вычислениям программы. В то же время непосредственный анализ полученных семантических значений программ на возможность появления исключительных ситуаций является затруднительным. Покажем, что для любого элемента Прежде чем определить систему уравнений, введем несколько вспомогательных определений. Определение 9. Пусть
Заметим, что для выражения Определение 10. Множество ВП
где
где При записи уравнений вида Рассмотрим пример представления семантического значения в языке Пример 2: В соответствии с семантическим определением имеем
где Опуская Аналогично предыдущему получаем
Таким образом, имеем Представим
Далее получаем
Данная система уравнений задает множество ВП, сопоставляемое программе Для получения же семантического значения программы
Таким образом, выводим следующую систему уравнений:
Наличие Теорема 2. Каждое множество ВП Доказательство. Методом индукции по структуре P. Базис. Для Индуктивный шаг. Пусть По предположению индукции существуют множества
1.
Запишем
Применяя аксиомы А4, А2, А5 и А11, получаем
Если Применяя далее аксиомы А1, А2, А3 и А5, получим
где все выражения 2. 3.
Запишем
Используя аксиомы А1, А2, А3, получим 4.
Запишем
Применяя аксиому Р1, а затем аксиомы
Если
где все 5.
Количество выражений (4) конечно. По индуктивному предположению имеем
Поскольку по определению имеем, что
то, подставляя
Отсюда получаем следующее свойство для фиксированной точки Используя это свойство, имеем Применяя аксиомы А4, А5 и А11, получим
+
где все Для
Используя аксиомы А4, А5, А6, А8, А11, получаем
Рассмотрим последнее слагаемое Если сумма Применяя вновь аксиому А4, получим
где все Таким образом, получаем, что Программная реализация В соответствии с изложенной теорией авторами была создана программа, которая по тексту входной программы на языке
будут построены семантическое значение
и соответствующая система рекурсивных уравнений:
Таким образом, в работе предложен метод задания процессной семантики схем распределенных программ и показано, что сопоставляемые программам семантические значения могут быть представлены системами рекурсивных уравнений. Это дает возможность решить ряд как теоретических, так и практических задач. Разработанная программа представления семантических значений в виде систем рекурсивных уравнений существенно упрощает и автоматизирует процесс анализа семантических значений распределенных программ. Литература 1. Кораблин Ю.П. Семантика языков распределенного программирования. М.: Изд-во МЭИ, 1996. 102 с. 2. Кораблин Ю.П. Семантика языков программирования. М.: Изд-во МЭИ, 1992. 102 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2913&page=article |
Версия для печати Выпуск в формате PDF (5.83Мб) Скачать обложку в формате PDF (1.28Мб) |
| Статья опубликована в выпуске журнала № 4 за 2011 год. [ на стр. 57 – 64 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Вопросы эквивалентности схем параллельных программ
- Разработка инструментов верификации драйверов на основе семантических моделей
- Синтезирование программ на основе описания графоаналитической модели
- Общая схема верификации утверждений Р-логики с неизвестными параметрами
- Верификация моделей систем на базе эквациональной характеристики формул CTL
Назад, к списку статей



 с типичным элементом
с типичным элементом  ; булевских выражений
; булевских выражений  с типичным элементом
с типичным элементом  ; команд ввода
; команд ввода  с типичным элементом
с типичным элементом  ; команд вывода
; команд вывода  с типичным элементом
с типичным элементом  ; меток процессов
; меток процессов  с типичными элементами
с типичными элементами 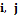 , где
, где 
 – пустая команда;
– пустая команда;  и
и  – тождественно истинное и тождественно ложное булевские значения.
– тождественно истинное и тождественно ложное булевские значения. с типичным элементом
с типичным элементом  определим следующим образом:
определим следующим образом: ,
, – типичный элемент множества защищенных команд
– типичный элемент множества защищенных команд  со следующим синтаксисом:
со следующим синтаксисом: ,
, ,
, .
. обозначается типичный элемент множества защит
обозначается типичный элемент множества защит  , а через
, а через 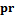 – типичный элемент множества процессов
– типичный элемент множества процессов  . В дальнейшем круглые скобки в записи
. В дальнейшем круглые скобки в записи  опускаются там, где это не вызывает недоразумений.
опускаются там, где это не вызывает недоразумений. множество вычислительных последовательностей (путей), по которым может выполняться данная программа. Для построения семантики распределенной программы используем принцип построения семантического значения всей программы на основе семантических значений компонентов этой программы. Семантическое значение компонента, рассматриваемое вне программной среды, называется априорной семантикой компонента программы.
множество вычислительных последовательностей (путей), по которым может выполняться данная программа. Для построения семантики распределенной программы используем принцип построения семантического значения всей программы на основе семантических значений компонентов этой программы. Семантическое значение компонента, рассматриваемое вне программной среды, называется априорной семантикой компонента программы. ;
; .
. с типичным элементом
с типичным элементом  ; булевских выражений
; булевских выражений  с типичным элементом
с типичным элементом  ; команд ввода
; команд ввода 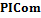 с типичным элементом
с типичным элементом  ; а также команд вывода
; а также команд вывода  с типичным элементом
с типичным элементом  ; взаимодействий
; взаимодействий  с типичным элементом
с типичным элементом 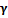 и множество
и множество  , содержащее константы
, содержащее константы  (тождественное преобразование),
(тождественное преобразование),  (останов),
(останов),  (тождественно-истинное значение) и
(тождественно-истинное значение) и  (тождественно-ложное значение).
(тождественно-ложное значение). с типичным элементом
с типичным элементом  . Предварительно определим два дополнительных множества: множество тестов
. Предварительно определим два дополнительных множества: множество тестов  с типичным элементом
с типичным элементом  и множество действий
и множество действий  с типичным элементом
с типичным элементом  .
.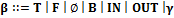 ;
; ;
; .
. могут использоваться в качестве и тестов, являющихся значениями защит команд, и действий, являющихся значениями команд. Элемент
могут использоваться в качестве и тестов, являющихся значениями защит команд, и действий, являющихся значениями команд. Элемент  конечную ВП, а через
конечную ВП, а через  – бесконечную.
– бесконечную. с типичным элементом
с типичным элементом  , то есть
, то есть  – это множество всех подмножеств множества
– это множество всех подмножеств множества  , последовательной композиции
, последовательной композиции  , параллельной композиции
, параллельной композиции  , теоретико-множественного вычитания
, теоретико-множественного вычитания  и минимальной фиксированной точки
и минимальной фиксированной точки  . Прежде чем определить значение
. Прежде чем определить значение  , введем два вспомогательных определения.
, введем два вспомогательных определения.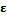 , если
, если  ;
;  .
. обозначим через
обозначим через  (зацикливание).
(зацикливание).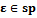 , если
, если  ;
; 
 и
и  или
или  ;
;  и
и  , то есть
, то есть  , где
, где  ,
,

 обозначает выражение, значение которого зависит от среды вычисления
обозначает выражение, значение которого зависит от среды вычисления  , где
, где  – множество функций вида
– множество функций вида  с типичным элементом
с типичным элементом  . Через
. Через  обозначено множество компонентов программы, определяемое как
обозначено множество компонентов программы, определяемое как  с типичным элементом
с типичным элементом  . Функция
. Функция  компонентов программы. Множество
компонентов программы. Множество  отличается от ранее введенного множества
отличается от ранее введенного множества  , имеют дополнительный параметр
, имеют дополнительный параметр  , характеризующий среду вычисления элемента
, характеризующий среду вычисления элемента  ,
, ,
, ,
, ,
, ,
, определяет семантические значения выражений,
определяет семантические значения выражений, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
. ;
;  .
. ,
, ,
,
 (либо
(либо  ) среда
) среда  (соответственно
(соответственно 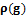 ) будут в общем случае различными.
) будут в общем случае различными. называется помеченным меткой
называется помеченным меткой  . При этом метка
. При этом метка  .
. либо
либо  , то метка
, то метка  и
и  ;
; либо
либо , то метка
, то метка  либо
либо  , то метка
, то метка  и
и  является родительской для процесса
является родительской для процесса  для некоторого вхождения компонента
для некоторого вхождения компонента  является минимальная фиксированная точка оператора
является минимальная фиксированная точка оператора 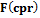 , то есть
, то есть  , где
, где  где
где  – родительская метка 1-го порядка компонента
– родительская метка 1-го порядка компонента  – функция вида
– функция вида 
 , порождающая для любого множества меток программы
, порождающая для любого множества меток программы  множество их родительских меток
множество их родительских меток  .
. 5.
5. есть множество всех компонентов некоторой программы
есть множество всех компонентов некоторой программы  , сопоставляющая каждому подмножеству компонентов
, сопоставляющая каждому подмножеству компонентов  программы множество меток, являющихся объединением родословных всех компонентов
программы множество меток, являющихся объединением родословных всех компонентов 
 .
. и
и  – компоненты программы
– компоненты программы 
 .
.




 следующим образом:
следующим образом:  где
где  , а функция
, а функция  – подмножество компонентов программы
– подмножество компонентов программы  Тогда
Тогда  .
.




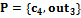 .
. на множестве
на множестве  как отношение включения множеств и обозначая пустое множество меток
как отношение включения множеств и обозначая пустое множество меток  через
через  ,
, ,
, ,
,
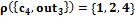 .
. и
и  монотонны. Из монотонности этих операций и конечности областей, на которых эти операции определены (в силу конечности программы
монотонны. Из монотонности этих операций и конечности областей, на которых эти операции определены (в силу конечности программы  и операции над элементами этой области. Обозначим через
и операции над элементами этой области. Обозначим через  множество
множество  с типичным элементом
с типичным элементом  . В дальнейшем используем как параметризованные, так и непараметризованные семантические области, полагая в последнем случае, что с каждым элементом непараметризованной области всегда может быть ассоциирован параметр
. В дальнейшем используем как параметризованные, так и непараметризованные семантические области, полагая в последнем случае, что с каждым элементом непараметризованной области всегда может быть ассоциирован параметр  , задающий среду вычисления соответствующего элемента. В тех случаях, когда параметризация является принципиальной при построении семантического значения, параметры будут задаваться явным образом (например, в элементах
, задающий среду вычисления соответствующего элемента. В тех случаях, когда параметризация является принципиальной при построении семантического значения, параметры будут задаваться явным образом (например, в элементах 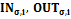 ), тогда как в других случаях, для упрощения записи, часто будем опускать параметр
), тогда как в других случаях, для упрощения записи, часто будем опускать параметр  у элементов области
у элементов области  .
. и
и  :
: ,
,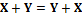 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
. используем операции
используем операции  и
и 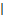 . Выражение
. Выражение  означает то же самое, что и
означает то же самое, что и  , за исключением того, что первым шагом будет действие из
, за исключением того, что первым шагом будет действие из  . Для определения операции
. Для определения операции  . Частично определенную функцию
. Частично определенную функцию  зададим следующим образом:
зададим следующим образом:
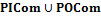 либо оба аргумента принадлежат одной из областей
либо оба аргумента принадлежат одной из областей  . Кроме того, взаимодействие
. Кроме того, взаимодействие  и
и 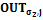 возможно лишь в том случае, если
возможно лишь в том случае, если  , а
, а  , то есть исходные команды
, то есть исходные команды  и
и  , значениями которых являются
, значениями которых являются  ,
,  .
. определим следующими аксиомами:
определим следующими аксиомами: ,
, .
. и
и  ,
, ,
,
 ,
, ,
,
 ,
, ,
, ,
, ,
, .
. ,
, ,
, ,
, ,
, ,
, ,
, .
. ) и инкапсуляции (
) и инкапсуляции ( ), где
), где  – множество, параметризующее эти операции. Операции
– множество, параметризующее эти операции. Операции  и имеют вид
и имеют вид  .
. , где
, где 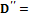
 , операции
, операции  ,
, ,
, ,
, ,
, ,
, ;
; ,
, ,
, ,
, ,
, ,
, .
. входит в
входит в  и
и  . Тогда, если
. Тогда, если  получено из
получено из  , то
, то  .
. существует представление его в виде конечной системы рекурсивных уравнений.
существует представление его в виде конечной системы рекурсивных уравнений. и
и  и
и 
 . Частичные функции
. Частичные функции  и
и  определяются следующей таблицей:
определяются следующей таблицей:
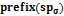



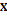





 понятия префикса и суффикса не определяются, поскольку
понятия префикса и суффикса не определяются, поскольку  эквационально характеризуемо, если имеется конечное множество
эквационально характеризуемо, если имеется конечное множество  , таких, что
, таких, что  и для любого
и для любого  :
: ,
, 
 ,
,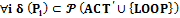 ,
, ,
,  , что
, что  , и
, и  , что
, что  .
.
 спользуем нотацию
спользуем нотацию  для суммы
для суммы  , где
, где  . Запись
. Запись  .
.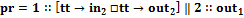 .
. , где
, где  ,
,  .
.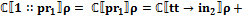

 ,
, .
. эквивалентны, получим
эквивалентны, получим  .
. .
.
 .
.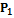 . Тогда
. Тогда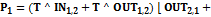










 +
+ ,
,

 =
= .
.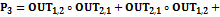

 ,
, ,
, ,
, ,
,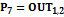 .
. , в которую программа
, в которую программа  и
и  , входящие в ВП априорного семантического значения
, входящие в ВП априорного семантического значения  и
и  , входящими в
, входящими в  , получим
, получим
 ,
, ,
,
 ,
, ,
,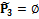 .
.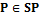 , сопоставляемое программе
, сопоставляемое программе  , где
, где  , эквациональная характеризация вытекает тривиально.
, эквациональная характеризация вытекает тривиально. и
и  будут эквационально характеризуемы. Тогда необходимо доказать, что
будут эквационально характеризуемы. Тогда необходимо доказать, что  и
и  эквационально характеризуемы.
эквационально характеризуемы. и
и  , такие, что
, такие, что  и
и



 . Обозначим
. Обозначим
 .
. вместо
вместо  . Количество выражений (1) конечно. По индуктивному предположению имеем
. Количество выражений (1) конечно. По индуктивному предположению имеем


 .
.



 .
.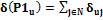 , где
, где  , то применим еще раз аксиому А4, заменяя в
, то применим еще раз аксиому А4, заменяя в  слагаемое
слагаемое  выражением
выражением  , причем, если
, причем, если  , то
, то  заменяем его представлением для
заменяем его представлением для  из
из 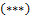 .
.

 входят в (1). Поскольку
входят в (1). Поскольку  , получаем, что
, получаем, что  . Тривиальный случай. Тогда к конечной системе уравнений для
. Тривиальный случай. Тогда к конечной системе уравнений для добавляется лишь одно уравнение:
добавляется лишь одно уравнение:  , откуда следует эквациональная характеризуемость выражения
, откуда следует эквациональная характеризуемость выражения  . Обозначим
. Обозначим (2)
(2) .
. вместо
вместо  и
и  вместо
вместо  . Количество выражений (2) конечно. По индуктивному предположению имеем
. Количество выражений (2) конечно. По индуктивному предположению имеем


 , где все выражения
, где все выражения  и
и  входят в (2). Поскольку
входят в (2). Поскольку  , получаем, что
, получаем, что  эквационально характеризуемо.
эквационально характеризуемо. . Обозначим
. Обозначим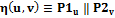 (3)
(3) .
. вместо
вместо  вместо
вместо 
 .
. , получим:
, получим:




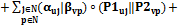





 .
. и
и  , то, применяя аксиомы С7, С9, А4, А5, а затем аксиомы
, то, применяя аксиомы С7, С9, А4, А5, а затем аксиомы  , получим
, получим
 и
и  входят в (3). Поскольку
входят в (3). Поскольку 
 , получаем, что
, получаем, что 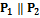 эквационально характеризуемо.
эквационально характеризуемо.


 .
. .
. , где
, где
 в оператор F(P1), имеем
в оператор F(P1), имеем

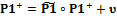 .
.
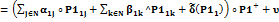 , где
, где 
 .
.

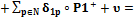
 (5)
(5) входят в (4), а
входят в (4), а  , поскольку
, поскольку  может принимать лишь одно из трех значений:
может принимать лишь одно из трех значений:  что соответствует определению
что соответствует определению  по индуктивному предположению имеем
по индуктивному предположению имеем 




 .
. .
. содержит
содержит 
 ,
, ,
,  входят в (4).
входят в (4).




 .
.