Во многих приложениях, связанных с проек- тированием многопроцессорных систем (МС), вычислительных комплексов, системного и прикладного ПО [1–2], оптимальной организации параллельных вычислительных процессов, значительный интерес представляют задачи, в которых множество конкурирующих процессов могут использовать не одну, а несколько копий структурированного программного ресурса (ПР). Случай, когда в общей памяти МС имеется одна копия ПР, с различных точек зрения описан в работах [3–5]. При этом были решены задачи нахождения минимального общего времени выполнения распределенных конкурирующих процессов, использующих структурированный на блоки ПР в различных режимах взаимодействия процессов, процессоров и блоков, получены критерии эффективности и оптимальности структурирования ПР, проведен сравнительный анализ режимов взаимодействия процессов, процессоров и блоков, решен ряд оптимизационных задач по расчету числа процессов, минимального числа процессоров и др. Изучение этих и других задач, относящихся к оптимальной организации параллельных вычислений, приобретает особую актуальность, когда в общей памяти МС одновременно могут размещаться две или более копий (c) ПР. Такое обобщение носит принципиальный характер ввиду того, что отражает основные черты мультиконвейерной обработки, а также позволяет сравнить эффективность конвейерной и параллельной обработки.
В данной работе строится и исследуется математическая модель организации конкурирующих процессов, использующих ограниченное число копий ПР. При этом с помощью метода структурирования ПР на блоки с их последующей конвейеризацией по процессам и процессорам исследуются оптимальные временные характеристики такой организации.
Математическая модель распределенных вычислений при ограниченном числе копий ПР
Конструктивными элементами для построения математических моделей систем распределенных вычислений являются понятия процесса и ПР.
Процесс будем рассматривать как последовательность блоков (команд, процедур) Q1, Q2, …, Qs, для выполнения которых используется множество процессоров (процессорных узлов, обрабатывающих устройств, интеллектуальных клиентов). При этом процесс называется распределенным, если все блоки или часть из них обрабатываются разными процессорами [2]. Для ускорения процессы могут обрабатываться параллельно, взаимодействуя путем обмена информацией. Такие процессы называются кооперативными, или взаимодействующими.
Ресурсом являются любые объекты, которые используются для выполнения процесса. Реентерабельные (многократно используемые) – это ресурсы, одновременно используемые несколькими вычислительными процессами. Для параллельных систем характерна ситуация, когда одну и ту же последовательность блоков или ее часть необходимо выполнять многократно. Такую последовательность будем называть программным ресурсом, а множество соответствующих процессов – конкурирующими.
Математическая модель распределенной обработки конкурирующих взаимодействующих процессов при ограниченном числе копий ПР включает в себя: p процессоров МС (p³2), которые имеют доступ к общей памяти; n распределенных конкурирующих процессов (n³2); s блоков структурированного на блоки ПР (s³2); матрицу T=[tij],  ,
, 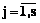 , времен выполнения блоков ПР распределенными взаимодействующими конкурирующими процессами; c копий (2£c£p) структурированного на блоки ПР, которые могут одновременно находиться в оперативной памяти, доступной для всех p процессоров, причем
, времен выполнения блоков ПР распределенными взаимодействующими конкурирующими процессами; c копий (2£c£p) структурированного на блоки ПР, которые могут одновременно находиться в оперативной памяти, доступной для всех p процессоров, причем  ; параметр e (e>0), характеризующий время дополнительных системных расходов, связанных с организацией конвейерного режима использования блоков структурированного ПР множеством взаимодействующих конкурирующих процессов при распределенной обработке.
; параметр e (e>0), характеризующий время дополнительных системных расходов, связанных с организацией конвейерного режима использования блоков структурированного ПР множеством взаимодействующих конкурирующих процессов при распределенной обработке.
Также предположим, что число процессов n кратно числу копий c структурированного ПР, то есть n=mc, m³2, и что взаимодействие процессов, процессоров и блоков ПР подчинено следующим условиям:
- ни один из процессоров одновременно не может обрабатывать более одного блока;
- процессы выполняются в параллельно-конвейерном режиме группами, то есть осуществляется одновременное (параллельное) выполнение c копий каждого блока в сочетании с конвейеризацией групп из c блоков по процессорам и процессам;
- обработка каждого блока ПР происходит без прерываний;
- распределение блоков ПР по процессорам для каждого из процессов i=lc+q,  , l³0,
, l³0, 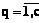 , осуществляется циклически по правилу: блок с номером
, осуществляется циклически по правилу: блок с номером  ,
, 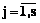 , k³0,
, k³0, 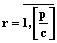 , распределяется на процессор с номером q+c(r–1).
, распределяется на процессор с номером q+c(r–1).
Введем следующие режимы взаимодействия процессов, процессоров и блоков с учетом наличия c копий ПР:
- асинхронный режим, при котором начало выполнения очередной группы из c копий блока Qj,  , определяется наличием c процессоров и готовностью этой группы блоков к выполнению (программный блок считается готовым к выполнению, если он не выполняется ни на одном из процессоров);
, определяется наличием c процессоров и готовностью этой группы блоков к выполнению (программный блок считается готовым к выполнению, если он не выполняется ни на одном из процессоров);
- первый синхронный режим, обеспечивающий линейный порядок выполнения блоков ПР внутри каждого из процессов без задержек, то есть для каждого процесса i=lc+q,  , l³0,
, l³0, 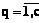 , момент завершения выполнения j-го блока на q+c(r–1)-м процессоре совпадает с моментом начала выполнения следующего (j+1)-го блока на (q+cr)-м процессоре,
, момент завершения выполнения j-го блока на q+c(r–1)-м процессоре совпадает с моментом начала выполнения следующего (j+1)-го блока на (q+cr)-м процессоре,  ,
, 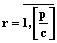 ;
;
- второй синхронный режим, при котором c копий каждого блока непрерывно переходят по группам из с процессов, то есть момент окончания обработки c копий текущего блока совпадает с моментом начала их обработки на следующей группе из c процессоров.
На рисунках 1–3 представлены диаграммы Ганта, иллюстрирующие выполнение n=4 распределенных конкурирующих процессов, использующих c=2 копии структурированного ПР в МС с p=7 процессорами в рассмотренных выше режимах и с заданной матрицей времени выполнения блоков ПР с учетом дополнительных системных расходов  .
.

Определение 1. Система n распределенных конкурирующих процессов называется неоднородной, если время выполнения каждого из блоков ПР Q1, Q2, …, Qs зависит от объемов обрабатываемых данных и/или их структуры, то есть разное для разных процессов.
Определение 2. Систему распределенных конкурирующих процессов будем называть однородной, если время выполнения Qj-го блока каждым из i-х процессов одинаково, то есть tij=tj,  ,
, 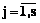 .
.
Определение 3. Систему конкурирующих процессов будем называть одинаково распределенной, если время tij выполнения каждого из блоков Qj, 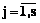 , ПР каждым из i-х процессов совпадает и равно ti для всех
, ПР каждым из i-х процессов совпадает и равно ti для всех  , то есть справедлива цепочка равенств ti1=ti2=…=tis=ti для всех
, то есть справедлива цепочка равенств ti1=ti2=…=tis=ti для всех  .
.
Время выполнения неоднородных распределенных процессов в асинхронном режиме при достаточном числе процессоров
Обозначим минимальное общее время выполнения n неоднородных распределенных конкурирующих процессов при ограниченном числе c копий ПР в МС с p процессорами в асинхронном режиме с учетом параметра e через  . Для его вычисления рассмотрим случаи неограниченного
. Для его вычисления рассмотрим случаи неограниченного  и ограниченного
и ограниченного  параллелизма.
параллелизма.

Пусть имеется система n=mc, m³2, 2£c£p, неоднородных распределенных конкурирующих процессов, причем число блоков s структурированного ПР не превосходит числа групп процессоров по с процессоров в каждой, то есть  . В этом случае без ограничения общности можно считать, что каждый Qj-й,
. В этом случае без ограничения общности можно считать, что каждый Qj-й, 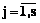 , блок i-го процесса, где i=lc+q,
, блок i-го процесса, где i=lc+q,  , l³0,
, l³0,  , закреплен за (q+c(r–1))-м процессором,
, закреплен за (q+c(r–1))-м процессором, 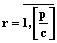 . Тогда для выполнения n процессов достаточно взять
. Тогда для выполнения n процессов достаточно взять  процессоров, а остальные
процессоров, а остальные 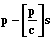 процессоров не будут задействованы.
процессоров не будут задействованы.
Пусть 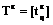 – n´s-матрица времени выполнения блоков ПР каждым из i-х процессов с учетом параметра e>0, где
– n´s-матрица времени выполнения блоков ПР каждым из i-х процессов с учетом параметра e>0, где 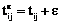 ,
,  ,
, 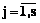 . Для вычисления минимального общего времени
. Для вычисления минимального общего времени  можно воспользоваться функционалом задачи Беллмана–Джонсона, который в данном случае будет иметь вид
можно воспользоваться функционалом задачи Беллмана–Джонсона, который в данном случае будет иметь вид
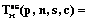

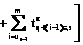 , (1)
, (1)
где  ,
,  ,
,  ,
, 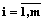 ,
, 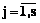 , а u1, u2, …, us–1 – целые числа.
, а u1, u2, …, us–1 – целые числа.
Пример 1. Рассмотрим интерпретацию формулы (1) на числовом примере. Пусть p=7, n=6, s=3, c=2, а время выполнения блоков процессами задано матрицей  .
.
Тогда m=3, следовательно, функционал (1) примет вид
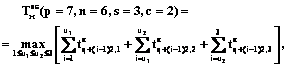
 .
.
1) При q=1 имеем:

Если u1=1, 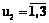 , если u1=2, u2=2,3, если u1=3, u2=3, тогда
, если u1=2, u2=2,3, если u1=3, u2=3, тогда
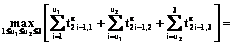



=max[12, 11, 10, 11, 10, 10]=12.
2) При q=2 имеем:

Если u1=1, 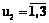 , если u1=2, u1=2,3, u1=3, u2=3, тогда
, если u1=2, u1=2,3, u1=3, u2=3, тогда


=max[8, 8, 10, 10, 12, 12]=12.
Следовательно, минимальное общее время выполнения n=6 неоднородных распределенных взаимодействующих конкурирующих процессов, использующих c=2 копии структурированного на s=3 блока ПР, в МС с p=7 процессорами в асинхронном режиме составит  . При этом будут использованы 6 процессоров.
. При этом будут использованы 6 процессоров.

 Рассмотрим алгоритм, позволяющий решить задачу определения минимального общего времени
Рассмотрим алгоритм, позволяющий решить задачу определения минимального общего времени  выполнения неоднородных распределенных конкурирующих процессов в асинхронном режиме значительно эффективнее.
выполнения неоднородных распределенных конкурирующих процессов в асинхронном режиме значительно эффективнее.
По заданным s, c,  и матрице
и матрице  ,
,  ,
, 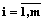 ,
, 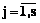 , строим c-слойный вершинно-взвешенный граф
, строим c-слойный вершинно-взвешенный граф  . Каждый q-й,
. Каждый q-й,  , слой графа
, слой графа  состоит из вершин
состоит из вершин  ,
, 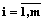 ,
, 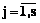 , которые расположены в узлах прямоугольной m´s-решетки, причем
, которые расположены в узлах прямоугольной m´s-решетки, причем  – входные вершины,
– входные вершины,  – выходные,
– выходные,  , t=(m–1)c (рис. 4). Дуги в каждом слое q отражают линейный порядок выполнения блоков Qj,
, t=(m–1)c (рис. 4). Дуги в каждом слое q отражают линейный порядок выполнения блоков Qj, 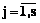 , ПР каждым (q+(i-1)c)-м процессом,
, ПР каждым (q+(i-1)c)-м процессом,  ,
, 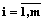 , а также линейный порядок использования каждого блока всеми m процессами. Таким образом, выведем следующую теорему.
, а также линейный порядок использования каждого блока всеми m процессами. Таким образом, выведем следующую теорему.
Теорема 1. Минимальное общее время выполнения n=mc, m³2, неоднородных распределенных конкурирующих процессов, использующих 2£c£p копий структурированного на  блока ПР с временем выполнения блоков с учетом дополнительных системных расходов
блока ПР с временем выполнения блоков с учетом дополнительных системных расходов  ,
,  ,
, 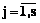 , в МС с p,
, в МС с p,  , процессорами в асинхронном режиме, определяется длиной критического пути в c-слойном вершинно-взвешенном графе
, процессорами в асинхронном режиме, определяется длиной критического пути в c-слойном вершинно-взвешенном графе  из начальной вершины
из начальной вершины  в конечную
в конечную  ,
,  ,
,  .
.
Пример 2. Используя данные примера 1, найти минимальное общее время  , используя алгоритм нахождения критического пути в c-слойном вершинно-взвешенном графе
, используя алгоритм нахождения критического пути в c-слойном вершинно-взвешенном графе  .
.
По заданным n=6, s=3 и матрице Te строим 2-слойный (c=2) вершинно-взвешенный граф  (рис. 5). Каждый слой содержит ms вершин, где m=n/c=3. Длина критического пути в графе равна 12, что совпадает с минимальным общим временем, полученным в примере 1.
(рис. 5). Каждый слой содержит ms вершин, где m=n/c=3. Длина критического пути в графе равна 12, что совпадает с минимальным общим временем, полученным в примере 1.
Асинхронный режим выполнения распределенных конкурирующих процессов в условиях ограниченного параллелизма
Рассмотрим случай ограниченного параллелизма, то есть когда число блоков структурированного ПР больше числа групп по c процессоров в каждой, то есть  ,
, 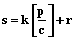 , k³1,
, k³1,  .
.
Как и в случае с одной копией ПР в общей памяти МС множество из s блоков разобьем на (k+1) групп по  блоков в каждой, за исключением (k+1)-й группы, которая будет содержать r блоков. Тогда матрицу
блоков в каждой, за исключением (k+1)-й группы, которая будет содержать r блоков. Тогда матрицу  ,
,  ,
,  , времени выполнения блоков разбиваем на (k+1) подматрицу
, времени выполнения блоков разбиваем на (k+1) подматрицу  ,
, 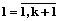 , размерностью
, размерностью  каждая, за исключением последней
каждая, за исключением последней  , которая будет содержать при s, не кратном
, которая будет содержать при s, не кратном  , только r столбцов, а остальные
, только r столбцов, а остальные  столбцов будут нулевыми. По каждой из подматриц
столбцов будут нулевыми. По каждой из подматриц  ,
, 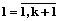 , строим (k+1)-ю линейную диаграмму Ганта, каждая из которых отображает во времени выполнение очередных
, строим (k+1)-ю линейную диаграмму Ганта, каждая из которых отображает во времени выполнение очередных  блоков структурированного ПР на
блоков структурированного ПР на  процессорах всеми n процессами, использующими ограниченное число c копий структурированного ПР. При r¹0 (k+1)-я диаграмма будет отражать выполнение последних r блоков на cr процессорах. На рисунке 6 представлена диаграмма Ганта для МС с параметрами p=7, n=4, s=3, c=2:
процессорах всеми n процессами, использующими ограниченное число c копий структурированного ПР. При r¹0 (k+1)-я диаграмма будет отражать выполнение последних r блоков на cr процессорах. На рисунке 6 представлена диаграмма Ганта для МС с параметрами p=7, n=4, s=3, c=2:
 .
.

 Cуммарное время выполнения всех процессов, использующих c копий ПР, в этом случае будет определяться как сумма длин критических путей в каждой из подряд идущих несовмещенных диаграмм Ганта. Однако это время можно сократить, если последовательно поблочно совмещать диаграммы Ганта, начиная со второй, по оси времени справа налево на максимально возможную величину, не нарушая технологические условия асинхронного режима. В результате совмещения получим результирующую совмещенную диаграмму Ганта (рис. 7).
Cуммарное время выполнения всех процессов, использующих c копий ПР, в этом случае будет определяться как сумма длин критических путей в каждой из подряд идущих несовмещенных диаграмм Ганта. Однако это время можно сократить, если последовательно поблочно совмещать диаграммы Ганта, начиная со второй, по оси времени справа налево на максимально возможную величину, не нарушая технологические условия асинхронного режима. В результате совмещения получим результирующую совмещенную диаграмму Ганта (рис. 7).
Полученная структура результирующей совмещенной диаграммы Ганта определяется матрицей T* (2), которая состоит из подматриц  . В матрице T* учтены как все горизонтальные, так и все вертикальные связи между блоками, а также связи между блоками из разных диаграмм Ганта. Отметим также, что результирующая матрица T* имеет размерность
. В матрице T* учтены как все горизонтальные, так и все вертикальные связи между блоками, а также связи между блоками из разных диаграмм Ганта. Отметим также, что результирующая матрица T* имеет размерность  , является блочной, симметричной, верхней диагональной относительно второй диагонали, типа Ганкелевой порядка k+1
, является блочной, симметричной, верхней диагональной относительно второй диагонали, типа Ганкелевой порядка k+1
 , (2)
, (2)
где  и
и  – матрицы вида
– матрицы вида
 ,
,  ,
,
 .
.
По матрице T* построим c-слойный вершинно-взвешенный граф 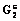 , аналогичный графу
, аналогичный графу  . Вершинам каждого слоя q размерности
. Вершинам каждого слоя q размерности  графа
графа 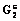 будут приписаны веса
будут приписаны веса  ,
,  ,
,  ,
, 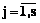 . Вершины
. Вершины  будут являться входными, а
будут являться входными, а  – выходными,
– выходными,  . Выведем следующую теорему.
. Выведем следующую теорему.
Теорема 2. Минимальное общее время  выполнения n, n³2, неоднородных распределенных конкурирующих процессов, использующих линейно структурированный на s, s³2, блоков ПР, с временем выполнения блоков с учетом дополнительных системных расходов e>0, задаваемых матрицей
выполнения n, n³2, неоднородных распределенных конкурирующих процессов, использующих линейно структурированный на s, s³2, блоков ПР, с временем выполнения блоков с учетом дополнительных системных расходов e>0, задаваемых матрицей  ,
,  ,
, 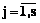 , в МС с p, p³2, процессорами и c³2 копиями структурированного ПР
, в МС с p, p³2, процессорами и c³2 копиями структурированного ПР  , в асинхронном режиме в случае неограниченного параллелизма
, в асинхронном режиме в случае неограниченного параллелизма  , определяется длиной критического пути из начальной вершины
, определяется длиной критического пути из начальной вершины  в конечную
в конечную  ,
,  , графа
, графа 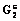 .
.
Пример 3. По значениям параметров диаграммы Ганта, изображенной на рис. 6, найти минимальное общее время  , используя алгоритм нахождения критического пути в c-слойном вершинно-взвешенном графе
, используя алгоритм нахождения критического пути в c-слойном вершинно-взвешенном графе 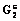 .
.
Так как 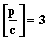 , то
, то 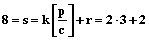 , следовательно, k=2, r=2. Матрицу Te разбиваем на подматрицы
, следовательно, k=2, r=2. Матрицу Te разбиваем на подматрицы  ,
,  , размерностью 4´3 каждая. Матрица T* будет иметь размерность
, размерностью 4´3 каждая. Матрица T* будет иметь размерность  и следующий вид:
и следующий вид:

Построим по матрице T* 2-слойный вершинно-взвешенный граф 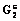 (рис. 8). Длина критического пути равна 22.
(рис. 8). Длина критического пути равна 22.
 Время выполнения однородных и одинаково распределенных конкурирующих процессов
Время выполнения однородных и одинаково распределенных конкурирующих процессов
Согласно определению 2, систему распределенных конкурирующих процессов будем считать однородной, если время выполнения каждого блока Qj, 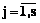 , каждым из процессов равное, то есть
, каждым из процессов равное, то есть 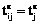 ,
,  ,
, 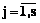 .
.
На рисунке 9 представлена диаграмма Ганта, иллюстрирующая выполнение однородных распределенных конкурирующих процессов при ограниченном числе копий ПР в МС с параметрами p=7, n=4, s=3, c=2,  .
.
Оценим общее время выполнения n однородных распределенных конкурирующих процессов в асинхронном режиме, использующих c копий структурированного ПР. Пусть – длительности выполнения каждого из блоков Qj, 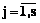 , ПР с учетом накладных расходов e,
, ПР с учетом накладных расходов e,  ,
, 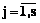 . Обозначим длительность выполнения всего ПР каждым из процессов через
. Обозначим длительность выполнения всего ПР каждым из процессов через  .
.
Покажем, что в этих условиях вычисление общего времени  в случае неограниченного параллелизма сводится к нахождению общего времени выполнения однородных распределенных процессов при одной копии структурированного ПР. При n=mc, m³2, 2£c£p, выполнение c копий структурированного ПР в асинхронном режиме равносильно выполнению c групп по m процессов, конкурирующих за использование одной копии ПР на
в случае неограниченного параллелизма сводится к нахождению общего времени выполнения однородных распределенных процессов при одной копии структурированного ПР. При n=mc, m³2, 2£c£p, выполнение c копий структурированного ПР в асинхронном режиме равносильно выполнению c групп по m процессов, конкурирующих за использование одной копии ПР на  процессорах.
процессорах.
Из формулы вычисления общего времени выполнения n однородных конкурирующих процессов, использующих одну копию структурированного ПР с учетом того, что n=mc, m³2, 2£c£p, получаем
 (3)
(3)
Для доказательства формулы (3) воспользуемся функционалом (1) задачи Беллмана–Джонсона, который для систем однородных конкурирующих процессов примет вид
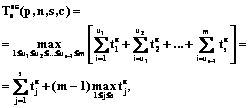
где  ,
,  ,
, 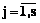 , а u1, u2, …, us–1 – целые числа.
, а u1, u2, …, us–1 – целые числа.

 В случае, когда
В случае, когда  ,
,  , k>1, матрица времени выполнения блоков ПР строится аналогично матрице T*. Отличие в том, что в каждой из подматриц
, k>1, матрица времени выполнения блоков ПР строится аналогично матрице T*. Отличие в том, что в каждой из подматриц  ,
,  , матрицы T* все строки совпадают. Тогда, по аналогии с теоремой 2, общее время
, матрицы T* все строки совпадают. Тогда, по аналогии с теоремой 2, общее время  выполнения n распределенных однородных конкурирующих процессов при ограниченном числе копий ПР определяется длиной критического пути из начальной вершины в конечную соответствующего сетевого графа.
выполнения n распределенных однородных конкурирующих процессов при ограниченном числе копий ПР определяется длиной критического пути из начальной вершины в конечную соответствующего сетевого графа.
Если  ,
, 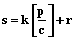 , k³1,
, k³1,  , то последняя подматрица
, то последняя подматрица  матрицы T* будет содержать
матрицы T* будет содержать  нулевых столбцов.
нулевых столбцов.
Определение 4. Однородное структурирование ПР на s блоков с временем выполнения , 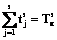 , будем называть равномерным, если
, будем называть равномерным, если 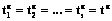 .
.
Следствие. В случае равномерного структурирования для вычисления минимального общего времени выполнения распределенных конкурирующих процессов при ограниченном числе копий программного продукта имеют место формулы
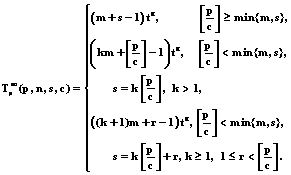
Рассмотрим систему одинаково распределенных конкурирующих процессов. Время выполнения всех ее блоков с учетом накладных расходов e каждым из i-х процессов совпадает и равно 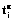 , то есть справедлива цепочка равенств
, то есть справедлива цепочка равенств  для всех
для всех  .
.
На рисунке 10 представлена диаграмма Ганта, иллюстрирующая выполнение одинаково распределенных конкурирующих процессов в МС с параметрами p=7, n=4, s=3, c=2,  в случае неограниченного
в случае неограниченного  параллелизма.
параллелизма.
Обозначим через  суммарное время выполнения каждого из блоков Qj,
суммарное время выполнения каждого из блоков Qj, 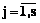 , всеми m процессами из q-й группы, а
, всеми m процессами из q-й группы, а  – максимальное время выполнения блока из этой группы,
– максимальное время выполнения блока из этой группы,  . Справедлива следующая теорема.
. Справедлива следующая теорема.
Теорема 3. Минимальное общее время вы- полнения n, n³2, одинаково распределенных конкурирующих процессов, использующих структурированный на s, s³2, блоков ПР в МС с p, p³2, процессорами в асинхронном режиме при ограниченном числе копий ПР составляет величину  , равную
, равную

Для доказательства рассмотрим сначала случай, когда 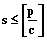 или
или  , но
, но  . Воспользуемся функционалом (1) задачи Беллмана–Джонсона, который для систем одинаково распределенных конкурирующих процессов примет вид
. Воспользуемся функционалом (1) задачи Беллмана–Джонсона, который для систем одинаково распределенных конкурирующих процессов примет вид 
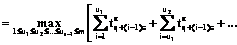

где  ,
,  ,
,  ,
, 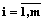 , u1, u2, …, us–1 – целые числа.
, u1, u2, …, us–1 – целые числа.
Рассмотрим далее случай, когда  , k>1, и
, k>1, и  . Вычисление общего времени
. Вычисление общего времени  с помощью функционала задачи Беллмана–Джонсона приводит к формуле
с помощью функционала задачи Беллмана–Джонсона приводит к формуле 

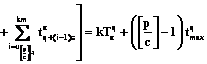 .
.
Здесь  ,
,  ,
, 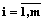 .
.
В случае, когда 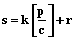 , k³1,
, k³1,  и
и 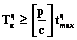 , вычисление общего времени с помощью функционала задачи Беллмана–Джонсона приводит к третьей формуле для вычисления
, вычисление общего времени с помощью функционала задачи Беллмана–Джонсона приводит к третьей формуле для вычисления
общего времени выполнения одинаково распределенных конкурирующих процессов при ограниченном числе копий ПР.
В заключение отметим, что рассмотренное обобщение математической модели с одним структурированным ПР (конвейером) на случай ограниченного числа ПР позволяет установить взаимосвязи мультиконвейерной обработки с аналогичной обработкой при одном программном конвейере, получить аналитические оценки общего времени выполнения конкурирующих процессов при ограниченном параллелизме и провести математическое исследование эффективности и оптимальности мультиконвейерной организации конкурирующих процессов, вскрыть потенциальные возможности роста ускорения вычислений, выполнить сравнительный анализ различных режимов такой обработки.
Литература
1. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. СПб: БХВ–Петербург, 2002.
2. Топорков В.В. Модели распределенных вычислений. М.: Физматлит, 2004.
3. Иванников В.П., Коваленко Н.С., Метельский В.М. О минимальном времени реализации распределенных конкурирующих процессов в синхронных режимах // Программирование. 2000. № 5. С. 44–52.
4. Павлов П.А. Оптимальность структурирования программных ресурсов при конвейерной распределенной обработке // Программные продукты и системы. 2010. № 3. С. 76–82.
5. Kapitonova Yu.V., Kovalenko N.S., Pavlov P.А. Optimality of systems of identically distributed competing processes // Cybernetics and Systems Analysis. NY: Springer. 2006, pp. 793–799.



 ,
, 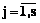 , времен выполнения блоков ПР распределенными взаимодействующими конкурирующими процессами; c копий (2£c£p) структурированного на блоки ПР, которые могут одновременно находиться в оперативной памяти, доступной для всех p процессоров, причем
, времен выполнения блоков ПР распределенными взаимодействующими конкурирующими процессами; c копий (2£c£p) структурированного на блоки ПР, которые могут одновременно находиться в оперативной памяти, доступной для всех p процессоров, причем  ; параметр e (e>0), характеризующий время дополнительных системных расходов, связанных с организацией конвейерного режима использования блоков структурированного ПР множеством взаимодействующих конкурирующих процессов при распределенной обработке.
; параметр e (e>0), характеризующий время дополнительных системных расходов, связанных с организацией конвейерного режима использования блоков структурированного ПР множеством взаимодействующих конкурирующих процессов при распределенной обработке. , l³0,
, l³0, 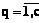 , осуществляется циклически по правилу: блок с номером
, осуществляется циклически по правилу: блок с номером  ,
, 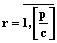 , распределяется на процессор с номером q+c(r–1).
, распределяется на процессор с номером q+c(r–1). , определяется наличием c процессоров и готовностью этой группы блоков к выполнению (программный блок считается готовым к выполнению, если он не выполняется ни на одном из процессоров);
, определяется наличием c процессоров и готовностью этой группы блоков к выполнению (программный блок считается готовым к выполнению, если он не выполняется ни на одном из процессоров); ,
,  .
.
 . Для его вычисления рассмотрим случаи неограниченного
. Для его вычисления рассмотрим случаи неограниченного  и ограниченного
и ограниченного  параллелизма.
параллелизма.
 . В этом случае без ограничения общности можно считать, что каждый Qj-й,
. В этом случае без ограничения общности можно считать, что каждый Qj-й,  , l³0,
, l³0,  , закреплен за (q+c(r–1))-м процессором,
, закреплен за (q+c(r–1))-м процессором,  процессоров, а остальные
процессоров, а остальные 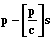 процессоров не будут задействованы.
процессоров не будут задействованы.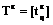 – n´s-матрица времени выполнения блоков ПР каждым из i-х процессов с учетом параметра e>0, где
– n´s-матрица времени выполнения блоков ПР каждым из i-х процессов с учетом параметра e>0, где 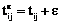 ,
, 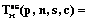

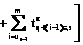 , (1)
, (1) ,
,  ,
,  ,
, 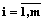 ,
,  .
.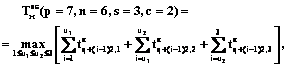
 .
.
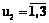 , если u1=2, u2=2,3, если u1=3, u2=3, тогда
, если u1=2, u2=2,3, если u1=3, u2=3, тогда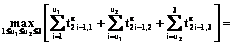






 . При этом будут использованы 6 процессоров.
. При этом будут использованы 6 процессоров.

 ,
,  . Каждый q-й,
. Каждый q-й,  ,
,  – входные вершины,
– входные вершины,  – выходные,
– выходные,  ,
,  ,
,  ,
, 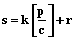 , k³1,
, k³1,  .
. блоков в каждой, за исключением (k+1)-й группы, которая будет содержать r блоков. Тогда матрицу
блоков в каждой, за исключением (k+1)-й группы, которая будет содержать r блоков. Тогда матрицу  ,
,  , времени выполнения блоков разбиваем на (k+1) подматрицу
, времени выполнения блоков разбиваем на (k+1) подматрицу  ,
, 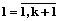 , размерностью
, размерностью  каждая, за исключением последней
каждая, за исключением последней  , которая будет содержать при s, не кратном
, которая будет содержать при s, не кратном  столбцов будут нулевыми. По каждой из подматриц
столбцов будут нулевыми. По каждой из подматриц  процессорах всеми n процессами, использующими ограниченное число c копий структурированного ПР. При r¹0 (k+1)-я диаграмма будет отражать выполнение последних r блоков на cr процессорах. На рисунке 6 представлена диаграмма Ганта для МС с параметрами p=7, n=4, s=3, c=2:
процессорах всеми n процессами, использующими ограниченное число c копий структурированного ПР. При r¹0 (k+1)-я диаграмма будет отражать выполнение последних r блоков на cr процессорах. На рисунке 6 представлена диаграмма Ганта для МС с параметрами p=7, n=4, s=3, c=2: .
.

 . В матрице T* учтены как все горизонтальные, так и все вертикальные связи между блоками, а также связи между блоками из разных диаграмм Ганта. Отметим также, что результирующая матрица T* имеет размерность
. В матрице T* учтены как все горизонтальные, так и все вертикальные связи между блоками, а также связи между блоками из разных диаграмм Ганта. Отметим также, что результирующая матрица T* имеет размерность  , является блочной, симметричной, верхней диагональной относительно второй диагонали, типа Ганкелевой порядка k+1
, является блочной, симметричной, верхней диагональной относительно второй диагонали, типа Ганкелевой порядка k+1 , (2)
, (2) ,
,  ,
, .
.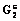 , аналогичный графу
, аналогичный графу  графа
графа  ,
,  – выходными,
– выходными,  , в асинхронном режиме в случае неограниченного параллелизма
, в асинхронном режиме в случае неограниченного параллелизма 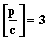 , то
, то 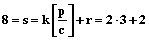 , следовательно, k=2, r=2. Матрицу Te разбиваем на подматрицы
, следовательно, k=2, r=2. Матрицу Te разбиваем на подматрицы  , размерностью 4´3 каждая. Матрица T* будет иметь размерность
, размерностью 4´3 каждая. Матрица T* будет иметь размерность  и следующий вид:
и следующий вид:

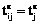 ,
,  .
. ,
,  .
. в случае неограниченного параллелизма сводится к нахождению общего времени выполнения однородных распределенных процессов при одной копии структурированного ПР. При n=mc, m³2, 2£c£p, выполнение c копий структурированного ПР в асинхронном режиме равносильно выполнению c групп по m процессов, конкурирующих за использование одной копии ПР на
в случае неограниченного параллелизма сводится к нахождению общего времени выполнения однородных распределенных процессов при одной копии структурированного ПР. При n=mc, m³2, 2£c£p, выполнение c копий структурированного ПР в асинхронном режиме равносильно выполнению c групп по m процессов, конкурирующих за использование одной копии ПР на  (3)
(3)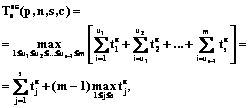


 , k>1, матрица времени выполнения блоков ПР строится аналогично матрице T*. Отличие в том, что в каждой из подматриц
, k>1, матрица времени выполнения блоков ПР строится аналогично матрице T*. Отличие в том, что в каждой из подматриц 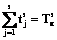 , будем называть равномерным, если
, будем называть равномерным, если 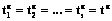 .
.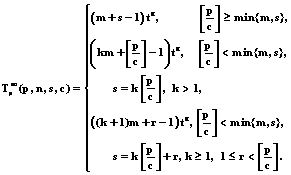
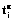 , то есть справедлива цепочка равенств
, то есть справедлива цепочка равенств  для всех
для всех  в случае неограниченного
в случае неограниченного  суммарное время выполнения каждого из блоков Qj,
суммарное время выполнения каждого из блоков Qj,  – максимальное время выполнения блока из этой группы,
– максимальное время выполнения блока из этой группы,  , равную
, равную
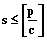 или
или  . Воспользуемся функционалом (1) задачи Беллмана–Джонсона, который для систем одинаково распределенных конкурирующих процессов примет вид
. Воспользуемся функционалом (1) задачи Беллмана–Джонсона, который для систем одинаково распределенных конкурирующих процессов примет вид 
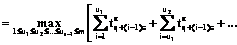

 ,
,  . Вычисление общего времени
. Вычисление общего времени 

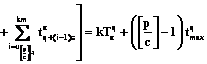 .
. ,
, 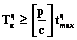 , вычисление общего времени с помощью функционала задачи Беллмана–Джонсона приводит к третьей формуле для вычисления
, вычисление общего времени с помощью функционала задачи Беллмана–Джонсона приводит к третьей формуле для вычисления