Для получения биологически активных веществ, белков, микроорганизмов и порохов зачастую нельзя применить тепловые способы обработки, поскольку под воздействием положительных температур могут изменяться структура вещества и его физико-химические свойства. Поэтому сегодня на химических, биотехнологических, фармацевтических производствах востребован процесс вакуумной сублимационной сушки (ВСС). Однако этот процесс имеет ряд недостатков, одним из которых является повышенное энергопотребление (по сравнению с другими способами сушки) [1].
Перед разработчиками стояла задача создать ПО, позволяющее смоделировать процесс ВСС и описать его в единичном объеме. Для ее решения была разработана модель, рассматривающая влияние температурных режимов на ход сублимации. Актуальность задачи обусловлена тем, что режим теплоподвода является важным фактором ведения процесса: повышение температуры позволяет интенсифицировать процесс и сократить время сушки, однако превышение критического значения может привести к расплавлению материала.
Описание модели
На рисунке 1 представлена схема процесса сублимационной сушки, на которой показан так называемый флакон с двухфазовой субстанцией – льдом и высушенным продуктом. Между слоями находится граница раздела двух фаз, смещающаяся в ходе сушки вниз. Теплота к материалу подводится двумя способами: тепловым излучением от верхней полки и кондуктивным теплоподводом от нижней.
При разработке математической модели были приняты следующие допущения:
1) все потоки тепла и массы в системе имеют одно измерение и направлены вдоль нормали к поверхностям;
2) сушка вымораживанием протекает под воздействием теплового излучения от полки сверху и кондуктивного теплоподвода от полки снизу;
3) во время сушки замороженный продукт условно можно разделить на две части: верхнюю – слой высушенного материала (R) и нижнюю – слой льда (С); граница между слоями в процессе сушки движется сверху вниз;
4) влагосодержание замороженного продукта принимается равным начальному, влагосодержание высушенного продукта – эквивалентному;
5) высушенные и замороженные участки рассматриваются как гомогенные с точки зрения постоянства теплопроводности, температурной диффузии, плотности и удельной теплоемкости, описываемых при помощи эквивалентных значений.
Расчет температурного профиля двух участков образца (высушенного и замороженного) идет одновременно и связан через подвижную границу раздела двух фаз. Проверкой его правильности являются температура на границе раздела фаз и поток тепла и влаги через нее.
Модель состоит из нестационарных балансовых энергетических уравнений и соответствующих граничных и начальных условий, записанных для областей замороженного слоя С и высушенного R [2].
Дифференциальные уравнения, начальные и граничные условия могут быть записаны в следующем виде.
1. Для слоя С (замороженный слой – лед).
 Уравнение теплопроводности для замороженного материала:
Уравнение теплопроводности для замороженного материала:
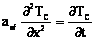 (1)
(1)
в диапазоне 0£x0; X(t) – подвижная граница; граничные условия на дне флакона:
TC=T0, где x=0, t>0. (2)
Уравнение изменения температуры пограничного слоя на границе с сухим слоем за счет испарения:
 , (3)
, (3)
где x=XC(t), t>0;
начальные условия: TC=TS, (4)
0£x
Здесь λ – теплопроводность; T0 – температура полки; TS – равновесная температура сублимации; TH – температура излучающей поверхности; TL – температура поверхности материала, нагреваемой излучением; L – толщина слоя материала; x – координата; используемые в модели индексы: ef – замороженный слой, ed – высушенный слой, eq – равновесный слой, i – исходный (замороженный) слой; TC – температура в слое замороженного материала; α – коэффициент температуропроводности; t – время; W – среднее влагосодержание по исходному материалу; ρbu – насыпная плотность высушенного материала; ∆HS – равновесная теплота сублимации; XС – положение границы между замороженным и высушенным слоями материала при наличии нагрева теплопроводностью.
2. Для слоя R (высушенный слой).
Уравнение теплопроводности для высушенного материала:
 (5)
(5)
в диапазоне XC(t)£x£L, t>0;
граничные условия: TR=TL, (6)
x=L, t>0.
Уравнение изменения температуры пограничного слоя сухого материала на границе с замороженным слоем:
 ; (7)
; (7)
x=XC, t>0;
начальные условия:
TR=TS, 0£x£L, t=0. (8)
 Здесь TR – температура в слое высушенного материала; XR – положение границы между замороженным и высушенным слоями материала при наличии нагрева излучением.
Здесь TR – температура в слое высушенного материала; XR – положение границы между замороженным и высушенным слоями материала при наличии нагрева излучением.
На границе раздела фаз должны выполняться равенства температур ТR=ТC, а также потоков тепла и массы.
Для нахождения температурного профиля воспользуемся разностной схемой Кранка–Николсона. Она является абсолютно устойчивой, поэтому шаг по времени может быть выбран достаточно большой для ускорения расчета, но это может привести к потере участка высушенного материала за период Δt. Чтобы избежать неточности, необходимо учитывать скорость удаления влаги и в соответствии с этим вести перерасчет шага по времени, уменьшая или увеличивая его в процессе расчета [3].
Изменение координаты границы замороженного слоя за счет подвода тепла от нижней полки описывается уравнением

 (9)
(9)

Уравнение для изменения влагосодержания в материале:
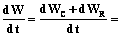
 (10)
(10)
Алгоритм расчета
Для решения уравнений (1)–(10) был разработан алгоритм, графически представленный на рисунке 2. Он позволяет рассчитать температурные профили и изменение влагосодержания в материале. Порядок действий алгоритма следующий.
1. Задаются начальные и граничные условия.
2. Оценивается величина шага в замороженном (С) и высушенном (R) слоях.
3. Одновременно рассчитываются температурные профили в замороженном (С) и высушенном (R) слоях.
4. Сравниваются конечные значения температуры на границе раздела фаз, и при необходимости уточняется шаг по времени и координате.
5. Полученное значение фактической температуры сравнивается с критической температурой.
6. Рассчитывается изменение влагосодержания образца и нового положения границы раздела фаз.
7. Фактическое значение влажности сравнивается с требуемым значением остаточного влагосодержания.
8. Делается вывод о завершении процесса сушки.
ПО и результаты расчета
Для описания процесса ВСС разработано ПО на С++ с применением блочного подхода. В состав ПО входят блок ввода начальных условий и ограничений, блок математического моделирования и блок отображения результатов.
Разработанная программа позволяет рассчитать все возможные температурные режимы проведения процесса, варьировать массу загрузки. На основании полученных данных могут быть выбраны параметры проведения процесса.
 Результат работы ПО – графические зависимости температурного профиля по высоте флакона, а также кинетика вакуумной сублимационной сушки (рис. 3). Программа рассчитывает три стадии ВСС: сублимационную сушку в изотермичных условиях, неизотермичную сушку и тепловую изотермичную сушку.
Результат работы ПО – графические зависимости температурного профиля по высоте флакона, а также кинетика вакуумной сублимационной сушки (рис. 3). Программа рассчитывает три стадии ВСС: сублимационную сушку в изотермичных условиях, неизотермичную сушку и тепловую изотермичную сушку.
Графики сублимационной сушки показывают характер изменения температуры в процессе ВСС. На первой (рис. 3а) и третьей (рис. 3в) стадиях сушки температура не меняется, следовательно, во всем объеме флакона она остается неизменной.
На второй стадии (рис. 3б) температура все время меняется, что отображается на графической зависимости. На рисунках 3г, 3д, 3е соответственно показаны расчетные значения изменения влагосодержания во времени для каждой из трех стадий. В ходе моделирования пользователь может одновременно рассматривать результаты нескольких экспериментов, варьируя характер температурного режима.
В заключение отметим, что разработанное ПО позволяет вскрыть процессы, протекающие в единичном объеме в ходе ВСС. Варьируя температуру процесса, пользователь наблюдает за откликом, определяя благоприятные для ВСС условия. Исследуя различные режимы процесса, можно повысить эффективность, а также снизить время сублимационной сушки.
Литература
1. Семенов Г.В. Вакуумная сублимационная сушка. Основные понятия и определения // Сублимационная сушка в фармацевтической и пищевой промышленности: матер. Междунар. науч.-технич. конф. М.: МГУПБ, 2005. С. 92–98.
2. Nastaj J.F. Some aspects of freeze drying of dairy biomaterials // Drying technology. 1996. № 14 (9), pp. 1967–2002.
3. Кольцова Э.М., Гордеев Л.С. Методы синергетики в химии и химической технологии. М.: Химия, 1999. 256 с.



 Уравнение теплопроводности для замороженного материала:
Уравнение теплопроводности для замороженного материала: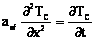 (1)
(1) , (3)
, (3) (5)
(5) ; (7)
; (7)

 (9)
(9)
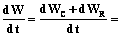
 (10)
(10)
