Литейное производство цветных металлов в отличие от литья черных металлов является малотоннажным. Однако ассортимент продукции, производимой из цветных металлов, намного шире. При смене ассортимента продукции технолог вынужден изменять технологические режимы литья. Процесс подбора нужного режима достаточно сложный и при традиционном подходе требует постановки специальных физических экспериментов, а также большого количества времени, иногда измеряемого месяцами. Существенно сократить материальные затраты и потери времени можно за счет замены физического эксперимента вычислительным, который проводится не на реальном технологическом процессе, а на его виртуальном физико-математическом аналоге. Поэтому задача использования компьютерного моделирования для управления технологическим процессом и повышения его эффективности, направленная на улучшение качества продукции и увеличение производительности оборудования, безусловно, является актуальной.
Программа выбора технологических режимов литья состоит из модулей гидродинамики, теплообмена, оптимизации и визуализации. Первые два модуля описаны в [1]. В данной работе приведем описание модуля оптимизации.
Задача оптимизации ставилась следующим образом: необходимо получить непрерывно-литой слиток, температурное поле которого в процессе получения удовлетворяет заданным критериям при заданных ограничениях на технологические параметры литья.
Математическая постановка задачи сформулирована как минимизация функционала
F=Ij®min, j=1, …, 6 (1)
при заданных краевых условиях
ji(X)=0, i=1, …, m1 (2)
и ограничениях
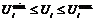 ; i=1, …, n, (3)
; i=1, …, n, (3)
Yi(U)=0, i=1, …, m2, (4)
Si(U)£0, i=1, …, m3, (5)
где X – вектор фазовых координат, компоненты которого измеряются (контролируются), но не регулируются; U – вектор параметров управления, компоненты которого контролируются и регулируются; n – количество оптимизируемых параметров (координат вектора управления);  и
и 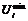 – максимальное и минимальное значения i-го оптимизируемого параметра Ui; m1 – количество ограничений типа (2); m2 – количество ограничений типа (4); m3 – количество ограничений типа (5).
– максимальное и минимальное значения i-го оптимизируемого параметра Ui; m1 – количество ограничений типа (2); m2 – количество ограничений типа (4); m3 – количество ограничений типа (5).
Для решения задачи (1)–(5) использовался метод случайного поиска с самообучением и адаптацией на рабочих и пробных шагах [2]. К несомненным преимуществам данного метода оптимизации по сравнению с градиентными методами следует отнести существенно меньшие затраты машинного времени при большом числе оптимизируемых параметров, простоту учета функциональных ограничений и краевых условий, высокую помехозащищенность.
В связи с тем, что понятие «качество слитка» является весьма емким и содержит большое число показателей, ни один из которых не может быть измерен непосредственно в процессе работы, в [3] предложено управлять качеством процесса по косвенным показателям. В качестве критериев оптимальности были использованы критерии, приведенные в таблице 1 и являющиеся функциями температурного поля.
В качестве оптимизируемых технологических параметров литья были взяты следующие: U1 – скорость литья; U2 – температура расплава; U3 – температура охлаждающей воды; U4 – длина кристаллизатора; U5 – время останова для дискретно-непрерывного литья.
Далее в качестве примера приводятся некоторые результаты оптимизации для медного слитка и слитка из сплава Al (40 %)+Cu (60 %) при литье вниз. Значения технологических параметров следующие: длина кристаллизатора (Lкр) – 0,8 м; радиус слитка (R) – 0,1 м; скорость литья (uлит) – 0,04 м/с; количество оптимизируемых параметров (n) – 5. Расчет критериев осуществлялся при исходных данных, представленных в таблице 2.
Граничные значения оптимизируемых параметров взяты из результатов предварительных расчетов таким образом, чтобы глубина зоны затвердевания не превышала высоту кристаллизатора.
Таблица 1
Критерии оптимальности
|
Критерий
|
Описание
|
|
 →min →min
|
Минимизация градиентов температур по толщине затвердевшей корки
|
|
 →min →min
|
Равномерность теплоотвода внутри затвердевшей корки
|
|
 →min →min
|
Линейность распределения температуры в продольном сечении затвердевающей части слитка
|
|
 →min →min
|
Равенство скорости охлаждения поверхности слитка в каждый момент времени скорости охлаждения в момент окончания затвердевания (приближение к режиму охлаждения без термических напряжений)
|
|
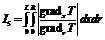 →min →min
|
Скорость продвижения фронта затвердевания, определяющая направление и характер роста кристаллов
|
Таблица 2
Оптимизируемые параметры
|
Параметр
|
Значение параметра
|
Приращение, DU 0
|
|
Начальное, U0
|
Нижнее, Uмин
|
Верхнее, Uмакс
|
|
U1
|
-0,04
|
-0,05
|
-0,001
|
0,003
|
|
U2
|
1430 (Cu)
1000 (Al+Cu)
|
1390 (Cu)
980 (Al+Cu)
|
1450 (Cu)
1200(Al+Cu)
|
4
|
|
U3
|
295
|
280
|
310
|
2
|
|
U4
|
0,8
|
0,3
|
1
|
0,047
|
|
U5
|
0
|
1
|
30
|
1,933
|
В результате расчета для литья вниз получены наборы оптимальных значений технологических параметров, соответствующие критериям (I1–I5) и представленные в таблице 3.
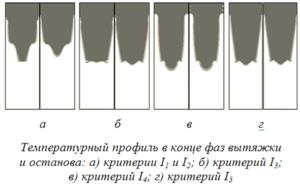
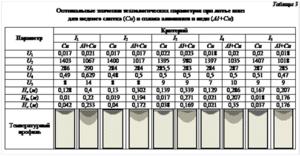 Температурный профиль включает три зоны: жидкий расплав, двухфазная зона и затвердевший металл. В градациях серого цвета эти зоны обозначены соответственно темным, промежуточным и светлым тонами. Зона кристаллизации (двухфазная зона) имеет характерный для литья вниз вид фигуры «перевернутый колокол». Условия затвердевания оценивались тремя параметрами температурного профиля: Hз – глубина зоны затвердевания, определяется как максимальное расстояние от верхнего края кристаллизатора до границы затвердевшего металла; Hдз – ширина двухфазной зоны, определяется максимальным расстоянием между границами жидкого и затвердевшего металла; Hс – высота контакта жидкого металла со стенками кристаллизатора. Форма и глубина зоны затвердевания, а также ширина двухфазной зоны являются важными показателями процесса формирования непрерывно-литого слитка. Они определяют характер и степень зональной ликвации и дендритной пористости в слитке, а также прочность и пластичность литого металла.
Температурный профиль включает три зоны: жидкий расплав, двухфазная зона и затвердевший металл. В градациях серого цвета эти зоны обозначены соответственно темным, промежуточным и светлым тонами. Зона кристаллизации (двухфазная зона) имеет характерный для литья вниз вид фигуры «перевернутый колокол». Условия затвердевания оценивались тремя параметрами температурного профиля: Hз – глубина зоны затвердевания, определяется как максимальное расстояние от верхнего края кристаллизатора до границы затвердевшего металла; Hдз – ширина двухфазной зоны, определяется максимальным расстоянием между границами жидкого и затвердевшего металла; Hс – высота контакта жидкого металла со стенками кристаллизатора. Форма и глубина зоны затвердевания, а также ширина двухфазной зоны являются важными показателями процесса формирования непрерывно-литого слитка. Они определяют характер и степень зональной ликвации и дендритной пористости в слитке, а также прочность и пластичность литого металла.
На основании анализа результатов, представленных в таблице 3, можно сделать следующие выводы.
 1. Наибольшее влияние на значения всех критериев оказывают скорость литья U1, время останова U5 и длина кристаллизатора U4, в то время как влияние температуры расплава U2 и температуры охлаждающей воды U3 значительно меньше. Так, для всех критериев оптимизации различие в значениях температуры расплава как для литья вниз, так и для литья вверх не превышает 17 K, а температуры воды 12 K, тогда как значения других параметров отличаются более чем на 50 %.
1. Наибольшее влияние на значения всех критериев оказывают скорость литья U1, время останова U5 и длина кристаллизатора U4, в то время как влияние температуры расплава U2 и температуры охлаждающей воды U3 значительно меньше. Так, для всех критериев оптимизации различие в значениях температуры расплава как для литья вниз, так и для литья вверх не превышает 17 K, а температуры воды 12 K, тогда как значения других параметров отличаются более чем на 50 %.
2. Наибольшую производительность при литье вниз обеспечивает критерий I3, причем скорость литья не превышает 0,023 м/с.
3. Максимальная температура заливаемого расплава, максимальная глубина зоны затвердевания и наибольшая длина кристаллизатора характерны для критерия I5 (для Сu) и критерия I1 (для Al+Cu).
4. В общем случае не требуется большого перегрева металла – Трасп не превышает 1406 K для Сu и 1072 K для Al+Cu.
5. Максимальная глубина зоны затвердевания для сплава Al+Cu и Cu наблюдается в случае использования критерия I1.
Кроме скорости литья, важным технологическим параметром, влияющим на производительность процесса и качество продукции, является время остановов при дискретно-непрерывном литье. Были произведены расчеты по оптимизации времени останова tост (U5) для критического режима литья вниз медной заготовки со скоростью 0,07 м/с. В этом режиме нарушалась сплошность зоны затвердевания.
Время останова ограничивалось интервалом: 1≤tост≤30 сек. Результаты расчетов оптимального времени останова по критериям следующие: для I1 – 11,6; для I2 – 11,6; для I3 – 6,5; для I4 – 10,1; для I5 – 16,95 (см. рис.).
Как видно из рисунка, температурные профили, рассчитанные в соответствии с критериями оптимальности, сохраняют сплошность, процесс затвердевания завершается в зоне кристаллизатора, следовательно, не происходит нарушение устойчивости. Максимальное время останова соответствует критерию I5, минимальное – критерию I3. Для критериев I1 и I2 оптимальное время останова одинаково. Зона затвердевания теряет вид фигуры «перевернутый колокол».
Таким образом, компьютерное моделирование позволяет технологу не только визуализировать процесс литья и рассчитывать его характеристики, но и управлять им исходя из заданных критериев оптимальности.
Литература
1. Жиганов Н.К., Фомина Е.Е. Программа моделирования процессов непрерывного литья цветных металлов и их сплавов // Программные продукты и системы. 2008. № 1. С. 10–12.
2. Жиглявский А.А., Жилинская А.Г. Методы поиска глобального экстремума. М.: Наука, 1991.
3. Беленький А.А. Математическое моделирование и оптимизация процесса литья и прокатки цветных металлов. М.: Металлургия, 1983. 160 с.

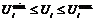 ; i=1, …, n, (3)
; i=1, …, n, (3) и
и 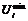 – максимальное и минимальное значения i-го оптимизируемого параметра Ui; m1 – количество ограничений типа (2); m2 – количество ограничений типа (4); m3 – количество ограничений типа (5).
– максимальное и минимальное значения i-го оптимизируемого параметра Ui; m1 – количество ограничений типа (2); m2 – количество ограничений типа (4); m3 – количество ограничений типа (5). →min
→min →min
→min →min
→min →min
→min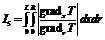 →min
→min
