Одной из важных составляющих численного моделирования в гидрогазодинамике является создание сетки, разбивающей расчетную область на отдельные ячейки. Развитие и широкое распространение коммерческих программных средств обусловили все возрастающую популярность неструктурированных сеток, построение которых, особенно для областей сложной формы, происходит гораздо быстрее благодаря большей гибкости и большей степени автоматизации. Однако изначально доминировавшие в вычислительной гидродинамике структурированные сетки до сих пор не потеряли своей актуальности, а в ряде случаев их применение оказывается предпочтительным.

Главной отличительной особенностью структурированных (регулярных) сеток является наличие явно выраженных сеточных (индексных) направлений, которые можно трактовать как криволинейную систему координат. Благодаря этому на регулярной сетке удается построить разностные схемы более высокого порядка точности, что особенно важно, например, для прямого численного моделирования турбулентных течений и решения задач аэроакустики.

При расчете течений в областях с подвижными границами регулярную сетку легко деформировать с помощью прямых интерполяционных формул, тогда как для неструктурированных сеток обычно вводится некая модель упругой деформации, требующая весьма затратного по времени итерационного решения вспомогательных уравне­ний. Регулярные сетки позволяют в большей степени векторизовать программу и использовать более эффективные численные методы (например, схемы с расщеплением по индексным направлениям). Работа со структурированной сеткой требует меньше вычислений, так как при равном количестве узлов (то есть при одинаковом пространственном разрешении) неструктурированная сетка имеет в 5–6 раз больше ячеек (тетраэдров) и в 3–4 раза больше граней. Наличие индексных координат обеспечивает прямой доступ к любой ячейке структурированной сетки и не требует хранения дополнительной информации о ее гранях, соседних ячейках и т.п.

В целом программы, использующие регулярные сетки, проще в реализации, менее требовательны к вычислительным ресурсам и в ряде случаев позволяют обеспечить более высокое качество численного моделирования в гидрогазодинамике. Поэтому для небольших научных групп (в частности, университетских), разрабатывающих собственные программы такого рода, вполне естественна ориентация на использование структурированных сеток.

В настоящей работе представлен комплекс программ для генерации двухмерных и трехмерных блочно-структурированных сеток, созданный при тесном сотрудничестве научных групп двух вузов – Санкт-Петербургского государственного политехнического университета (СПбГПУ) и Тверского государственного технического университета.

Начальная отработка базовых алгоритмов, реализованных в представляемом комплексе программ, была осуществлена при создании в 90-х годах интерактивного двухмерного генератора сеток MIG (Mesh Interactive Generator). Впоследствии, в 2000–2003 гг., усовершенствованная версия этого генератора была интегрирована в препроцессор гидродинамического пакета FLOS (Flow Studio, рис. 1), а также послужила основой для наполнения алгоритмической части трехмерного сеточного генератора ORIGGIN (Operative and Rati­onal Interactive Grid Generation Instrument, рис. 2). Отметим, что в настоящее время пакет FLOS широко используется в СПбГПУ, обеспечивая начальное освоение студентами методов инженерного анализа в гидродинамике с использованием современных программных средств, проведение циклов вычислительных лабораторных работ, выполнение исследовательских расчетов при подготовке отдельных выпускных бакалаврских работ и магистерских диссертаций. Генератор ORIGGIN входит в состав распределенной информационно-вычислительной системы, предназначенной для решения широкого круга задач вычислительной гидродинамики и теплообмена [1].

Построение многоблочной сетки в препроцессоре пакета FLOS происходит последовательно в три этапа: построение геометрической модели, расстановка граничных узлов, инициализация и при необходимости коррекция (улучшение) сетки. На каждом этапе на экране отображаются объекты соответствующего уровня и инструменты для работы с ними; имеется возможность масшта- бирования и оцифровки изображения, а также просмотра детальной информации об активном объекте.

На этапе геометрического моделирования создаются границы расчетной области, а также вспомогательные границы для разбиения области на блоки. Границы состоят из опорных точек, соединенных друг с другом прямолинейными отрезками, дугами окружности или NURB-сплайнами [2]. Сплайн задается набором базовых точек, через которые проходит кривая (для объектов сложной формы предусмотрена возможность чтения координат базовых точек из текстового файла); при необходимости пользователь может менять положение вспомогательных точек, влияющих на кривизну линии между базовыми точками. Для задания структуры сетки в каждом ее блоке назначаются вершины топологического прямоугольника (попутно определяется ориентация индексной системы координат в блоке) и указываются геометрические элементы, образующие границы блока. Если некоторые опорные точки нужно определить как узлы сетки (например, для реализации поставленных граничных условий), им можно присвоить статус узловых; естественно, вершины блоков всегда являются узловыми точками.

При расстановке узлов по границам блоков структурированной сетки, помимо соблюдения очевидного требования равенства числа узлов на противоположных сторонах блока, обычно следует обеспечить локальное сгущение узлов на некоторых участках границы (например, вблизи поверхности обтекаемого тела). В генераторе пакета FLOS для этого используется функция расстановки узлов на выделенном сегменте по закону геометрической прогрессии. При этом в качестве сегмента для расстановки узлов можно взять любой участок границы между ранее расставленными узлами (первоначально узлы располагаются в опорных точках границы), не содержащий внутри себя узловых опорных точек. В дополнение к стандартной функции расстановки узлов по сегменту реализованы авторские инструменты для модификации существующего распределения узлов, которые, как показала многолетняя практика применения пакета, значительно повышают удобство и эффективность работы с граничными узлами. Среди наиболее востребованных – функции изменения числа узлов на сегменте (с сохранением имеющейся неравномерности их распределения), перемещения выбранного узла вдоль границы (с пропорциональным смещением остальных узлов на сегменте) и притягивания узлов сегмента к выделенному узлу, а также функции прямого и инверсного переноса (копирования) распределения узлов с одного сегмента на другой. Для реализации перечисленных функций используется монотонный сплайн, аппроксимирующий текущее распределение узлов на выделенном сегменте границы, то есть зависимость относительной координаты узлов от их относительного номера. После построения сплайна не составит труда воспроизвести ту же неравномерность при расстановке нужного числа узлов на любом сегменте (в прямом или обратном порядке), перемещение узла по сегменту реализуется с помощью кусочно-ли­нейного распределения узлов вдоль индексной переменной (с изломом в выбранном узле), а притягивание узлов – простым нелинейным распре- делением (геометрической прогрессией по обе стороны от центра притяжения).

Для первичной расстановки внутренних узлов (инициализации) сетки в генераторе пакета FLOS используется метод линейной трансфинитной интерполяции [2]. Если качество получающейся при этом сетки не удовлетворяет пользователя, он имеет возможность ее корректировки внутри выделенного сегмента. Алгебраические методы корректировки сетки представлены двухмерными аналогами функций для работы с граничными узлами: изменение числа сеточных линий выбранного направления, перемещение выбранного узла или сеточной линии вдоль сеточных или координатных направлений (с линейно убывающим смещением остальных узлов на сегменте), притягивание узлов сегмента к выделенному узлу или сеточной линии (рис. 1). При необходимости можно инициализировать сетку внутри выделенного сегмента в соответствии с текущим распределением узлов на его границе по методу трансфинитной интерполяции. Имеется также возможность локального сглаживания сетки (устранения изломов сеточных линий) на основании решения уравнения Пуассона (метод Томпсона [2]) с управляющими функциями Томаса–Миддлкоффа [3]. При этом в процессе итерационного решения уравнения Пуассона целесообразно останавливаться после каждой итерации для визуальной оценки результата; как правило, желаемый эффект достигается уже после двух-трех итераций.

Как уже отмечалось, алгоритмы, отработанные в сеточном генераторе MIG (FLOS), использовались в процессе создания генератора двухмерных и трехмерных сеток ORIGGIN. При этом для алгоритмов, базирующихся на интерполяции вдоль кривой (расстановка узлов на ребрах, трансфинитная интерполяция и др.), обобщение на трехмерный случай фактически свелось к простому добавлению третьей координаты при вычислении длины дуги и в качестве интерполируемой величины. Среди дополнительных полезных опций, реализованных в генераторе, можно отметить функцию ортогонализации сетки вблизи выбранной границы, которая является модификацией описанной ранее функции смещения узлов со специально подобранным законом изменения величины смещения при удалении от границы. Естественно, ориентация на работу с трехмерными сетками потребовала более развитого графического интерфейса для визуализации и навигации по объектам.

Для построения трехмерных сеток в генераторе ORIGGIN предусмотрено несколько методов, простейшим из которых является выращивание трехмерной сетки из двухмерной (поверхностной) посредством поворота или линейного смещения. Также имеется возможность трансляции двухмерной сетки вдоль задаваемых направляющих, прямолинейных или криволинейных, с соответствующим линейным растяжением и поворотом начальной сетки или (в более общем случае) с плавным переходом от одной сетки к другой (например, от квадратной к круглой). Это позволяет быстро строить сетки, в частности, для расчета течения в трубах, диффузорах, переходниках и других каналах с плавно изменяющимся сечением.

В условиях более сложной геометрии для создания (инициализации) трехмерной сетки в ге- нераторе ORIGGIN применяется трансфинитная интерполяция, которая в общем случае требует задания сетки на всех шести ограничивающих поверхностях (гранях топологического куба). Сетки для плоских граней строятся как обычные двухмерные (с возможностью их пространственного смещения и поворота); для искривленных поверхностей используется метод проецирования плоской сетки [2]. С целью экономии затрат на построение поверхностных сеток предусмотрены неполные варианты трансфинитной интерполяции – по 4 граням и по 12 ребрам. При этом недостающие поверхностные сетки создаются автоматически с помощью трансфинитной интерполяции по двум индексным направлениям.

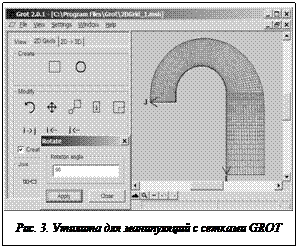
Полезным дополнением к описанным генераторам сеток может служить утилита GROT (Grid Operation Tool) для преобразования структурированных сеток без изменения расстановки узлов (рис. 3). Утилита позволяет, в частности, выполнить поворот, смещение и масштабирование сетки, отразить сетку относительно ее грани или координатной плоскости, изменить порядок и направление индексов, разрезать сетку на отдельные блоки или объединить пару блоков в единую сетку. Утилита работает как с двухмерными, так и с трехмерными сетками; также имеется возможность создания трехмерной сетки из двухмерной посредством поворота или линейного смещения с заданным коэффициентом неравномерности. Графический интерфейс позволяет визуально контролировать выполнение всех операций с возможностью масштабирования и оцифровки изображения.

На основании изложенного можно заключить, что представленный комплекс программ имеет простой и интуитивно понятный интерфейс, благодаря чему программы легко осваиваются начинающими пользователями и могут с успехом применяться в учебном процессе. В то же время функциональных возможностей комплекса вполне достаточно для построения высококачественных расчетных сеток при проведении научных исследований и решении практических задач в области гидродинамики и теплообмена.

Литература

1. Распределенная информационно-вычислительная система моделирования методами вычислительной гидродинамики / В.Д. Горячев [и др.] // Программные продукты и системы. 2004. № 3. С. 2–7.

2. Handbook of grid generation / J.F. Thompson, B.K. Soni, N.P. Weatherill (eds.). CRC Press, 1998, 1136 p.

3. Thomas P.D., Middlecoff J.D. Direct control of the grid point distribution in meshes generated by elliptic equations // AIAA Journal, 1980. Vol. 18. No. 6, pp. 652–656.