Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Полумарковские модели систем с нечеткими параметрами
Аннотация:Рассмотрены ограничения на существующие подходы к построению и использованию нечетких полумарковских моделей для анализа процессов функционирования систем. Выделены и описаны основные классы нечетких функций, которые целесообразно использовать в качестве нечетких отображений при построении полумарковских моделей систем с нечеткими параметрами. Представлен универсальный подход к анализу нечетких полумарковских моделей как с четкими, так и с нечеткими параметрами.
Abstract:The limitations of existing approaches to the construction and use of semi-fuzzy models for the analysis of the functioning of systems are considered. The main classes of fuzzy functions, which should be used as a fuzzy mappings in constructing models of semi-Markovian systems with fuzzy parameters, are allocated and described. An approach to the analysis of semi-fuzzy models, regardless of which of the options are clear, and which – fuzzy are presented.
| Авторы: Глушко С.И. (midli@mail.ru) - Смоленский филиал Национального исследовательского университета МЭИ, г. Смоленск, Россия, Бояринов Ю.Г. (byg@yandex.ru) - Филиал Московского энергетического института (технического университета) в г. Смоленске, кандидат технических наук | |
| Ключевые слова: нечеткое отображение, нечеткая функция, нечеткие параметры, нечеткая полумарковская модель |
|
| Keywords: fuzzy representation, fuzzy function, fuzzy parameters, fuzzy semi-Markov model |
|
| Количество просмотров: 9192 |
Версия для печати Выпуск в формате PDF (5.19Мб) Скачать обложку в формате PDF (1.31Мб) |
Сложность использования полумарковских моделей для анализа характеристик нахождения системы в различных состояниях обусловлена необходимостью учета множества неопределенных факторов, объективная информация о которых часто отсутствует либо является экспертной. Одним из подходов к решению этих проблем при анализе функционирования систем является использование нечетких полумарковских моделей, в которых для учета неопределенности факторов применяются различные способы введения нечеткости. Так, выражения для оценки распределения вероятностей состояний могут дополняться функциями принадлежности времени пребывания системы в соответствующих состояниях [1]. Недостаток данного способа в том, что нечеткими па- раметрами являются только время пребывания системы в различных состояниях, а также сложность задания соответствующих функций принадлежности. Другой способ заключается в том, что и вероятности состояний, и время пребывания системы в соответствующих состояниях заменяются на нечеткие числа (нечеткие множества), а обычные операции – на расширенные операции над нечеткими числами. При этом для определения результатов используются нечеткие отображения, реализуемые в соответствии с одним из известных подходов (нечеткие продукции, нечеткие отношения, нечеткие функции) [2–4]. К ограничениям этого способа относятся необходимость учета достаточно жестких требований к расширенным операциям, а также сложность согласования подходов к реализации различных нечетких отображений в рамках одной задачи. В данной работе выделены и рассмотрены основные классы нечетких функций, которые целесообразно использовать в качестве нечетких отображений при построении полумарковских моделей систем с нечеткими параметрами. Примером подобных систем может служить система технического обслуживания (ТО) и ремонта оборудования для трубопроводной транспортировки нефти. Опишем подход к анализу полумарковских моделей, не зависящий от того, какие из параметров являются четкими, а какие нечеткими. Пусть поведение системы задано совокупностью состояний S={S1, …, Sn} и множеством возможных переходов. Полумарковский процесс задается с помощью матрицы F(t)=||Fij(t)||n´n условных функций распределения продолжительности пребывания в состояниях, матрицы W=||wij||n´n переходных вероятностей вложенной марковской цепи и начального состояния процесса, из которого он стартует. Безусловные функции распределения Fi(t) определяются в соответствии с выражением Среднее время пребывания системы в соответствующих состояниях находится следующим образом: Асимптотическое поведение полумарковского процесса описывается финальным распределением вероятностей состояний вложенной марковской цепи и определяется в результате решения системы уравнений P=PW, P=(Р1, …, Рn) с учетом условия нормировки В стационарном режиме распределение вероятностей состояний для полумарковского процесса в целом определяется из выражения Параметры данного выражения могут быть и четкими, и нечеткими; произвольное отображение f : {P1, …, Pn, m1, …, mn}®pi (i=1, …, n) может представлять собой как четкую, так и нечеткую функцию. В соответствии с этим можно выделить следующие основные классы нечетких функций, которые целесообразно использовать в качестве нечетких отображений при построении полумарковских моделей систем с нечеткими параметрами: 1) четкие функции с распространением нечеткости от независимых переменных к зависимым; 2) нечеткие функции четких переменных; 3) нечеткие функции нечетких переменных. Рассмотрим использование этих отображений применительно к задаче построения и использования полумарковских моделей систем. Четкие функции с распространением нечеткости Пусть заданы вектор входных четких параметров A=(P1, …, Pn, m1, …, mn), вектор выходных четких параметров p=(p1, …, pn), четкая функция f: A®p, а также нечеткие множества Для простоты дальнейшего изложения заменим обозначения для вектора входных нечетких параметров на Тогда функция f распространяет нечеткость от входных переменных A, характеризующихся неопределенностью (заданных нечеткими множествами
где декартово произведение нечетких множеств Нечеткие функции четких и нечетких переменных Существуют различные способы представления нечетких функций, которые обусловливают применение соответствующих им методик расчета, например, с помощью – операций над нечеткими числами и переменными (аналогично типичному представлению четких функций); – композиции интервальных функций для всех α-уровней; – композиции интервалов нечетких значений нечеткой функции всех a-уровней. Рассмотрим особенности использования указанных способов. К ограничениям представления нечетких функций с использованием операций над нечеткими числами и переменными прежде всего стоит отнести необходимость учета достаточно жестких требований к этим операциям. При представлении нечеткой функции с помощью композиции интервальных функций для всех a-уровней (aÎ[0, 1]) каждое значение, принимаемое нечеткой функцией
где Отметим, что Таким образом, При представлении нечеткой функции с помощью композиции интервалов нечетких значений нечеткой функции для всех a-уровней
где Отметим, что
Нечеткие функции нечетких переменных могут быть построены и проанализированы аналогично нечетким функциям четких переменных. При анализе нечетких полумарковских моделей для вычисления нечетких функций на основе двух последних рассмотренных способов представления применима конструктивная методика, предложенная в работе. Данная методика позволяет вычислить границы интервалов результата Во-первых, задается значение ak-уровня из уровневого множества LA={a1, a2, …, ak, …, aK}, где 1=a1>a2>…>ak>…>aK=0. Во-вторых, для каждого ak покомпонентно задаются значения входных параметров:
то есть В-третьих, для каждого значения ak-уровня из уровневого множества с учетом покомпонентного задания значений входных параметров определяются границы интервалов нечеткого значения функции
Таким образом, при использовании данной методики не требуется учитывать ограничения, накладываемые операциями над нечеткими числами и переменными. При этом реализуется единый подход к совместному анализу как четких, так и нечетких параметров в полумарковской модели системы. Применение предложенной методики в АК «Транснефть» (г. Москва) позволило повысить эффективность системы технического обслуживания и ремонта оборудования для трубопроводной транспортировки нефти за счет рационализации сроков проведения ремонтных мероприятий и выбора видов ТО. Следует отметить, что методика допускает программную реализацию, которая может использоваться как компонент ПО информационных систем ТО и ремонта оборудования сложных технологических систем. Литература 1. Bhattacharyya M. Fuzzy Markovian decision process // Fuzzy Sets and Systems. 1998. Vol. 99, pp. 273–282. 2. Praba B., Sujatha R., Srikrishna S. Fuzzy reliability measures of fuzzy probabilistic semi-Markov model // Int. Journal of Recent Trend in Engineering. 2009. Vol. 2. No 2, pp. 25–29. 3. Praba B., Sujatha R., Srikrishna S. A study on homogeneous fuzzy semi-Markov model // Applied Mathematical Sciences. 2009. Vol. 3. No 50, pp. 2453–2467. 4. Метод построения нечеткой полумарковской модели функционирования сложной системы / Ю.Г. Бояринов [и др.] // Программные продукты и системы. 2010. № 3 (91). С. 26–31. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=3134&page=article |
Версия для печати Выпуск в формате PDF (5.19Мб) Скачать обложку в формате PDF (1.31Мб) |
| Статья опубликована в выпуске журнала № 2 за 2012 год. [ на стр. 146 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:







 и
и 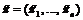 , определенные на множествах A и p соответственно.
, определенные на множествах A и p соответственно. , заданного на базовых множествах A=(A1, …, An).
, заданного на базовых множествах A=(A1, …, An). ), на выходные переменные p (путем формирования нечетких множеств
), на выходные переменные p (путем формирования нечетких множеств  ) в соответствии с принципом расширения при выполнении следующего соотношения:
) в соответствии с принципом расширения при выполнении следующего соотношения:

 является нечетким множеством, заданным на множестве A1´ …´An с функцией принадлежности
является нечетким множеством, заданным на множестве A1´ …´An с функцией принадлежности 

 , принадлежит интервалу, центр которого соответствует значению соответствующей четкой функции той же структуры, а радиус интервала равен длине левого (правого) растяжения данного нечеткого значения функции (при условии симметричности нечеткой функции). Поэтому при конкретном значении параметра a график нечеткой функции одной переменной представляет собой плоскую полосу (интервальную функцию), осью симметрии которой является график соответствующей четкой функции. Тогда нечеткая функция может быть представлена в виде композиции соответствующих интервальных функций для всех a-уровней:
, принадлежит интервалу, центр которого соответствует значению соответствующей четкой функции той же структуры, а радиус интервала равен длине левого (правого) растяжения данного нечеткого значения функции (при условии симметричности нечеткой функции). Поэтому при конкретном значении параметра a график нечеткой функции одной переменной представляет собой плоскую полосу (интервальную функцию), осью симметрии которой является график соответствующей четкой функции. Тогда нечеткая функция может быть представлена в виде композиции соответствующих интервальных функций для всех a-уровней:
 – интервальная функция;
– интервальная функция;  ,
, 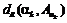 – левая и правая функции отклонения от функции при заданном значении ak; LA={a1, a2, …, ak, …, aK} – уровневое множество.
– левая и правая функции отклонения от функции при заданном значении ak; LA={a1, a2, …, ak, …, aK} – уровневое множество. и
и где
где 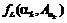 ,
,  – граничные функции при заданном значении a.
– граничные функции при заданном значении a.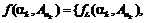


 – граничные функции, задающие левую и правую границы интервалов всех α-уровней нечетких значений нечеткой функции;
– граничные функции, задающие левую и правую границы интервалов всех α-уровней нечетких значений нечеткой функции;  – интервал a-уровня нечеткого значения функции для некоторой точки многомерного пространства входных нечетких параметров; LA – уровневое множество.
– интервал a-уровня нечеткого значения функции для некоторой точки многомерного пространства входных нечетких параметров; LA – уровневое множество.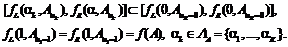
 и заключается в следующем.
и заключается в следующем.




 :
: