Все большее применение в промышленности и на транспорте находит контроль геометрических параметров деталей и узлов машиностроения с помощью лазерной триангуляции. Однако основными проблемами, препятствующими его внедрению, являются разнородность оцениваемых поверхностей и, как результат, неоптимальные условия работы сенсора, приводящие к возникновению шумов спеклов, что в конечном итоге увеличивает погрешность [1].
 Альтернативой указанному подходу может быть метод триангуляции с использованием зеркально отраженного излучения, так как чувствительность его больше [2]. На устройство для контроля параметров криволинейных поверхностей в 1994 г. выдан патент 2025659 (авторы: Андрейченко Ю.Я., Волошинов В.А., Волошинов Д.В., Самсонов В.В.). С помощью этого метода проще добиться приемлемого качества входного оптического сигнала. Кроме того, реализующая его оптическая схема более простая и дешевая, чем у интерферометра – устройства, реализующего еще один альтернативный оптический метод. Отметим, что рассматриваемый метод имеет значительное сходство с гартмановскими датчиками волнового фронта, имеющими большую чувствительность (до 0,001 длины волны света) и перспективными для различных применений.
Альтернативой указанному подходу может быть метод триангуляции с использованием зеркально отраженного излучения, так как чувствительность его больше [2]. На устройство для контроля параметров криволинейных поверхностей в 1994 г. выдан патент 2025659 (авторы: Андрейченко Ю.Я., Волошинов В.А., Волошинов Д.В., Самсонов В.В.). С помощью этого метода проще добиться приемлемого качества входного оптического сигнала. Кроме того, реализующая его оптическая схема более простая и дешевая, чем у интерферометра – устройства, реализующего еще один альтернативный оптический метод. Отметим, что рассматриваемый метод имеет значительное сходство с гартмановскими датчиками волнового фронта, имеющими большую чувствительность (до 0,001 длины волны света) и перспективными для различных применений.
В данной статье подробно описан и обоснован вывод расчетных формул и приведены алгоритмы получения профилей и контурных картин поверхностей вращения способом триангуляции с использованием зеркально отраженного излучения.
Рассматриваемые контролируемые изделия имеют вид тела вращения с криволинейной наружной поверхностью:
F(r, j, z)=0, (1)
где r, j, z – цилиндрические координаты.
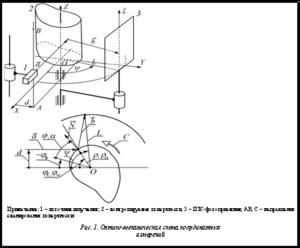
Рассмотрим модель оптического сканирования в приближении геометрической оптики при условии, что падающий и отраженный пучки света являются тонкими (см. [3]). При этом важно, что, во-первых, поперечная ширина тонкого пучка не учитывается в расчетах и, во-вторых, прохождение тонкого пучка в пространстве описывается положением его центрального луча.
На рисунке 1 изображена тестируемая поверхность в зоне оптического контроля. Параллельно оси OZ со смещением на величину d в положительном направлении оси OY проведена прямая AB. В направлении данной прямой производится сканирование поверхности вдоль оси вращения источником излучения. Луч  , падающий на поверхность, перпендикулярен плоскости YOZ и зеркально отражается относительно вектора нормали
, падающий на поверхность, перпендикулярен плоскости YOZ и зеркально отражается относительно вектора нормали  .
.
Отраженный луч  регистрируется матричным фотоприемником, расположенным так, чтобы столбцы матрицы были параллельны оси x. С этой осью совмещается серединный столбец матрицы. Для поиска луча
регистрируется матричным фотоприемником, расположенным так, чтобы столбцы матрицы были параллельны оси x. С этой осью совмещается серединный столбец матрицы. Для поиска луча  , отраженного от поверхностей с различными наклонами, перед началом измерений фотоприемник имеет возможность перемещаться по дуге радиуса L в диапазоне углов [y1, y2].
, отраженного от поверхностей с различными наклонами, перед началом измерений фотоприемник имеет возможность перемещаться по дуге радиуса L в диапазоне углов [y1, y2].
Информативными параметрами являются угол y, который отсчитывается от положительного направления оси OX и соответствует энергетическому центру отраженного пучка на матричном фотоприемнике, а также координата x этого энергетического центра на фотоприемнике.
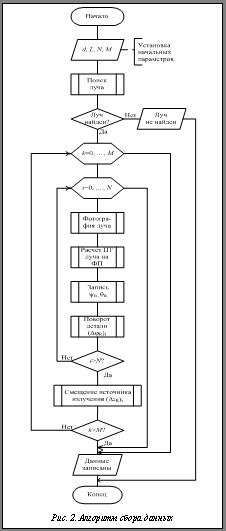 Сканирование всей поверхности осуществляется шаговым разворотом контролируемого объекта вокруг оси OZ и дискретным перемещением источника света по прямой AB в точках с координатами zk=zk-1+Dz. Алгоритм сбора данных приведен на рисунке 2.
Сканирование всей поверхности осуществляется шаговым разворотом контролируемого объекта вокруг оси OZ и дискретным перемещением источника света по прямой AB в точках с координатами zk=zk-1+Dz. Алгоритм сбора данных приведен на рисунке 2.
Формулы для определения координат освещенной точки контролируемой поверхности на каждом шаге сканирования получены из законов геометрической оптики:
 ,
,  . (2)
. (2)
Эти соотношения определяют принадлежность входящих в них векторов одной плоскости и равенство углов падения и отражения. Дополняя их уравнением падающего луча, получаем математическую модель оптической схемы в виде системы из четырех уравнений.
Для упрощения системы уравнений (2) переходим от декартовых координат {x, y, z} к системе цилиндрических координат {rc, jc, zc}. Располагаем ее так, чтобы направления осей z и zc совпадали, а отсчет углов jc начинался от положительного направления оси OX в сторону положительного направления оси OY.
Из исходной системы уравнений путем линейных преобразований авторами ранее были получены [4] два дифференциальных уравнения. Они связывают rc и его первую производную по какой-либо другой координате – jc или zc:
 ,
,
 , (3)
, (3)
где jR – угол поворота контролируемого объекта; zR – смещение источника излучения;  и
и  – функции четырех переменных. Переменные jR, zR задаются независимо известным способом. Их отсчет ведем в той же системе цилиндрических координат оптической схемы. Переменная rc неизвестна, а переменная zc (координата освещенной точки поверхности) легко определяется благодаря выбранной пространственной конфигурации оптической схемы.
– функции четырех переменных. Переменные jR, zR задаются независимо известным способом. Их отсчет ведем в той же системе цилиндрических координат оптической схемы. Переменная rc неизвестна, а переменная zc (координата освещенной точки поверхности) легко определяется благодаря выбранной пространственной конфигурации оптической схемы.
Из (3) получаем дифференциальные уравнения относительно неизвестного радиуса измеряемой поверхности в ее освещенной точке:
 ,
,  . (4)
. (4)
При этом левые части уравнений представляем как производные неявной функции радиуса rc, зависящей от переменных jc и zc и определяемой уравнением поверхности (1).
Запишем уравнения (4) в системе координат {r, j, z}, связанной с контролируемой поверхностью. Уравнения связи между системами координат имеют вид
r=rc, j=jc–jA, z=zc, (5)
где jA – угловая координата, связанная с поворотом контролируемой детали.
Она отсчитывается в системе координат оптического преобразователя, выбирается такой, чтобы в начале отсчета выполнялось условие j=0, и изменяется с поворотом поверхности при сканировании в соответствии с формулой
jA=jR–jconst, (6)
где jconst – постоянная величина угла, введенная для удобства расчетов.
Принимаем также, что величина угла jR изменяется в процессе сканирования от 0 до 2p или до минус 2p радиан в зависимости от направления сканирования.
Уравнения (4) переходят в следующие уравнения:
 ,
,  . (7)
. (7)
Функция вида r(jR, zR) является частным решением любого из них в отдельности. Из нее, используя (5) и очевидное соотношение
d=r sin jc, (8)
можно получить профиль радиуса r(j, z) в системе координат контролируемой поверхности, а из сетки таких профилей и изображение всей поверхности.
Для нахождения решения перейдем от уравнений (7) к уравнениям, содержащим дифференцирование только по независимым переменным jR и zR. При этом, в отличие от уравнений (7), их левые части представим как производные радиуса именно освещенной точки поверхности. Ее координаты в системе, связанной с контролируемой поверхностью, обозначим как (ra, ja, za). Они удовлетворяют уравнениям (7). В схеме устройства угловую координату рассматриваемой точки обозначим как a. При этом для радиусной и осевой координат этой точки в схеме устройства новые обозначения не вводятся, так как при выводе формул они не нужны. Подставляя в (5) и (6) вместо j величину ja и вместо jc величину a, имеем
ja=a–jR+jconst. (9)
Получим дифференциальные уравнения, связывающие искомый радиус ra контролируемой поверхности в ее освещенной точке с задаваемыми углом jR поворота этой поверхности вокруг оси OZ и смещением zR источника излучения.
Представим ra как сложную функцию:
ra=ra(ja, za), (10)
где ja=ja(jR, zR) и za=za (jR, zR). Согласно правилу вычисления производной сложной функции,
 . (11)
. (11)
Очевидно, что для точек на контролируемой поверхности
 ,
,  . (12)
. (12)
В соответствии с (9)
 . (13)
. (13)
Из (8) имеем
 , (14)
, (14)
тогда  . (15)
. (15)
Подставив первое из уравнений (7), а также полученное соотношение (15) в (11), имеем в результате дифференциальное уравнение следующего вида:
 . (16)
. (16)
Оно относится к нелинейным дифференциальным уравнениям в частных производных первого порядка. Так как в него входит только одна частная производная и к тому же выраженная в явном виде, то его можно считать и обыкновенным дифференциальным уравнением. Решая его при каком-либо постоянном zR, получаем функцию ra(jR, zR), от которой, используя (5), (6), (8) и (16), переходим к r(j, z) при заданном z=zR. Граничное условие имеет вид
ra(jR=0, zR=V)=ra(jR=2p, zR=V), (17)
где V – смещение источника излучения вдоль оси OZ от некоторого начального уровня.
При задании V должны выполняться два условия: 1) попадание зондирующего луча на контролируемую поверхность, 2) возможность детектирования этого луча фотоприемником после отражения его от контролируемой поверхности.
Условие (17) позволяет получить решение уравнения (16) в виде однозначной функции (радиальный профиль), что показали выполненные расчеты.
Так, авторами было получено аналитическое решение уравнения (16), линеаризованного по искомому r и информативным параметрам y и x при условии, что отклонения радиального профиля от круглости много меньше (менее 0,0001) средней величины его радиуса [4]. Нахождение этого решения доказало, что оно существует и единственно.
Для проверки полученных формул при значительных отклонениях от круглости, то есть когда данное условие не выполняется, авторы создали компьютерную модель оптической схемы измерений согласно рисунку 1 (при условии из [3]). При этом рассмотрена схема в плоскости, то есть контролируемая поверхность представлена цилиндром с направляющей, параллельной OZ. Модельный радиальный профиль представлен как синусоида, высоты которой отсчитывались в радиальном направлении от среднего радиуса. Решение получено численно. При этом использовался итерационный алгоритм, который сводился к последовательным вычислениям приближенных величин ra вдоль одного радиального профиля. В данном случае использовался известный метод вычислений Рунге–Кутты с точностью до четвертого порядка:
 ,
,
 ,
,
 ,
,
 ,
,
 , (18)
, (18)
где 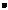 ‑ обозначение правой части уравнения (16); i – порядковый номер точки восстанавливаемого профиля, i=0, 1, 2, …, N, jR N=jR 0+2p, DjR= =jR i+1–jR i=2p/N. Отметим, что
‑ обозначение правой части уравнения (16); i – порядковый номер точки восстанавливаемого профиля, i=0, 1, 2, …, N, jR N=jR 0+2p, DjR= =jR i+1–jR i=2p/N. Отметим, что  , как и другие функции в правой части дифференциальных уравнений в этой работе, являются также и функциями информативных параметров y и x. Только для упрощения вида формул они не приведены в списке аргументов в скобках. Параметры y и x зависят от этих аргументов. Зависимости y(jR, zR) и x(jR, zR) использовались как исходные данные в расчетах по (18). При вращении контролируемой детали, как показано на рисунке 1, jR изменялся от 0 до 2p. Вычисление величин искомой функции в пределах одного радиального профиля представляло собой одну итерацию. Для исключения влияния дискретности зависимостей y(jR, zR) и x(jR, zR) внутри итерации было запрограммировано уменьшение шага дискретизации по jR в два раза, то есть удваивалось N, после чего расчеты по алгоритму (18) начинались вновь до тех пор, пока не выполнялось условие
, как и другие функции в правой части дифференциальных уравнений в этой работе, являются также и функциями информативных параметров y и x. Только для упрощения вида формул они не приведены в списке аргументов в скобках. Параметры y и x зависят от этих аргументов. Зависимости y(jR, zR) и x(jR, zR) использовались как исходные данные в расчетах по (18). При вращении контролируемой детали, как показано на рисунке 1, jR изменялся от 0 до 2p. Вычисление величин искомой функции в пределах одного радиального профиля представляло собой одну итерацию. Для исключения влияния дискретности зависимостей y(jR, zR) и x(jR, zR) внутри итерации было запрограммировано уменьшение шага дискретизации по jR в два раза, то есть удваивалось N, после чего расчеты по алгоритму (18) начинались вновь до тех пор, пока не выполнялось условие
 , (19)
, (19)
где j в данном случае – количество удвоений N. Величина (19) выбрана на два порядка большей, чем чувствительность модели к изменениям r.
 Нулевое приближение ra при jR=0 было взято как среднее арифметическое между d и L. Очередное приближение после каждой итерации могло быть выбрано, например, в согласии с известным методом стрельбы. Однако свойство устойчивости решения уравнения (16) позволило обойтись при этом выборе без дополнительных вычислений. Это свойство, обнаруженное авторами при компьютерном моделировании, проявляло себя в том, что при нахождении решения по алгоритму (18) отсчеты искомой функции ra все более приближались к решению уравнения (16) с каждым последующим шагом алгоритма (18). Компьютерное моделирование показало, что для достижения предела сходимости достаточно от двух до четырех итераций, причем сходимость процесса была экспоненциальной. Об устойчивости этого решения свидетельствовали и известные критерии устойчивости дифференциального уравнения, например, критерии Гурвица, Пригожина, Ляпунова. Результаты расчетов на разработанной компьютерной модели приведены на рисунке 3. Для более наглядного отображения сходимость показана как величина, равная
Нулевое приближение ra при jR=0 было взято как среднее арифметическое между d и L. Очередное приближение после каждой итерации могло быть выбрано, например, в согласии с известным методом стрельбы. Однако свойство устойчивости решения уравнения (16) позволило обойтись при этом выборе без дополнительных вычислений. Это свойство, обнаруженное авторами при компьютерном моделировании, проявляло себя в том, что при нахождении решения по алгоритму (18) отсчеты искомой функции ra все более приближались к решению уравнения (16) с каждым последующим шагом алгоритма (18). Компьютерное моделирование показало, что для достижения предела сходимости достаточно от двух до четырех итераций, причем сходимость процесса была экспоненциальной. Об устойчивости этого решения свидетельствовали и известные критерии устойчивости дифференциального уравнения, например, критерии Гурвица, Пригожина, Ляпунова. Результаты расчетов на разработанной компьютерной модели приведены на рисунке 3. Для более наглядного отображения сходимость показана как величина, равная
 , (20)
, (20)
где j – порядковый номер итерации, i имеет тот же смысл, что и в (18). После первой итерации величина (20) условно принята равной нулю. На рисунке 3 величина (20) показана отнесенной к одному периоду модельной синусоиды. Для нахождения величины (20), достигаемой при одной итерации, показанные на рисунке 3 величины надо умножить на количество K периодов модельной синусоиды. Результаты получены при следующих величинах параметров модели: d=7 мм, L=35 мм, средний радиус профиля R=10 мм, начальное значение N=10´K. При этом авторская модель имела чувствительность Dr=10–4 мкм к изменениям r. Максимальное количество отсчетов jR i в пределах одного периода модельной синусоиды, определенное программой, было 121. Тогда дискретность уже практически не сказывалась на результатах.
 Проведя переход, аналогичный проделанному, но уже от второго из уравнений (7), получаем:
Проведя переход, аналогичный проделанному, но уже от второго из уравнений (7), получаем:
 . (21)
. (21)
Для этого уравнения граничное условие находится из (16). Решение уравнения (21) дает профиль сечения измеряемой поверхности плоскостью, в которой перемещается падающий световой луч. Таким образом, ориентация профилей сечений измеряемой поверхности, являющихся решениями дифференциальных уравнений (16) или (21), определяется левыми частями этих уравнений.
Итак, уравнение (16) с граничными условиями (17) имеет единственное решение, когда контролируются зеркально отражающие поверхности вращения, имеющие значительные отклонения от круглости, сравнимые с их средним радиусом в том же радиальном профиле. С помощью описанного алгоритма удалось добиться точного восстановления радиального профиля в рамках использованной физической модели [3]. Ограничения на практике определяются областью применимости физической модели, а также возможностями оптического доступа к контролируемой поверхности и беспрепятственного прохода луча света, отраженного от контролируемой поверхности, до фотоприемника.
По выходной информации, накопленной на каждом шаге сканирования, восстанавливается форма всей поверхности. Один из способов – использование из двух полученных уравнений только уравнения (16). С его помощью на каждом шаге сканирования по оси OZ вычисляются высоты соответствующего радиального профиля. Для решения ограничиваются информацией, накопленной с участков контролируемой поверхности, которые лежат только на одном этом профиле. Однако использование дополнительно к (16) уравнения (21) на порядок уменьшало погрешность восстановления осевого профиля. Это было показано в поставленном авторами эксперименте [4], в ходе которого также проведена успешная проверка полученных формул.
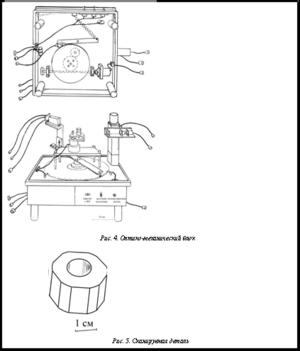
На рисунке 4 изображен оптико-механический блок лабораторного макета, созданного авторами для эксперимента. Пространственная конфигурация блока соответствует схеме на рисунке 1. По краям показаны электрические разъемы. Источник излучения – полупроводниковый лазер с длиной волны 0,78 мкм. Оценки предела суммарной погрешности: Dj=±0,5°, Dy=±0,1°, Dx=±13 мкм. В эксперименте использована специально изготовленная деталь (рис. 5) из алюминиевого сплава.
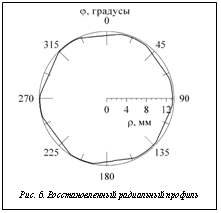 Ее сканируемая поверхность была обработана на токарном и шлифовальном станках и имела девятый класс шероховатости (Ra от 0,160 до 0,32 мкм включительно). Форма детали образована из цилиндра симметричным стачиванием шести граней. Диаметр – 27,8 мм, расстояние между противолежащими гранями – 26,4 мм. Для восстановления формы радиального профиля использованы алгоритмы и формулы, приведенные в данной работе. Величины параметров в эксперименте: d=10±0,05 мм, L=35 мм, N=300. Результаты показали (рис. 6), что восстановленный профиль в деталях совпадал со сканируемым, при этом погрешность восстановления не превышала 0,04 мм. Она максимум в 40 раз превосходила нижний предел погрешности Dr при идеальной кинематике блока, которая была оценена авторами в другой серии экспериментов на данном приборе, но с остановленной контролируемой деталью. При этом лабораторный макет работал так же, как если бы деталь вращалась, и в итоге получался виртуальный радиальный профиль, свободный от кинематических погрешностей. В результате сделано заключение о том, что погрешность измерений r определялась в эксперименте кинематическими погрешностями поворота контролируемой детали при сканировании.
Ее сканируемая поверхность была обработана на токарном и шлифовальном станках и имела девятый класс шероховатости (Ra от 0,160 до 0,32 мкм включительно). Форма детали образована из цилиндра симметричным стачиванием шести граней. Диаметр – 27,8 мм, расстояние между противолежащими гранями – 26,4 мм. Для восстановления формы радиального профиля использованы алгоритмы и формулы, приведенные в данной работе. Величины параметров в эксперименте: d=10±0,05 мм, L=35 мм, N=300. Результаты показали (рис. 6), что восстановленный профиль в деталях совпадал со сканируемым, при этом погрешность восстановления не превышала 0,04 мм. Она максимум в 40 раз превосходила нижний предел погрешности Dr при идеальной кинематике блока, которая была оценена авторами в другой серии экспериментов на данном приборе, но с остановленной контролируемой деталью. При этом лабораторный макет работал так же, как если бы деталь вращалась, и в итоге получался виртуальный радиальный профиль, свободный от кинематических погрешностей. В результате сделано заключение о том, что погрешность измерений r определялась в эксперименте кинематическими погрешностями поворота контролируемой детали при сканировании.
Таким образом, в статье приведены вывод расчетных формул и алгоритмы получения контурных картин криволинейных поверхностей способом триангуляции с использованием зеркально отраженного зондирующего пучка света. Полученные результаты успешно опробованы на разработанной компьютерной модели и в проведенном эксперименте.
Работа частично выполнялась в рамках НИР «Анализ и синтез световых полей в лазерной метрологии и технологии» (№ гос. регистрации 01910042666) в Самарском филиале Физического института РАН с 2002 по 2004 гг. Авторы благодарны Е. Воронцову за информационную поддержку.
Литература
1. Буцких В.А. Применение слепого разделения сигналов для подавления шумов спеклов в лазерной триангуляции / IX Всерос. молодеж. Самар. конкурс-конф. науч. работ по оптике и лазерной физике: сб. конкурс. докл. (9–13 ноября 2011 г., Самара). М.: ФИАН, 2011. С. 225–231.
2. Caulier Y., Spinnler K., Arnold M., et al. Automatic detection of surface and structural defects on reflecting workpieces / Photonik International. 2008. no. 2, pp. 30–32.
3. Born M., Wolf E. Principles of Optics: 7th (expanded) edition. Cambridge, UK: Cambridge University Press, 1999, 952 pp.
4. Заякин О.А. Информационно-измерительная система контроля деталей подшипников на основе двумерной лазерной триангуляции: дисс. … к-та тех. наук. Самара: СГТУ, 2005. 178 с.




 , падающий на поверхность, перпендикулярен плоскости YOZ и зеркально отражается относительно вектора нормали
, падающий на поверхность, перпендикулярен плоскости YOZ и зеркально отражается относительно вектора нормали  .
. регистрируется матричным фотоприемником, расположенным так, чтобы столбцы матрицы были параллельны оси x. С этой осью совмещается серединный столбец матрицы. Для поиска луча
регистрируется матричным фотоприемником, расположенным так, чтобы столбцы матрицы были параллельны оси x. С этой осью совмещается серединный столбец матрицы. Для поиска луча 
 ,
,  . (2)
. (2) ,
, , (3)
, (3) и
и  – функции четырех переменных. Переменные jR, zR задаются независимо известным способом. Их отсчет ведем в той же системе цилиндрических координат оптической схемы. Переменная rc неизвестна, а переменная zc (координата освещенной точки поверхности) легко определяется благодаря выбранной пространственной конфигурации оптической схемы.
– функции четырех переменных. Переменные jR, zR задаются независимо известным способом. Их отсчет ведем в той же системе цилиндрических координат оптической схемы. Переменная rc неизвестна, а переменная zc (координата освещенной точки поверхности) легко определяется благодаря выбранной пространственной конфигурации оптической схемы. ,
,  . (4)
. (4) ,
,  . (7)
. (7) . (11)
. (11) ,
,  . (12)
. (12) . (13)
. (13) , (14)
, (14) . (15)
. (15) . (16)
. (16) ,
, ,
, ,
, ,
, , (18)
, (18)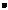 ‑ обозначение правой части уравнения (16); i – порядковый номер точки восстанавливаемого профиля, i=0, 1, 2, …, N, jR N=jR 0+2p, DjR= =jR i+1–jR i=2p/N. Отметим, что
‑ обозначение правой части уравнения (16); i – порядковый номер точки восстанавливаемого профиля, i=0, 1, 2, …, N, jR N=jR 0+2p, DjR= =jR i+1–jR i=2p/N. Отметим, что  , как и другие функции в правой части дифференциальных уравнений в этой работе, являются также и функциями информативных параметров y и x. Только для упрощения вида формул они не приведены в списке аргументов в скобках. Параметры y и x зависят от этих аргументов. Зависимости y(jR, zR) и x(jR, zR) использовались как исходные данные в расчетах по (18). При вращении контролируемой детали, как показано на рисунке 1, jR изменялся от 0 до 2p. Вычисление величин искомой функции в пределах одного радиального профиля представляло собой одну итерацию. Для исключения влияния дискретности зависимостей y(jR, zR) и x(jR, zR) внутри итерации было запрограммировано уменьшение шага дискретизации по jR в два раза, то есть удваивалось N, после чего расчеты по алгоритму (18) начинались вновь до тех пор, пока не выполнялось условие
, как и другие функции в правой части дифференциальных уравнений в этой работе, являются также и функциями информативных параметров y и x. Только для упрощения вида формул они не приведены в списке аргументов в скобках. Параметры y и x зависят от этих аргументов. Зависимости y(jR, zR) и x(jR, zR) использовались как исходные данные в расчетах по (18). При вращении контролируемой детали, как показано на рисунке 1, jR изменялся от 0 до 2p. Вычисление величин искомой функции в пределах одного радиального профиля представляло собой одну итерацию. Для исключения влияния дискретности зависимостей y(jR, zR) и x(jR, zR) внутри итерации было запрограммировано уменьшение шага дискретизации по jR в два раза, то есть удваивалось N, после чего расчеты по алгоритму (18) начинались вновь до тех пор, пока не выполнялось условие , (19)
, (19) Нулевое приближение ra при jR=0 было взято как среднее арифметическое между d и L. Очередное приближение после каждой итерации могло быть выбрано, например, в согласии с известным методом стрельбы. Однако свойство устойчивости решения уравнения (16) позволило обойтись при этом выборе без дополнительных вычислений. Это свойство, обнаруженное авторами при компьютерном моделировании, проявляло себя в том, что при нахождении решения по алгоритму (18) отсчеты искомой функции ra все более приближались к решению уравнения (16) с каждым последующим шагом алгоритма (18). Компьютерное моделирование показало, что для достижения предела сходимости достаточно от двух до четырех итераций, причем сходимость процесса была экспоненциальной. Об устойчивости этого решения свидетельствовали и известные критерии устойчивости дифференциального уравнения, например, критерии Гурвица, Пригожина, Ляпунова. Результаты расчетов на разработанной компьютерной модели приведены на рисунке 3. Для более наглядного отображения сходимость показана как величина, равная
Нулевое приближение ra при jR=0 было взято как среднее арифметическое между d и L. Очередное приближение после каждой итерации могло быть выбрано, например, в согласии с известным методом стрельбы. Однако свойство устойчивости решения уравнения (16) позволило обойтись при этом выборе без дополнительных вычислений. Это свойство, обнаруженное авторами при компьютерном моделировании, проявляло себя в том, что при нахождении решения по алгоритму (18) отсчеты искомой функции ra все более приближались к решению уравнения (16) с каждым последующим шагом алгоритма (18). Компьютерное моделирование показало, что для достижения предела сходимости достаточно от двух до четырех итераций, причем сходимость процесса была экспоненциальной. Об устойчивости этого решения свидетельствовали и известные критерии устойчивости дифференциального уравнения, например, критерии Гурвица, Пригожина, Ляпунова. Результаты расчетов на разработанной компьютерной модели приведены на рисунке 3. Для более наглядного отображения сходимость показана как величина, равная , (20)
, (20)
 . (21)
. (21) Ее сканируемая поверхность была обработана на токарном и шлифовальном станках и имела девятый класс шероховатости (Ra от 0,160 до 0,32 мкм включительно). Форма детали образована из цилиндра симметричным стачиванием шести граней. Диаметр – 27,8 мм, расстояние между противолежащими гранями – 26,4 мм. Для восстановления формы радиального профиля использованы алгоритмы и формулы, приведенные в данной работе. Величины параметров в эксперименте: d=10±0,05 мм, L=35 мм, N=300. Результаты показали (рис. 6), что восстановленный профиль в деталях совпадал со сканируемым, при этом погрешность восстановления не превышала 0,04 мм. Она максимум в 40 раз превосходила нижний предел погрешности Dr при идеальной кинематике блока, которая была оценена авторами в другой серии экспериментов на данном приборе, но с остановленной контролируемой деталью. При этом лабораторный макет работал так же, как если бы деталь вращалась, и в итоге получался виртуальный радиальный профиль, свободный от кинематических погрешностей. В результате сделано заключение о том, что погрешность измерений r определялась в эксперименте кинематическими погрешностями поворота контролируемой детали при сканировании.
Ее сканируемая поверхность была обработана на токарном и шлифовальном станках и имела девятый класс шероховатости (Ra от 0,160 до 0,32 мкм включительно). Форма детали образована из цилиндра симметричным стачиванием шести граней. Диаметр – 27,8 мм, расстояние между противолежащими гранями – 26,4 мм. Для восстановления формы радиального профиля использованы алгоритмы и формулы, приведенные в данной работе. Величины параметров в эксперименте: d=10±0,05 мм, L=35 мм, N=300. Результаты показали (рис. 6), что восстановленный профиль в деталях совпадал со сканируемым, при этом погрешность восстановления не превышала 0,04 мм. Она максимум в 40 раз превосходила нижний предел погрешности Dr при идеальной кинематике блока, которая была оценена авторами в другой серии экспериментов на данном приборе, но с остановленной контролируемой деталью. При этом лабораторный макет работал так же, как если бы деталь вращалась, и в итоге получался виртуальный радиальный профиль, свободный от кинематических погрешностей. В результате сделано заключение о том, что погрешность измерений r определялась в эксперименте кинематическими погрешностями поворота контролируемой детали при сканировании.