Независимая оценка качества образования с помощью современных контрольно-оценочных средств базируется на использовании однопараметрической дихотомической модели Раша [1]  , где qi – уровень подготовки i-го студента; βj – трудность j-го задания теста; pij – вероятность правильного выполнения i-м студентом j-го задания. Точность расчета латентных параметров qi (
, где qi – уровень подготовки i-го студента; βj – трудность j-го задания теста; pij – вероятность правильного выполнения i-м студентом j-го задания. Точность расчета латентных параметров qi ( ) зависит от того, насколько точно известны значения латентных параметров βj (
) зависит от того, насколько точно известны значения латентных параметров βj (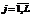 ), где N – число студентов, участвующих в тестировании; L – число заданий используемого при этом теста. Чем точнее определены значения βj, тем качественнее (с меньшей погрешностью) будут рассчитаны значения qi латентного параметра «уровень подготовки» студента. Оценки
), где N – число студентов, участвующих в тестировании; L – число заданий используемого при этом теста. Чем точнее определены значения βj, тем качественнее (с меньшей погрешностью) будут рассчитаны значения qi латентного параметра «уровень подготовки» студента. Оценки  и
и  латентных параметров βj и qi рассчитываются по результатам тестирования, которые представляются в виде дихотомической матрицы ответов X=(xij) [1]. Расчет оценок осуществляется численными методами на основе итерационных выражений [1, 2], полученных с использованием метода максимального правдоподобия.
латентных параметров βj и qi рассчитываются по результатам тестирования, которые представляются в виде дихотомической матрицы ответов X=(xij) [1]. Расчет оценок осуществляется численными методами на основе итерационных выражений [1, 2], полученных с использованием метода максимального правдоподобия.
Важным требованием к оценкам максимального правдоподобия  и
и  латентных параметров однопараметрической дихотомической модели Раша является наличие у них свойства состоятельности [3].
латентных параметров однопараметрической дихотомической модели Раша является наличие у них свойства состоятельности [3].
Состоятельность оценок 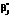 (
(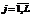 ) при неограниченном возрастании объема выборки участников тестирования N и конечном числе одинаковых по трудности (βj=0) заданий теста L доказана теоретически [4]. Затем было установлено, что оценки максимального правдоподобия
) при неограниченном возрастании объема выборки участников тестирования N и конечном числе одинаковых по трудности (βj=0) заданий теста L доказана теоретически [4]. Затем было установлено, что оценки максимального правдоподобия  и
и  латентных параметров однопараметрической дихотомической модели Раша являются состоятельными при N→∞ и L→∞.
латентных параметров однопараметрической дихотомической модели Раша являются состоятельными при N→∞ и L→∞.
Целью данной работы является экспериментальная проверка состоятельности оценок максимального правдоподобия  ,
,  латентных параметров однопараметрической дихотомической модели Раша при неограниченно возрастающем объеме выборки студентов N и числе заданий теста L.
латентных параметров однопараметрической дихотомической модели Раша при неограниченно возрастающем объеме выборки студентов N и числе заданий теста L.
Проверка проводилась на основе вычислительного эксперимента. В первой его части исследовалась зависимость оценок максимального правдоподобия латентных параметров «трудность задания» теста  и «уровень подготовки» студента
и «уровень подготовки» студента 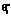 от размера матрицы результатов тестирования (матрицы ответов). Предполагалось, что распределения оценок
от размера матрицы результатов тестирования (матрицы ответов). Предполагалось, что распределения оценок  и
и 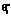 являются нормальными. В качестве их параметров были приняты значения, полученные при обработке модели нормативной дихотомической матрицы ответов размером 60´49 (первая строка таблицы 1). С их использованием на основе методики моделирования дихотомических матриц ответов, изложенной в [5], и созданного на ее основе алгоритма формировались модели дихотомических матриц размером 501´500, 1002´1000, 1503´1500, 2004´2006 и 2505´2505. Затем они обрабатывались программным комплексом RILP-1M [6], анализировались и сравнивались между собой оценки латентных параметров
являются нормальными. В качестве их параметров были приняты значения, полученные при обработке модели нормативной дихотомической матрицы ответов размером 60´49 (первая строка таблицы 1). С их использованием на основе методики моделирования дихотомических матриц ответов, изложенной в [5], и созданного на ее основе алгоритма формировались модели дихотомических матриц размером 501´500, 1002´1000, 1503´1500, 2004´2006 и 2505´2505. Затем они обрабатывались программным комплексом RILP-1M [6], анализировались и сравнивались между собой оценки латентных параметров  (
(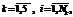 N1=501, N2=1002, N3=1503, N4=2004, N5=2505) и
N1=501, N2=1002, N3=1503, N4=2004, N5=2505) и  (
(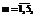
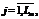 L1=500, L2=1000, L3=1500, L4=2006, L5=2505) при одинаковых значениях pi и pj, где pi - доля верных ответов i-го виртуального студента на все задания виртуального теста, соответствующего исходной модели матрицы; pi - доля верных ответов всех виртуальных студентов на j-е виртуальное задание этого же теста. Анализ полученных данных начинался со сравнения статистических параметров, характеризующих распределения оценок: выборочных средних
L1=500, L2=1000, L3=1500, L4=2006, L5=2505) при одинаковых значениях pi и pj, где pi - доля верных ответов i-го виртуального студента на все задания виртуального теста, соответствующего исходной модели матрицы; pi - доля верных ответов всех виртуальных студентов на j-е виртуальное задание этого же теста. Анализ полученных данных начинался со сравнения статистических параметров, характеризующих распределения оценок: выборочных средних  ,
, 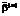 и оценок стандартных отклонений
и оценок стандартных отклонений  и
и  , которые представлены в таблице 1 в строках со 2-й по 6-ю. Из сравнения видно, что значения параметров достаточно близки, поэтому можно считать представительство результатов тестирования виртуальных студентов с разным уровнем подготовки и результатов выполнения виртуальных заданий с разным уровнем трудности во всех моделях матриц примерно одинаковым, что является свидетельством их нормативности.
, которые представлены в таблице 1 в строках со 2-й по 6-ю. Из сравнения видно, что значения параметров достаточно близки, поэтому можно считать представительство результатов тестирования виртуальных студентов с разным уровнем подготовки и результатов выполнения виртуальных заданий с разным уровнем трудности во всех моделях матриц примерно одинаковым, что является свидетельством их нормативности.
Таблица 1
Статистические параметры моделей матриц ответов
|
Размер матрицы
|
 , логит , логит
|
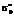 , логит , логит
|
 , логит , логит
|
 , логит , логит
|
|
60´49
|
0,043
|
1,33234
|
0,000
|
1,42348
|
|
501´500
|
0,047
|
1,41256
|
0,000
|
1,45031
|
|
1002´1000
|
0,051
|
1,44373
|
0,000
|
1,46848
|
|
1503´1500
|
0,046
|
1,40319
|
-0,003
|
1,40221
|
|
2004´2006
|
0,042
|
1,40026
|
-0,002
|
1,415
|
|
2505´2505
|
0,042
|
1,40048
|
-0,002
|
1,40784
|
Различия между собой кривых  , полученных при разных значениях Nk (
, полученных при разных значениях Nk ( ), и кривых
), и кривых 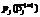 , рассчитанных при различных значениях Lm (
, рассчитанных при различных значениях Lm (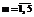 ), наиболее заметны на краях диапазонов изменения оценок
), наиболее заметны на краях диапазонов изменения оценок 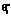 и
и  . На рисунке (а) представлены кривые
. На рисунке (а) представлены кривые  для интервала изменения
для интервала изменения  от 2 до 3 логит, а на рисунке (б) – для интервала от минус 3 до минус 4 логит. Из рисунка (а) видно, что значения
от 2 до 3 логит, а на рисунке (б) – для интервала от минус 3 до минус 4 логит. Из рисунка (а) видно, что значения 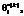 соответствующие одному и тому же значению pi, тем больше, чем меньше размер матрицы. Наибольшие расхождения наблюдаются для значений
соответствующие одному и тому же значению pi, тем больше, чем меньше размер матрицы. Наибольшие расхождения наблюдаются для значений 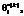 рассчитанных по матрицам 501´500 (кривая 1) и 2004´2006 (кривая 4). Например, при pi=0,86 эти различия составляют 2 %. Из рисунка (а) видно также, что значения
рассчитанных по матрицам 501´500 (кривая 1) и 2004´2006 (кривая 4). Например, при pi=0,86 эти различия составляют 2 %. Из рисунка (а) видно также, что значения  ,
, 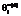 и
и 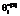 (кривые 3, 4, 5) практически одинаковы. Данный результат позволяет сделать вывод о том, что оценки латентных параметров
(кривые 3, 4, 5) практически одинаковы. Данный результат позволяет сделать вывод о том, что оценки латентных параметров  достигают своих предельных значений при размере матрицы результатов тестирования 1500´1500 и при его дальнейшем увеличении не изменяются. Анализ различий оценок
достигают своих предельных значений при размере матрицы результатов тестирования 1500´1500 и при его дальнейшем увеличении не изменяются. Анализ различий оценок  в диапазоне от минус 3 до минус 4 логит (рис. (б)) показывает, что по сравнению с рисунком (а) характер поведения оценок не меняется: для одинаковых pi большим по модулю значениям
в диапазоне от минус 3 до минус 4 логит (рис. (б)) показывает, что по сравнению с рисунком (а) характер поведения оценок не меняется: для одинаковых pi большим по модулю значениям  соответствуют матрицы меньших размеров. Иначе говоря, крутизна кривых
соответствуют матрицы меньших размеров. Иначе говоря, крутизна кривых  возрастает с увеличением размера матрицы.
возрастает с увеличением размера матрицы.
 На рисунке (в) изображены кривые
На рисунке (в) изображены кривые 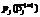 для моделей матриц разных объемов, позволяющие судить о зависимости оценок латентного параметра «трудность задания»
для моделей матриц разных объемов, позволяющие судить о зависимости оценок латентного параметра «трудность задания»  от размера матрицы. Как и для оценок
от размера матрицы. Как и для оценок  , при N, L≥1500 значения оценок
, при N, L≥1500 значения оценок  достигают своих предельных значений и с дальнейшим увеличением N, L не изменяются.
достигают своих предельных значений и с дальнейшим увеличением N, L не изменяются.
Таким образом, делаем следующие выводы:
1) с ростом объема выборки студентов N и числа заданий теста L оценки латентных параметров стремятся к предельным значениям, что является свидетельством их состоятельности;
2) оценки латентных параметров достигают предельных значений при N=1500 и L=1500 и с дальнейшим ростом N, L не изменяются, что позволяет говорить об их несмещенности;
3) с увеличением размера матрицы крутизна кривых  и
и 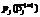 увеличивается.
увеличивается.
Во второй части вычислительного эксперимента полученные на моделях матриц ответов результаты проверялись на реальной матрице результатов тестирования ограниченного объема, в качестве которой использовалась матрица ответов М1 размером 51´50. Анализ гистограмм оценок латентных параметров 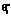 (
( ) и
) и  (
( ), рассчитанных с помощью программного комплекса RILP-1M, показал, что их распределения не противоречат гипотезе о нормальном законе распределения с параметрами mq=0,447 логит, σq=0,85293 логит, mβ=0,000 логит, σβ=0,80755 логит. С использованием этих статистических параметров были сформированы 4 модели нормативных дихотомических матриц ответов [5]: М2 – 503´503, М3 – 1003´1000, М4 – 1505´1507 и М5 – 2003´2006 в предположении нормального распределения значений оценок латентных параметров
), рассчитанных с помощью программного комплекса RILP-1M, показал, что их распределения не противоречат гипотезе о нормальном законе распределения с параметрами mq=0,447 логит, σq=0,85293 логит, mβ=0,000 логит, σβ=0,80755 логит. С использованием этих статистических параметров были сформированы 4 модели нормативных дихотомических матриц ответов [5]: М2 – 503´503, М3 – 1003´1000, М4 – 1505´1507 и М5 – 2003´2006 в предположении нормального распределения значений оценок латентных параметров  и
и  , рассчитанных по этим моделям матриц. В процессе обработки сформированных моделей матриц наряду с оценками латентных параметров
, рассчитанных по этим моделям матриц. В процессе обработки сформированных моделей матриц наряду с оценками латентных параметров 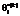 и
и  находились их выборочные средние арифметические
находились их выборочные средние арифметические  ,
, 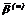 и оценки стандартных отклонений
и оценки стандартных отклонений  ,
,  . Нормативность исследуемых моделей матриц подтверждается данными таблицы 2.
. Нормативность исследуемых моделей матриц подтверждается данными таблицы 2.
Таблица 2
Статистические параметры матриц ответов, моделирующих матрицу М1
|
Матрица
|
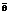 , логит , логит
|
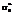 , логит , логит
|
 , логит , логит
|
 , логит , логит
|
|
51´50
|
0,447
|
0,85293
|
0,000
|
0,80755
|
|
503´503
|
0,466
|
0,86995
|
-0,009
|
0,82472
|
|
1003´1000
|
0,463
|
0,86537
|
-0,009
|
0,80942
|
|
1505´1507
|
0,464
|
0,86266
|
-0,009
|
0,81924
|
|
2003´2006
|
0,466
|
0,85647
|
-0,009
|
0,81161
|
Значения латентных параметров 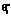 (i=
(i= ) и
) и  (j=
(j= ) исходной матрицы М1 представлены во вторых столбцах таблиц 3, 4, значения оценок
) исходной матрицы М1 представлены во вторых столбцах таблиц 3, 4, значения оценок  и
и  – в столбцах 3–6.
– в столбцах 3–6.

 По долям верных ответов pi первого столбца таблицы 3 находились соответствующие им значения
По долям верных ответов pi первого столбца таблицы 3 находились соответствующие им значения  (
(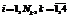 ) для каждого из четырех массивов, полученных по сформированным моделям матриц М2–М5. По значениям
) для каждого из четырех массивов, полученных по сформированным моделям матриц М2–М5. По значениям  определялись значения
определялись значения  , которые заносились в столбцы c 3-го по 6-й таблицы 3, а затем сравнивались с оценками
, которые заносились в столбцы c 3-го по 6-й таблицы 3, а затем сравнивались с оценками 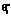 и между собой. Анализ полученных данных подтверждает полученные в первой части вычислительного эксперимента выводы: оценки латентных параметров
и между собой. Анализ полученных данных подтверждает полученные в первой части вычислительного эксперимента выводы: оценки латентных параметров  стремятся к предельным значениям, которые достигаются при N, L
стремятся к предельным значениям, которые достигаются при N, L 1500. Отличия их от исходных оценок
1500. Отличия их от исходных оценок 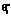 для большинства заданий (исключая из рассмотрения оценки
для большинства заданий (исключая из рассмотрения оценки 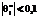 логит) составляют от 1 до 5 %, но могут достигать и 8 %. В столбцах 7 и 8 таблицы 3 показаны погрешности расчета оценок максимального правдоподобия латентных параметров модели Раша для исходной матрицы ответов М1 и для модели матрицы ответов М4 размером 1505´1507, а в столбце 9 – кратность отношения погрешностей. Видно, что погрешность расчета значений оценок
логит) составляют от 1 до 5 %, но могут достигать и 8 %. В столбцах 7 и 8 таблицы 3 показаны погрешности расчета оценок максимального правдоподобия латентных параметров модели Раша для исходной матрицы ответов М1 и для модели матрицы ответов М4 размером 1505´1507, а в столбце 9 – кратность отношения погрешностей. Видно, что погрешность расчета значений оценок 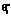 по матрице М4 снижается более чем в 5 раз. Таким образом, моделирование реальной матрицы ответов позволяет уточнить значения оценок латентных параметров
по матрице М4 снижается более чем в 5 раз. Таким образом, моделирование реальной матрицы ответов позволяет уточнить значения оценок латентных параметров 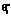 и не менее чем в 5 раз снизить погрешность их расчета.
и не менее чем в 5 раз снизить погрешность их расчета.
Аналогичный анализ оценок латентных параметров  (табл. 4), выполненный по описанной схеме, также подтверждает полученные в первой части вычислительного эксперимента выводы. За счет моделирования матрицы ответов значения оценок латентных параметров
(табл. 4), выполненный по описанной схеме, также подтверждает полученные в первой части вычислительного эксперимента выводы. За счет моделирования матрицы ответов значения оценок латентных параметров  могут быть уточнены на 1–10 %, в отдельных случаях – на 16 %, а погрешность их расчета снижена в 5 и более раз.
могут быть уточнены на 1–10 %, в отдельных случаях – на 16 %, а погрешность их расчета снижена в 5 и более раз.
На основе полученных результатов предложен следующий метод расчета оценок латентных параметров «трудность задания»  (метод калибровки заданий) и «уровень подготовки» студента
(метод калибровки заданий) и «уровень подготовки» студента 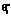 по матрицам результатов тестирования ограниченного объема:
по матрицам результатов тестирования ограниченного объема:
1) обрабатывают дихотомическую матрицу результатов тестирования ограниченного объема NH´LH программными средствами, базирующимися на использовании теории латентных переменных и однопараметрической дихотомической модели Раша;
2) выявляют тип и параметры распределений оценок латентных переменных 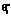 и
и  ;
;
3) формируют модель матрицы ответов размером 1500´1500 по найденным значениям параметров распределения оценок 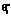 и
и  ;
;
4) обрабатывают модель найденной матрицы; сверяют параметры распределений полученных статистик  и
и  с параметрами распределений оценок
с параметрами распределений оценок 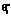 и
и  исходной матрицы ответов; если параметры сильно различаются, повторяют пункты 3 и 4 до тех пор, пока эти различия не станут приемлемыми;
исходной матрицы ответов; если параметры сильно различаются, повторяют пункты 3 и 4 до тех пор, пока эти различия не станут приемлемыми;
5) по значениям долей pi верных ответов студентов на все задания и долей pj верных ответов всех студентов на задания теста, которые соответствуют найденным оценкам 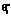 и
и  , находят наиболее близкие к ним значения pi0 и pj0, рассчитанные по сформированной модели дихотомической матрицы 1500´1500;
, находят наиболее близкие к ним значения pi0 и pj0, рассчитанные по сформированной модели дихотомической матрицы 1500´1500;
6) выбирают из массивов значений  и
и  оценки
оценки  и
и  по значениям pi0 и pj0 (
по значениям pi0 и pj0 (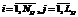 );
);
7) принимают найденные оценки  ,
,  и погрешности их расчета в качестве значений латентных параметров qi, βj и погрешностей их расчета.
и погрешности их расчета в качестве значений латентных параметров qi, βj и погрешностей их расчета.
Таким образом, результаты вычислительного эксперимента подтверждают полученный теоретическим путем вывод о состоятельности оценок максимального правдоподобия латентных параметров βj «трудность задания» теста и qi «уровень подготовки» студента при больших объемах выборки студентов N и большом количестве заданий теста L. Установлено, что оценки 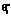 ,
,  достигают своих предельных значений
достигают своих предельных значений  ,
,  при N=L=1500.
при N=L=1500.
Предложенный метод калибровки заданий теста по матрицам результатов тестирования ограниченного объема позволит существенно повысить ее точность и снизить погрешности оценки результатов образовательной деятельности.
Литература
1. Нейман Ю.М., Хлебников В.А. Введение в теорию моделирования и параметризации педагогических тестов. М., 2000. 168 с.
2. Елисеев И.Н. Теоретические основы алгоритма расчета латентных переменных программным комплексом RILP-1M // Программные продукты и системы. 2011. № 2 (94). С. 67–71.
3. Елисеев И.Н., Шрайфель И.С. Доказательство несостоятельности стандартных оценок латентных параметров дихотомической модели Раша // Изв. вузов: Электромеханика, 2012. № 1. С. 85–96.
4. Елисеев И.Н., Шрайфель И.С. Модель оценивания латентных параметров дихотомической модели Раша // Изв. вузов. Северо-Кавказский регион: Технические науки. 2011. № 6. С. 37–46.
5. Елисеев И.Н. Модель дихотомической матрицы результатов тестирования // Программные продукты и системы. 2011. № 3. С. 80–86.
6. Елисеев И.Н., Елисеев И.И., Фисунов А.В. Програм- мный комплекс RILP-1 // Программные продукты и системы. 2009. № 2. С. 178–181.



 , где qi – уровень подготовки i-го студента; βj – трудность j-го задания теста; pij – вероятность правильного выполнения i-м студентом j-го задания. Точность расчета латентных параметров qi (
, где qi – уровень подготовки i-го студента; βj – трудность j-го задания теста; pij – вероятность правильного выполнения i-м студентом j-го задания. Точность расчета латентных параметров qi ( ) зависит от того, насколько точно известны значения латентных параметров βj (
) зависит от того, насколько точно известны значения латентных параметров βj (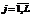 ), где N – число студентов, участвующих в тестировании; L – число заданий используемого при этом теста. Чем точнее определены значения βj, тем качественнее (с меньшей погрешностью) будут рассчитаны значения qi латентного параметра «уровень подготовки» студента. Оценки
), где N – число студентов, участвующих в тестировании; L – число заданий используемого при этом теста. Чем точнее определены значения βj, тем качественнее (с меньшей погрешностью) будут рассчитаны значения qi латентного параметра «уровень подготовки» студента. Оценки  и
и  латентных параметров βj и qi рассчитываются по результатам тестирования, которые представляются в виде дихотомической матрицы ответов X=(xij) [1]. Расчет оценок осуществляется численными методами на основе итерационных выражений [1, 2], полученных с использованием метода максимального правдоподобия.
латентных параметров βj и qi рассчитываются по результатам тестирования, которые представляются в виде дихотомической матрицы ответов X=(xij) [1]. Расчет оценок осуществляется численными методами на основе итерационных выражений [1, 2], полученных с использованием метода максимального правдоподобия. и
и 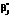 (
( и «уровень подготовки» студента
и «уровень подготовки» студента 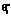 от размера матрицы результатов тестирования (матрицы ответов). Предполагалось, что распределения оценок
от размера матрицы результатов тестирования (матрицы ответов). Предполагалось, что распределения оценок  и
и  (
(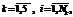 N1=501, N2=1002, N3=1503, N4=2004, N5=2505) и
N1=501, N2=1002, N3=1503, N4=2004, N5=2505) и  (
(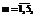
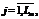 L1=500, L2=1000, L3=1500, L4=2006, L5=2505) при одинаковых значениях pi и pj, где pi - доля верных ответов i-го виртуального студента на все задания виртуального теста, соответствующего исходной модели матрицы; pi - доля верных ответов всех виртуальных студентов на j-е виртуальное задание этого же теста. Анализ полученных данных начинался со сравнения статистических параметров, характеризующих распределения оценок: выборочных средних
L1=500, L2=1000, L3=1500, L4=2006, L5=2505) при одинаковых значениях pi и pj, где pi - доля верных ответов i-го виртуального студента на все задания виртуального теста, соответствующего исходной модели матрицы; pi - доля верных ответов всех виртуальных студентов на j-е виртуальное задание этого же теста. Анализ полученных данных начинался со сравнения статистических параметров, характеризующих распределения оценок: выборочных средних  ,
, 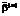 и оценок стандартных отклонений
и оценок стандартных отклонений  и
и  , которые представлены в таблице 1 в строках со 2-й по 6-ю. Из сравнения видно, что значения параметров достаточно близки, поэтому можно считать представительство результатов тестирования виртуальных студентов с разным уровнем подготовки и результатов выполнения виртуальных заданий с разным уровнем трудности во всех моделях матриц примерно одинаковым, что является свидетельством их нормативности.
, которые представлены в таблице 1 в строках со 2-й по 6-ю. Из сравнения видно, что значения параметров достаточно близки, поэтому можно считать представительство результатов тестирования виртуальных студентов с разным уровнем подготовки и результатов выполнения виртуальных заданий с разным уровнем трудности во всех моделях матриц примерно одинаковым, что является свидетельством их нормативности. , логит
, логит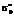 , логит
, логит , логит
, логит , логит
, логит , полученных при разных значениях Nk (
, полученных при разных значениях Nk ( ), и кривых
), и кривых 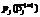 , рассчитанных при различных значениях Lm (
, рассчитанных при различных значениях Lm (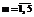 ), наиболее заметны на краях диапазонов изменения оценок
), наиболее заметны на краях диапазонов изменения оценок  от 2 до 3 логит, а на рисунке (б) – для интервала от минус 3 до минус 4 логит. Из рисунка (а) видно, что значения
от 2 до 3 логит, а на рисунке (б) – для интервала от минус 3 до минус 4 логит. Из рисунка (а) видно, что значения 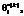 соответствующие одному и тому же значению pi, тем больше, чем меньше размер матрицы. Наибольшие расхождения наблюдаются для значений
соответствующие одному и тому же значению pi, тем больше, чем меньше размер матрицы. Наибольшие расхождения наблюдаются для значений  ,
, 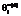 и
и 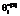 (кривые 3, 4, 5) практически одинаковы. Данный результат позволяет сделать вывод о том, что оценки латентных параметров
(кривые 3, 4, 5) практически одинаковы. Данный результат позволяет сделать вывод о том, что оценки латентных параметров  На рисунке (в) изображены кривые
На рисунке (в) изображены кривые  от размера матрицы. Как и для оценок
от размера матрицы. Как и для оценок  ) и
) и  ), рассчитанных с помощью программного комплекса RILP-1M, показал, что их распределения не противоречат гипотезе о нормальном законе распределения с параметрами mq=0,447 логит, σq=0,85293 логит, mβ=0,000 логит, σβ=0,80755 логит. С использованием этих статистических параметров были сформированы 4 модели нормативных дихотомических матриц ответов [5]: М2 – 503´503, М3 – 1003´1000, М4 – 1505´1507 и М5 – 2003´2006 в предположении нормального распределения значений оценок латентных параметров
), рассчитанных с помощью программного комплекса RILP-1M, показал, что их распределения не противоречат гипотезе о нормальном законе распределения с параметрами mq=0,447 логит, σq=0,85293 логит, mβ=0,000 логит, σβ=0,80755 логит. С использованием этих статистических параметров были сформированы 4 модели нормативных дихотомических матриц ответов [5]: М2 – 503´503, М3 – 1003´1000, М4 – 1505´1507 и М5 – 2003´2006 в предположении нормального распределения значений оценок латентных параметров 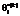 и
и  находились их выборочные средние арифметические
находились их выборочные средние арифметические  ,
, 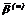 и оценки стандартных отклонений
и оценки стандартных отклонений  ,
,  . Нормативность исследуемых моделей матриц подтверждается данными таблицы 2.
. Нормативность исследуемых моделей матриц подтверждается данными таблицы 2.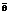 , логит
, логит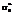 , логит
, логит , логит
, логит , логит
, логит ) и
) и  ) исходной матрицы М1 представлены во вторых столбцах таблиц 3, 4, значения оценок
) исходной матрицы М1 представлены во вторых столбцах таблиц 3, 4, значения оценок 

 (
(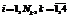 ) для каждого из четырех массивов, полученных по сформированным моделям матриц М2–М5. По значениям
) для каждого из четырех массивов, полученных по сформированным моделям матриц М2–М5. По значениям  определялись значения
определялись значения  1500. Отличия их от исходных оценок
1500. Отличия их от исходных оценок 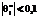 логит) составляют от 1 до 5 %, но могут достигать и 8 %. В столбцах 7 и 8 таблицы 3 показаны погрешности расчета оценок максимального правдоподобия латентных параметров модели Раша для исходной матрицы ответов М1 и для модели матрицы ответов М4 размером 1505´1507, а в столбце 9 – кратность отношения погрешностей. Видно, что погрешность расчета значений оценок
логит) составляют от 1 до 5 %, но могут достигать и 8 %. В столбцах 7 и 8 таблицы 3 показаны погрешности расчета оценок максимального правдоподобия латентных параметров модели Раша для исходной матрицы ответов М1 и для модели матрицы ответов М4 размером 1505´1507, а в столбце 9 – кратность отношения погрешностей. Видно, что погрешность расчета значений оценок  и
и  по значениям pi0 и pj0 (
по значениям pi0 и pj0 (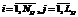 );
); ,
,  и погрешности их расчета в качестве значений латентных параметров qi, βj и погрешностей их расчета.
и погрешности их расчета в качестве значений латентных параметров qi, βj и погрешностей их расчета.