Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Анализ критических точек отказоустойчивости вычислительной среды планетарного типа
Аннотация:
Abstract:
| Авторы: Коганов А.В. (koganow@niisi.msk.ru) - НИИСИ РАН, г. Москва, кандидат физико-математических наук, Сазонов А.Н. (sazonov@rg.ru) - ООО «Дойчебанк», г. Москва | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 12621 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
ременном обществе быстро возрастает значение распределенных систем информационного и вычислительного назначения. С увеличением сложности и объема этих систем растет влияние аварийных факторов на их функционирование. В правильно разработанной системе выход из строя относительно малого числа функциональных элементов не приводит к остановке системы, а только увеличивает нагрузку на оставшиеся элементы. Это позволяет осуществить частичный или полный ремонт отказавших узлов, продлив время безотказной работы системы в целом. Возникает задача обеспечения достаточно малой вероятности выхода системы из строя за предполагаемый срок эксплуатации. Поскольку выход узлов системы их строя обычно обусловлен неконтролируемыми факторами, для решения указанной задачи надо подбирать подходящую интенсивность ремонтных работ и систему переназначения задач на исправных элементах. Решение этой задачи для реальных систем требует построения соответствующих математических моделей и машинного эксперимента. Разработке соответствующего программного комплекса и расчету некоторых модельных ситуаций посвящена данная работа. Разработанные программы позволяют исследовать любую систему распределенной обработки информации, если она может быть описана графом связи функциональных элементов разных типов и вероятностями их отказов и восстановления за один цикл работы системы. Но модельные расчеты проводились на схеме с характерной для вычислительных систем структурой: связанные между собой центральные вычислительные машины, каждая из которых управляет своим набором периферийных устройств (датчиков, эффекторов или вспомогательных вычислителей). Подобные системы по очевидной аналогии названы планетарными. Задача может быть решена на такой системе, если имеется набор центральных машин («звезд»), имеющих в совокупности нужный набор периферийных устройств («планет»). Решение задачи для произвольного графа требует значительно больших вычислительных ресурсов и времени счета. Полученные результаты позволили выявить зависимость показателей объема системы и ее надежности в форме непараметрических кривых и в виде регрессионных моделей. Особый интерес представляют результаты об эффективности быстрого ремонта, когда часть элементов удается восстановить еще до начала очередного цикла решения задачи. Без изменения вероятности успешного восстановления эффективность дублирования возрастает более чем в два раза (по критерию значения критической вероятности отказа). Вычислительные среды с разрушением и восстановлением Обобщенная модель вычислительной среды (ВС) рассматривается в виде направленного графа с помеченными вершинами, где метки (цвета) вершин соответствуют типам узлов, а дуги – односторонним каналам передачи данных. Каждая из задач, выполняющихся на ВС, может занимать один или несколько узлов. Следовательно, можно рассматривать модель задачи (МЗ), основанную на модели ВС (МВС). Соответственно, МЗ также будет направленным графом с мечеными вершинами. Для возможности выполнения задачи на данной ВС необходимо, чтобы МЗ была изоморфна какому-либо подграфу МВС. В случае выхода из строя компонентов ВС оставшаяся работоспособной часть системы называется разрушенной ВС (РВС). Вследствие того что задача может использовать не все узлы исходной ВС, а также из-за возможности дублирования элементов, в некоторых случаях исходная задача сможет выполняться и на РВС. Для исследования отказоустойчивости МЗ может быть выбрана так, чтобы ее граф совпадал с графом исходной ВС. Такая МЗ называется полной (ПМЗ). В этом случае работа задачи на РВС (при условии, что граф РВС не совпадает с графом ВС) будет возможна, только если в ВС имело место дублирование узлов и существуют все необходимые задаче дуги графа РВС. Для возможности выполнения задачи на ВС необходимо ассоциировать каждую вершину МЗ с вершиной МВС того же типа так, чтобы при этом в полученном образе задачи на графе МВС существовали все дуги, соответствующие дугам на графе МЗ. Рассмотрим случай, когда несколько однотипных вершин графа МЗ могут быть ассоциированы с одной и той же вершиной МВС того же типа. При этом предполагается, что локальные пересылки данных с одного узла ВС на самого себя всегда возможны. Под разложимостью графа МЗ на граф МВС понимается возможность указанного отображения вершин этих графов. Общий алгоритм моделирования работы ВС. Алгоритм 1: для направленного раскрашенного графа ВС произвольного вида моделирование разрушения и восстановления производится следующим образом. 1. Задается начальный граф ВС. 2. Задается вероятность разрушения одного узла Pd. 3. Задается вероятность починки одного узла Pf (в общем случае Pf и Pd могут быть разными для разных узлов или разных типов узлов). 4. Задается количество итераций разрушения Ni. 5. Начальный граф РВС полагается равным графу ВС. 6. Для каждого i=1…Ni производятся следующие действия: a) разрушение (для каждого узла РВС производится испытание Бернулли с вероятностью успеха Pd; в случае успеха узел и все инцидентные ему дуги исключаются из графа РВС); b) восстановление (для всех узлов исходной ВС, не содержащихся в графе РВС, производится испытание Бернулли с вероятностью успеха Pf; в случае успеха узел и все инцидентные ему дуги, идущие к другим узлам РВС, добавляются в граф РВС); c) производится поиск разложения ПМЗ на РВС: если разложение не найдено, эксперимент оканчивается неудачей, и номер текущей итерации i называется временем отказа. Примечание: Шаги 6a и 6b могут производиться в обратной последовательности. 7. Если все итерации не окончились неудачей, эксперимент считается удачным, время отказа полагается равным количеству итераций. Задача поиска подграфа, изоморфного данному, для нераскрашенных графов является NP-полной (см.: Cook S.A. The complexity of theorem-proving procedures // Annual ACM Symposium on Theory of Computing. 1971). Нераскрашенный граф является частным случаем раскрашенного (одноцветного), и, таким образом, задача для раскрашенных графов также является NP-полной. Поиск разложения МЗ на РВС может быть полиномиально сведен к задаче поиска подграфа, изоморфного данному, при помощи добавления специальных вершин к графам МЗ и РВС (см.: А.В. Коганов, А.Н. Сазонов. Анализ отказоустойчивости вычислительной среды планетарного типа. // Сб. науч. тр. М.-Ижевск. 2006). Таким образом, общий алгоритм моделирования достаточно ресурсоемок. Кроме того, для графов ВС произвольного вида неоднозначна оценка их сложности. Данный эксперимент при Pf<1 и Pd>0 не может закончиться успехом при бесконечном числе итераций, так как путем восстановления не может быть получено больше вершин, чем существовало в графе исходной ВС, а в силу вероятностного характера процесса разрушения на бесконечности будет существовать итерация, в которой граф РВС будет вырожденным. Моделирование планетарной ВС с разрушением и восстановлением Планетарная ВС (ПВС) – ВС, граф которой двунаправленный, состоящий из центральных элементов (звезд), с каждым из которых связаны серверные элементы разных типов (планеты). Планетарная система – подграф ПВС, состоящий из одной звезды и всех ее планет. Звезды между собой связаны полным графом. Цвета всех звезд одинаковы. Цвета планет могут отличаться, однако никогда не совпадают с цветом звезд. Граф ПМЗ для ПВС, соответственно, совпадает с графом ПВС. Для ПВС был задан процесс генерации вероятностного типа с тремя основными характеристиками: S – количество звезд; C – количество цветов; K – среднее количество планет каждого цвета у каждой звезды. Число планет у звезды равно KC. При генерации ПВС каждая планета получает цвет как реализацию равновероятного испытания Бернулли на множестве цветов 1,…,С. Модификация алгоритма 1 для моделирования ПВС. Алгоритм 2. В силу свойств графа ПВС процесс поиска разложения полной модели планетарной задачи (ПМПЗ) на разрушенную ПВС (РПВС) сводится к поиску для каждой звезды из МЗ звезды-образа в РПВС, такой что множество цветов планет исходной звезды не менее аналогичного множества для ее образа. При этом количество планет одинакового цвета у звезды в РПВС несущественно. Если для всех звезд ПМПЗ соответствующая звезда в графе РПВС найдена, то задача может быть выполнена на РПВС. Эта задача значительно проще, чем решение общей задачи поиска разложения произвольного графа МЗ на граф РВС. В остальном моделирование работы для ПВС аналогично моделированию для произвольной ВС с использованием алгоритма 1. Определение ПВС позволяет произвести несколько оптимизаций расчетов: · в случае ПВС не требуется учета соответствия дуг в графе задачи и подграфе ПВС, достаточно лишь наличие планет нужных цветов; · при создании, разрушении и восстановлении ПВС достаточно для каждой звезды задать (уменьшить или увеличить соответственно) количество планет каждого цвета в соответствии с результатами испытаний Бернулли. Модифицированный алгоритм 1 для случая ПВС назовем алгоритмом 2. Алгоритм поиска критической вероятности разрушения Вычисление среднего времени отказа ПВС. Алгоритм 3. Для проведения статистического эксперимента вычисления среднего времени отказа дополнительно задается параметр Ne – количество экспериментов для одного набора параметров S, C, K, Pd, Pf, Ni. Здесь S, C, K – параметры генерации графа в каждом эксперименте; Pd, Pf, Ni – параметры эксперимента. Далее с применением алгоритма 2 Ne раз может быть вычислено среднее время отказа системы Md, а также количество удачных экспериментов F. Уделим основное внимание параметру F (finish), равному количеству экспериментов, в которых отказ не был получен на всех итерациях (то есть число испытаний, в которых ВС «дошла до финиша»). Критической вероятностью разрушения для заданных параметров S, C, K, Pf, Ni, Ne и некоторого eÎ(0,1) называется эмпирическое значение Pc, такое что при меньших либо равных значениях Pd выполняется F/Ne>(1-e): Pc=max{P|Pd≤P=>F/Ne>(1-e)}. В этом случае при Pd≤Pc вероятность неуспеха ниже e. Статистический поиск критической вероятности разрушения ПВС. Алгоритм 4. 1) Задаются параметры S, C, K, Pf, Ni, Ne, e, Pdmin, Pdmax, DPd, где Pdmin – минимальная вероятность разрушения для поиска, Pdmax – максимальная вероятность, DP – шаг изменения вероятности. 2) Для каждой вероятности Pdi=Pdmax,Pdmax- -DPd, Pdmax-2DPd, … Pdmax-nDPd, где n такое, что Pdmax-Pdmin-DPd 3) Если, начиная с некоторого эксперимента k, получаемые количества успехов в экспериментах Fi (при вероятности разрушения Pdi=Pdmax-iDPd) таковы, что Fi/Ne>(1-e) для всех iÎ[k, n], критическая вероятность разрушения Pc полагается равной Pd=Pdmax-kDPd. Если такого k не найдено, Pc полагается равным нулю. Алгоритм 5. Для исследования зависимости Pc от S и Pf применяется варьирование параметров алгоритма 4. 1) S последовательно полагается равным Smin, Smin+1, …, Smax. 2) При заданном S Pf последовательно полагается равным Pfmax, Pfmax-DPf, Pfmax-2DPf, …, Pfmin. 3) При полученных S и Pf производится статистический поиск критической вероятности разрушения с использованием алгоритма 4. Также могут проводиться эксперименты с измененным порядком следования этапов разрушения и восстановления вершин графа РПВС. Так как каждый из алгоритмов 2-5 решает часть задачи следующего и характер всех этих алгоритмов переборный, вычислительная сложность задачи поиска критической вероятности даже для ПВС достаточно высока. В случае произвольной ВС для разложения МЗ приходилось бы использовать также сложный алгоритм из класса NP, что еще более усложняло бы сбор статистики при разных параметрах экспериментов. Эксперименты с восстановлением после разрушения. Эксперимент 1 (рис. 1). S=1,…,20; C=20; K=20; Ni=500; Ne=200; e=0,01; Pdmax=0,95; Pdmin=0,05; DPd=0,05 Pfmax=0,5; Pfmin=0,2; DPf=0,05 Уравнение линейной регрессии: Pc=0,039S+ +1,198Pf-0,536 Таблица 1 Доверительные интервалы по уровню 5% для эксперимента с восстановлением после разрушения
Эксперимент 2 (детализированный) (рис. 2). Параметры эксперимента: S=1,…,20; C=20; K=20; Ni=500; Ne=200; e=0,01; Pdmax=0,98; Pdmin=0,04; DPd=0,02 Pfmax=0,6; Pfmin=0,2; DPf=0,05
Таблица 2 Доверительные интервалы по уровню 5% для детализированного эксперимента с восстановлением после разрушения
Эксперимент с разрушением после восстановления. Эксперимент 3 (рис. 3). S=1,…,20; C=20; K=20; Ni=500; Ne=200; e=0,01; Pdmax=0,95; Pdmin=0,05; DPd=0,05 Pfmax=0,5; Pfmin=0,2; DPf=0,05 Уравнение линейной регрессии: Pc=0,017S+ +0,355Pf-0,175 Таблица 3 Доверительные интервалы по уровню 5% при разрушении после восстановления
Анализируя полученные данные, отметим, что для экспериментов получены следующие уравнения линейной регрессии: эксперимент 1: Pc=0,04S+1,2Pf-0,54; эксперимент 2: Pc=0,05S+1,19Pf-0,59; эксперимент 3: Pc=0,02S+0,36Pf-0,17. Коэффициенты первых двух уравнений практически идентичны. Разница коэффициентов может объясняться как конечностью эксперимента, так и различной точностью экспериментов (разными DPd, Pdmin, Pdmax, Pfmax). Параметры эксперимента 3 совпадают с параметрами эксперимента 1, за исключением порядка следования этапов разрушения и восстановления. Однако коэффициенты регрессионных уравнений для экспериментов 1 и 3 отличаются гораздо сильнее, чем для экспериментов 1 и 2: эксперимент 1: Pc=0,039 S+1,198 Pf - 0,536; эксперимент 3: Pc=0,017 S+0,355 Pf - 0,175. Напомним, что в эксперименте 1 на каждой итерации сначала проводилось разрушение, затем восстановление РВС, после чего предпринималась попытка нахождения разложения ПМПЗ на РВС. В эксперименте 3 порядок был иным: восстановление РВС, разрушение, разложение ПМПЗ на РВС. В итоге при изменении последовательности этапов разрушения и восстановления коэффициент при S уменьшился в более чем в 2 раза, коэффициент при Pf уменьшился более чем в 3 раза, свободный член уменьшился более чем в 3 раза. Таким образом, обращаясь к предметной области задачи, в условиях проведенных экспериментов ремонт системы непосредственно после разрушения и перед очередным циклом работы позволяет увеличить надежность системы более чем в 2 раза (по критерию значения критической вероятности отказа). Следует отметить также, что в эксперименте 3 max(Pc)=0,4, а в эксперименте 1 max(Pc)=0,95, что равно Pdmax, то есть это максимально возможное значение при заданных параметрах эксперимента. Аналогично и в эксперименте 2 max(pc)=0,98==Pdmax. Таким образом, в экспериментах 1 и 2 max(Pc) достигло максимума, в то время как в эксперименте 2 Pc не достигло и его половины. Это еще раз подчеркивает, что в условиях данных экспериментов починка сразу после разрушения дает очевидную выгоду для увеличения надежности системы. При положительной вероятности разрушения и вероятности починки менее 1 с увеличением количества итераций Ni значение Pc стремятся к нулю при любых значениях Pf и S. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=330&page=article |
Версия для печати Выпуск в формате PDF (2.31Мб) |
| Статья опубликована в выпуске журнала № 3 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Компьютерная технология проектирования перестраиваемых нерекурсивных фильтров
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Анализ российского и зарубежного рынков программных продуктов
- Общедоступные математические САПР для персональных компьютеров класса IBM PC
- Системное тестирование программных изделий
Назад, к списку статей



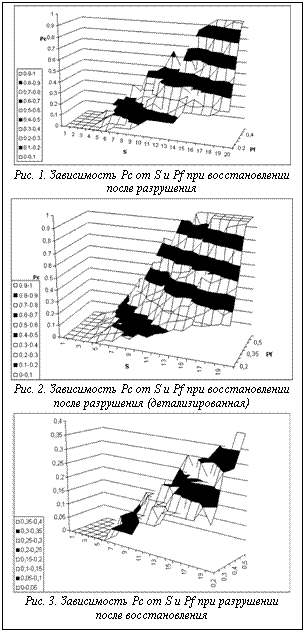 Уравнение линейной регрессии: Pc=0,045S+ +1,186Pf-0,59
Уравнение линейной регрессии: Pc=0,045S+ +1,186Pf-0,59