В научных трудах рассматривались вопросы отображения программ на архитектуру вычислительной системы [1]. В данной работе решается обратная задача – отображение архитектуры на прикладные программы. Она возникает тогда, когда встает проблема выбора вычислительной системы для конкретных задач. Рассмотрим форма- лизацию выбора вычислительной системы для решения научно-технических задач.

Среди высокопроизводительных вычислительных систем наибольшее распространение получили кластерные системы. Сегодня типичная высокопроизводительная кластерная система состоит из узлов, объединенных несколькими сетями: коммуникационной, транспортной, управляющей, служебной. Узлы вместе с коммуникационной сетью образуют вычислительное поле. Коммуникационная сеть используется для обмена данными между вычислительными узлами во время расчетов. Транспортные сети используются для передачи данных между вычислительным полем и файловой системой. Управляющая сеть используется для организации процесса вычислений, например, для загрузки параллельных программ. Служебная сеть предназначена для управления аппаратурой. Самые высокие требования по производительности предъявляются к коммуникационной сети, поэтому они обычно имеют высокую пропускную способность и низкую латентность. Примером коммуникационных сетей являются сети, построенные по технологии Infiniband. Остальные сети чаще всего реализуются с помощью технологии Ethernet. Для экономии места или средств в вычислительной системе некоторые сети могут объединяться. Вычислительный узел содержит несколько многоядерных процессоров (обычно два), работающих на общей или псевдообщей памяти. Для увеличения производительности при выполнении сильно параллельных задач в узле могут устанавливаться ускорители (обычно от 1 до 4).

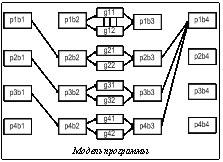
Модели программы и вычислительной системы

Рассмотрим наиболее широко используемую синхронную модель программирования SPMD, в которой один код параллельной программы выполняется на всех ядрах. Представим программу в виде блоков операций. Блоки операций могут быть вычислительными операциями, коммуникационными и операциями ввода-вывода. Рассмотрим такую модель выполнения программы на кластере, при которой блоки не перемещаются между узлами. Обозначим блок вычислительных операций bi. Основные данные для блока bi находятся в памяти узла. После выполнения блока bi возможен обмен данными.

Рассмотрим вычислительное поле, состоящее из вычислительных узлов, объединенных коммуникационной сетью. Вычислительный узел состоит из Np процессоров с общей памятью и Ng ускорителей. Обозначим время выполнения блока bi на процессоре pj как Tbipj, на ускорителе gk – как Tbigk.

На рисунке приведена модель выполнения программы на четырех однопроцессорных узлах (p1–p4), на каждом их которых установлено по два графических ускорителя (g11–g42). После выполнения блока b1 на всех процессорах происходит обмен данными со сдвигом (n-й процессор передает данные процессору с номером n+1). Далее выполняется блок b2 и происходит загрузка ускорителей данными. После выполнения векторных операций на ускорителе происходит обратная передача данных в память узла. Затем выполняется блок операций b3, после чего данные собираются процессором p1 и выполняется финальный блок b4.

Время выполнения блока зависит также от загруженности других ядер и объема памяти, используемой блоком. При вычислении времени выполнения будем учитывать коэффициент CR, определяющий замедление работы с памятью при ее одновременном использовании несколькими ядрами и зависящий от конкретной вычислительной системы [2].

В общем случае время передачи данных между двумя блоками можно оценить по формуле

T=T0 +N×Tb,                                                            (1)

где T0 – латентность; Tb – время передачи байта; N – количество передаваемых байт.

Рассмотрим три возможных случая: передача данных между ядрами, между процессором и ускорителем, между вычислительными узлами.

Передача данных между ядрами. В данном случае возможно использование двух моделей – MPI и OpenMP.

В модели MPI используется разделение данных между ядрами, и общих данных у фрагментов программы на разных ядрах нет. Вычисления на разных ядрах организуются как отдельные задачи. При использовании модели MPI время передачи Ts можно оценивать формулой (1).

В модели OpenMP все ядра работают над общей памятью. При этом часть данных может быть продублирована, часть защищена семафорами от одновременного использования. При использовании модели OpenMP время разблокировки семафора можно считать латентностью T=T0. При этом латентность может быть весьма большой из-за ожиданий разблокировки данных. Передача дублирующихся данных может быть оценена формулой (1).

Передача данных между процессором и ускорителем. В данном случае при инициализации программы на ускорителе требуется передача данных от процессора к ускорителю и при ее завершении обратно. Поэтому необходимо передавать все используемые и полученные данные, что составляет большой объем. Обозначим In(bi) множество входных данных, Out(bi) – множество выходных данных, которые используются далее в программе, Ng(x) – количество байт, занимаемое множеством x, Tbgk  – время передачи одного байта к/от ускорителю. Для автоматического определения этих множеств можно использовать, например, формулы из [3]. В настоящее время ускорители (такие как NVIDIA Tesla, Intel Phi, AMD FireStream) подключаются по PCI-шинам, и время передачи данных Tsigk можно оценивать формулой Tsigk=2*T0gk+(Ng(In(bi))+Ng(Out(bi)))*Tbgk в предположении, что все параметры передачи данных к ускорителю и обратно симметричны. Следует отметить, что эти значения времени относятся только к ускорителю, то есть фактически время выполнения на ускорителе k составляет Tbigk+Tsigk .

Передача данных между узлами. В большинстве случаев используется модель MPI, так как общих данных у разных узлов нет. Время передачи между такими узлами можно оценивать по формуле (1).

Рассмотрим некоторые типичные случаи обмена данными. Наиболее часто используются следующие типы обмена данными: обмен с «соседями» (например, между узлами многомерной решетки) и коллективные передачи (один ко всем, все к одному).

Передача данных между соседними узлами. При решении физических задач часто применяется метод геометрического разбиения областей [4]. При этом используются «теневые» грани – данные, дублирующиеся на соседних узлах многомерной решетки. После выполнения очередного шага граничные значения передаются соседям k-мерной решетки. При этом Ts=2*k(T0n+N*Tbn).

Коллективные операции. Данный вид операции широко применяется при организации вычислений. Он используется при рассылке данных от одного узла ко всем, при выполнении редукционных операций, во многих дискретных алгоритмах [5]. Если операция рассылки не организована аппаратно, она требует log(P) шагов, где P – количество вычислительных узлов. Таким образом, время передачи данных составит Ts=(T0n+Tbn×N) log(P).

Заметим, что приведенные выше оценки времени передачи составлены для неблокирующих сетей, то есть сетей, пропускная способность которых позволяет обеспечить независимую одновременную передачу данных. Когда передачи данных влияют друг на друга, можно использовать коэффициент замедления CL, определяемый аналогично коэффициенту CR [2].

Определение численных параметров

Для проведения оценок с помощью приведенной выше модели необходимо определить численные параметры программы и системы. Для определения численных параметров можно использовать следующие методы.

Профилирование задачи на вычислительной системе. Данный метод является самым точным, однако не всегда возможно получение полных данных из-за большого объема работы, так как необходимо иметь данные по работе каждого блока на каждом оборудовании, а также по всем передачам данных.

Моделирование выполнения программы на системе. Возможно использование автоматических средств, таких как BERT-77/Ratio. Для каждой вычислительной системы определяются базовые параметры (время выполнения операций, параметры коммуникационной сети). С учетом этих параметров делается оценка времени выполнения программы. Достоинствами этого метода являются большая точность и достаточно высокая оперативность получения решения, недостатками – меньшая точность предсказания и проблематичность учета оптимизации компиляторов.

Оценка с учетом модели программы и системы. Каждому компоненту вычислительных систем присваиваются условные метрики производительности. Оценка времени выполнения производится умножением сложности блока на метрику производительности. Данный метод имеет низкую точность и может применяться при предварительной оценке для сокращения количества вариантов оборудования для вычислительных систем.

Для получения данных при решении таких задач в МСЦ РАН составлены наборы тестов р (бенчмарок), включающие в себя моделирование нелинейного электронного транспорта, моделирование течения недорасширенной струи вязкого газа, расчет Эйлеровой модели атмосферы, моделирование теплового движения воды, расчет течений с тепловыми неоднородностями, расчет молекулярной динамики сложной биологической системы и другие. Была разработана тестовая программа LAPTEST, определяющая производительность ядер при выполнении операций с плавающей точкой, оперативной памяти при выполнении операций чтения-записи, коммуникационной среды.

Выбор оборудования по быстродействию и стоимости

Выбор оборудования по быстродействию. Одной из основных задач выбора вычислительной системы является задача определения компонентов системы для обеспечения максимального быстродействия при решении заранее определенных задач.

При выборе оборудования по быстродействию следует учитывать, что не любые комбинации процессорных модулей могут выпускать фирмы-вендоры. Поэтому существуют ограничения на конкретные модели узлов, такие как количество процессоров, ускорителей, объем и скорость памяти.

При данных ограничениях оптимизируется целевая функция , где Tsi – время передачи данных после блока i.

Данная функция представляет собой сумму значений времени выполнения всех программных блоков и обменов данными.

Выбор оборудования по стоимости. Другой задачей выбора вычислительной системы является задача определения компонентов системы для обеспечения минимальной стоимости системы при решении заранее определенных задач. Выбор оборудования по стоимости производится аналогично выбору по быстродействию и должен проводиться с учетом похожих краевых условий, кроме того, время выполнения каждой программы не должно превышать заданное. Данная задача усложняется еще и тем, что с высокой точностью аналитически задача решается только для небольших кластеров, детали которых продаются по фиксированной цене. В реальности стоимость оборудования является предметом торгов (в частности, определенных 94-ФЗ) и может меняться. Минимальная стоимость оборудования, как правило, является коммерческой тайной. Поэтому при решении данной задачи точность может оказаться недостаточной, и данный метод может продуктивно использоваться для предварительной оценки рынка. Хорошее решение можно получить в случае, когда одна из архитектур имеет явное преимущество для данной задачи.

Разновидностью данной задачи является выбор оборудования с максимальной производительностью при фиксированной стоимости.

Описанный метод использовался в МСЦ РАН при выборе архитектуры высокопроизводительных систем. Оптимизировалось быстродействие для набора бенчмарок. Для построения априорной оценки использовалась программа BERT77/RA­TIO. С помощью данного подхода была оптимизирована архитектура таких вычислительных систем, как МВС-10BM, МВС-6000IM, МВС-100К.

Литература

1.     Телегин П.Н., Шабанов Б.М. Связь моделей программирования и архитектуры параллельных вычислительных систем // Программные продукты и системы. 2007. № 2. C. 5–8.

2.     Шабанов Б.М., Телегин П.Н., Аладышев О.С. Особенности использования многоядерных процессоров // Програм- мные продукты и системы. 2008. № 1. C. 7–9.

3.     Melnikov V., Shabanov B., Telegin P. and Chernyaev A. Automatic Parallelization of Programs for MIMD Computers, in Modern Geometric Computing for Visualization. Tokyo, Springer-Verlag, 1992. С. 253–262.

4.     Mattson T.G., Sanders B.A., Massingill B.L. Patterns for Parallel Programming. Addison-Wesley Professional, 2004.

5.     Akl S.G. The Design and Analysis of Parallel Algorithms. Prentice Hall, 1989.