Настройка выполнения параллельных программ
| Телегин П.Н. (pnt@jscc.ru) - Межведомственный суперкомпьютерный центр РАН (ведущий научный сотрудник), Москва, Россия, кандидат технических наук | |
| Ключевые слова: декомпозиция програм- мы., схема программы, планирование, кластер, автоматическое распараллеливание, модель программы, настройка программ, эффективность выполнения программ, параллельная программа |
|
| Keywords: program decomposition, program scheme, planning, cluster, automatic parallelization, model of program, program tuning, programs efficiency, parallel program |
|
|
|
|
Быстродействие программы на вычислительных кластерах зависит от того, насколько удачно она распараллелена. Для распараллеливания программы необходимо определить, что и как в программе будет выполняться параллельно. Однако для эффективной работы программы на кластере этого недостаточно. Различные вычислительные системы имеют разные параметры, влияющие на выполнение программ, – скорость работы процессоров, памяти, сетевых соединений. Поэтому для результативной работы распараллеленной программы на кластерной вычислительной системе нужно определить схему выполнения программы и распределение работы между процессорами (ядрами), то есть провести настройку выполнения параллельной программы.
Декомпозиция программы В качестве основного элемента параллельной декомпозиции, над которым производятся действия, рассматривается псевдолинейный участок, являющийся последовательностью блоков (программных структур) [1]. В качестве блоков рассмотрим следующие: Op – простой оператор языка, в том числе содержащий вызовы подпрограмм; If – структура ветвления (if-then-else, case); Lp – цикл (явный или неявный); Sd – неструктурированный участок программы с одним входом и выходом. Цикл может содержать дополнительные выходы (такие, как leave). В случае, если дополнительный выход приходится не на конец цикла, цикл может рассматриваться либо как cложный заголовок блока If, либо как элемент блока Sd. Декомпозиция может быть выполнена вручную или с помощью анализатора программ, таких как BERT-77 [2] или Ratio. Рассмотрим пример анализа декомпозиции и выбора схемы загрузки для потоковой, динамической и статической моделей выполнения программ [3]. Представим псевдолинейный участок: op1 CALL S1(X)lp2 DO I=1, N CALL S2(Y(I)) ENDDOop3 CALL S3(Z) В данном примере подпрограммы не имеют побочного эффекта и псевдолинейный участок состоит из трех независимых блоков: op1, lp2 и op3. Цикл lp2 является параллельным. Время исполнения примем равным: op1 – 25 мс, lp2 – 100 мс, op3 – 35 мс. В потоковой или динамической схеме master/ worker (хозяин–слуга) master во время выполнения программы производит распределение работы между процессами worker (рис. 1). Обозначим m число частей, на которые разбит цикл lp2. В потоковой схеме для процессов хозяин и слуга используются разные коды программы, а в динамической – программная схема SPMD (одинаковый код программы для всех процессов). Для динамической схемы имеем следующую программу: IF(master) THEN ! «хозяин» n_parts = n_workers = m+2 ! вычисление количества параллельных частейDO i_part=1, n_workersreceive data from worker w ! получение данных от «слуги»load_worker(w, i_part) ! отправка «слуге» очередных данных ! данных или признака окончания ENDDOELSE work = .true. DOWHILE(work) отправка признака готовности получение очередного задания part goto (1, 2, 3, 4), part1 receive x from master call s1(x) ! op1send x to mastergoto 5 2 receive z from mastercall s3(z) ! op3send z to mastergoto 53 receive imin, imax, y(imin:imax) from masterDO i = imin, imax ! lp2 call s2(y(i))ENDDOsend y(imin:imax) to mastergoto 54 work = .false. ! завершение работы5 CONTINUEENDDOENDIF broadcast(x, y, z) ! рассылка данных При использовании четырех ядер и m=4 получим загрузку ядер, представленную на рисунке 2, как для потоковой, так и для динамической схемы. Разбиение цикла при m=10 представлено на рисунке 3.
Можно заметить, что в потоковой и динамической схемах память узлов используется неэффективно из-за значительного дублирования данных. Статическая модель основывается на распределении данных (в первую очередь массивов) между локальной памятью каждого узла. Как правило, при увеличении количества узлов объем памяти, требуемый узлом, уменьшается. Рассматриваемый псевдолинейный участок в предположении, что n делится нацело на 4, может быть представлен как программа в статической модели: real y(n/N_nodes) ... low = P*(n/N_nodes)+1if(current_node .eq. node1) then s1(x)else if(current_node .eq. node2) then s3(z)endifhigh = (P+1)*(n/N_nodes)do I = low, high call s2(y(I- P*(n/N_nodes)) enddo
Оценка времени выполнения Методы оценки времени работы. Для планирования вычислений требуется оценка времени выполнения передачи данных программным блоком. Оценка времени выполнения программных элементов является сложной задачей. Рассмотрим три способа оценки времени работы программных фрагментов: предсказание времени работы, результат профилирования, оценка пользователем. Предсказание времени работы. Время оценивается путем анализа программного кода. Основной проблемой данной оценки являются нечеткие и неполные данные. В системе Ratio определяется время выполнения инструкций для конкретной вычислительной системы, которое является основой в определении времени выполнения инструкций. При определении времени выполнения составных программных объектов для ветвлений присваиваются вероятности переходов, для циклов оценивается количество итераций. В тех случаях, когда количество итераций не может быть получено путем анализа заголовка цикла (например, значения параметров цикла вводятся из файла), используются размерности массивов, обрабатываемых в цикле. Эксперименты, проведенные с Ratio, показывают недостатки данного метода: – невозможность предсказать результат оптимизации произвольного компилятора для конкретной вычислительной системы, влияющий на время выполнения; проблема усугубляется тем, что в последовательной и параллельной программах оптимизация может проводиться по-разному; – в случаях косвенной оценки числа итераций цикла иногда наблюдается эффект усиления: если размерности массивов были выбраны программистом с запасом, то при глубоком вложении циклов ошибки оценки количества итераций увеличивались в геометрической прогрессии. Профилирование. В системе Ratio возможно генерирование текста со вставленным кодом профилирования. Чтобы время выполнения программы значительно не замедлялось, профилируются не отдельные инструкции, а объекты, на основании данных о которых принимается решение о выборе схемы параллельного выполнения, а также определяется количество итераций для каждого цикла. Основным недостатком данного метода является то, что для профилирования пользователь выполняет задачу существенно меньшего объема, чем требуется. Из-за этого могут меняться соотношения между частями программы и оценки эффективности. Оценка пользователем. Пользователь дает указания автоматической или автоматизированной системе о значениях ключевых переменных, количестве итераций циклов, а также о времени выполнения участков программы. Недостаток данного подхода в том, что от пользователя требуется знание программы и основ распараллеливания. Система в диалоге может указать, какие параметры требуются, но при этом от пользователя все равно может потребоваться изучение программы. Указание времени выполнения пользователем является интуитивно неясным, так как речь идет о выполнении на разных системах. Таким образом, каждый из перечисленных подходов имеет существенные недостатки. Для их сокращения система Ratio использует все три подхода. Время коммуникаций. Время передачи данных между процессорами кластера определяется двумя базовыми параметрами: латентностью и временем передачи единицы информации. Как можно заметить, в системах с распределенной памятью латентность при передаче данных соответствует нескольким тысячам операций. При типичной латентности Tlat»5 мкс время выполнения одной итерации Ti может составить порядка 1 нс. Таким образом, отношение латентности ко времени выполнения одной итерации R=Tlat/Ti» »5 000. Такое соотношение требует тщательного анализа программы для принятия решения о ее параллельном выполнении. Рассмотрим базовые коммуникации. Простая передача данных. Обозначим количество передаваемых данных D, а время передачи одного байта Tbyte. В этом случае время передачи Tsend может быть выражено простой формулой: Tsend=Tlat+Tbyte*D. Коллективные операции (рассылка и редукция) в большинстве программных реализаций требуют log(N) шагов, где N – количество узлов. На каждом шаге необходимо передавать D байт. Таким образом, время рассылки Tbroadcast выражается как Tbroadcast=Tsend*log(N)=(Tlat+Tbyte*D)* log(N). Планирование параллельных циклов. Для определения времени выполнения параллельного цикла нужно знать количество передаваемых данных, время выполнения итерации и параметры сети (латентность и время передачи байта). Заметим, что время выполнения итерации может зависеть, с одной стороны, от особенностей оптимизации компилятором, с другой – от эффектов кэш-памяти. В подобных случаях это может как снизить эффективность параллельной программы, так и увеличить, приведя к сверхлинейному ускорению. Рассмотрим планирование цикла DO на N ядер в различных моделях выполнения [4]. Для итерации цикла используем оценки среднего и минимального времени выполнения. Желательно также иметь приемлемую оценку максимального времени, что не всегда возможно. Введем обозначения: Ti – среднее время итерации цикла; Tm – минимальное время итерации цикла; L – количество итераций цикла; Dc – количество одинаковых для всех процессов данных, подлежащих рассылке; Dv – количество различных для процессов данных, подлежащих рассылке. Рассмотрим планирование следующего цикла для разных схем выполнения: real*4 a(100), b(100) … do i = 1, 100 do j = 1, 50 a(i) = a(i) + b(j) enddo enddo Примем такие значения параметров: L=100, Dc=200 (b(1:50)), Dv=4 (a(i)). Потоковая схема. В этой схеме данные пересылаются от хозяина к слуге перед выполнением части цикла, а после выполнения отсылаются от слуги к хозяину. Данные, требуемые частями цикла, обозначим IN; вычисляемые частями цикла – OUT; вычисляемые редукционными операциями – REDUC. Пусть Niter – количество итераций в части цикла; Nin – количество байтов IN: Nin=Dc+Niter*Dv, где Niter – количество итераций. Заметим, что данные, требуемые для организации цикла, добавляются к Dc. Аналогичные формулы верны для данных OUT и REDUC, в частности: Nout=Rc+Npart* Rl+Rv, где Npart – количество частей, на которые разбит цикл; Rc – объем данных, вычисляемых слугой, не зависящий от числа итераций (редукции); Rl – объем данных, вычисляемых слугой, зависящий от числа итераций; Rv – объем данных, вычисляемых слугой, определяемый на последней итерации. Рассмотрим два случая. 1-й случай: Nin>Nout, то есть объем входных данных (множества IN) превышает объем выходных данных (множества OUT). На рисунке 5 приведена временная диаграмма для четырех процессов «слуга». Показаны прием исходных данных (включая ожидание), выполнение и передача результатов. Как можно заметить, на критическом пути находится передача данных множества IN. Для OUT на критическом пути находится только последняя порция данных. В данном случае время выполнения цикла Tц=Nw*Tsend(Nin)+Tsend(Nout)+Torg+L/Nw*Ti в предположении, что количество слуг не превышает количество ядер, где Nw – количество слуг; Torg – время организации цикла; Tsend(Nin)=Tlat+ +Tbyte*(Dc+L/Nw*Dv), где Tlat – латентность сети, Tbyte – время передачи одного байта; Torg=Tcorg+Nw*Tvorg, где Tcorg – постоянная часть; Tvorg – переменная часть. Таким образом,
Эта функция достигает минимума при Заметим, что время редукционных операций можно учитывать при Tvorg. 2-й случай: Эта ситуация противоположна предыдущей. Время выполнения цикла Tц=Nw*Tsend (Nout)+ +Tsend (Nin)+Torg+L/Nw*Ti. Критерий минимизации аналогичен, при этом меняются множества IN и OUT. В динамической схеме данные множества IN не передаются, а данные множества OUT сначала принимаются хозяином после завершения части работы слуги, а затем рассылаются всем процессам. В этом случае время выполнения цикла
С учетом времени рассылки данных
Данная функция достигает минимума при
Тестирование. Описанные методы оценки производительности реализованы в системе автоматизированного распараллеливания Ratio. Приведем результаты сравнения предсказанного и реального ускорений программы интегрирования. Параллельная программа была построена с помощью системы автоматизированного распараллеливания Ratio. При анализе системой Ratio выбрана динамическая модель. Результаты измерений выполнения программы на вычислительной системе МВС-100К в МСЦ РАН приведены в таблице. Точность оценки ускорения представляется достаточной для принятия решения о планировании циклов с учетом факторов, трудно поддающихся априорному анализу, таких как распределение кэш-памяти. Результаты прогонов программы на МВС-100К
Подытоживая, отметим, что в статье предложен метод выбора схемы параллельной программы на основе автоматического предсказания времени выполнения программных фрагментов. Данный метод реализован в системе автоматизированного распараллеливания Ratio, проведена оценка его эффективности. литература 1. Melnikov V., Shabanov B., Telegin P. and Chernjaev A. Automatic Parallelization of Programs for MIMD Computers. Springer-Verlag, Tokyo, 1992. 2. Telegin P. and Eadline D. An Easier Way. Clusteworld, 2004, Vol. 2, November, pp. 42–45. 3. Telegin P. Scheduling Paralel Programs. Clusterworld, 2004, September, pp. 40–43. 4. Шабанов Б.М., Телегин П.Н., Телегина Е.В. Влияние архитектуры на модели программирования параллельных вычислительных систем // Изв. вузов: Электроника. 2011. № 2 (88). С. 60–65. 5. Суперкомпьютер МВС-100K. URL: http://www.jscc.ru/ hard/mvs100k.shtml (дата обращения: 24.08.2012). |
http://swsys.ru/index.php?id=3304&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Кластеры распределенной системы тренажерно-моделирующего комплекса в задаче агрегации фракталов
- Информационная система аналитического сценария формирования долга региона
- Использование параллельной обработки данных для оптимизации работы программного обеспечения
- Метод планирования инновационной деятельности
- Автоматизированная система планирования полета Российского сегмента международной космической станции

 Для такой настройки используются параллельная декомпозиция программы, оценки времени выполнения программных фрагментов на заданном оборудовании и параметры коммуникационной сети.
Для такой настройки используются параллельная декомпозиция программы, оценки времени выполнения программных фрагментов на заданном оборудовании и параметры коммуникационной сети.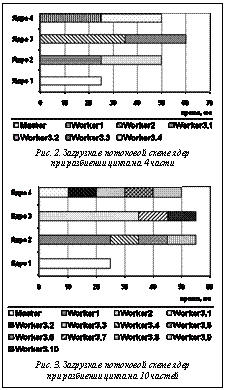 Таким образом, путем мелкого разбиения цикла можно добиться лучшей загрузки, в данном примере время сократилось с 60 до 55 мс. Однако в реальности время организации работы параллельных частей и передачи данных ограничивает разбиение.
Таким образом, путем мелкого разбиения цикла можно добиться лучшей загрузки, в данном примере время сократилось с 60 до 55 мс. Однако в реальности время организации работы параллельных частей и передачи данных ограничивает разбиение.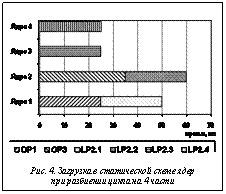 Диаграмма загрузки при разбиении памяти на 4 ядра представлена на рисунке 4.
Диаграмма загрузки при разбиении памяти на 4 ядра представлена на рисунке 4.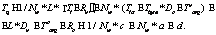

 Nout>Nin, то есть объем выходных данных превышает объем входных данных.
Nout>Nin, то есть объем выходных данных превышает объем входных данных.
 имеем:
имеем:

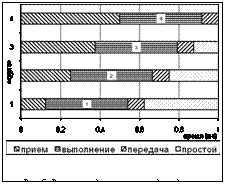 Планирование статической схемы похоже на планирование динамической. Главное отличие состоит в том, что коэффициенты a, b, c, d не вычисляются для конкретного цикла, а суммируются для множества циклов, часто для всех параллельных циклов в программе.
Планирование статической схемы похоже на планирование динамической. Главное отличие состоит в том, что коэффициенты a, b, c, d не вычисляются для конкретного цикла, а суммируются для множества циклов, часто для всех параллельных циклов в программе.