Системная динамика в задачах мониторинга массовой вакцинации населения
| Лапшина С.Ю. (lapshina@jscc.ru) - Межведомственный суперкомпьютерный центр РАН – филиал ФНЦ НИИСИ РАН (начальник научно-организационного отдела), Москва, Россия | |
| Ключевые слова: верификация модели., блоки, кон- цепты, ресурсы модели, агрегатная модель, системная динамика, имитационное моделирование |
|
| Keywords: model's verification, building blocks, concepts, model's resources, aggregate model, system dynamics, simulation |
|
|
|
|
Массовые эпидемии и пандемии наносят непоправимый ущерб населению всего мира. На случай ожидаемых пандемий во многих странах реализуются соответствующие программы опережающих научных исследований, в том числе и компьютерное моделирование мероприятий по распространению болезней и противодействию им. В данной статье приведено описание агрегатной модели мониторинга мероприятий по вакцинации населения на основе методов системной динамики, проведенных имитационных экспериментов и верификации модели. Модель разрабатывалась с использованием современных концепций взаимодействующих фондовых потоков (ВФП) и визуального программирования в рамках возможностей одного из популярных пакетов имитационного моделирования IThink 9.0.2 [1–3]. В разработке модели использовались материалы, связанные с мероприятиями по преодолению последствий вспышки и распространения эпидемии гриппа A/H1N1 в Москве в 2009–2010 гг. [4, 5]. Базовые концепты модели Следуя концепциям ВФП, на первоначальном этапе прототипирования выделяются следующие агрегатные сущности (ресурсы) модели, текущее состояние которых в динамике характеризует состояние модельной ситуации в целом: НЕВАКЦИНИРОВАННЫЕ, ВАКЦИНИРОВАННЫЕ, УСПЕШНО_ВАКЦИНИРОВАННЫЕ, ИНФИЦИРОВАННЫЕ, ЗАБОЛЕВШИЕ, ПЕРЕБОЛЕВШИЕ, ПРИОБРЕТШИЕ_ИММУНИТЕТ, УМЕРШИЕ. Ресурсы (как первичные базовые концепты) сосредоточены во взаимодействующих концептуальных блоках ВАКЦИНАЦИЯ И ВСПЫШКА ЭПИДЕМИИ, ИНФИЦИРОВАНИЕ и ПРОТЕКАНИЕ БОЛЕЗНИ (рис. 1). Поведение модели рассматривалось в контексте правдоподобных предположений: · население_по_переписи – 10 527 000; · коэффициент_рождаемости – 12,4; · миграционный_прирост – 31 368; · коэффициент_смертности – 14,2; · охват_вакцинацией – 0,24; · неэффективность_вакцины – 0,2; · способность_приобрести_иммунитет – 0,87; · количество_контактов_в_день – 4; · инкубационный_период – 2 дня; · t_выздоровления – 6 дней; · коэффициент_смертности_от_последствий_эпидемии – 0,2; · длительность_иммунитета_после_болезни – 365 дней; · длительность_периода_вакцинации – 91 день; · длительность_иммунитета_от_вакцины – 91 день. Первые пять относительно устойчивых факторов отображают наперед заданные статистические характеристики модели. Остальные используются как параметры предполагаемых имитационных экспериментов. Проектирование концептуальных блоков модели
Ресурс НЕВАКЦИНИРОВАННЫЕ пополняется потоками могут_заболеть, завершение_иммунитета_от_вакцины, вакцинация, неприобретение_ иммунитета и завершение_иммунитета_после_ болезни. Исчерпывается ресурс двунаправленным потоком вакцинация, а также потоками заражение_невакцинированных и умирание_невакцинированных_не_от_последствия_эпидемии. Поток умирание_невакцинированных_не_от_ последствия_эпидемии зависит от значения параметра коэффициент_смертности и от текущего значения ресурса НЕВАКЦИНИРОВАННЫЕ. Темп пополнения ресурса НЕВАКЦИНИРОВАННЫЕ потоком могут_заболеть определяется текущим значением переменных мигрировавшие и родившиеся. Значение переменной родившиеся зависит от значения параметра коэффициент_ рождаемости (12,4) и текущего значения переменной население, которое в динамике (рис. 3) будет складываться из содержимого ресурсов НЕВАКЦИНИРОВАННЫЕ, ВАКЦИНИРОВАННЫЕ, ИНФИЦИРОВАННЫЕ, УСПЕШНО_ВАКЦИНИРОВАННЫЕ, ЗАБОЛЕВШИЕ, ПЕРЕБОЛЕВШИЕ, ПРИОБРЕТШИЕ_ИММУНИТЕТ. Помимо прироста значения переменной родившиеся, в модели учитывается также прирост значения переменной мигрировавшие, зависящего от данных переменной население, описанной выше, и коэффициента_миграции, который, в свою очередь, зависит от значения параметра миграционный_прирост (31 368).
При неуспешной вакцинации (сработал, к примеру, фактор неэффективности вакцины) идет возврат к пополнению ресурса НЕВАКЦИНИРОВАННЫЕ, что отражено в модели двойным (бинаправленным) потоком вакцинация. Модельные единицы из ресурса ВАКЦИНИРОВАННЫЕ, пройдя успешную вакцинацию, попадают в ресурс УСПЕШНО_ВАКЦИНИРОВАННЫЕ либо происходит умирание вакцинированных не от действия вакцины (зависящее от количества вакцинированных и значения статистической константы коэффициент_смертности). Ресурс УСПЕШНО_ВАКЦИНИРОВАННЫЕ – это накопитель типа конвейер, исчерпывание которого осуществляется потоком убывание_успешно_вакцинированных_не_от_действия_вакцины, зависящим от значения статистической константы коэффициент_смертности (14,0) и параметра длительность_иммунитета_от_вакцины (по данным СМИ и Управления Роспотребнадзора –150 дней). От значения этого параметра зависит также и интенсивность потока завершение_иммунитета_ от_вакцины. В соответствии с интенсивностью данные из конвейера УСПЕШНО_ВАКЦИНИРОВАННЫЕ возвращаются в ресурс НЕВАКЦИНИРОВАННЫЕ.
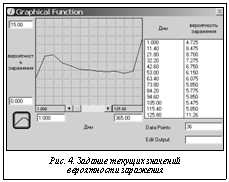
Помимо этого, базируясь на информации того же Управления Роспотребнадзора по городу Москве о заболеваемости ОРВИ и гриппом, был построен график зависимости вероятности заражения (рис. 4) от конкретной недели моделируемого периода (диктуемой, очевидно, временем года, погодными условиями и т.д.). Было также сделано предположение, что количество зараженных людей, являющееся спусковым механизмом начала эпидемии, равно 5 000. В блоке ИНФИЦИРОВАНИЕ (рис. 5) отображена динамика процессов периода инфицирования. Изначально объем ресурса ИНФИЦИРОВАННЫЕ равен 0. Его пополнение происходит двумя потоками из блока ВАКЦИНАЦИЯ И ВСПЫШКА ЭПИДЕМИИ: начало_эпидемии и заражение_невакцинированных. В этот ресурс соответственно попадают либо те, для кого вакцинация была неуспешна и они заболели, либо те, кто не проходил вакцинацию вообще и тоже заболел. Принимается во внимание, что может активироваться процесс умирание_инфицированных_не_от_последствий_эпидемии, который зависит от значения константы коэффициент_смертности и текущего значения параметра инкубационный_период. Инкубационный_период – это отрезок времени от момента попадания микробного агента в организм до проявления симптомов болезни (латентный период болезни). После завершения инкубационного периода проявляются симптомы болезни, и потенциальный пациент заболевает. Активность блока ПРОТЕКАНИЕ БОЛЕЗНИ (рис. 6) проявляет себя через исчерпывание потоком проявление_симптомов содержимого ресурса ИНФИЦИРОВАНИЕ и пополнение содержимого ресурса ЗАБОЛЕВШИЕ. Далее, подобно дисциплине пополнения и исчерпывания ресурсов в блоках ВАКЦИНАЦИЯ И ВСПЫШКА ЭПИДЕМИИ и ИНФИЦИРОВАНИЕ, пополняются и исчерпываются ресурсы ЗАБОЛЕВШИЕ, ПЕРЕБОЛЕВШИЕ и ПРИОБРЕТШИЕ_ИММУНИТЕТ в блоке ПРОТЕКАНИЕ БОЛЕЗНИ, а также лишь пополняется ресурс УМЕРШИЕ. Заметим, что исчерпывание ресурса ПЕРЕБОЛЕВШИЕ от последствий эпидемии зависит от значения параметра коэффициент_смертности_от_ последствий_эпидемии (для гриппа A/H1N1 – 0,2), который по сути и отображает интегрированные предположения о последствиях развития конкретного инфекционного заболевания в условиях эффективности мероприятий, диктуемых значениями наперед заданного набора входных параметров. Отображается также и убывание переболевших не от последствий эпидемии, которое зависит от показателя-константы коэффициент_смертности. Здесь используется совокупный коэффициент смертности, равный разности между статистическим коэффициентом смертности по России – 14,2 (количество умерших на 1 000 человек) и смертностью от последствий эпидемии. Смертность от последствий эпидемии предполагается равной 0,2 (учитываются лишь заболевшие). Также в показателе коэффициент_смертности нужно учесть ситуацию с умершими не от последствий эпидемии, то есть незаболевшими. Поэтому в разности используется значение 0,2. Тогда полученный коэффициент смертности 14,2–0,2=14,0.
Известно, что не все люди способны приобретать иммунитет. Такая способность принимается равной 87 %. Наконец, ПЕРЕБОЛЕВШИЕ, которые не приобрели иммунитет, становятся снова НЕВАКЦИНИРОВАННЫМИ, что отображается интенсивностью потока неприобретение_иммунитета. Этот процесс опять же зависит от значения константы способность_приобрести_иммунитет. Выясним, какие процессы могут происходить с ПРИОБРЕТШИМИ_ИММУНИТЕТ. Модель предлагает два пути развития проблемной ситуации. 1. Происходит их убывание_не_от_последствий_эпидемии, которое зависит от констант коэффициент_смертности и длительность_иммунитета_после_болезни. Здесь учитывается значение фактора врожденного иммунитета (наследственно обусловленного свойства), присущего данному виду. Предполагается, что действие иммунитета распространяется на весь моделируемый период (365 дней). 2. ПРИОБРЕТШИЕ_ИММУНИТЕТ вновь становятся НЕВАКЦИНИРОВАННЫМИ. Для получения более точных результатов и исследования болезни по данным Управления Роспотребнадзора по Москве о заболеваемости ОРВИ и гриппом (именно эта эпидемия рассматривалась в качестве основы модели) в модель были включены счетчики заболевших за неделю и больных предыдущего дня. Конструирование и локальная отладка stock and flow представлений блоков ВАКЦИНАЦИЯ И ВСПЫШКА ЭПИДЕМИИ, ИНФИЦИРОВАНИЕ и ПРОТЕКАНИЕ БОЛЕЗНИ позволили сформировать интегрированную поведенческую схему имитационного прототипа агрегатной модели. Верификация модели На основе разработанного в среде IThink 9.0.2 действующего прототипа была проведена серия имитационных экспериментов для верификации модели, которые подтверждили достоверность и объективность полученных результатов. Верификации производились при изменении фактора неэффективности вакцины из-за возможного открытия более эффективных вакцин или использования менее эффективных и параметров охвата вакцинацией, способности приобрести иммунитет, количества ежедневных контактов, длительности инкубационного периода, времени выздоровления, предполагаемой смертности от последствий эпидемии, а также параметра длительности сохранения иммунитета. Визуализация и анализ полученных результатов Сеансы имитации продемонстрировали, что при изначально выбранных значениях параметров пик заболеваемости гриппом A/H1N1 в Москве пришелся на 62–63-й день модельного времени развития эпидемии. Выяснилось, что до тех пор, пока не закончится период вакцинации (91–92-й день), количество невакцинированных уменьшается, а количество успешно вакцинированных соответственно растет. После окончания вакцинации и до конца сохранения иммунитета от действия вакцины количество невакцинированных продолжает уменьшаться. И в этом же периоде модельного времени количество успешно вакцинированных остается примерно на одном уровне (если точнее, незначительно уменьшается примерно на 26–27 тысяч в связи со смертностью населения как от последствий эпидемии, так и по другим причинам). Однако после окончания сохранения иммунитета от действия вакцины (через 150 дней) из-за прекращения действия прививки количество невакцинированных начинает увеличиваться, а количество успешно вакцинированных падает до нуля. Подобная картина наблюдается вплоть до 243-го дня (150 дней + длительность вакцинации) развития эпидемии. До конца моделируемого периода количество невакцинированных снова увеличивается, что связано с такими факторами, как рождаемость и миграция при низкой смертности. Тем не менее количество успешно вакцинированных остается на уровне нуля до самого конца моделируемого периода. Это происходит потому, что в течение летних месяцев вакцинируются редко и эпидемия естественным образом затухает. Кривые изменения числа переболевших, инфицированных и больных связаны с вероятностями заражения, соответствующими данным по еженедельному количеству заболевших. На основании изложенного можно сделать следующие выводы. По мнению автора, прототипы модели достаточно универсальны, то есть при задании значений определенных параметров можно прогнозировать результаты вакцинации населения практически для любой эпидемии в рамках каких-либо региона и карантинной зоны. Представляет также интерес возможность адаптации предложенной модели с целью прогнозирования результатов распространения опасных и вредоносных излучений (таких как электромагнитные, ионизированные, радиоактивные и т.д.), решения задач противодействия распространению компьютерных вирусов и т.п. Более того, модельные прототипы могут найти свое применение в решении широкомасштабных задач оценки и борьбы с распространением вредоносных микроорганизмов в геоэкологических системах. Действительно, экологическое равновесие в геоэкологических системах существенно зависит от характера их распространения. По сути мир сегодня оказался в положении, когда старые и новые инфекционные заболевания имеют высокий потенциал к бесконтрольному распространению с беспрецедентно высокой скоростью. Урбанизация, нарастающее ухудшение социально-экологических и санитарно-гигиенических условий жизни сотен миллионов людей в развивающихся и развитых странах мира, возрастающие миграционные потоки и процессы глобализации экономики способствуют быстрому распространению инфекционных заболеваний. Как это ни парадоксально, но сегодня реальная угроза начинает порождаться успехами высоких биотехнологий – генной инженерии и молекулярной биологии. Действительно, модифицированные микроорганизмы могут стать первопричиной возникновения массовых эпидемий и пандемий, например, в результате неконтролируемого выхода их из научных лабораторий и промышленных предприятий промышленно-развитых стран мира в результате техногенных аварий или природных катастроф. Очевидно, что эти новые аспекты современной эпидемиологии особо опасных инфекций еще предстоит глубоко изучать и анализировать, в том числе и с помощью методов математического и компьютерного моделирования. Литература 1. Вопросы системной динамики. URL: www.iseesystems.com (дата обращения: 8.09.2012). 2. Шебеко Ю.А. Введение в практику имитационного моделирования и ситуационного анализа стратегических инициатив: учеб. пособие. М., 2010. 3. Казаков С.А., Шебеко Ю.А. Введение в практику имитационного моделирования и анализа поведения сложных процессов и систем. M.: МИЭТ, 2006. 4. Грипп: вопросы лечения и профилактики гриппа. URL: http://www.gripp.ru/default.aspx (дата обращения: 8.09.2012). 5. Грипп. Вакцинация. URL: http://www.privivki.net/index.php?option=com_content&view=article&id=9&Itemid=13 (дата обращения: 8.09.2012). |
http://swsys.ru/index.php?id=3306&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Реализация субъективных методов вероятностной оценки адекватности тренажеров на основе комплекса программ с привлечением экспертов и анкетированием обучаемых
- Имитационная модель системы пакетирования суперкомпьютерных заданий на базе симулятора Alea
- Программный генератор трафика пользователей ресурса виртуальных лабораторий
- Программный комплекс автоматизации концептуального синтеза системно-динамических моделей
- Автоматизированный сценарий тренировки в тактическом тренажере


 По текущему объему ресурса НЕВАКЦИНИРОВАННЫЕ блока ВАКЦИНАЦИЯ И ВСПЫШКА ЭПИДЕМИИ (рис. 2) можно судить о том, сколько потенциальных клиентов в текущий момент времени считаются невакцинированными. Первичное содержимое ресурса НЕВАКЦИНИРОВАННЫЕ в начале моделируемого периода (365 дней) определяется значением константы население_по_переписи, которая для данных модельных представлений приравнивается к 10 572 000 человек.
По текущему объему ресурса НЕВАКЦИНИРОВАННЫЕ блока ВАКЦИНАЦИЯ И ВСПЫШКА ЭПИДЕМИИ (рис. 2) можно судить о том, сколько потенциальных клиентов в текущий момент времени считаются невакцинированными. Первичное содержимое ресурса НЕВАКЦИНИРОВАННЫЕ в начале моделируемого периода (365 дней) определяется значением константы население_по_переписи, которая для данных модельных представлений приравнивается к 10 572 000 человек.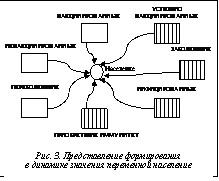
 Пополнение ресурса ВАКЦИНИРОВАННЫЕ идет за счет исчерпывания потоком вакцинация ресурса НЕВАКЦИНИРОВАННЫЕ под воздействием ряда факторов, таких как дневной_охват_вакцинацией, длительность_периода_вакцинации, текущий_день_ моделируемого_периода, параметром неэффективность_вакцины и содержимым ресурса ВАКЦИНИРОВАННЫЕ.
Пополнение ресурса ВАКЦИНИРОВАННЫЕ идет за счет исчерпывания потоком вакцинация ресурса НЕВАКЦИНИРОВАННЫЕ под воздействием ряда факторов, таких как дневной_охват_вакцинацией, длительность_периода_вакцинации, текущий_день_ моделируемого_периода, параметром неэффективность_вакцины и содержимым ресурса ВАКЦИНИРОВАННЫЕ. Рассмотрим процесс заражение_невакцинированных в предположении, что количество контактов больного человека равно 4. Акт заражения невакцинированных связан а) со значением па- раметра количество_контактов_в_день, б) вероятностью того, что больной встретится с невакцинированным, в) текущим содержимым ресурса ЗАБОЛЕВШИЕ, г) процентом невакцинированных (определяемым текущим значением выражения больные*процент_невакцинированных/100). Процент невакцинированных, в свою очередь, зависит от текущего значения переменной население и текущего значения содержимого ресурса НЕВАКЦИНИРОВАННЫЕ.
Рассмотрим процесс заражение_невакцинированных в предположении, что количество контактов больного человека равно 4. Акт заражения невакцинированных связан а) со значением па- раметра количество_контактов_в_день, б) вероятностью того, что больной встретится с невакцинированным, в) текущим содержимым ресурса ЗАБОЛЕВШИЕ, г) процентом невакцинированных (определяемым текущим значением выражения больные*процент_невакцинированных/100). Процент невакцинированных, в свою очередь, зависит от текущего значения переменной население и текущего значения содержимого ресурса НЕВАКЦИНИРОВАННЫЕ. ПЕРЕБОЛЕВШИЕ могут приобрести так называемый искусственный_активный_иммунитет, формируемый вакцинацией. Пациенту прививаются ослабленные или убитые вирусы. В результате развивается первичный иммунный ответ организма, а при попадании нормального неослабленного возбудителя заболевания обеспечивается вторичный ответ, ведущий к легкому течению болезни и быстрому обезвреживанию антигена. Методами генной инженерии создаются безвредные вакцины, не имеющие в своем составе поражающего фактора (ДНК или РНК вирусов или бактерий), но содержащие их поверхностные белки, на воздействие которых развивается иммунный ответ. Предполагается, что приобретенный (индивидуальный) иммунитет возникает после перенесения потенциальным клиентом какого-то заболевания, то есть у каждого индивида он свой.
ПЕРЕБОЛЕВШИЕ могут приобрести так называемый искусственный_активный_иммунитет, формируемый вакцинацией. Пациенту прививаются ослабленные или убитые вирусы. В результате развивается первичный иммунный ответ организма, а при попадании нормального неослабленного возбудителя заболевания обеспечивается вторичный ответ, ведущий к легкому течению болезни и быстрому обезвреживанию антигена. Методами генной инженерии создаются безвредные вакцины, не имеющие в своем составе поражающего фактора (ДНК или РНК вирусов или бактерий), но содержащие их поверхностные белки, на воздействие которых развивается иммунный ответ. Предполагается, что приобретенный (индивидуальный) иммунитет возникает после перенесения потенциальным клиентом какого-то заболевания, то есть у каждого индивида он свой.