Моделирование отражений окружающей среды для виртуальных объектов в реальном режиме времени
| Мальцев А.В. (avmaltcev@mail.ru) - НИИСИ РАН, г. Москва, г. Москва, Россия, кандидат физико-математических наук, Михайлюк М.В. (mix@niisi.ras.ru) - НИИСИ РАН, г. Москва, Москва, Россия, доктор физико-математических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Одним из способов повышения реалистичности виртуальных объектов является моделирование и реализация отражений от их поверхностей окружающей обстановки. Существуют несколько методов имитации таких отражений, среди которых большой популярностью пользуются сферические и кубические карты (текстуры) отражения окружающей среды, входящие в группу карт отражений (reflection maps). Реалистичность отражений, полученных с помощью таких карт, достигается особенным, отличным от обычного процессом наложения карты среды на поверхность объекта. Так, при перемещении в сцене объекта, использующего карту отражения, на его поверхности наблюдается изменение рисунка, в отличие от случая с обычной текстурой, которая остается жестко связанной с объектом при его движении. Сферические и кубические карты окружающей среды поддерживаются во многих системах трехмерного моделирования, в том числе в 3D-Studio Max. Так как сферические карты среды из-за своей зависимости от положения наблюдателя применимы в основном только для статичных виртуальных сцен, то в данной работе рассматривается реализация в реальном режиме времени кубических карт окружающей среды (cube environment mapping), дающих хороший результат как в статичных, так и в динамичных сценах. Кубические карты окружающей среды Кубическая карта состоит из шести планарных карт среды, образующих грани куба, в центре которого располагается отражающий объект. Каждая карта является проекцией окружающей обстановки из центра куба на соответствующую его грань. При расчете отражения на объекте для каждой видимой точки на его поверхности проводится луч из центра объекта до пересечения с кубом, и цвет точки пересечения берется в качестве цвета отражения окружающей среды. При фиксированной кубической карте объект и камера могут перемещаться, и при этом отражения на объекте будут также меняться. Сами карты окружающей среды могут быть статичными и динамичными, то есть могут быть созданы заранее и создаваться на лету в процессе изменения в сцене самой окружающей среды. В системе 3D-Studio Max отражение окружающей среды с помощью кубической карты можно реализовать тремя способами: 1) используя заранее подготовленную кубическую карту; 2) генерируя для каждого отражающего объекта кубическую карту отражения окружающей среды только в первом кадре; 3) генерируя для каждого отражающего объекта кубическую карту отражения окружающей среды в каждом N-м кадре.
Подставляя в него значения Cosa=(N,-U)=-(N,U) и ||U||=1, получаем отраженный вектор RVCS = R = U – 2(N, U)N. (1) Рассмотрим, как по вектору RVCS вычислить текстурные координаты в кубической карте. В системе 3D-Studio Max кубическая карта среды задается в системе координат OWCS, центр которой совпадает с центром объекта, а оси направлены так же, как в мировой системе (WCS). Так как видовая матрица MV текущей виртуальной камеры осуществляет преобразование из видовой в мировую систему, то вектор RVCS в системе OWCS будет иметь координаты RОWCS = (MV)-1 · RVCS. (2)
При реализации отражений с помощью графической библиотеки OpenGL следует иметь в виду, что в ней кубическая текстурная карта имеет свою систему координат (Cube Map Coordinate System, CMCS), повернутую относительно системы ОWCS вокруг оси X на 90° (рис. 2). Матрица поворота имеет вид
а вектор R в системе CMCS будет иметь координаты RCMCS = Mrot · ROWCS = Mrot · (MV)-1 · RVCS . (3) Умножение вектора ROWCS=(x,y,z) на матрицу Mrot дает вектор (x,-z,y), поэтому в целях оптимизации возможна замена умножения на матрицу Mrot перестановкой (с учетом знаков) координат y и z вектора ROWCS. Ориентация текстурных карт на гранях куба также отличается в системах OpenGL и 3DS MAX. Так, например, из рисунка 2 видно, что передняя грань куба (FRONT) расположенная в системе ОWCS по направлению -Y, должна соответствовать передней грани в системе CMCS по направлению -Z, а следовательно, иметь стандартное имя GL_TEXTURE_CUBE_MAP_NEGATIVE_Z_ARB. В таблице приведено полное соответствие имен и ориентаций граней кубической карты в системах ОWCS и CMCS. Таблица
По вектору RCMCS, найденному из равенств (1) и (3), необходимо определить, какую грань куба следует взять и как на ней вычислить соответствующие текстурные координаты. В качестве текстурных координат для кубической карты среды выступают координаты x, y и z вектора RCMCS. Они задают направление луча, выходящего из начала координат и пересекающего одну из граней единичного текстурного куба. Пересекаемая грань определяется текстурной координатой, имеющей наибольшее по модулю значение, и знаком этой координаты. Например, если |x|>|y|, |x|>|z| и x>0, то выбирается правая грань текстурного куба (GL_TEXTURE_CUBE_MAP_POSITIVE_X_ARB). Координаты s и t выбранной двухмерной текстурной карты вычисляются по оставшимся координатам y и z, используя формулы
В случае визуализации без использования шейдеров можно не подсчитывать текстурные координаты для кубической карты среды самостоятельно, а воспользоваться стандартной функцией автоматической генерации текстурных координат glTexGeni, подставив в качестве параметра генерации GL_REFLECTION_MAP_ARB. При этом координаты будут рассчитываться на основе вектора R, но представленного в видовой системе координат. Чтобы расчет производился в системе CMCS, требуется выбрать текстурную матрицу с помощью glMatrixMode(GL_TEXTURE) и загрузить в нее (glLoadMatrixf) матрицу, равную Mrot · (MV)-1 (см. формулу (3)). На рисунке 3 показан пример реализации отражения на основе кубической карты окружающей среды. Второй способ реализуется аналогично первому, за исключением того, что вместо заранее подготовленной кубической карты среды, взятой из графических файлов, используется сгенерированная в первом кадре кубическая карта. Процесс генерации такой карты для объекта состоит из следующих пунктов: 1) рендеринг сцены по шести взаимно-перпендикулярным направлениям из центра объекта с получением, соответственно, шести изображений; 2) создание кубической карты из полученных шести изображений.
Расположим камеру в точке, совпадающей с началом локальной системы координат OCS объекта. Для того чтобы видовая система координат камеры совпадала с системой ОWCS, необходимо задать видовую матрицу следующим образом: MV = где (m03, m13, m23, 1) – последний столбец модельной матрицы MМ объекта, то есть столбец, отвечающий за перенос. Действительно, единичная подматрица матрицы MV обеспечивает то, что направления осей видовой системы будут совпадать с направлениями осей мировой системы координат, а последний столбец – то, что начало координат видовой системы будет совпадать с началом локальной системы координат объекта. Для формирования правильной карты среды в данном случае начало локальной системы координат должно находиться в геометрическом центре объекта. При построении объекта сцены в системе моделирования 3D-Studio Max начало его локальной системы OCS в общем случае не совпадает с геометрическим центром. Однако с помощью специального параметра pivot систему OCS можно смещать относительно объекта. Поэтому при формировании сцены в 3D-Studio Max дизайнер должен для каждого отражающего объекта задать точку pivot в центре этого объекта. Так как направление взгляда камеры определяется осью –Z, то камера, заданная видовой матрицей MV, и является искомой. Матрицы для остальных камер можно получить из MV путем умножения слева на матрицу вращения в нужном направлении. После визуализации окружающей среды каждой из шести определенных выше камер получается шесть изображений, которые представляют стороны кубической карты окружения для рассматриваемого объекта. Применение этой карты полностью аналогично первому способу. Для генерации кубической карты и визуализации сцены в реальном времени целесообразно применение так называемого рендеринга в текстуру с использованием p-буфера. P-буфер – это пиксельный буфер, хранящийся непосредственно в видеопамяти, обладающий собственным размером и другими атрибутами и не связанный с основным буфером кадра. При этом содержимое p-буфера может быть использовано в качестве текстуры, а рендеринг в p-буфер аппаратно ускорен (см.: А.В. Боресков. Расширения OpenGL. СПб. 2005). Другими словами, отрисовав последовательно каждую из шести граней кубической карты в p-буфер, мы получим готовую кубическую карту, находящуюся в видеопамяти и пригодную для использования в качестве карты отражения окружающей среды. Данный метод позволяет избежать лишнего копирования данных из видеопамяти в оперативную память и обратно, которое требовалось бы в других реализациях, что заметно повышает скорость визуализации в реальном режиме времени и дает возможность увеличить качество отражений. Для подключения p-буфера на платформе Windows и получения возможности использования его в качестве текстуры необходимо инициализировать расширения OpenGL WGL_ARB_ pixel_ format, WGL_ARB_ pbuffer и WGL_ARB_render_ texture. Третий способ отличается от второго только тем, что через каждые N кадров необходимо повторять процедуру генерации кубической карты среды, а в остальных кадрах использовать кубическую карту, созданную при предыдущей генерации. Этот способ наиболее эффективен в виртуальных сценах, где объекты окружения находятся в динамике, а следовательно, отражение в зеркальных объектах должно меняться во времени. Отметим, что в случае шейдерной визуализации с высоким качеством расчет вектора RCMCS производится в фрагментном шейдере. Однако такие вычисления необходимы только для отражающих объектов, поэтому возникает вопрос: “Как не производить эти расчеты для остальных объектов сцены, если используемое расширение OpenGL не поддерживает организацию ветвлений в шейдере?” Одним из решений этой проблемы является метод статической оптимизации. Наиболее распространенными расширениями OpenGL для работы с шейдерами являются ARB_vertex_program и ARB_fragment_program (стандарт компании Architecture Review Board), так как они поддерживаются практически на всех типах современных видеоадаптеров. Однако эти расширения не дают возможности реализовывать ветвления в вершинных и фрагментных программах, поскольку используют первую версию шейдеров (!!ARBvp1.0 и !!ARBfp1.0), которая не предусматривает ветвлений. Эту проблему можно решить, используя дополнительную опцию внутри вершинной и фрагментной программ, например, NV_vertex_program2 и NV_fragment_program2. Однако применение данных опций резко сужает круг видеокарт, на которых будут работать шейдерные программы (в случае NV_vertex_program2 и NV_fragment_program2 – только на видеоадаптерах nVidia, начиная с серии nv40). Кроме того, время выполнения одного стандартного оператора ветвления IF в шейдерных программах эквивалентно времени одной инструкции. Если необходимо организовать несколько ветвлений в пиксельных шейдерах, то при рендеринге в каждом кадре для каждого пиксела будут выполняться несколько дополнительных инструкций, что в сумме составит уже ощутимое время. Это особенно важно, когда сцену надо визуализировать в реальном режиме времени. Другой способ решения проблемы состоит в использовании нескольких вершинных и фрагментных программ, каждая из которых будет соответствовать тем или иным условиям. Этот способ тоже имеет большой минус – при большом количестве условий мы получим множество файлов с шейдерными программами, которые могут мало отличаться друг от друга. При этом при внесении изменений или добавлений в общие части программ нужно идентично корректировать код в каждом из имеющихся файлов. Решением вопроса может стать применение метода статической оптимизации вершинных и фрагментных шейдеров. Идея метода статической оптимизации состоит во введении ветвлений, описание которых использует специальный мета-язык, в шейдерную программу, в их обработке исходя из известных условий на этапе, предшествующем загрузке, и в подключении этой программы. Реализацией метода является подпрограмма, или функция-оптимизатор, которая получает в качестве входных параметров шейдерную программу, содержащую ветвления, и некоторый вектор условий, определяющий, по каким из ветвей в программе должен осуществляться переход. Выходом функции является оптимизированная под заданные условия программа, не включающая в себя ветвления (рис. 5). При этом получается, что существует только один файл с вершинной (фрагментной) программой, содержащей ветвления, которая автоматически преобразуется в нужное количество программ, соответствующих требуемым условиям и не содержащих ветвления. Блок-схеме (рис. 5) могут соответствовать различные программные реализации, рассмотрим одну из них. Пусть вершинная (фрагментная) программа содержит ветвления, имеющие синтаксис: @IF условие1 [условие2 [ … [условиеN] …]]; #блок команд, выполняющихся при соблюдении хотя бы одного из условий 1..N … [ @ELSE; #блок команд, выполняющихся при несоблюдении всех условий 1..N … ] @ENDIF; Здесь знак @ показывает, что строка программы содержит специальный оператор IF, ELSE или ENDIF; N – количество условий, а в квадратных скобках указаны необязательные элементы. Условия могут также начинаться с оператора отрицания “!”, например, !условие1. В частности, если нужно предусмотреть различные алгоритмы расчета освещенности при наличии и отсутствии зеркального освещения, можно написать: @IF SPECULAR; #блок команд для расчета зеркального освещения … @ENDIF; Тогда, если условие SPECULAR соблюдается, то есть имеет место зеркальная составляющая освещения, команды до @ENDIF должны выполняться, в противном случае – игнорироваться. Вектор условий запишем в виде строки типа CString: ²[условие1 [условие2 [… [условиеM] …]]², где в квадратных скобках указаны необязательные элементы; M – количество условий в строке, причем в общем случае M¹N. Например, вектор, определяющий условие наличия у объекта bump-текстуры и зеркальное освещение (specular lighting) этого объекта от направленного источника типа “прожектор” (spot light), может иметь вид: ²BUMP SPECULAR SPOT².
Алгоритм функции статической оптимизации LoadProgramWithStaticOptimization можно коротко описать следующим образом. 1. Пока не найден условный оператор @IF или команда END, строки вершинной (фрагментной) программы копируются в выходную строку p_string. 2. При нахождении оператора @IF осуществляется поиск стоящих при нем условий во входной строке cond_vec (conditions vector). При нахождении хотя бы одного из них поиск прекращается, специальный флаг F взводится в 1, и в p_string добавляются все строки программы до @ELSE (если такой оператор есть, иначе – до @ENDIF). Если среди этих строк вновь найдена строка с оператором @IF, то имеет место рекурсия, и алгоритм возвращается к началу пункта 2. Если ни одно из условий не найдено в строке cond_vec, то все строки программы до @ENDIF (@ELSE) пропускаются. Надо отметить, что наличие перед условием оператора “!”, изменяет ход алгоритма: если такое условие найдено в cond_vec, то оно рассматривается как ненайденное, и наоборот. 3. Если найден оператор @ELSE и при этом флаг F=0, то все строки программы до @ENDIF добавляются к p_string, если F=1 – игнорируются. 4. Выполняются шаги 2 и 3, пока не будут обработаны все вложенные операторы @IF, после чего осуществляется переход к шагу 1. Отметим, что практически любая вложенность условных операторов @IF поддерживается приведенным алгоритмом. | ||||||||||||||||||||||||||||||||
http://swsys.ru/index.php?id=331&lang=%E2%8C%A9%3Den&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Алгоритмы и программное обеспечение системы обработки топопланов
- Реализация теней с помощью библиотеки OpenGL
- Знания в интеллектуальных системах
- Информационная поддежка технического обеспечения кораблей при первой операции флота

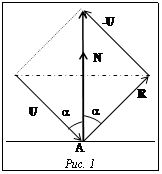 Первый способ предполагает наличие шести заранее подготовленных двухмерных текстур, образующих кубическую карту среды. Для каждой видимой точки А на поверхности объекта в видовой системе координат (VCS) вычисляется вектор отражения R=RVCS на основе единичного вектора U, направленного из начала видовой системы в точку А и единичной нормали N в точке А. По закону отражения, можно написать следующее равенство: 2 ||U|| Cosa · N=R–U (рис. 1).
Первый способ предполагает наличие шести заранее подготовленных двухмерных текстур, образующих кубическую карту среды. Для каждой видимой точки А на поверхности объекта в видовой системе координат (VCS) вычисляется вектор отражения R=RVCS на основе единичного вектора U, направленного из начала видовой системы в точку А и единичной нормали N в точке А. По закону отражения, можно написать следующее равенство: 2 ||U|| Cosa · N=R–U (рис. 1).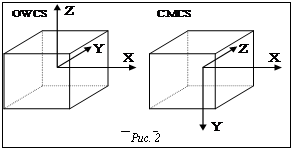 Так как векторы в 3D-аффинном пространстве имеют нулевую четвертую координату, то в качестве MV можно брать матрицу 3´3, осуществляющую только поворот системы координат и не учитывающую переноса. В таком случае (MV)-1 совпадает с транспонированной матрицей (MV)Т. Если использовать аппаратное умножение векторов размерности 4, то к матрице MV можно добавить строку и столбец вида (0,0,0,1).
Так как векторы в 3D-аффинном пространстве имеют нулевую четвертую координату, то в качестве MV можно брать матрицу 3´3, осуществляющую только поворот системы координат и не учитывающую переноса. В таком случае (MV)-1 совпадает с транспонированной матрицей (MV)Т. Если использовать аппаратное умножение векторов размерности 4, то к матрице MV можно добавить строку и столбец вида (0,0,0,1). ,
, .
. Для остальных случаев выбор грани куба и расчет для нее текстурных координат производятся аналогично (подробнее см.: А.В. Мальцев, М.В. Михайлюк. Технология рельефного текстурирования в системах визуализации. // Сб. докл. науч. конф., посвящ. 45-летию выхода человека в космос. М. 2006).
Для остальных случаев выбор грани куба и расчет для нее текстурных координат производятся аналогично (подробнее см.: А.В. Мальцев, М.В. Михайлюк. Технология рельефного текстурирования в системах визуализации. // Сб. докл. науч. конф., посвящ. 45-летию выхода человека в космос. М. 2006). Пункт 1 предполагает введение в сцену шести виртуальных камер, расположенных в центре объекта и сонаправленных с осями +X и -X, +Y и -Y, +Z и –Z мировой системы координат (рис. 4). Угол раствора камер должен составлять 90°. Рассмотрим, например, вычисление видовой матрицы для камеры, снимающей по направлению –Z в системе ОWCS.
Пункт 1 предполагает введение в сцену шести виртуальных камер, расположенных в центре объекта и сонаправленных с осями +X и -X, +Y и -Y, +Z и –Z мировой системы координат (рис. 4). Угол раствора камер должен составлять 90°. Рассмотрим, например, вычисление видовой матрицы для камеры, снимающей по направлению –Z в системе ОWCS. ,
,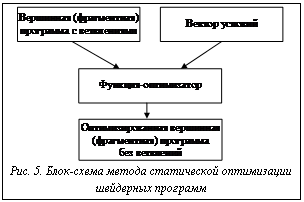 Функция-оптимизатор имеет интерфейс: void LoadProgramWithStaticOptimization(FILE* file, CString& p_str, CString& cond_vec), где file – указатель на файл, содержащий вершинную (фрагментную) программу; p_str – строка, в которую будет записана оптимизированная программа (результат функции-оптимизатора); cond_vec – вектор условий.
Функция-оптимизатор имеет интерфейс: void LoadProgramWithStaticOptimization(FILE* file, CString& p_str, CString& cond_vec), где file – указатель на файл, содержащий вершинную (фрагментную) программу; p_str – строка, в которую будет записана оптимизированная программа (результат функции-оптимизатора); cond_vec – вектор условий.