Интеграция технологии OLAP и нечетких множеств для обработки неопределенных и неточных данных в системах поддержки принятия решений
| Еремеев А.П. (eremeev@appmat.ru) - Национальный исследовательский университет «Московский энергетический институт» (профессор), г. Москва, Россия, доктор технических наук, Еремеев А.А. (eremeev@appmat.ru) - Московский энергетический институт (технический университет), г. Москва, Россия | |
| Ключевые слова: нечеткие множества., технология olap, хранилище данных, интеллектуальная система |
|
| Keywords: fuzzy sets, OLAP technology, data warehouse, intellectual system |
|
|
|
|
Современные интеллектуальные системы (ИС), ориентированные на открытые и динамические предметные (проблемные) области, представителем которых являются ИС поддержки принятия решений реального времени (ИСППР РВ) [1], оперируют, как правило, большими массивами быстро изменяемых данных, поступающих из различных внешних источников (датчиков, сенсоров, оператора или непосредственно от ЛПР), то есть имеют дело с динамической информацией, для поддержки которой необходима соответствующая организация баз данных и знаний. ИСППР РВ должны иметь средства для комплексного многомерного анализа больших объемов данных, их динамики и тенденций [2]. Для этого предлагается использовать технологию OLAP [3]. Хотя технология OLAP и не является необходимым атрибутом хранилищ данных (ХД) (Data Warehouses), в настоящее время она активно применяется для анализа накопленной в ХД информации.
В процессе анализа данных в ИСППР РВ часто возникает необходимость построения зависимостей между различными параметрами, число которых может быть значительным. Возможность такого анализа требует представления данных в виде многомерной модели – гиперкуба, или OLAP-куба, содержащего одно или более измерений и представляющего собой упорядоченный набор ячеек (рис. 1). Каждая ячейка определяется одним и только одним набором значений измерений – меток. Под измерением понимается множество меток, образующих одну из граней гиперкуба. Примером временного (темпорального) измерения является список дней, месяцев, кварталов. Примером географического измерения может быть перечень территориальных объектов: населенных пунктов, районов, регионов, стран и т.д. Для получения доступа к данным пользователю необходимо указать одну или несколько ячеек путем выбора значений измерений, которым соответствуют необходимые ячейки. Процесс выбора значений измерений называется фиксацией меток, а множества выбранных значений измерений – множеством фиксированных меток. Используем следующие обозначения: OLAP-куб данных обозначается как множество ячеек H(D, M), где D={d1, d2, …, dn} – множество измерений гиперкуба; Ценность и достоверность знаний, полученных в результате интеллектуального анализа данных, зависят как от эффективности используемых аналитических методов и алгоритмов, так и от правильно подобранных и подготовленных для анализа исходных данных. Чтобы довести данные до приемлемого уровня качества и информативности, а также органи- зовать интегрированное хранение данных в структурах, обеспечивающих их целостность, непротиворечивость, высокую скорость и гибкость вы- полнения аналитических запросов, необходимо выполнить ряд процедур, называемых консолидацией. Консолидация – комплекс методов и процедур, направленных на извлечение данных из различных источников (ХД, БД и т.п.), обеспечение необходимого уровня их информативности и качества, преобразование в единый формат, в котором они могут быть загружены в ХД или аналитическую систему. Консолидация данных является начальным этапом реализации любой аналитической задачи или проекта. В ее основе лежит процесс сбора и организации хранения данных в виде, оптимальном с точки зрения их обработки на конкретной аналитической платформе или решения конкретной аналитической задачи. Сопутствующими задачами консолидации являются оценка качества данных и их обогащение. Основными критериями оптимальности (относительно консолидации данных) являются обеспечение высокой скорости доступа к данным, компактность хранения, автоматическая поддержка целостности структуры данных, контроль непротиворечивости данных.
Еще один пример эффективного обогащения (путем интеграции) одной технологии (ХД) другой (нечеткая логика) демонстрируют нечеткие срезы – фильтры по измерениям, в которых фигурируют нечеткие величины, например «все молодые ученые с небольшим доходом». Напомним, что в реляционных БД эту роль выполняют нечеткие запросы, предложенные в работах Д. Дюбуа и Г. Прада. Информация в ХД присутствует обычно в четком виде, поэтому для использования в фильтрах нечетких понятий нужно предварительно представить их в виде нечетких множеств. Формирование нечетких срезов Лингвистические переменные можно задать для любого измерения, атрибута измерения или факта, значения которого имеют непрерывный вид. Их параметры – названия, терм-множества, параметры функций принадлежности – будут содержаться в семантическом слое ХД (рис. 2).
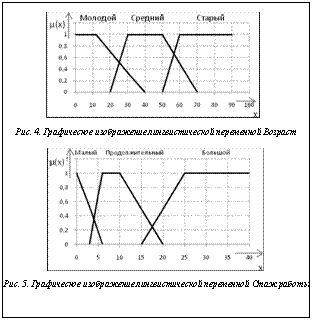
Алгоритм формирования нечеткого среза представлен на рисунке 3. На шаге 1 используется семантический слой ХД. На шаге 3 в результирующий SQL-запрос попадают границы с учетом минимального индекса соответствия а. Шаг 5 предполагает применение нечетких логических операций. Рассмотрим пример. Пусть в ХД содержится информация о соискателях вакансий и срез (четкий) по измерениям Код анкеты, Возраст и Стаж работы обеспечивает набор данных, представленный в таблице 1. Очевидно, что Код анкеты – это служебное поле. Для Возраста будем использовать лингвистическую переменную (рис. 4), а для поля Стаж работы – переменную, определенную на рисунке 5. При задании функций принадлежности используются следующие множества: Малый – {0; 0; 6}, Продолжительный – {3; 6; 10; 20}, Большой – {15; 25; 40; 40}. Таблица 1 Информация о соискателях (срез по измерениям Возраст и Стаж работы)
Определим нечеткий срез «Возраст = Средний и Стаж работы = Продолжительный». Например, для анкеты 4 (см. табл. 1) получим:
Аналогично рассчитываются степени принадлежности к итоговому нечеткому множеству для каждого претендента. Зададим минимальный индекс соответствия, равный 0,3, и получим результат, показанный в таблице 2. Таблица 2 Результат нечеткого среза
Возможны ситуации, когда аналитику (ЛПР) требуется не только извлечь информацию, оперируя нечеткими понятиями, но и проранжировать ее по убыванию (возрастанию) степени релевантности запроса. В этих случаях нечеткий поиск в ХД является наиболее предпочтительным и позволяет ответить на следующие вопросы: каких клиентов обзвонить в первую очередь, кому сделать рекламное предложение и т.д.
Анализ неточных данных и обобщение многомерной модели данных В контексте представления неоднозначных (неточных и неопределенных) данных необходимо рассмотреть расширение многомерной модели данных OLAP, а также анализ возможной семантики для агрегации запросов по таким данным [5]. Рассмотрим несколько критериев, которые должны быть удовлетворены при любом подходе к обработке неоднозначных данных в OLAP. Первый критерий – непротиворечивость (consistency), используемый для установления отношений между подобными запросами, формируемыми в связанных узлах доменной иерархии и позволяющими пользователям осуществлять ожидаемую навигацию вверх и вниз по иерархии. Второй критерий – верность (faithfulness), гарантирующий то, что точные данные должны привести к лучшим результатам. Третий критерий – сохранение корреляции (correlation-preservation), по существу требующий, чтобы статистические свойства данных не влияли на распределение неоднозначных записей данных. Расширим обычную модель данных OLAP следующим образом. Прежде всего ослабим ограничение, согласно которому атрибуты размерности в факте должны быть назначены из конечного множества значений основной области, чтобы смоделировать неточность. Второе расширение должно представить новый вид атрибута меры – неопределенность. Таким образом, неопределенное значение – это диапазон возможных значений вместе с вероятностью каждого из них. В частности, можно представить значение для неуверенной меры как функцию распределения вероятностей (probability distribution function, PDF) по значениям от основной области. Подытоживая сказанное, в плане интеграции технологии OLAP и аппарата нечетких множеств для обработки неоднозначных данных в ИСППР РВ предлагаются обобщение OLAP-модели для возможности представления неоднозначности в данных как в случае неточных значений размерности, так и в случае неопределенных значений меры, а также введение ряда критериев (непротиворечивость, верность, сохранение корреляции), направленных на выбор наиболее подходящей семантики для агрегации запросов по неоднозначным данным. Рассмотрим обобщение стандартной многомерной модели данных, включающей неточности и неопределенности. Атрибуты в стандартной модели OLAP могут быть двух видов – измерения и метки. Расширим модель с целью учета неопределенности в измерении величин и погрешности в измерении значения. Пусть неопределенная область U, заданная на основной области (универсуме) O, есть множество всех возможных функций распределения вероятности (PDF) на O [5]. Таким образом, каждое значение u в U есть PDF, указывающая на степень уверенности в том, что истинное значение будет представлено как o для каждого oÎO. Неточная область I на основной области B является подмножеством множества B, а элементы области I называются неточными значениями, ÆÏI В OLAP каждое измерение имеет соответствующую иерархию, например, размерность расположения может иметь атрибуты Города и Области, где Области – обобщение для Городов, что свидетельствует об особых случаях неточных областей, называемых иерархическими областями. Иерархическая область H на основной области B определяется как неточная область на B, такая, что H содержит все одноэлементное множество (то есть соответствует некоторому элементу B) и для любой пары элементов h1, h2ÎH, h1Êh2 или h1Çh2=Æ. Таким образом, каждый одноэлементный узел есть вершина в иерархической области H, а каждый неодноэлементный узел в H – неконечный узел. Например, Южный административный округ (АО), Западный АО и т.д. – конечные узлы с родителем Москва, для которого (узла), в свою очередь, родителем является Россия. Схема таблицы фактов есть схема áA1, …, Ak; M1, …, Mnñ, где размерность атрибута Ai , iÎ1, …, k, имеет соответствующую неточную область определения dom(Ai), а размерность атрибута Mj, jÎ1, …, n – область определения dom(Mj), которая может быть числовой или неточной. Экземпляром БД такой схемы таблицы фактов является коллекция фактов вида áa1, …, ak; m1, …, mnñ, где aÎdom(Ai), iÎ1, …, k, и mjÎdom(Mj), jÎ1, …, n. В частности, если dom(Ai) является иерархической областью, ai может быть любым конечным или неконечным узлом в dom(Ai). Рассмотренное обобщение многомерной модели данных позволяет представлять неточные данные и реализовать алгоритмы для оценки агрегации запросов. В настоящее время довольно активно ведутся исследования по интеграции технологии OLAP с другими различными технологиями, в частности с нечеткими моделями. В статье рассмотрены возможности интеграции технологии OLAP с аппаратом нечетких множеств (нечетких срезов) в плане использования соответствующих методов и программных средств в ИСППР РВ для анализа и оперирования плохо определенной (неоднозначной) информацией (данными и знаниями). Базовые программные модули предложенной интеграции технологии OLAP и нечетких моделей реализуются на кафедре прикладной математики МЭИ в исследованиях, касающихся разработки методов, моделей и базовых инструментальных средств конструирования ИСППР РВ семиотического типа на основе нетрадиционных логик. В дальнейших исследованиях и разработках планируется рассмотреть использование концепции возможных миров (possible worlds) при неоднозначности данных, позволяющей реализовать новый, основанный на распределении подход к определению семантики запросов агрегации и глубокому анализу вариантов, возникающих при обработке неоднозначности данных, используя критерии непротиворечивости, верности и сохранения корреляции. Кроме того, представляют интерес алгоритмы для оценки агрегации запросов (для обычных и для неточных мер), а также сложности анализа и метод многомерного анализа данных на основе технологии так называемых недоопределенных вычислений [6]. Литература 1. Вагин В.Н., Еремеев А.П. Некоторые базовые принципы построения интеллектуальных систем поддержки принятия решений реального времени // Изв. РАН. Теория и системы управления. 2001. № 6. С. 114–123. 2. Еремеев А.А., Еремеев А.П., Пантелеев А.А. Темпоральная модель данных и возможности ее реализации на основе технологии OLAP // 12-я национальная конференция по искусственному интеллекту с международным участием КИИ-2010 (20–24 сентября 2010 г., г. Тверь, Россия): тр. конф. М.: Физматлит, 2010. Т. 3. С. 345–353. 3. Codd E.F., Codd S.B., Salley C.T., Providing OLAP to User-Analysts: an IT Mandate, Arbor Software Corp. Papers, 1996. 4. Еремеев А.П., Еремеев А.А., Пантелеев А.А. Возможности реализации темпоральной базы данных для интеллектуальных систем // Программные продукты и системы. 2011. № 2. С. 3–7. 5. Burdick D., Deshpande P.M., Jayram T.S., Ramakrishnan R. and Vaithyanathan S. The VLDB Journal, 2007, Vol. 16, no. 1, pp. 123–144. 6. Смирнов К.Е. Многомерный анализ данных в системах недоопределенных вычислений // Программные продукты и системы. 2010. № 4. С. 71–74. |
http://swsys.ru/index.php?id=3371&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Возможности реализации темпоральной базы данных для интеллектуальных систем
- Система назначения персонифицированного лечения по аналогии на основе гибридного способа извлечения прецедентов
- Интеллектуальная система, основанная на многоуровневой онтологии химии
- Реализация экспертной системы для оценки инновационности технических решений
- Прототип диагностической системы поддержки принятия решений на основе интеграции байесовских сетей доверия и метода Демпстера–Шефера

 Согласно данной технологии, оперативная информация (данные) собирается из различных источников, очищается, интегрируется и складывается в реляционное ХД. Затем данные подготавливаются для OLAP-анализа. Они могут быть загружены в специальную БД OLAP или оставлены в реляционном ХД. Важнейшим элементом являются метаданные – информация о структуре, размещении и трансформации данных. Благодаря им обеспечивается эффективное взаимодействие различных компонентов ХД.
Согласно данной технологии, оперативная информация (данные) собирается из различных источников, очищается, интегрируется и складывается в реляционное ХД. Затем данные подготавливаются для OLAP-анализа. Они могут быть загружены в специальную БД OLAP или оставлены в реляционном ХД. Важнейшим элементом являются метаданные – информация о структуре, размещении и трансформации данных. Благодаря им обеспечивается эффективное взаимодействие различных компонентов ХД. – множество меток гиперкуба;
– множество меток гиперкуба;  , i=1, …, n – множество меток измерения di; D¢ÍD – множество фиксированных измерений; M¢ÍM – множество фиксированных меток [3]. Подмножество OLAP-куба, соответствующее множествам фиксированных значений D¢, M¢ обозначается как H¢(D¢, M¢). Каждой ячейке OLAP-куба hÎH соответствует единственно возможный набор меток измерений MhÌM. Ячейка может быть пустой (не содержать данных) или содержать значение показателя – меру. Множество мер OLAP-куба H(D, M) обозначается V(H).
, i=1, …, n – множество меток измерения di; D¢ÍD – множество фиксированных измерений; M¢ÍM – множество фиксированных меток [3]. Подмножество OLAP-куба, соответствующее множествам фиксированных значений D¢, M¢ обозначается как H¢(D¢, M¢). Каждой ячейке OLAP-куба hÎH соответствует единственно возможный набор меток измерений MhÌM. Ячейка может быть пустой (не содержать данных) или содержать значение показателя – меру. Множество мер OLAP-куба H(D, M) обозначается V(H). Для повышения уровня качества и информативности данных применяется интеграция различных технологий, например, в работе [4] рассматривается возможность интеграции темпоральных БД, оперирующих с данными, актуальными в определенный момент времени или на некотором временном интервале, с ХД и технологией OLAP.
Для повышения уровня качества и информативности данных применяется интеграция различных технологий, например, в работе [4] рассматривается возможность интеграции темпоральных БД, оперирующих с данными, актуальными в определенный момент времени или на некотором временном интервале, с ХД и технологией OLAP.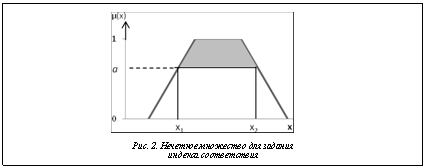 Результатом выполнения нечеткого среза, помимо самого подмножества ячеек гиперкуба, удовлетворяющих заданным условиям, является индекс соответствия срезу CIÎ[0, 1]. По сути это итоговая степень принадлежности к нечетким множествам измерений и фактов, участвующих в сечении куба, которая рассчитывается для каждой записи набора данных. Для ускорения выполнения запросов к ХД задают верхнюю границу a индекса соответствия CI >а, что позволяет уже на уровне SQL-запроса отсеять записи, заведомо не удовлетворяющие минимальному порогу индекса соответствия. На рисунке 2 показано, что элементы нечеткого множества со значениями в интервале [x1, x2] обеспечат степень принадлежности не ниже а.
Результатом выполнения нечеткого среза, помимо самого подмножества ячеек гиперкуба, удовлетворяющих заданным условиям, является индекс соответствия срезу CIÎ[0, 1]. По сути это итоговая степень принадлежности к нечетким множествам измерений и фактов, участвующих в сечении куба, которая рассчитывается для каждой записи набора данных. Для ускорения выполнения запросов к ХД задают верхнюю границу a индекса соответствия CI >а, что позволяет уже на уровне SQL-запроса отсеять записи, заведомо не удовлетворяющие минимальному порогу индекса соответствия. На рисунке 2 показано, что элементы нечеткого множества со значениями в интервале [x1, x2] обеспечат степень принадлежности не ниже а.
 С помощью аппарата нечетких множеств и методов извлечения нечетких данных реализуется расширение понятия OLAP-куба, что позволяет исследовать возможность представления неточных данных в OLAP.
С помощью аппарата нечетких множеств и методов извлечения нечетких данных реализуется расширение понятия OLAP-куба, что позволяет исследовать возможность представления неточных данных в OLAP. Интуитивно понятно, что неточное значение имеет непустое множество возможных значений. Разрешение атрибутам измерения иметь неточную область позволяет, например, использовать неточное (обобщенное) значение Москва для атрибута расположения в записи данных, если известно, что некое событие произошло в Москве, но неизвестно, в каком районе.
Интуитивно понятно, что неточное значение имеет непустое множество возможных значений. Разрешение атрибутам измерения иметь неточную область позволяет, например, использовать неточное (обобщенное) значение Москва для атрибута расположения в записи данных, если известно, что некое событие произошло в Москве, но неизвестно, в каком районе.