Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Применение технологии CUDA для симуляции частиц при параллельном программировании
Аннотация:Изложен метод симуляции частиц, находящихся во взаимодействии, с помощью технологии параллельного про-граммирования CUDA. Рассматриваются математическая постановка задачи при взаимодействии частиц, а также ме-тод дискретных элементов и особенности технологии CUDA. В методе дискретных элементов каждая частица мате-риала представляется как тело из механики Ньютона, имеющее массу и координаты центра, на которое действуют силы. Частицы взаимодействуют друг с другом по определенным законам, и можно наблюдать движение системы в целом. Для удобства введена переменная threadIdx – трехкомпонентный вектор, так что потоки могут быть иденти-фицированы по одно-, двух- и трехмерному индексам, образуя при этом соответственно одно-, двух- или трехмерную сетку потоков. Таким образом обеспечивается прозрачность в работе с такими объектами, как массив, матрица или объемная сетка. Рассматриваются программная реализация предложенных методов и алгоритмов, а также интерфейс, объединяющий все методы и алгоритмы.
Abstract:In article the method of simulation of the particles being in interaction, by means of technology of parallel programming of CUDA is considered. The definition оf interaction of particles is considered. The method of discrete elements is considered of the CUDA technology. In a method of discrete elements each particle l is represented as a body which has weight and center coordinates. Particles interact with each other and it is possible to observe system movement as a whole. The threadIdx variable is a three-component vector. Thus transparence is provided in work with such objects as the massif, a matrix or a volume grid is provided. Program realization is considered, the interface connecting all methods and algorithms together is considered.
| Авторы: Астахова И.Ф. (astachova@list.ru) - Воронежский государственный университет (профессор), Воронеж, Россия, доктор технических наук, Коробкин Е.А. (Evgeniy-voronez@mail.ru) - Воронежский государственный университет (аспирант ), Воронеж, Россия | |
| Ключевые слова: метод дискретных элементов., технология cuda, графический процессор, параллельное программирование |
|
| Keywords: method of discrete elements, cuda technology, graphic processor, parallel programming |
|
| Количество просмотров: 11001 |
Версия для печати Выпуск в формате PDF (5.29Мб) Скачать обложку в формате PDF (1.21Мб) |
Гранулированные материалы, такие как песок, грунт, порошок или зерно, являются неотъемлемой частью нашего мира, поэтому существует потребность в создании симуляции динамики таких материалов: например, в горнодобывающей промышленности для изучения самообрушения пород, в сельскохозяйственной отрасли – поведения зерна в каналах. Способ симуляции сыпучих сред описывает метод дискретного элемента (МДЭ) [1, 2]. В нем каждая частица материала представляется как тело из механики Ньютона, которое имеет массу и координаты центра и на которое действуют силы. Таким образом, частицы взаимодействуют друг с другом по определенным законам и можно наблюдать движение системы в целом. Существует несколько комплексов приложений для моделирования частиц с помощью МДЭ. Примером могут служить Open Source проекты LIGGGHTS и Yade, которые решают целый спектр научных задач, связанных с МДЭ. Устройства находятся в широком доступе, а их мощностей хватает для небольших научных исследований с участием сотен тысяч частиц, тогда как центральный процессор (ЦП) можно использовать для расчета очень небольших систем за приемлемое время. Технология CUDA, созданная компанией NVIDIA, предоставляет интерфейс низкого уровня для решения задач программирования в параллельной среде с помощью видеокарт NVIDIA и идеально подходит для целей данной работы. Авторы, используя архитектуру параллельных вычислений CUDA, реализовали программное и аппаратное обеспечение, позволяющее производить симуляцию гранулированных частиц. В статье проведена оценка производительности такого программного комплекса относительно классических способов реализации, использующих в качестве основной вычислительной единицы ЦП. Технология CUDA Эта технология использует мощности графических процессоров (ГП) [3, 4]. Подобные устройства оптимизированы для работы с числами с плавающей точкой одинарной точности; их архитектура значительно отличается от архитектуры ЦП. Так, ГП более сконцентрированы на вычислениях, чем на контроле выполнения (условные переходы) и кэшировании данных. Также ГП ориентируются на параллельные вычисления, поэтому данные устройства являются периферийными для решения конкретных вычислительных задач, которые можно выполнять в параллельной среде, при этом основная логика приложения осуществляется на ЦП. Для масштабируемости технологии CUDA вводятся три ключевые абстракции: иерархия групп потоков, разделенная память и барьерная синхронизация. Программист должен разделить задачу на несколько подзадач, которые выполняются независимо разными блоками потоков, реализующими, в свою очередь, небольшую часть этой подзадачи. Разделенная память и синхронизация позволяют потокам работать вместе. Масштабируемость достигается за счет того, что блок может быть выполнен на любом ядре ГП, в любой последовательности, параллельно или последовательно, так что программа выполнима на любом количестве доступных ядер. CUDA расширяет язык C, вводя понятие ядер – функций на языке С, которые при вызове выполняются N раз на N различных потоках CUDA. Ядро определяется с помощью приставки __global__, а количество потоков – с помощью нового синтаксиса конфигурации запуска <<<…>>>. Каждый поток, выполняемый ядром, получает уникальный индекс, доступ к которому можно получить через встроенную переменную threadIdx. Для удобства переменную threadIdx обозначим как трехкомпонентный вектор, поэтому потоки могут быть идентифицированы по одно-, двух- и трехмерному индексам, образуя при этом соответственно одно-, двух- или трехмерную сетку потоков. В результате обеспечивается прозрачность в работе с такими объектами, как массив, матрица или объемная сетка. Количество потоков в блоке ограниченно, потому что все потоки должны быть расположены в пределах одного процессорного ядра. В настоящее время максимальное количество потоков на блок 1 024. Однако ядро может быть выполнено на нескольких блоках, что, само собой, приумножит количество потоков. Блоки также организованы в одно-, двух- или трехмерную сетку. Каждый блок в сетке может быть идентифицирован одно-, двух- или трехмерным индексом, доступ к которому в ядре возможен через переменную blockIdx. Размерность блока можно узнать из переменной blockDim. Блоки должны быть независимыми: могут запускаться в любом порядке, параллельно или последовательно. Это необходимо для того, чтобы каждый блок мог быть запланирован на любом процессорном ядре независимо от их количества, что позволяет писать код, масштабируемый по мере увеличения количества ядер. Иерархия памяти Потоки CUDA могут иметь доступ к различным пространствам памяти. У каждого потока свое локальное пространство памяти. Каждый блок потоков имеет разделенную память, которая видима всем потокам этого блока. Все потоки имеют доступ к единой глобальной памяти. Существуют еще два источника данных только для чтения – текстурная и константная память. Глобальная, текстурная и константная память оптимизированы для различных действий. Текстурная память также позволяет производить фильтрацию данных для некоторых форматов. В терминах CUDA ЦП – хост, а ГП – девайс. Без хоста невозможно функционирование параллельного приложения, так как сама программа по-прежнему выполняется, используя ЦП, и лишь отдельные фрагменты выполняются на девайсе. Хост и девайс поддерживают собственное пространство в памяти – память хоста и память девайса. Так что программа управляет глобальной, константной и текстурной памятью с помощью обращения к API. Математическая постановка задачи Для каждой i-й частицы задаются ее центр xi, масса mi и радиус ri. Масса mi=rVi, где Vi – объем i-й частицы, легко вычисляемый для шара, который ограничен сферой: V=4/3 pR3. По законам Ньютона движение такой частицы описывается дифференциальным уравнением При моделировании движения гранулированных материалов рассматривается взаимодействие между двумя частицами, поэтому далее приво- дятся общие формулы для пары частиц, которые используются уже в конкретном случае. Пусть координаты центров каждой из них будут соответственно x1 и x2, их массы – m1 и m2, радиусы сфер – r1 и r2. Степень проникновения x двух частиц рассчитывается по формуле x=r1+r2–úêx2–x1úê. Если x<0, то две частицы находятся на некотором расстоянии друг от друга и действующие на них силы в принятой модели не рассматриваются. При x=0 действуют силы трения, а при x>0 частицы перекрываются и дополнительное действие оказывают силы отталкивания. Таким образом, для взаимодействия двух частиц i и j необходимо учитывать силу отталкивания Fо и силу трения FТ. Тогда результирующую силу взаимодействия двух частиц можно записать так: Fвз=Fо+FТ. На частицу с центром x1 действует сила Fвз, а на частицу с центром x2 – обратная сила Fвз. Нормализованным вектором N будем называть вектор, указывающий направление от центра x1 до центра x2: Сила отталкивания действует вдоль вектора N, поэтому ее удобно записать через ее модуль fn: Fо=–fnN. Пусть также дана скорость частиц v1 и v2, из них получим относительную скорость V, скорость вдоль нормального вектора NVn и тангенциальную скорость Vt: V=v1–v2, Vn=(V N), Vt=V–VnN. Тогда модуль силы отталкивания fn=knx+kdVn, где kn – коэффициент упругости, получаемый экспериментальным путем; kd – коэффициент демпфирования, который можно получить через коэффициент восстановления после удара c следующим образом: Сила трения в простейшем случае направлена против тангенциальной скорости Vt и равна FТ=–kТVt, где kТ – коэффициент вязкости, похожий на коэффициент демпфирования kd. Однако данный подход не учитывает силу отталкивания. В работе используется модифицированная формула При составлении модели были выделены следующие физические параметры системы: kn – коэффициент упругости, который получается экспериментальным путем, однако в более сложных моделях этот коэффициент может быть выражен через другие физические параметры (модуль Юнга, коэффициент Пуассона); c – коэффициент восстановления после отталкивания (определяет силу отскакивания частицы от поверхности); m – коэффициент трения. Важно заметить, что эти коэффициенты работают при взаимодействии и поэтому зависят от взаимодействующих поверхностей. Частицы взаимодействуют не только друг с другом, но и с окружающими границами, поэтому необходимо иметь два набора таких параметров: одни будут действовать при столкновении частиц, а другие – при столкновении частицы со статической геометрией. Для практической задачи можно добавить промежуточное значение скорости n и вывести следующую систему уравнений:
Используя метод Эйлера для численного дифференцирования, получаем схемы:
где i – номер шага; ∆t – временной шаг (должен быть достаточно небольшим, порядка одной миллионной, чтобы поддерживать стабильность системы). CUDA как средство повышения производительности МДЭ Рассмотрим способ ускорения вычислений, связанных с МДЭ, с помощью CUDA [4]. Система частиц с определенными физическими параметрами помещена в некоторое начальное состояние. Используя вычислительные мощности ГП, необходимо перевести ее в новое состояние. Такой переход системы будем называть циклом системы. Невозможно обрабатывать все частицы в одном блоке. Так как синхронизации между блоками не существует и они должны выполняться независимо друг от друга, необходимо разделить цикл системы на отдельные части и выполнить вычисления в отдельных функциях-ядрах. Выделим две основные части цикла – интегрирование системы и просчет сил взаимодействия. Иными словами, сначала производится движение системы: скорость каждой частицы обновляется в соответствии с силами, которые на нее действуют, а центр перемещается согласно скорости. Затем в новом состоянии просчитываются силы, действующие на частицы по указанным выше формулам. Получившиеся силы используются для интегрирования на следующем шаге. Наивным способом поиска таких пар будет полный перебор: каждая частица в своем потоке проверяет расстояние до других частиц; если степень проникновения x³0, то необходимо произвести расчет сил взаимодействия. Данный алгоритм имеет сложность O(n2), что абсолютно неприемлемо, так как n – число порядка сотен тысяч. Большинство частиц находятся на относительно большом расстоянии друг от друга. Для данной частицы лишь небольшое количество других частиц находится рядом с ней, а производить расчет сил с другими частицами нет необходимости. Чтобы отсечь эти частицы, пространство делится на ячейки одинакового размера, образуя при этом сетку. Каждая такая ячейка содержит объекты, которые в ней находятся. Так как для каждой частицы можно узнать место ее нахождения, то легко можно узнать, какие частицы находятся вместе с ней. Для простоты количество ячеек в сетке одинаково по всем трем измерениям. Ячейка задается координатами и представляет собой куб со стороной l, которая определяется диаметром. Когда частица находится в данной ячейке, необходимо проверять только частицы, находящиеся в 26 окружающих ее ячейках. Обычно каждая ячейка – это линейный список объектов, которые в ней находятся. Звено такого списка состоит из двух полей – данные и указатель на следующий элемент. Звенья расположены в свободной памяти. Однако с точки зрения технологии CUDA это ведет к нерациональному использованию памяти. Дело в том, что пропускная способность памяти является узким местом всех приложений, использующих эту технологию. Предлагаются следующие способы оптимизации доступа к глобальной памяти – кэширование данных в разделенной памяти и линейный доступ к данным. Помимо глобальной памяти (основного хранилища данных во время вычислений), существует еще разделенная память, доступная всем потокам в пределах блока. Это память небольшого размера, но доступ к ней осуществляется гораздо быстрее. Встроенные средства синхронизации позволяют использовать разделенную память как кэш данных: каждый поток загружает немного данных из глобальной памяти в разделенную, затем все потоки используют только разделенную память. Это сокращает количество обращений к глобальной памяти и ведет к ускорению работы приложения в целом. Глобальная память оптимизирована таким образом, чтобы максимизировать производительность линейного доступа к данным. Несколько запросов к данным объединяются в одну транзакцию, если они вмещаются в один сегмент, размер которого зависит от запрашиваемых данных. Таким образом, если несколько потоков выбирают данные, расположенные друг за другом, то эти данные выбираются за один раз. Если все данные расположены в случайном порядке, то количество транзакций увеличивается, что ведет к снижению производительности. Авторы предлагают модифицированный метод хранения частиц в ячейках, в результате которого алгоритм основного цикла приобретает следующий вид. 1. Выполнить шаг системы с текущими значениями сил. Для каждой частицы найти номер ячейки, в которой она находится. 2. Отсортировать частицы по номеру ячейки. 3. Для каждой ячейки найти ее начало в списке и конец. 4. Произвести расчет сил взаимодействия и перейти к шагу 1. 5. Выполнить шаг системы с текущими значениями сил. Для каждой частицы найти номер ячейки, в которой она размещается. 6. Отсортировать частицы по номеру ячейки. 7. Для каждой ячейки найти ее начало в списке и конец. 8. Произвести расчет сил взаимодействия и перейти к шагу 1. Для работы с технологией CUDA необходим графический процессор, который ее поддерживает. Все ГП компании NVIDIA, начиная с серии 8800, поддерживают данную технологию. Однако более новые модели поддерживают более новую версию CUDA 2.1, которая имеет расширенные возможности. В качестве графического процессора выбрана видеокарта NVIDIA GeForce GTS 450. Данный ГП имеет относительно невысокую цену, приемлемую производительность и поддерживает последнюю версию технологии. Кроме того, следует установить на компьютер CUDA Toolkit – средства разработчиков. Это пакет из программных продуктов, позволяющий создавать параллельные приложения. Он вклю- чает в себя компилятор, библиотеки времени выполнения, профайлер, а также исчерпывающую справочную информацию. CUDA Toolkit интегрируется в Microsoft Visual Studio, поэтому данное приложение также необходимо (версия 2010). Само приложение является графическим. Трехмерная графика выводится на экран с помощью технологии DirectX 10. Для этого был использован уже опробованный авторами DirectX SDK. В качестве альтернативы можно использовать OpenGL. Приложение состоит из окна консоли и главного графического окна. В окне консоли выводится информация об ошибках и событиях. В результате работы было создано приложение, позволяющее выполнять симуляцию частиц с помощью метода дискретных элементов, используя архитектуру параллельных вычислений CUDA. Выявлено, что с помощью данной технологии производительность МДЭ можно увеличить на порядок по сравнению с классическими решениями, использующими центральный процессор. В архитектуру CUDA изначально включена возможность масштабирования, а благодаря доступности данная технология претендует на широкое использование в самых различных сферах научной и повседневной деятельности. Литература 1. Боресков А.В., Харламов Ф.Ф., Марковский Н.Р., Микушин Д.Н., Мортиков Е.В., Мыльцев А.А., Сахарных Н.А., Фролов В.А. Параллельные вычисления на GPU. Архитектура и программная модель CUDA. М.: МГУ, 2012. 336 с. 2. CUDA. URL: http://www.nvidia.ru/object/cuda_home_ new_ru.html (дата обращения: 25.12.2012). 3. OpenCL: What you need to know// MacWord. URL: http://www.macworld.com/article/11348591/showleopard_opencl.html (дата обращения: 25.12.2012). 4. Линев А.В., Боголепов Д.К., Бастраков С.И. Технологии параллельного программирования для процессоров новых архитектур. М.: МГУ, 2010. 160 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=3403&like=1&page=article |
Версия для печати Выпуск в формате PDF (5.29Мб) Скачать обложку в формате PDF (1.21Мб) |
| Статья опубликована в выпуске журнала № 1 за 2013 год. [ на стр. 146-150 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Система моделирования масс-спектрометра на основе параллельного кода частиц в ячейке
- Использование технологий виртуализации вычислительных и графических серверов при проектировании тренажеров, тренажерно-моделирующих комплексов и систем обучения операторов
- Параллельные процессы и программы: модели, языки, реализация на системах
- Возможности параллельного программирования в математических пакетах
- Решение задачи дифракции электромагнитной волны на экранах произвольной формы с использованием технологии CUDA
Назад, к списку статей




 , где Fi – сумма сил, действующих на частицу, включая силу тяжести:
, где Fi – сумма сил, действующих на частицу, включая силу тяжести:  , где
, где 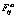 – сила взаимодействия i-й и j-й частиц; Fгр – сила гравитации.
– сила взаимодействия i-й и j-й частиц; Fгр – сила гравитации. .
.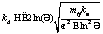 , где
, где  – приведенная масса двух частиц.
– приведенная масса двух частиц.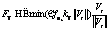 , где m – коэффициент трения. Кроме того, в формуле не учитывается статическое трение.
, где m – коэффициент трения. Кроме того, в формуле не учитывается статическое трение. ,
,  .
. ,
,  ,
,