Journal influence
Bookmark
Next issue
The system of relay programming control seeking for dynamic objects
The article was published in issue no. № 1, 2013 [ pp. 167-171 ]Abstract:In the papera method of terminal control problem for dynamic systems with relay actuator solving is considered. Today, there is no general approach to solve the nonlinear dynamic systems control problem. Moreover, the specific type of control function and the fact that it is non-differentiable causes impossibility of using the classic techniques. The proposed approach is based on the reduction of terminal control problem to the extreme problem on the spaces of real variables and integers. For the reduced problem the modified hybrid evolutionary strategies algorithm has been designed. The new problem definition and the proposed algorithm were the basis for the designing general system of programming control for nonlinear dynamic systems seeking in the form of ideal or multilevel relay. The approbation of the investigated technique for satellite on the geostationary orbit control problem is considered.
Аннотация:Рассматривается метод решения задачи терминального управления динамическими системами, в которых испол-нительный механизм работает по принципу реле. В настоящий момент нет универсального подхода к решению задачи управления для нелинейных динамических систем. Более того, особый вид функции управления, ее недифферен-цируемость свидетельствуют о невозможности применения классических подходов к решению. В данной работе задача управления сведена к задаче поиска экстремума в пространствах действительных и натуральных чисел, для решения которой был модифицирован алгоритм эволюционных стратегий. Это способствовало созданию единой системы нахождения программного управления в виде реле или многоуровневого реле для нелинейных динамических систем. В работе рассматривается применение системы для нахождения управления спутником, находящимся на геостационарной орбите.
| Authors: (ryzhikov-88@yandex.ru) - , Russia, Semenkin E.S. (styugin@rambler.ru) - Academician M.F. Reshetnev Siberian State Aerospace University, Krasnoyarsk, Russia | |
| Keywords: relay, terminal control, control management, dynamic system modeling, evolution strategies |
|
| Page views: 10968 |
Print version Full issue in PDF (5.29Mb) Download the cover in PDF (1.21Мб) |
Задача нахождения программного управления для систем, исполнительным механизмом в которых является идеальное или многоуровневое реле, изучена недостаточно. На сегодняшний день не существует метода нахождения управления в виде кусочно-постоянной функции, что обусловлено не только ее недифференцируемостью, но и тем, что нет единого метода нахождения управления для нелинейных систем. В [1] излагается метод коррекции точек переключения, при этом рассматривается линейная динамическая система, известно число точек переключений и начальное приближение предполагается достаточно близким к решению задачи. В [2] исследуется синтез реле для линейных динамических систем. Задача терминального управления является актуальной и описывается в классических учебниках по оптимальному управлению и в современных работах, например в [3, 4]. В данной работе рассматриваются метод решения экстремальной задачи, к которой была сведена терминальная задача управления, и система нахождения программного управления. Постановка задачи Для системы, описываемой дифференциальным уравнением в общем виде
где Также, если гамильтониан [5] линеен по функции управления, то есть H(x, p, u)=j1(x, p)+j2(x, p)u, а функция управления имеет ограничения по модулю, êu(t)ê Если реле является многоуровневым, функция управления представима в аналогичном виде:
где Пусть Вопрос о выборе числа точек переключения остается открытым, данная постановка задачи и предложенный далее метод решения предполагают неявную настройку количества точек переключения. Прежде всего, если некоторая точка переключения больше конечного времени правления, r>T, то она не влияет на процесс управления. Неявная настройка числа точек переключения обусловлена применением численной схемы интегрирования системы (1). Пусть h – шаг интегрирования, тогда при выполнении условия êri+1–ri–1ê В общем случае решение терминальной задачи для фиксированного времени управления совпадает с решением экстремальной задачи:
где
Существуют также ограничения в виде неравенств
которые обеспечивают выполнение условия нахождения каждой точки переключения внутри интервала [0, T]. В случае использования множества Для решения задачи условной оптимизации введем функцию штрафа
Такие постановки задачи рассматривались в [6]. Добавим еще несколько новых вариантов. Для ограничений ri для любого из критериев (4), (5), (7), (8). В этом случае получаем новые целевые функции, например для (5):
Таким образом, задача терминального управления сводится к задаче оптимизации в пространстве вещественных чисел или вещественных и натуральных чисел с целевыми функциями (3), (4), (6)–(8). Указанные функции многоэкстремальны и не являются аналитически заданными. Учитывая сложность решаемых задач, размерность и неоднородность входных переменных, в качестве алгоритма решения задачи целесообразно выбрать метод эволюционных стратегий [7]. Рассмотрим некоторые особенности работы алгоритма и внесенные модификации. Алгоритм решения экстремальной задачи Пусть каждый индивид задан кортежем
где Особенности задач (3), (4), (6)–(8) задают общий вид набора объективных параметров Для решаемых задач эффективность алгоритма возрастает при использовании измененной операции мутации. Пусть
Пусть Следующая модификация алгоритма обеспечивает выполнение неравенств (5). Каждый объективный параметр задает точку переключения следующим образом: Алгоритм случайного поиска дополняется случайным покоординатным спуском. Из N1 случайно выбранных индивидов случайно выберем N2 объективных хромосом и осуществим N3 шагов локального спуска величиной hl для определения лучшего решения. Гибридизация алгоритма позволяет значительно повысить точность найденных решений и эффективность в целом. В рассмотренных ниже экспериментах эмпирически выбранные настройки алгоритма оптимизации были следующими: размер популяции – 50 индивидов, количество популяций – 50, турнирная селекция с объемом 20 %, дискретное скрещивание, модифицированная мутация с вероятностью для каждого гена 1/úspê. Настройки локального спуска: N1=2×úopê, N2=úopê и N3=5 с шагом hl=0,05. Предложенный алгоритм был проверен на десяти специальных тестовых задачах, что позволило определить наиболее эффективные настройки. Применяя предложенный алгоритм решения оптимизационной задачи для выбранного представления структуры функции управления, может быть решена терминальная задача программного управления. Данный подход реализован в среде OCTAVE/MATLAB и может использоваться для решения любой из представленных задач управления. Так же реализована система решения задачи управления с выбранной пользователем постановкой, дружественным интерфейсом. Система разработана на языке программирования С++, результат решения задачи представляется в виде графиков выхода системы и функции управления. Аналогичные результаты сохраняются в отдельные файлы решения задачи терминального управления, где сохраняются численные решения. Параметры численной схемы интегрирования выбираются пользователем, при этом в программе по умолчанию выбран шаг интегрирования. Примеры решения задач управления Рассмотрим задачу перевода спутника с одной геостационарной орбиты на другую. Координаты спутника описываются нелинейным дифференциальным уравнением вида
Необходимо перевести объект из начального положения x(0)=(1, 0, 1, 0,785) в конечное x(T)= =(1, 0, 1, T) за конечное время T.
Рассмотрим задачу нахождения программного управления для случая, когда амплитуда реле является искомой, то есть задачу синтеза регулирующего устройства. Решение таких задач может быть полезно на этапе проектирования систем управления. Выберем следующие условия для терминальной задачи идеального релейного управления: –x¢¢+x¢×x2+x×u(t)=0, x(0)= По условиям задачи необходимо определить и точки переключений, и амплитуду реле. Воспользуемся критерием (8) при k=10, значение весового коэффициента было принято равным a=10. Усредненное решение задачи управления по 20 запускам алгоритма
Подводя итоги, отметим, что в работе был рассмотрен специальный подход к решению задачи перевода некоторой динамической системы из заданного состояния в желаемое притом, что исполнительный механизм может работать только в некоторых заранее известных или проектируемых режимах. Подход состоит в переводе задачи управления в задачу поиска оптимума, условного или нет, и в решении полученной оптимизационной задачи. Универсальность предложенного метода позволяет решать задачи в различных постановках, то есть для каждого отдельного семейства задач не требуется новый подход. Предложенный алгоритм, основанный на методе эволюционных стратегий, при нахождении экстремума тестировался на определенном наборе задач управления для различных систем, после чего были определены его наиболее эффективные настройки. Алгоритм разработан таким образом, что поиск происходит одновременно на пространствах с различным типом данных: вещественными и целыми числами, без перевода всех типов данных в бинарную строчку. Таким образом, выполняются все необходимые условия для решаемой задачи. На основании проведенных исследований был реализован и тестирован программный продукт. Представленные в работе примеры решения задач позволяют сделать вывод о том, что с помощью предложенного метода можно не только находить искомое решение задачи терминального управления для управления в виде реле, но и корректировать точки переключения. Дальнейшие исследования направлены на изучение влияния количества точек переключений на эффективность решаемых задач. Литература 1. Aida-zade K.R., Rahimov A.B., Journ. of Autom. and Inform. Sc., 2010, Vol. 42, Iss. 7, pp. 54–64. 2. Кучеров Д.П., Василенко А.В., Иванов Б.П. Алгоритм адаптивного терминального управления динамической системой с элементами дифференцирования // Автоматика. Автоматизация. Электротехнические комплексы и системы. 2009. № 23. C. 166–171. 3. Трушкова Е.А. Синтез управления в окрестности приближенного решения задачи с частично закрепленным правым концом // Программные системы: теория и приложения. 2011, № 2 (6). C. 31–35. 4. Зубер И.Б. Терминальное управление по выходу для нелинейных нестационарных систем // Дифференциальные уравнения и процессы управления. 2004. № 2. C. 36–42. 5. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. М.: Физматлит, 2005. 384 с. 6. Ryzhikov I.S., Semenkin E.S., Proc. Intern. Conf. «ICINCO», 2012, Vol. 1, pp. 333–337. 7. Schwefel H.-P. Evolution and Optimum Seeking: New York, Wiley & Sons., 1995, 456 p. |
| Permanent link: http://swsys.ru/index.php?id=3408&lang=en&page=article |
Print version Full issue in PDF (5.29Mb) Download the cover in PDF (1.21Мб) |
| The article was published in issue no. № 1, 2013 [ pp. 167-171 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Использование алгоритмов оптимизации с самообучением для управления динамически изменяющимися системами
- Проблемы управления конфигурациями в процессе разработки программного обеспечения встроенных систем
- Унифицированное описание функционирования информационных радиоэлектронных систем для оценки программного обеспечения учебно-тренировочных средств
- Информационно-коммуникационная технология комплексного управления деятельностью студентов
- Управление жизненным циклом информатизированных бизнес-процессов
Back to the list of articles
 , (1)
, (1) – вектор-функция своих аргументов; xÎRn – вектор состояний системы;
– вектор-функция своих аргументов; xÎRn – вектор состояний системы;  – кусочно-постоянная функция управления; n – размерность системы, необходимо найти функцию управления u(t), которая переводит систему из известного начального состояния x(0)=x0 в заданное конечное состояние x(T)=x* за конечное время T.
– кусочно-постоянная функция управления; n – размерность системы, необходимо найти функцию управления u(t), которая переводит систему из известного начального состояния x(0)=x0 в заданное конечное состояние x(T)=x* за конечное время T. (2)
(2) – интервалы, порожденные точками переключений, причем
– интервалы, порожденные точками переключений, причем  ,
,  ;
; – множество значений, принимаемых функцией управления; Nu – число значений, которые может принимать функция управления.
– множество значений, принимаемых функцией управления; Nu – число значений, которые может принимать функция управления.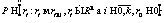 или
или  есть множество точек переключений;
есть множество точек переключений;  – параметр, определяющий количество точек переключений. Множество
– параметр, определяющий количество точек переключений. Множество  является набором индексов, который используется для описания множества интервалов. Каждый интервал Ii,
является набором индексов, который используется для описания множества интервалов. Каждый интервал Ii,  , для функции управления (3) может быть определен уравнением
, для функции управления (3) может быть определен уравнением 
 , в котором
, в котором  – специальная функция.
– специальная функция. , (3)
, (3) – вектор координат системы (1) в конечный момент времени T, функция управления полностью задана множеством
– вектор координат системы (1) в конечный момент времени T, функция управления полностью задана множеством  . Если время нефиксированное, критерий приобретает вид
. Если время нефиксированное, критерий приобретает вид (4)
(4) , (5)
, (5) вместо P появляется еще одно ограничение – rk
вместо P появляется еще одно ограничение – rk и весовой коэффициент a>0. Таким образом, задача условной оптимизации может быть представлена как задача безусловной оптимизации. Прибавляя к обозначенным выше целевым функциям (4) и (5) функцию штрафа, находим целевые функции для задач управления, в которых все точки переключений лежат внутри интервала регулирования:
и весовой коэффициент a>0. Таким образом, задача условной оптимизации может быть представлена как задача безусловной оптимизации. Прибавляя к обозначенным выше целевым функциям (4) и (5) функцию штрафа, находим целевые функции для задач управления, в которых все точки переключений лежат внутри интервала регулирования:  , (6)
, (6) . (7)
. (7) (8)
(8)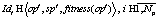 ,
,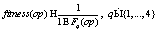 – функция пригодности для задач с функционалами (3), (4), (6), (7) соответственно, или
– функция пригодности для задач с функционалами (3), (4), (6), (7) соответственно, или  – вектор объективных параметров i-го индивида;
– вектор объективных параметров i-го индивида;  – вектор стратегических параметров i-го индивида; Np – объем популяции.
– вектор стратегических параметров i-го индивида; Np – объем популяции. , где для каждого критерия будут использоваться различные множества rj,
, где для каждого критерия будут использоваться различные множества rj,  . Здесь
. Здесь  – множество точек переключения;
– множество точек переключения;  – множество индексов; r3={TÎR} – время управления;
– множество индексов; r3={TÎR} – время управления;  – множество, определяющее Uu. Согласно данному представлению рекомбинация метода эволюционных стратегий может использоваться для множеств r1, r3, r4, а рекомбинация, аналогичная рекомбинации в генетическом алгоритме (одноточечная, двухточечная или равномерная), – для множества r2.
– множество, определяющее Uu. Согласно данному представлению рекомбинация метода эволюционных стратегий может использоваться для множеств r1, r3, r4, а рекомбинация, аналогичная рекомбинации в генетическом алгоритме (одноточечная, двухточечная или равномерная), – для множества r2. – вероятность мутации для каждого гена и Z1 – случайная величина, распределенная по закону Бернулли с
– вероятность мутации для каждого гена и Z1 – случайная величина, распределенная по закону Бернулли с  . Тогда
. Тогда ;
; .
. – вероятность мутации для целочисленного гена; Z2 – случайная величина, распределенная по закону Бернулли с
– вероятность мутации для целочисленного гена; Z2 – случайная величина, распределенная по закону Бернулли с  ; Z3=U(0, 1) – непрерывная случайная величина, распределенная равномерно; Zu – равномерно распределенная дискретная случайная величина, причем
; Z3=U(0, 1) – непрерывная случайная величина, распределенная равномерно; Zu – равномерно распределенная дискретная случайная величина, причем  . Для удобства обозначения используем функцию специального вида,
. Для удобства обозначения используем функцию специального вида, 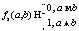 . Каждый ген мутирует, если fz(spi, z3)=1. Таким образом,
. Каждый ген мутирует, если fz(spi, z3)=1. Таким образом,  ,
,  ,
,  , для целочисленных переменных вероятность мутации сохраняется в стратегическом гене.
, для целочисленных переменных вероятность мутации сохраняется в стратегическом гене. , а оператор мутации изменяется:
, а оператор мутации изменяется:  i=1, …, k. В таком случае объективные параметры будут неотрицательными.
i=1, …, k. В таком случае объективные параметры будут неотрицательными. .
.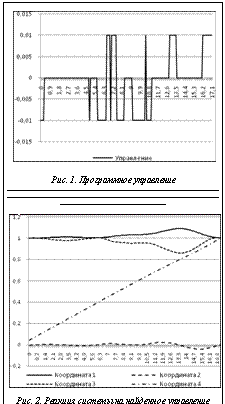 Для данной системы и терминальной задачи управления, когда двигатель может работать в трех режимах, Uu={–0,005, 0, 0,005}, решим задачу с критерием (5), выбрав T=rk, то есть свободное время. После 20 запусков алгоритма было найдено следующее решение: T=17,2, x(17,2)=(1,009, –0,0065, 1,0048, 17,21). Среднее значение целевой функции (5) составило 0,018. В ходе каждого решения целевая функция вычислялась не более 6,25×104 раз. Решение терминальной задачи управления представлено на рисунках 1 и 2.
Для данной системы и терминальной задачи управления, когда двигатель может работать в трех режимах, Uu={–0,005, 0, 0,005}, решим задачу с критерием (5), выбрав T=rk, то есть свободное время. После 20 запусков алгоритма было найдено следующее решение: T=17,2, x(17,2)=(1,009, –0,0065, 1,0048, 17,21). Среднее значение целевой функции (5) составило 0,018. В ходе каждого решения целевая функция вычислялась не более 6,25×104 раз. Решение терминальной задачи управления представлено на рисунках 1 и 2. , x(T)=
, x(T)= , T=5.
, T=5.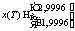 . На рисунке 3 показана реакция системы на найденное управление с рассчитанной амплитудой. Были также рассмотрены аналогичные задачи управления спутником в различных постановках, что позволило сделать вывод об эффективности работы метода.
. На рисунке 3 показана реакция системы на найденное управление с рассчитанной амплитудой. Были также рассмотрены аналогичные задачи управления спутником в различных постановках, что позволило сделать вывод об эффективности работы метода.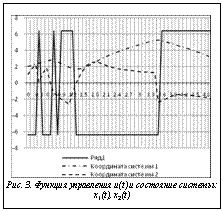 Гибкость алгоритма позволяет решать различные задачи терминального управления, когда исполняющий механизм может работать в виде реле или многоуровневого реле для следующих случаев: со свободным или фиксированным временем, для фиксированных или определяемых значений допустимого множества управления, с фиксированным или нефиксированным числом точек переключений. Важно отметить, что система может быть задана не только в виде дифференциального уравнения, но и алгоритмически.
Гибкость алгоритма позволяет решать различные задачи терминального управления, когда исполняющий механизм может работать в виде реле или многоуровневого реле для следующих случаев: со свободным или фиксированным временем, для фиксированных или определяемых значений допустимого множества управления, с фиксированным или нефиксированным числом точек переключений. Важно отметить, что система может быть задана не только в виде дифференциального уравнения, но и алгоритмически.