Применение нечетких запросов в задачах планирования технического обслуживания и ремонта судов
| Косоуров Д.А. (dkosourov@gmail.com) - НИИ «Центрпрограммсистем» (инженер-программист 2-й категории, аспирант), г. Тверь, Россия | |
| Ключевые слова: ремонт., техническое обслуживание, планирование, нечеткая логика, нечеткие запросы |
|
| Keywords: repair, maintenance service, planning, fuzzy logic, fuzzy queries |
|
|
|
|
Решение задачи прогнозирования изменения важнейших показателей состояния эксплуатируемого объекта или процесса его ремонта позволяет проводить полноценный анализ наиболее вероятной производственной ситуации и принимать соответствующие управленческие решения. При оценке технического состояния судов до последнего времени использовались методы, основанные на физико-техническом и технико-экономическом подходах. Необходимость одновременного учета факторов, имеющих различную природу, а также развитие методов на основе теории нечетких множеств привели к появлению различных подходов, учитывающих наличие дефицита информации. Быстрое развитие и проникновение во все сферы деятельности информационных технологий, использующих большие возможности компьютерной техники, породили информационно-технический подход к решению ряда задач. Информационные технологии расширили возможности прогнозирования, оптимизации и автоматизации процесса эксплуатации и ремонта судов. Отличительной чертой большинства судовых объектов является наличие значительного числа параметров, изменения которых достаточно сложно контролировать, что порождает проблему дефицита информации [1]. Это усложняет процесс прогнозирования состояния данных объектов. Решение этой проблемы необходимо в любой системе, предназначенной для прогнозирования состояния сложных технических объектов и процессов восстановления их работоспособности. Теория нечетких множеств – это расширение классической теории множеств. В классической теории множеств принадлежность элементов некоторому множеству понимается в бинарных терминах в соответствии с четким условием: элемент либо принадлежит, либо не принадлежит данному множеству. В теории нечетких множеств допускается градуированное понимание принадлежности элемента множеству; степень принадлежности элемента описывается при помощи функции принадлежности. Переход от принадлежности элементов заданному множеству к непринадлежности их этому множеству происходит или может происходить постепенно, не резко. Это значение меняется от 0 (полная непринадлежность) до 1 (полная принадлежность). Для реальных сложных систем характерно наличие одновременно разнородной информации [2]: точечных замеров и значений параметров, допустимых интервалов их изменения, статистических законов распределения для отдельных величин, лингвистических критериев и ограничений, полученных от специалистов-экспертов, и т.д. Наличие в сложной многоуровневой иерархической системе управления одновременно различных видов неопределенности делает необходимым использование для принятия решений теории нечетких множеств, которая позволяет адекватно учитывать имеющиеся виды неопределенности. Соответственно и вся информация о режимах функционирования подсистем, областях допустимости и эффективности, целевых функциях, предпочтительности одних режимов работы другим, о риске работы на каждом из режимов для подсистем и т.д. должна быть преобразована к единой форме и представлена в виде функций принадлежности. Такой подход позволяет свести воедино всю имеющуюся неоднородную информацию: детерминированную, статистическую, лингвистическую и интервальную. Эффективность решения проблемы дефицита информации может быть существенно повышена путем объединения подхода, основанного на теории нечетких множеств, с методом экспертных оценок и использования специальных объектно-ориентированных математических моделей. Актуальным является создание алгоритма, эффективно сочетающего в себе перечисленные подходы, что может существенно повысить качество и гибкость процесса прогнозирования. Техническое обслуживание (ТО) и ремонт – это составная часть технической эксплуатации. Суда считаются технически исправными, если удовлетворяют требованиям органов надзора и могут использоваться по прямому назначению с техни- ко-эксплуатационными показателями, предусмотренными технической документацией. Целью функционирования подсистемы «Техническое обслуживание и ремонт» является поддержание и восстановление исправности судов в течение всего срока их службы при минимальных затратах. Эта подсистема включает задачи по оценке технического состояния судов, его контролю, по разработке и внедрению систем технической диагностики, определению структуры ТО и ремонту судов, а также по организации ТО и ремонта [3]. Во всех этих задачах можно использовать теорию нечетких множеств. Как правило, численные характеристики надежности судов и их агрегатов, такие как пробег и износ, являются точными, то есть ответственный за техническое состояние судна принимает решение о ремонте судна, если пробег силового агрегата составил 5 000 км. Использование же теории нечетких множеств позволяет определить необходимость ремонта заранее. Например, силовой агрегат с пробегом в 1 000 км относится к группе нуждающихся в ремонте со степенью 0,1, в 2 000 км – 0,2, в 4 000 – 0,8 и со степенью 1 в случае пробега в 5 000 км. Внедрение нечетких множеств в АСУ ТО и ремонтом позволяет автоматизировать прогнозирование необходимости отказов и ремонта. Теорию нечетких множеств можно использовать и в запросах к реляционным БД. Часто возникает необходимость создать выборку агрегатов, не только нуждающихся в срочном ремонте, но и тех, кому ремонт будет необходим в ближайшее время. Продемонстрируем ограниченность четких запросов на следующем примере. Пусть требуется получить сведения о кораблях не новее 5 лет, у которых пробег составляет более 200 000 км. Данный запрос можно записать на языке SQL следующим образом: SELECT Name FROM SHIPS WHERE (SHIPS.AGE ³ 5 AND SHIPS.MILEAGE > 200 000) Корабль со сроком эксплуатации 4,5 года с пробегом в 198 000 км не попадет в результат запроса, хотя его характеристики почти удовлетворяют требованиям запроса и даже возможно, что полностью попадут в него еще до следующего периода планирования ремонта. Нечеткие запросы помогают справиться с подобными проблемами неполноты информации. Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных. Нечеткая переменная описывается набором (N, X, A), где N – название переменной; X – универсальное множество (область рассуждений); A – нечеткое множество на X. Значениями лингвистической переменной могут быть нечеткие переменные, то есть лингвистическая переменная находится на более высоком уровне, чем нечеткая переменная. Состав каждой лингвистической переменной: – название; – множество своих значений, которое также называется базовым терм-множеством T (элементы базового терм-множества представляют собой названия нечетких переменных); – универсальное множество X; – синтаксическое правило G, по которому генерируются новые термы с применением слов естественного или формального языка; – семантическое правило P, которое каждому значению лингвистической переменной ставит в соответствие нечеткое подмножество множест- ва X. Механизм работы нечетких запросов основан на теории нечетких множеств и ее понятиях, описанных выше. Рассмотрим наиболее распространенные способы генерации новых лингвистических термов на основе базового терм-множества. Это полезно для построения разнообразных семантических конструкций, которые усиливают или ослабляют высказывания, например, «очень высокая цена», «приблизительно среднего возраста» и т.д. Для этого существуют лингвистические модификаторы (linguistic hedges), усиливающие или ослабляющие высказывание. К усиливающим относится модификатор «Очень» (VERY), к ослабляющим – «Более-или-менее» или «Приблизительно», «Почти» (MORE-OR-LESS), нечеткие множества которых описываются функциями принадлежности вида MFVERY(X)=(MF(X))2; MFMORE–OR–LESS(X)= = Для примера формализуем нечеткое понятие «Возраст корабля». Это и будет названием соответствующей лингвистической переменной. Зададим для нее область определения X=[0; 50] и три лингвистических терма: «Малый», «Средний», «Большой». Осталось только построить функции принадлежности для каждого лингвистического терма. Выберем трапецеидальные функции принадлежности со следующими координатами: «Малый»=[0, 5, 10, 15], «Средний»=[12, 15, 20, 30], «Большой»=[25, 35, 40, 50]. В заключение определим операцию нечеткого отрицания (NOT): MF[NOT](X)=1–MF(X). Приведенных выше сведений достаточно для построения и выполнения нечетких запросов. Остановимся на примере. Для простоты предположим, что вся необходимая информация находится в одной таблице со следующими полями: ID – номер корабля, AGE – возраст и MILEAGE – пробег:
Лингвистическая переменная «Возраст» была задана ранее. Определим еще одну лингвистическую переменную для поля MILEAGE с областью определения X=[0; 600 000] и термами «Малый», «Средний» и «Большой» и аналогично построим для них функции принадлежности: «Малый»=[0, 0, 0, 200 000], «Средний»=[90 000, 180 000, 265 000, 330 000], «Большой»=[300 000, 420 000, 600 000, 600 000]. К такой таблице можно делать нечеткие запросы. Например, получить список всех новых кораблей с большим пробегом, что на SQL-подобном синтаксисе запишется так: SELECT * FROM SHIPS WHERE (AGE = «Малый» AND MILEAGE = «Большой») Рассчитав для каждой записи агрегированное значение функции принадлежности MF (при помощи операции нечеткого «И»), получим результат нечеткого запроса:
Записи 1, 2, 5 не попали в результат запроса, так как для них значение функции принадлежности равно нулю. Записей, точно удовлетворяющих поставленному запросу (MF=1), здесь не нашлось. Корабль со сроком эксплуатации 15 лет и с пробегом 398 000 км соответствует запросу с функцией принадлежности 0,82. На практике обычно вводят пороговое значение функции принадлежности, при превышении которого записи включаются в результат нечеткого запроса. Аналогичный четкий запрос можно было бы сформулировать, например, так: SELECT * FROM SHIPS WHERE (AGE£30 AND MILEAGE³420 000) Его результат является пустым. Однако, если мы немного расширим рамки возраста в запросе, рискуем упустить другие корабли с чуть более большим или меньшим возрастом. Поэтому можно сказать, что нечеткие запросы позволяют расширить область поиска в соответствии с изначально заданными человеком ограничениями. Используя нечеткие модификаторы, можно формировать и более сложные запросы: SELECT * FROM SHIPS WHERE (AGE = «Более-или-менее Средний» AND MILEAGE = «Средний») Результат:
Недостатком нечетких запросов является относительная субъективность функций принадлежности. В заключение следует обратить внимание на программные средства, позволяющие реализовать систему нечетких запросов к реляционным БД. В настоящее время активно формируется мировой рынок коммерческих программных продуктов для работы с нечеткой логикой. На нем представлено более 100 пакетов прикладных программ, которые в той или иной мере используют нечеткую логику. Лидерами в данной области являются несколько компаний-разработчиков ПО. Их инструментальные средства ориентированы на применение нечеткой логики в максимальном количестве областей и приложений. Это пакеты CubiCalc (фирма Hyper Logic), FuzzyTECH (Inform Software), FIDE (Ap-tronix), пакеты расширения к MatLab: Fuzzy Logic Toolbox (поставляется с MatLab) и FlexTool for MATLAB (компания Cynap Sys), а также пакет JFS (разработчик Ян Мортенсен) и др. Основным общим недостатком перечисленных программных средств является их довольно высокая стоимость [4]. В статье рассмотрена задача планирования ТО и ремонта судов, приведены примеры применения нечетких запросов к реляционным БД, проанализированы возможности их использования в поставленной задаче. Путем сравнительного противопоставления четких и нечетких запросов ус- тановлено, что для задачи планирования ТО и ремонта судов применение нечетких запросов целесообразно в случаях, когда невозможно сгруппировать данные по четким характеристикам. Примеры, приведенные в статье, показывают, что даже численные значения могут оцениваться неоднозначно. Однако необходимо отметить и недостаток применения нечетких запросов: принадлежность выборки к искомой группе относительно субъективна. Эта субъективная оценка параметров закладывается программистом, поэтому уже с этапа разработки постановки задачи требуется усиленный контроль работы специалистом в области ТО и ремонта судов. Литература 1. Малыхина И.В. Информационное обеспечение процесса прогнозирования при управлении техническим состоянием судовых конструкций на основе аппарата теории нечетких множеств: дис. …канд. техн. наук. СПб: СПб гос. ун-т водн. коммуникаций, 2006. 179 с. 2. Ярушкина Н.Г. Основы теории нечетких и гибридных систем. М.: Финансы и статистика, 2004. 320 с. 3. Пальчик К.Б., Марков С.В. Основы технической эксплуатации флота и судоремонт: Консп. лекц. Новороссийск: МГА им. адм. Ф.Ф. Ушакова, 2008. 82 с. 4. Атанов С.К. Программные средства реализации адаптивных моделей с нечеткой логикой. URL: http://do.gendocs.ru/ docs/index-82232.html (дата обращения: 19.02.2013). |
http://swsys.ru/index.php?id=3454&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Основы структурно-лингвистического подхода в анализе нечетких временных рядов
- Настройка выполнения параллельных программ
- Организация адаптивной маршрутизации данных в электроэнергетических комплексах с использованием онтологических нечетких классификаторов
- Модель выбора мероприятий по обеспечению информационной безопасности на основе нечетких автоматов
- Человекоразумные программные системы интеллектуальной поддержки решений креативных проблем

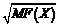 .
.