Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Гибридный нейросетевой алгоритм построения аппроксимационных моделей сложных систем
Аннотация:
Abstract:
| Авторы: Котельников C.A. () - , Усков А.А. (prof.uskov@gmail.com) - Российский университет кооперации, г. Мытищи, Россия, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 17214 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
Как известно, выделяют два основных вида аппроксимационных моделей: параметрические и непараметрические (локально-параметрические). При параметрическом подходе вначале выбирается аппроксимирующая зависимость, известная с точностью до параметров, затем на основе обучающей выборки производится адаптация ее параметров (обучение). К параметрическим методам моделирования относятся: полиномиальные нейронные сети (Σ-Π нейронные сети), многослойные персептроны и др. При непараметрическом подходе вначале так же выбирается тип аппроксимирующей зависимости, но в данном случае по экспериментальным данным строится большое количество указанных зависимостей, каждая из которых действует в некоторой локальной области входных факторов и имеет свои параметры. К непараметрическим методам моделирования относятся: метод М-ближайших узлов, нейронные сети с радиальными базисными элементами и др. В статье предложена гибридная полиномиально-радиальнобазисная нейронная сеть, позволяющая в ряде случаев совместить достоинства параметрического (малая чувствительность к шуму) и непараметрического (отсутствие необходимости подбирать глобальную модель) подходов. Предположим, что исследуемый статический объект имеет n входов (векторный вход
где Функция
где
где Для функций
где
Предположим далее, что на объекте реализован эксперимент, заключающийся в регистрации N пар значений:
При этом В работах академика А.Г. Ивахненко сформулирован принцип адекватности, согласно которому объект и его система моделирования или управления для наиболее оптимального решения задачи должны обладать рядом общих черт. В соответствии с принципом адекватности для решения рассматриваемой задачи предложена гибридная полиномиально-радиальнобазисная искусственная нейронная сеть (HPRBFN, от Hybrid Polynomial Radial Basis Function Network), структурно состоящая из радиально-базисной части (РБЧ), полиномиальной части (ПЧ) и блока взвешенного суммирования. Предложенная искусственная нейронная сеть реализует следующую нелинейную зависимость:
где
Структура нейронной сети определяется числом радиальных нейронов M, числом пи-нейронов L и их параметрами Алгоритм обучения HPRBFN на основе выборки (5) состоит в последовательной реализации трех этапов: 1) обучение РБЧ (параметры Вычислительные эксперименты показали, что если исследуемая зависимость адекватно описывается соотношениями (1) и (2), предложенная гибридная полиномиально-радиальнобазисная нейронная сеть обеспечивает лучшую по точности аппроксимацию по сравнению с другими известными методами. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=346&page=article |
Версия для печати Выпуск в формате PDF (2.31Мб) |
| Статья опубликована в выпуске журнала № 3 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Методы и средства моделирования wormhole сетей передачи данных
- Инструментальные средства управления эффективностью использования инвестиционных ресурсов в процессе реализации проекта
- Адаптивная компиляция на основе данных профилирования
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Нейроподобная сеть для решения задачи оптимизации антенной решетки
Назад, к списку статей



 ) и один выход y. Связь между
) и один выход y. Связь между  и y в n-мерной области
и y в n-мерной области  может быть адекватно представлена моделью:
может быть адекватно представлена моделью: , (1)
, (1) – функция неизвестного вида;
– функция неизвестного вида;  – аддитивная случайная помеха (отражает действие неучитываемых факторов) с нулевым математическим ожиданием и неизвестным распределением на
– аддитивная случайная помеха (отражает действие неучитываемых факторов) с нулевым математическим ожиданием и неизвестным распределением на  .
. , (2)
, (2) – полиномиальная функция:
– полиномиальная функция: , (3)
, (3) – постоянные параметры;
– постоянные параметры;  – целый положительный параметр;
– целый положительный параметр;  – целые неотрицательные параметры;
– целые неотрицательные параметры; 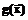 – нелинейная функция общего вида.
– нелинейная функция общего вида. , (4)
, (4) – функционал, возвращающий среднеквадратичное значение функции-аргумента в области
– функционал, возвращающий среднеквадратичное значение функции-аргумента в области  ,
, 
 .
.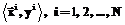 . (5)
. (5) ; значения
; значения  , (6)
, (6) , u – весовые коэффициенты;
, u – весовые коэффициенты;  ,
,  – функции, реализуемые радиальными нейронами и ПЧ сети соответственно:
– функции, реализуемые радиальными нейронами и ПЧ сети соответственно: , (7)
, (7) , (8)
, (8) – евклидова векторная норма;
– евклидова векторная норма;  ,
,  ,
, 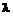 – постоянные параметры;
– постоянные параметры;  – целые неотрицательные параметры.
– целые неотрицательные параметры. ); 2) обучение ПЧ сети (параметры
); 2) обучение ПЧ сети (параметры  ); 3) оптимальная настройка параметра u, определяющего соотношение между влиянием РБЧ и ПЧ на выход сети, по критерию наименьшей погрешности аппроксимации.
); 3) оптимальная настройка параметра u, определяющего соотношение между влиянием РБЧ и ПЧ на выход сети, по критерию наименьшей погрешности аппроксимации.