Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Классификация взаимосвязей в схемах данных
Аннотация:
Abstract:
| Автор: Юмагужин Н.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 12649 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
Во многих коммерческих, государственных и научных организациях распространена ситуация, когда отдельные информационные системы работают на разных программных платформах и используют разные локальные справочники, никак не связанные между собой. Это ставит перед разработчиками программных продуктов ряд задач, связанных с интеграцией данных: ведение централизованных справочников, конвертация и синхронизация данных и др. Первым шагом в решении подобных задач является сопоставление схем данных, которое проводится разработчиками совместно с экспертами в предметной области. На сегодняшний день есть средства, которые автоматически предлагают соответствия между схемами на основе их синтаксического анализа (см.: E. Rahm, P.A. Bernstein. A survey of Approaches to Automatic Schema Matching. VLDB Journal. 10(4):334-350, 2001) либо на основе семантических данных, задаваемых экспертами (см.: S. Spaccapietra, C. Parent. View Integration: A Step Forward in Solving Structural Conflicts. TKDE. 6(2):258-274. 1994). Однако применение этих средств не дает ответа на вопрос о гарантированной возможности решения той или иной задачи интеграции данных. В случае определения соответствий на основе семантических данных от экспертов обычно требуется абстрактное высокоуровневое проектирование: детальное описание объектной модели предметной области либо определение формальной онтологии разрешения конфликтов (см.: S. Ram, J. Park. Semantic Conflict Resolution Ontology (SCROL): An Ontology for Detecting and Resolving Data and Schema-Level Semantic Conflict, TKDE. 16(2). 189-202, 2004). Подход, описанный в данной статье, напротив, не требует от экспертов ничего, кроме указания конкретных взаимосвязей между атрибутами. Рассмотрим задачу сопоставления информации из двух схем данных, содержащих одни и те же физические сущности. При этом допускается, что схемы имеют различные системы кодирования, то есть один и тот же объект может иметь в этих схемах различные идентификаторы. Допускается, что названия таблиц, атрибутов и распределение атрибутов по таблицам могут различаться. Но предполагается, что между схемами существуют взаимосвязи, которые могут быть заданы экспертами. Нашей задачей будет классифицировать типы возможных взаимосвязей и найти необходимые условия для решения различных задач интеграции данных на основе этих взаимосвязей. Пусть некоторая сущность описывается в первой схеме данных отношением A, содержащим кортежи Классификация взаимосвязей доменов 1. Смысловая взаимосвязь доменов. Наиболее общим типом взаимосвязи можно считать случай, когда мы хотя бы можем определить, совпадают ли объекты по атрибутам x и y или не совпадают. Другими словами, задана функция смысловой эквивалентности: 2. Существует конвертирующее отображение из X в Y, если для любого значения
3. Существует обобщающее отображение из X в Y (Y – обобщение X), если для любого значения
4. Существует обобщающее отображение X на Y (X – детализация Y), если для любого значения 5. Изоморфизм доменов, если существуют отображение Кроме приведенных типов взаимосвязей, рассмотрим следующие. 2¢. Существует конвертирующее отображение из Y в X. 3¢. Существует обобщающее отображение из Y в X. 4¢. Существует обобщающее отображение Y на X. Нетрудно доказать следующие свойства приведенной классификации. · Классы взаимосвязей, определяемые условиями 1-5, 2¢-4¢, не совпадают между собой. · Каждое условие с меньшим номером следует из условия с большим номером (в отдельности для условий без штрихов и со штрихами). · Из условия 4 следует 2¢, а из 4¢ следует 2. · Если условия 3 и 3¢ выполняются одновременно, то выполняется условие 5. Классификация взаимосвязей схем данных Будем считать, что объект, заданный кортежем
для всех
такие что Замечание. Для задачи устранения дублирования можно рассматривать не бинарную функцию P, а отображение на отрезок.
В прикладных задачах к этой формуле могут добавляться весовые коэффициенты или использоваться более специфические формулы. Например, если мы решаем задачу сопоставления списков юридических лиц и у нас заданы функции смысловой взаимосвязи:
Обозначение. Множество пар индексов Перейдем к классификации взаимосвязей между схемами данных. 1. Соответствие объектов. Если Select From Where 2. По кортежу из A можно определить кортеж в B. Если существует потенциальный ключ Такой способ проверки применяется при решении задачи переноса данных из одной системы в другую, чтобы избежать возникновения дубликатов. Но для переноса данных необходимы еще два дополнительных условия: 1) переменная-отношение B должна быть обновляемой (либо это должна быть таблица); 2) для всех атрибутов 3. По кортежу из A можно однозначно определить кортеж в B. Если существует потенциальный ключ Теорема. Если в B существует потенциальный ключ K, такой что для всех Пример. Проиллюстрируем действие теоремы задачей сопоставления юридических лиц. Предположим, что во второй из интегрируемых систем реализовано устранение дублирования, не допускающее в переменной-отношении B двух кортежей с одинаковым значением ИНН в атрибуте 4. Отношения A и B синхронизируемы. Если по кортежу из A можно однозначно определить кортеж в B и по кортежу из B можно однозначно определить кортеж в A, будем говорить, что отношения A и B синхронизируемы. Смысл этого условия в том, что если перенести некоторый кортеж a из A в B, а потом обратно, то гарантировано не будет создано новой записи a¢, дублирующей a. Этот факт следует из предыдущей теоремы. Действительно, если по кортежу из B можно однозначно определить кортеж в A, то первичный ключ кортежа b может входить в таблицу соответствия не более одного раза и, следовательно, не может соответствовать кортежам a и a¢ одновременно. Замечание. Не требуется, чтобы потенциальные ключи A и B лежали в В данной статье построена классификация взаимосвязей между доменами и между схемами данных. На основе построенной классификации найдены необходимые условия для решения различных задач интеграции данных: выполнение запросов, получающих информацию из обеих схем данных, перенос (конвертация) данных из одной схемы в другую, cинхронизация данных. В качестве возможного продолжения работы остается поиск достаточных условий для перечисленных задач и дальнейшее изучение свойств построенной классификации. Автор благодарит своего руководителя чл.-корр. РАН, д.ф.-м.н. С.М. Абрамова за постановку задачи и полезные обсуждения. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=347&page=article |
Версия для печати Выпуск в формате PDF (2.31Мб) |
| Статья опубликована в выпуске журнала № 3 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Инструментальные средства управления эффективностью использования инвестиционных ресурсов в процессе реализации проекта
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Информационно-вычислительный комплекс по применению мембран в биотехнологии
- Основные характеристики методики АДЕСА-2 для разработки информационных систем и возможности ее практического применения
- Метод интегрированного описания топологических отношений в геоинформационных системах
Назад, к списку статей



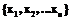 , а во второй схеме данных отношением B, содержащим кортежи
, а во второй схеме данных отношением B, содержащим кортежи  . Отношения A и B могут быть как отдельными таблицами в реляционной схеме данных, так и переменными-отношениями. Запишем формально условие, что A и B содержат одни и те же физические сущности. Будем считать, что в этом случае существуют взаимосвязи между отдельными атрибутами
. Отношения A и B могут быть как отдельными таблицами в реляционной схеме данных, так и переменными-отношениями. Запишем формально условие, что A и B содержат одни и те же физические сущности. Будем считать, что в этом случае существуют взаимосвязи между отдельными атрибутами 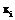 и
и 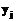 . Рассмотрим различные типы таких взаимосвязей между двумя скалярными атрибутами x и y, определенными на конечных доменах X и Y соответственно.
. Рассмотрим различные типы таких взаимосвязей между двумя скалярными атрибутами x и y, определенными на конечных доменах X и Y соответственно. .
.  , если по атрибутам x и y объекты совпадают,
, если по атрибутам x и y объекты совпадают, 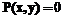 в противном случае.
в противном случае.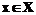 существует значение
существует значение  , такое что по атрибутам x и y объекты будут совпадать. Другими словами, существует отображение
, такое что по атрибутам x и y объекты будут совпадать. Другими словами, существует отображение такое, что для всех
такое, что для всех 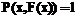 . (1)
. (1)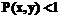 для всех
для всех  . (2)
. (2)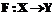 , такое что для всех
, такое что для всех 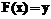 ; и для всех
; и для всех 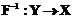 , также удовлетворяющее условиям (1) и (2).
, также удовлетворяющее условиям (1) и (2). в одной схеме данных, совпадает с объектом, заданным кортежем b=
в одной схеме данных, совпадает с объектом, заданным кортежем b= 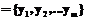 в другой схеме данных, если они совпадают по всем взаимосвязанным атрибутам, то есть для всех функций смысловой взаимосвязи
в другой схеме данных, если они совпадают по всем взаимосвязанным атрибутам, то есть для всех функций смысловой взаимосвязи 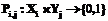 верно равенство
верно равенство  . Множество пар индексов
. Множество пар индексов 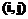 , для которых заданы функции
, для которых заданы функции 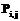 , обозначим
, обозначим  . Тогда можно задать функцию соответствия объектов
. Тогда можно задать функцию соответствия объектов  следующим образом:
следующим образом: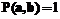 , если
, если ; (3)
; (3) , если существует
, если существует  . (4)
. (4)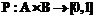 . В этом случае P задается некоторой формулой от функций
. В этом случае P задается некоторой формулой от функций  .
.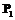 – совпадение ИНН,
– совпадение ИНН, 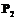 – похожесть наименования,
– похожесть наименования,  – совпадение даты регистрации. Условие, что
– совпадение даты регистрации. Условие, что  дает нам полную уверенность, что юридические лица совпадают, а условия
дает нам полную уверенность, что юридические лица совпадают, а условия 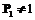 , чтобы определить степень похожести. В этом случае функцию P можно задать следующим образом:
, чтобы определить степень похожести. В этом случае функцию P можно задать следующим образом: .
.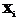 в
в 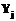 ), обозначим
), обозначим 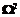 . Для третьего типа –
. Для третьего типа – 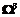 . Для типа 2¢ – обозначим
. Для типа 2¢ – обозначим 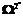 и так далее для всех типов взаимосвязей между доменами. Множество индексов i, входящих в одно из этих множеств
и так далее для всех типов взаимосвязей между доменами. Множество индексов i, входящих в одно из этих множеств 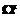 , обозначим
, обозначим  , множество индексов j обозначим
, множество индексов j обозначим 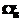 .
.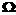 не пусто, и задана функция
не пусто, и задана функция  и
и 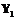 являются первичными ключами отношений A и B. Тогда, если выбрать все пары
являются первичными ключами отношений A и B. Тогда, если выбрать все пары  , для которых
, для которых 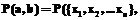
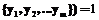 , получим таблицу соответствия N с заголовком
, получим таблицу соответствия N с заголовком 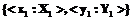 . Имея такую таблицу, можно делать запросы, получающие данные из обеих схем, следующим образом:
. Имея такую таблицу, можно делать запросы, получающие данные из обеих схем, следующим образом: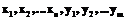

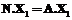 and
and 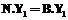
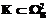 , будем говорить, что по кортежу из отношения A можно определить кортеж в отношении B. Условие
, будем говорить, что по кортежу из отношения A можно определить кортеж в отношении B. Условие  , для всех
, для всех 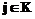 . Используя эти отображения, можно по кортежу
. Используя эти отображения, можно по кортежу 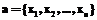 построить набор атрибутов
построить набор атрибутов 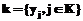 . И поскольку K – это потенциальный ключ, в отношении B может существовать не более одного кортежа b, содержащего атрибуты k. Таким образом, можно по кортежу a из отношения A быстро найти в отношении B кортеж b такой, что
. И поскольку K – это потенциальный ключ, в отношении B может существовать не более одного кортежа b, содержащего атрибуты k. Таким образом, можно по кортежу a из отношения A быстро найти в отношении B кортеж b такой, что 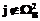 , должны быть заданы значения по умолчанию или выполнена автоматическая нумерация.
, должны быть заданы значения по умолчанию или выполнена автоматическая нумерация. , будем говорить, что по кортежу из отношения A можно однозначно определить кортеж в отношении B. Смысл этого условия раскрывает следующая теорема.
, будем говорить, что по кортежу из отношения A можно однозначно определить кортеж в отношении B. Смысл этого условия раскрывает следующая теорема.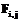 из
из  входит в таблицу соответствия N не более одного раза.
входит в таблицу соответствия N не более одного раза.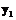 , то есть
, то есть 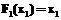 оставляет ИНН без изменений. Тогда, применяя теорему, можно заключить, что если построить таблицу соответствия, то каждая запись из переменной-отношения A будет входить в нее не более одного раза.
оставляет ИНН без изменений. Тогда, применяя теорему, можно заключить, что если построить таблицу соответствия, то каждая запись из переменной-отношения A будет входить в нее не более одного раза. . Для того чтобы A и B были синхронизируемы, достаточно, чтобы потенциальный ключ A лежал в
. Для того чтобы A и B были синхронизируемы, достаточно, чтобы потенциальный ключ A лежал в  , а потенциальный ключ B лежал в
, а потенциальный ключ B лежал в  .
.