Важнейшей задачей промышленного производства является поддержание безаварийной работы различного рода машин и агрегатов. Это приводит к необходимости их технической диагностики без нарушения и останова технологического процесса. Одним из важнейших методов такой диагностики является спектральный анализ колебательных процессов. На практике в качестве модели этих процессов, как правило, рассматривают аддитивную смесь гармонических компонент и статистически независимого по отношению к ним широкополосного шума e(t) [1, 2], то есть
 ,
,
где ak и bk – коэффициенты гармонического ряда Фурье; f0 – основная частота; K – общее число гармонических компонент.
Соотношение для x(t) в полярных координатах будет иметь вид
 ,
,
где каждой k-й гармонике с частотой fk=kf0 соответствуют амплитуда ak и начальная фаза jk:
 k=1, 2, …, K.
k=1, 2, …, K.

 Спектральный анализ колебательного процесса связан с вычислением на дискретных частотах fk=kf0 оценок амплитудного ak и фазового jk спектров на фоне широкополосного шума e(t), имеющего непрерывный спектр. Получившие широкое распространение классические цифровые методы вычисления спектральных оценок, как правило, требуют выполнения прямого преобразования Фурье многоразрядных отсчетов наблюдаемой реализации колебательного процесса, что приводит к значительным затратам времени даже при выполнении быстрого преобразования Фурье [3].
Спектральный анализ колебательного процесса связан с вычислением на дискретных частотах fk=kf0 оценок амплитудного ak и фазового jk спектров на фоне широкополосного шума e(t), имеющего непрерывный спектр. Получившие широкое распространение классические цифровые методы вычисления спектральных оценок, как правило, требуют выполнения прямого преобразования Фурье многоразрядных отсчетов наблюдаемой реализации колебательного процесса, что приводит к значительным затратам времени даже при выполнении быстрого преобразования Фурье [3].
В [4] показано, что повысить быстродействие цифровых процедур вычисления оценок амплитудного спектра ak позволяет знаковое аналого-стохастическое квантование  где
где  – центрированная (то есть с нулевым математическим ожиданием) реализация колебательного процесса; x (t) – равномерно распределенный в пределах от –Xmax до +Xmax вспомогательный сигнал (Xmax – наиболее вероятное максимально возможное по абсолютной величине значение, которое может принять
– центрированная (то есть с нулевым математическим ожиданием) реализация колебательного процесса; x (t) – равномерно распределенный в пределах от –Xmax до +Xmax вспомогательный сигнал (Xmax – наиболее вероятное максимально возможное по абсолютной величине значение, которое может принять  ); sgn{…} – символ знаковой функции, которая может принимать значения –1 или +1 в зависимости от знака значения ее аргумента.
); sgn{…} – символ знаковой функции, которая может принимать значения –1 или +1 в зависимости от знака значения ее аргумента.
В [5] на основе данного вида квантования разработаны цифровые алгоритмы вычисления оценок коэффициентов Фурье ak и bk, которые в дальнейшем используются для вычисления оценок амплитудного ak и фазового jk спектров. Согласно этим алгоритмам имеем следующие оценки коэффициентов Фурье:
 ,
,
k=1, 2, 3, …, K;
 k=1, 2, 3, …, K, где T – продолжительность времени анализа; Xmax – наиболее вероятное максимально возможное по абсолютной величине значение, которое может принять колебательный процесс; z(t0) – результат знакового аналого-стохастического квантования в начальный момент времени анализа;
k=1, 2, 3, …, K, где T – продолжительность времени анализа; Xmax – наиболее вероятное максимально возможное по абсолютной величине значение, которое может принять колебательный процесс; z(t0) – результат знакового аналого-стохастического квантования в начальный момент времени анализа;  и p – отсчеты времени и их количество, соответствующие смене знака результата знакового аналого-стохастического квантования в пределах интервала времени анализа.
и p – отсчеты времени и их количество, соответствующие смене знака результата знакового аналого-стохастического квантования в пределах интервала времени анализа.
 Вычисление оценок
Вычисление оценок  и
и  коэффициентов Фурье с помощью приведенных алгоритмов не требует выполнения многоразрядных цифровых операций умножения, что ведет к увеличению быстродействия анализа колебательных процессов. Данные алгоритмы послужили основой создания специализированной измерительной системы (ИС) для цифрового спектрального анализа колебательных процессов. В ходе ее создания для обеспечения широких функциональных возможностей и удовлетворения требованиям, предъявляемым к современным ИС, особое внимание было уделено системной организации вычислительных процессов и логике их выполнения. В результате разработано комплексное ПО, которое выполняет процедуры вычисления оценок амплитудного спектра и реализует логические операции, предусмотренные алгоритмами подготовки исходных данных к их обработке и процессом спектрального анализа, а также осуществляет управление работой ИС в целом и формирует выходные данные. При этом было учтено требование конструктивной и функциональной однородности программных модулей.
коэффициентов Фурье с помощью приведенных алгоритмов не требует выполнения многоразрядных цифровых операций умножения, что ведет к увеличению быстродействия анализа колебательных процессов. Данные алгоритмы послужили основой создания специализированной измерительной системы (ИС) для цифрового спектрального анализа колебательных процессов. В ходе ее создания для обеспечения широких функциональных возможностей и удовлетворения требованиям, предъявляемым к современным ИС, особое внимание было уделено системной организации вычислительных процессов и логике их выполнения. В результате разработано комплексное ПО, которое выполняет процедуры вычисления оценок амплитудного спектра и реализует логические операции, предусмотренные алгоритмами подготовки исходных данных к их обработке и процессом спектрального анализа, а также осуществляет управление работой ИС в целом и формирует выходные данные. При этом было учтено требование конструктивной и функциональной однородности программных модулей.
Разработка ИС велась с учетом принципов
– использования объектно-ориентированного анализа для определения, представления, проектирования и документирования ПО систем;
– установления связей между структурными элементами ИС, которые обеспечивают ее целостность;
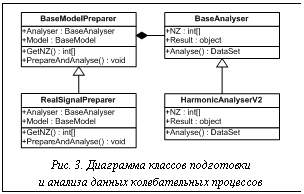
– На втором уровне 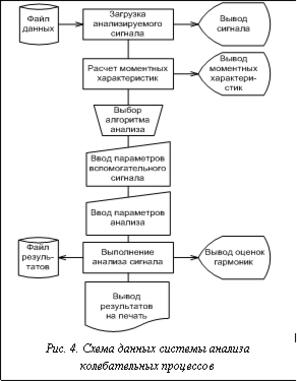 определяется организация хранения данных колебательного процесса, которая реализуется в классе RealSignalModelBase, являющемся наследником класса BaseModel. В этом классе атрибут PointsCountToRead определяет максимальное количество отсчетов данных колебательного процесса для загрузки в ИС. Атрибут PointsCount показывает, какое количество данных было загружено. Атрибут Points является массивом для хранения значений отсчетов времени.
определяется организация хранения данных колебательного процесса, которая реализуется в классе RealSignalModelBase, являющемся наследником класса BaseModel. В этом классе атрибут PointsCountToRead определяет максимальное количество отсчетов данных колебательного процесса для загрузки в ИС. Атрибут PointsCount показывает, какое количество данных было загружено. Атрибут Points является массивом для хранения значений отсчетов времени.
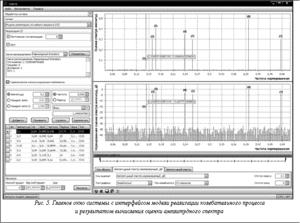
В процессе эксперимента параметры гармонических компонент (значения частот и амплитуд) подбирались таким образом, чтобы получаемые спектры имели ряд особенностей, по которым можно судить об эффективности работы ИС. В частности, модель реализации колебательного процесса представляла собой смесь семи гармонических компонент и равномерно распределенного белого шума с нулевым математическим ожиданием и единичной дисперсией. В итоге анализа данной модели были получены оценки амплитудного спектра. Данные оценки отражены на верхнем графике рисунка 5. Для наглядности на нижнем графике этого рисунка приведены нормированные значения данной оценки в децибелах. Спектральные линии четко разрешимы по частоте, и сильные гармонические компоненты не маскируют слабые. Следует обратить внимание на то, что даже при высоком уровне шума (дисперсия равна единице) гармоническая компонента с амплитудой 0,1 ясно различима на фоне шума. Из нижнего графика видно, что шум подавлен минимум на 30 дБ по сравнению с основными гармоническими компонентами анализируемой реализации колебательного процесса.
 Подводя итоги, следует отметить, что разработана специализированная ИС, ПО которой выполнено на основе парадигмы объектно-ориентированного программирования, что позволяет расширять набор функциональных модулей для подготовки и проведения спектрального анализа данных. Программная организация ИС на основе алгоритмов вычисления оценок амплитудного спектра с использованием знакового аналого-стохастического квантования исследуемых колебательных процессов обеспечивает оперативность проведения технической диагностики.
Подводя итоги, следует отметить, что разработана специализированная ИС, ПО которой выполнено на основе парадигмы объектно-ориентированного программирования, что позволяет расширять набор функциональных модулей для подготовки и проведения спектрального анализа данных. Программная организация ИС на основе алгоритмов вычисления оценок амплитудного спектра с использованием знакового аналого-стохастического квантования исследуемых колебательных процессов обеспечивает оперативность проведения технической диагностики.
Литература
1. Васильев Ю.Н., Бесклетный М.Е., Игумцев Е.А. Вибрационный контроль технического состояния газотурбинных, газоперекачивающих агрегатов. М.: Недра, 1987. 197 с.
2. Tsypin B.V., Myasnikova M.G., Kozlov V.V., Ionov S.V., Application of methods of digital spectral estimation in the measurement of the parameters of a signal, Measurement Techniques, 2011, Vol. 53, no. 10, pp. 1118–1124.
3. Marple S.L.J., Digital Spectral Analysis with Applications. Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1987, 492 p.
4. Якимов В.Н. Математическое представление потоков дискретного знакового преобразования непрерывных сигналов // Вестн. Самар. гос. техн. ун-та. 2000. Вып. 8. С. 190–192. (Технические науки).
5. Yakimov V.N., Digital harmonic analysis of multicomponent random processes, Measurement Techniques, Publisher: Springer, NY, 2006, Vol. 49, no. 4, pp. 341–347.
6. Fowler M., Rice D., Foemmel M., Hieatt E., Mee R., Stafford R., Patterns Of Enterprise Application Architecture, Addison Wesley, 2002, 560 p.
References
1. Vasilev Yu.N., Beskletny M.E., Igumtsev E.A., Vibratsionny kontrol tekhnicheskogo sostoyaniya gazoturbinnykh, gazoperekachivayushchikh agregatov [Diagnosis vibration control of gas turbine units and gas-compressor units], Moscow, Nedra, 1987, 197 p.
2. Tsypin B.V., Myasnikova M.G., Kozlov V.V., Ionov S.V., Measurement Techniques, 2011, Vol. 53, no. 10, pp. 1118 –1124.
3. Marple S.L.J., Digital Spectral Analysis with Applications, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1987, 492 p.
4. Yakimov V.N., Vestnik Samarskogo gos. tekhnich. univ., Tekhnich. nauki [Proc. Samara State Technical Univ., Technics], Samara, 2000, iss. 8, pp. 190–192.
5. Yakimov V.N., Measurement Techniques, Springer, NY, 2006, Vol. 49, no. 4, pp. 341–347.
6. Fowler M., Rice D., Foemmel M., Hieatt E., Mee R., Sta f-ford R., Patterns Of Enterprise Application Architecture, Addison Wesley, 2002, 560 p.



 ,
, ,
,
 k=1, 2, …, K.
k=1, 2, …, K.

 где
где  – центрированная (то есть с нулевым математическим ожиданием) реализация колебательного процесса; x (t) – равномерно распределенный в пределах от –Xmax до +Xmax вспомогательный сигнал (Xmax – наиболее вероятное максимально возможное по абсолютной величине значение, которое может принять
– центрированная (то есть с нулевым математическим ожиданием) реализация колебательного процесса; x (t) – равномерно распределенный в пределах от –Xmax до +Xmax вспомогательный сигнал (Xmax – наиболее вероятное максимально возможное по абсолютной величине значение, которое может принять  ,
, k=1, 2, 3, …, K, где T – продолжительность времени анализа; Xmax – наиболее вероятное максимально возможное по абсолютной величине значение, которое может принять колебательный процесс; z(t0) – результат знакового аналого-стохастического квантования в начальный момент времени анализа;
k=1, 2, 3, …, K, где T – продолжительность времени анализа; Xmax – наиболее вероятное максимально возможное по абсолютной величине значение, которое может принять колебательный процесс; z(t0) – результат знакового аналого-стохастического квантования в начальный момент времени анализа;  и p – отсчеты времени и их количество, соответствующие смене знака результата знакового аналого-стохастического квантования в пределах интервала времени анализа.
и p – отсчеты времени и их количество, соответствующие смене знака результата знакового аналого-стохастического квантования в пределах интервала времени анализа. Вычисление оценок
Вычисление оценок  и
и  коэффициентов Фурье с помощью приведенных алгоритмов не требует выполнения многоразрядных цифровых операций умножения, что ведет к увеличению быстродействия анализа колебательных процессов. Данные алгоритмы послужили основой создания специализированной измерительной системы (ИС) для цифрового спектрального анализа колебательных процессов. В ходе ее создания для обеспечения широких функциональных возможностей и удовлетворения требованиям, предъявляемым к современным ИС, особое внимание было уделено системной организации вычислительных процессов и логике их выполнения. В результате разработано комплексное ПО, которое выполняет процедуры вычисления оценок амплитудного спектра и реализует логические операции, предусмотренные алгоритмами подготовки исходных данных к их обработке и процессом спектрального анализа, а также осуществляет управление работой ИС в целом и формирует выходные данные. При этом было учтено требование конструктивной и функциональной однородности программных модулей.
коэффициентов Фурье с помощью приведенных алгоритмов не требует выполнения многоразрядных цифровых операций умножения, что ведет к увеличению быстродействия анализа колебательных процессов. Данные алгоритмы послужили основой создания специализированной измерительной системы (ИС) для цифрового спектрального анализа колебательных процессов. В ходе ее создания для обеспечения широких функциональных возможностей и удовлетворения требованиям, предъявляемым к современным ИС, особое внимание было уделено системной организации вычислительных процессов и логике их выполнения. В результате разработано комплексное ПО, которое выполняет процедуры вычисления оценок амплитудного спектра и реализует логические операции, предусмотренные алгоритмами подготовки исходных данных к их обработке и процессом спектрального анализа, а также осуществляет управление работой ИС в целом и формирует выходные данные. При этом было учтено требование конструктивной и функциональной однородности программных модулей.

