Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Моделирование системы управления запасами
Аннотация:
Abstract:
| Автор: Литвинов Н.Н. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15540 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
Совершенствование методов управления запасами сырья и определения объемов заказываемой партии позволяет снизить складские издержки, уменьшить объемы продукции, не удовлетворяющие текущим потребностям покупателей. При математической формализации процессов управления запасами очень часто приходится использовать скачкообразные, недифференцируемые и кусочно-непрерывные функции. Как правило, это обусловливается необходимостью учета эффектов концентрации, фиксированных затрат и платы за заказ. В связи с этим получаемые задачи с трудом поддаются аналитическому решению классическими методами, однако могут быть успешно решены с помощью аппарата динамического программирования. Рассмотрим достаточно типичную задачу, возникающую в процессе планирования деятельности системы снабжения. Пусть имеется некоторая система снабжения (склад, оптовая база и т.п.), планирующая свою работу на n периодов. Ее деятельность сводится к обеспечению спроса конечных потребителей на некоторый продукт, для чего она осуществляет заказы производителю этого продукта. Спрос конечных потребителей в данной модели рассматривается как некоторая интегрированная величина, принимающая заданные значения для каждого из периодов, и он должен всегда удовлетворяться. Также предполагается, что заказ, посылаемый производителю, удовлетворяется им полностью и временем между заказом и его выполнением можно пренебречь. Введем обозначения: yk – остаток запаса после (k–1)-го периода; dk – заранее известный суммарный спрос в k-м периоде; xk – заказ (поставка от производителя) в k-м периоде; ck(xk) – затраты на выполнение заказа объема xk в k-м периоде; sk(xk) – затраты на хранение запаса объема xk в k-м периоде. После получения поставки и удовлетворения спроса объем товара, подлежащего хранению в период k, составит
Расходы на получение и хранение товара в период k описываются функцией
Естественной в рамках сформулированной модели представляется задача нахождения последовательности оптимальных управлений (заказов)
При решении поставленной задачи методом динамического программирования в качестве функции состояния управляемой системы
поскольку yk=x -xk+dk>0 , и
Система рекуррентных соотношений (4)–(5) позволяет найти последовательность функций состояния
Особый интерес представляет частный случай задачи (1)–(2), при котором предполагается, что функции затрат на пополнение запаса ck(xk) являются вогнутыми по xk, a функции затрат на хранение sk(xk) являются линейными относительно объема хранимого запаса, то есть Обозначим функцию затрат в течение k-го периода через
или В силу сделанных предположений все функции затрат fk(xk, yk+l) являются вогнутыми (как суммы вогнутой и линейной функций). Данное свойство значительно упрощает процесс решения, так как для поиска минимума вогнутых функций fk(xk, yk+l) достаточно рассмотреть только две крайние точки множества, на котором отыскивается минимум. С учетом введенного обозначения задачу (1)–(2) можно записать в виде:
при условиях
Рассмотрим процедуру решения (9)–(10). Так как ищется минимум суммы вогнутых функций fk(xk, yk+l), то решение будет достигаться на одной из крайних точек множества, определяемого условиями (10). Общее число переменных xk и yk в системе (10) равно 2 n. Однако, учитывая то, что в ней только n уравнений, в оптимальном плане будет не более n ненулевых компонент, причем для каждого периода k значения xk и yk не могут равняться нулю одновременно (в силу необходимости удовлетворения спроса либо за счет заказа, либо за счет запаса). Формально это утверждение можно представить в виде условия дополняющей нежесткости:
где С точки зрения содержательной интерпретации условия (10)–(11) означают, что при оптимальном управлении заказ поставщику на новую партию не должен поступать, если в начале периода имеется ненулевой запас, или размер заказа должен равняться величине спроса за целое число периодов. Отсюда следует, что запас на конец последнего периода должен равняться нулю: yn+1=0. Последнее позволяет решать задачу в прямом направлении, применяя рекуррентное соотношение:
где Учитывая (11)–(12) и вогнутость fk(xk,x), заключаем, что минимум (13) достигается в одной из крайних точек xk = 0 или xk=x + dk, поэтому
тогда для предыдущего периода функция состояния может быть выражена как
на основе чего в общем виде получаем модифицированную форму для рекуррентного соотношения:
При дальнейших конкретизирующих предположениях о виде функций fk(xk, уk+1) можно получить еще более компактные формы для рекуррентных соотношений. Однако эти вопросы носят достаточно частный характер, и их рассматривать в данном случае нецелесообразно. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=349&page=article |
Версия для печати Выпуск в формате PDF (2.31Мб) |
| Статья опубликована в выпуске журнала № 3 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Инженерная программа трехмерного моделирования магнитных систем LittleMag
- Разработка корпоративной базы в области химии и химической технологии
- Унифицированный информационный интерфейс и его реализация в комплексной САПР
- Моделирование процесса остывания отливок в литейной форме
- К вопросу параметризации свойств программных средств обучения
Назад, к списку статей



 . Учитывая смысл параметра yk, можно записать соотношение:
. Учитывая смысл параметра yk, можно записать соотношение: . (1)
. (1)
 . Планом задачи можно считать вектор х = (х1, х2, ..., хn), компонентами которого являются последовательные заказы в течение рассматриваемого промежутка времени. Соотношение между запасами (1) в сочетании с некоторым начальным условием связывает состояния системы с выбранным планом и позволяет выразить суммарные расходы за все n периодов функционирования управляемой системы снабжения в форме аддитивной целевой функции:
. Планом задачи можно считать вектор х = (х1, х2, ..., хn), компонентами которого являются последовательные заказы в течение рассматриваемого промежутка времени. Соотношение между запасами (1) в сочетании с некоторым начальным условием связывает состояния системы с выбранным планом и позволяет выразить суммарные расходы за все n периодов функционирования управляемой системы снабжения в форме аддитивной целевой функции: . (2)
. (2) и связанных с ними оптимальных состояний (запасов)
и связанных с ними оптимальных состояний (запасов)  , которые обращают в минимум (2). В качестве начального условия используем требование о сохранении после завершения управления заданного количества товара уп+1, а именно:
, которые обращают в минимум (2). В качестве начального условия используем требование о сохранении после завершения управления заданного количества товара уп+1, а именно: . (3)
. (3) логично взять минимальный объем затрат, возникающих за первые k периодов при условии, что в k-й период имеется запас
логично взять минимальный объем затрат, возникающих за первые k периодов при условии, что в k-й период имеется запас  . Тогда можно записать основное рекуррентное соотношение:
. Тогда можно записать основное рекуррентное соотношение: (4)
(4) . (5)
. (5)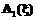 ,
, ,…,
,…,  и условных оптимальных управлений
и условных оптимальных управлений  ,
,  ,…,
,…,  . На n-м шаге с помощью начального условия (3) можно определить
. На n-м шаге с помощью начального условия (3) можно определить  . Остальные значения оптимальных управлений
. Остальные значения оптимальных управлений 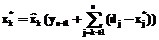 . (6)
. (6)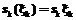 . Параллельно заметим, что обе предпосылки являются достаточно реалистичными.
. Параллельно заметим, что обе предпосылки являются достаточно реалистичными. , (7)
, (7) . (8)
. (8) (9)
(9) . (10)
. (10) , (11)
, (11)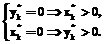 (12)
(12) , (13)
, (13)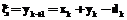 .
. , (14)
, (14) (15)
(15)
 (16)
(16)