Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Ортогональное кодирование и его использование с фазоразностной модуляцией
Аннотация:
Abstract:
| Авторы: Рабин А.В. () - , Мирончиков Е.Т. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 19445 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
При обработке сигналов на приемной стороне системы передачи информации различают первичные и вторичные виды обработки. Под первичным видом обработки понимается принятие решения о значении передаваемого символа и иногда об оценке условной вероятности ошибки. Под вторичным – исправление ошибок в декодирующем устройстве с использованием жестких решений или полученных ранее условных вероятностей ошибки (см.: Johannesson Rolf, Zigangirov Kamil Sh. Fundamentals of convolutional coding. – IEEE Press, 1999). Целью разделения на виды обработки является уменьшение сложности и, как следствие, стоимости приемной аппаратуры. В тех случаях, когда надежность связи должна быть особенно высокой, оба вида обработки выполняются одновременно. Такой способ приема называется приемом в целом. В работе показано, что между первым и вторым видами обработки можно ввести еще один вид, который не ограничивает возможности указанных ранее видов обработки, а позволяет без внесения избыточности дополнительно снизить вероятность ошибки. Уменьшение вероятности ошибки осуществляется за счет использования ортогонального кодирования, которое является аналогом сверточного кодирования над полем действительных чисел. Основная цель этой работы заключается в исследовании характеристик систем передачи информации с ортогональным кодированием и фазоразностной модуляцией (ФРМ). Ортогональное кодирование осуществляется умножением входного информационного вектора на квадратную полиномиальную матрицу, элементами которой являются полиномы от переменной D с целыми коэффициентами. Будем называть ее системной матрицей и обозначать как G(D). На приемной стороне декодирование осуществляется умножением на обратную системную матрицу. Обозначим ее как
где I − единичная матрица. Множитель При использовании ортогонального кодирования совместно с фазовой модуляцией целесообразно ограничиться применением матрицы Рассмотрим следующий метод синтеза системной и обратной системной матриц. Вначале выбираем обратную системную матрицу В работе матрица В качестве примера рассмотрим ортогональное кодирование OC4 с обратной системной матрицей
и соответствующей ей системной матрицей
При умножении матриц получим:
Рассмотрим применение ортогонального кодирования в системах с ФРМ. Оценим уменьшение результирующей вероятности ошибки за счет использования ортогонального кодирования. Изложение проведем на конкретном примере передачи двоичных сигналов По системной матрице
Декодирующая матрица H для данного примера имеет вид
Каждый столбец декодирующей матрицы ортогонален всем строкам кодирующей матрицы, кроме одной. По этой причине операция декодирования каждой группы из четырех символов сводится к вычислению скалярных произведений части принятого сообщения и столбцов декодирующей матрицы на каждом шаге декодирования. Действительно, произведение кодирующей и декодирующей матриц для данного примера имеет вид
Из (5) видно, что уровень входного сигнала в данном случае увеличивается в двенадцать раз, а из алгоритма декодирования ясно, что дисперсия шума возрастает в восемь раз при предположении, что в канале действует белый гауссовский шум. Таким образом, имеется некоторый выигрыш в отношении сигнал/шум, так как рассматриваемое ортогональное кодирование не вносит дополнительную избыточность. Отметим, что ортогональные коды состоят из последовательностей целых чисел с разными знаками. Поэтому возникает необходимость в согласовании кодовых символов и методов модуляции. В рассматриваемом примере для реализации ортогонального кодирования приходится использовать фазовую модуляцию с высокой кратностью. Из матрицы G следует, что в рассматриваемом примере возможное число сдвигов фаз равно 45.
Рассмотрим пример конечного сообщения. Пусть оно содержит восемь символов и имеет вид Тогда кодовое слово, подаваемое на модулятор, представляется следующим вектором:
Из вида кодирующей матрицы следует, что возможные значения фаз на выходе модулятора есть Последовательность сигналов с такими фазами передается по каналу. На приемной стороне оцениваются фазы принятых колебаний, и по их значениям определяется принятый вектор, компоненты которого при отсутствии шума в канале принимают значения из множества
Далее, умножая на декодирующую матрицу, получим оценки передаваемых символов, которые принимают значения
Решения о значениях передаваемых двоичных символов принимаем на основании сравнения с нулевым порогом. На рисунке BDPSK − это график зависимости вероятности ошибки от отношения сигнал/шум в канале с двоичной ФРМ (подробнее см.: Ю.Б. Окунев. Теория фазоразностной модуляции. М. 1979). Остальные графики получены в результате моделирования и показывают зависимости вероятности ошибки от отношения сигнал/шум для OC4, OC8, OC16, OC32 и фазоразностной модуляции. Для каждого случая выбиралась обратная системная матрица глубины, равной половине порядка матрицы. Предлагаемые ортогональные коды для формирования кодового слова используют двоичные входные сигналы. Картина не меняется, если эти двоичные символы образуют кодовое слово какого-либо кода с исправлением ошибок. Таким образом, ортогональное кодирование можно рассматривать как кодирование, относящееся к непрерывному каналу, а корректирующие коды как кодирование, относящееся к дискретному каналу. Совместное использование ортогональных и корректирующих кодов повышает помехоустойчивость системы передачи намного больше, чем использование только корректирующих кодов. На основании изложенного можно сделать следующие выводы. Техническая реализация ортогонального кодирования достаточно проста. На каждом шаге процесс декодирования сводится к вычислению нескольких скалярных произведений и сравнению с фиксированным порогом. Параметры системных и обратных системных матриц обеспечивают дополнительный выигрыш в отношении сигнал/шум. Этот выигрыш получен за счет более эффективного использования энергии передаваемых сигналов. Ортогональное кодирование не вносит дополнительную избыточность в системы передачи. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=355&page=article |
Версия для печати Выпуск в формате PDF (2.31Мб) |
| Статья опубликована в выпуске журнала № 3 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Оптимизация структуры базы данных информационной системы ПАТЕНТ
- Комплекс автоматизированного проектирования геотехнических сооружений "КАППА"
- Место XML-технологий в среде современных информационных технологий
- Функционально-информационные модели бухгалтерского учета
- Компьютерные технологии сегодня: тенденции и прогнозы
Назад, к списку статей



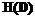 . Требуется, чтобы эти матрицы удовлетворяли условию
. Требуется, чтобы эти матрицы удовлетворяли условию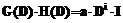 , (1)
, (1)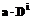 показывает, что задержка в получении символов на приемной стороне составляет i тактов, а амплитуда входного сигнала увеличивается в a раз.
показывает, что задержка в получении символов на приемной стороне составляет i тактов, а амплитуда входного сигнала увеличивается в a раз.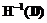 . Системная матрица
. Системная матрица 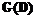 получается умножением матрицы
получается умножением матрицы 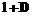 . Это четное число назовем глубиной матрицы (см.: О.А. Сергеев, Е.Т Мирончиков. Система обмена информацией с кодовым разделением каналов. Образование и бизнес: российская практика и зарубежный опыт. СПб. 2001). Остальным элементам на главной диагонали присвоим значения единицы. Вне главной диагонали элементы принимают следующие значения: элементы нечетных строк справа и нечетных столбцов вниз от главной диагонали равны
. Это четное число назовем глубиной матрицы (см.: О.А. Сергеев, Е.Т Мирончиков. Система обмена информацией с кодовым разделением каналов. Образование и бизнес: российская практика и зарубежный опыт. СПб. 2001). Остальным элементам на главной диагонали присвоим значения единицы. Вне главной диагонали элементы принимают следующие значения: элементы нечетных строк справа и нечетных столбцов вниз от главной диагонали равны  , элементы четных строк справа и четных столбцов вниз от главной диагонали равны
, элементы четных строк справа и четных столбцов вниз от главной диагонали равны  (2)
(2)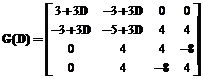 . (3)
. (3)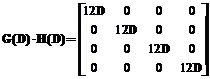 . (4)
. (4)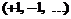 . Для простоты будем предполагать, что вторичная обработка (исправление ошибок корректирующими кодами) при передаче двоичных сигналов не рассматривается. Системы передачи с двоичной фазоразностной модуляцией и системы с ортогональным кодированием и ФРМ сравниваются по вероятности ошибки на выходе канала. Применение ортогонального кодирования приводит к увеличению кратности модуляции.
. Для простоты будем предполагать, что вторичная обработка (исправление ошибок корректирующими кодами) при передаче двоичных сигналов не рассматривается. Системы передачи с двоичной фазоразностной модуляцией и системы с ортогональным кодированием и ФРМ сравниваются по вероятности ошибки на выходе канала. Применение ортогонального кодирования приводит к увеличению кратности модуляции. .
.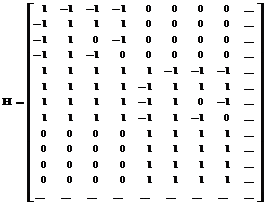 .
.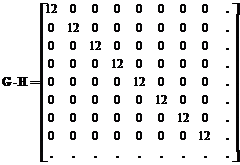 . (5)
. (5)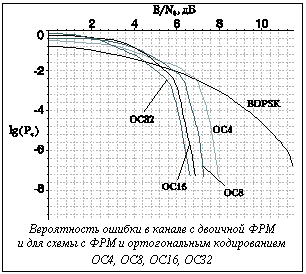 Система передачи работает следующим образом. Операция кодирования представляет собой перемножение информационной последовательности из
Система передачи работает следующим образом. Операция кодирования представляет собой перемножение информационной последовательности из 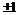 и кодирующей матрицы. В результате получаем кодовое слово, каждый символ которого принимает значение из множества
и кодирующей матрицы. В результате получаем кодовое слово, каждый символ которого принимает значение из множества 
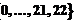 . Эта последовательность поступает на модулятор, в котором реализуется ФРМ порядка 45. На приемной стороне оценивается величина сдвига фаз между соседними символами принятого сообщения. На выходе демодулятора получаем также последовательность чисел из того же множества
. Эта последовательность поступает на модулятор, в котором реализуется ФРМ порядка 45. На приемной стороне оценивается величина сдвига фаз между соседними символами принятого сообщения. На выходе демодулятора получаем также последовательность чисел из того же множества 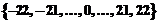 . Далее декодер на каждом шаге вычисляет скалярное произведение полученной последовательности и декодирующей матрицы. В результате получим оценки передаваемых символов, которые при отсутствии шума должны иметь значения
. Далее декодер на каждом шаге вычисляет скалярное произведение полученной последовательности и декодирующей матрицы. В результате получим оценки передаваемых символов, которые при отсутствии шума должны иметь значения 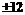 . Решения о передаваемых символах принимаем на основании сравнения с нулевым порогом.
. Решения о передаваемых символах принимаем на основании сравнения с нулевым порогом. .
.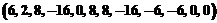 .
. ,
,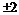 ,¼,
,¼,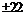 , умноженные на
, умноженные на 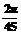 . В модуляторе в соответствии с принятым кодовым словом получается следующая последовательность фаз:
. В модуляторе в соответствии с принятым кодовым словом получается следующая последовательность фаз: 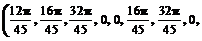
 .
.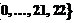 :
: .
.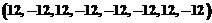 .
.