Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Минимизация рисков при разработке программных средств
Аннотация:Рассматриваются проблемы, с которыми сталкиваются команды, разрабатывающие программные средства по методологии Scrum, а также влияние на качество программных средств неразрешение этих проблем. Предложены метрики, позволяющие количественно оценивать риски несвоевременного выполнения работ, связанные с простоем отдельных членов команды и неоптимальной декомпозицией запланированных работ на задачи. Предлагается метод, ориентированный на минимизацию рисков, которые связаны с неэффективной занятостью членов Scrum-команды в процессе итерации. Представлены алгоритмы для применения предложенного метода на этапах планирования и выполнения работ процесса разработки, организованного в соответствии с методологией Scrum.
Abstract:The article examines the obstacles that are usual for software development teams working with the Scrum methodology and the impact on software quality. The authors propose a method aimed at risks minimizing when risks are connected with ineffective productivity time of Scrum-team members during Scrum iteration. The paper suggests the meas-ures that help in the risks quantitative assessment for late performances when the risks are linked with team members’ idle time and non-optimal decomposition of scheduled work.
| Авторы: Бахтизин В.В. ( bww@bsuir.by) - Белорусский государственный университет информатикии радиоэлектроники, г. Минск, Беларусь, кандидат технических наук, Кузиков А.А. (zander@me.by) - Белорусский государственный университет информатикии радиоэлектроники (аспирант ), г. Минск, Беларусь | |
| Ключевые слова: гибкое управление проектами., минимизация рисков, качество программных средств, гибкая методология разработки |
|
| Keywords: agile project management, risks minimizing, software quality, agile software development |
|
| Количество просмотров: 7631 |
Версия для печати Выпуск в формате PDF (13.63Мб) Скачать обложку в формате PDF (1.39Мб) |
Многие компании сегодня рассматривают возможность перехода к инкрементной и эволюционной моделям процесса разработки программных средств (ПС), так как каскадная модель процесса разработки ПС имеет ряд недостатков [1, 2]. Более того, применение гибких методологий обусловлено необходимостью выпуска качественных ПС раньше конкурентов. Гибкие методологии раз- работки ПС, детализирующие и расширяющие инкрементную модель, а также хорошо зарекомендовавшие себя в условиях меняющихся требований, адаптированы и достаточно широко применяются в реальных проектах. Среди многообразия существующих гибких методологий одно из лидирующих мест занимает методология Scrum, которая, предоставляя каркас организации и управления процессом разработки ПС, успешно сочетается с методологиями, ориентированными на различные инженерные практики [3, 4], например, экстремальное программирование и разработку, управляемую тестами. Методология Scrum благодаря своей относительной простоте и адаптируемости широко используется компаниями, предоставляющими услуги по разработке и тестированию ПС. Как правило, Scrum-команда выполняет разработку ПС по требованиям заказчика, представленным в журнале требований к продукту в виде историй, в течение итераций продолжительностью от двух до шести недель [3–5]. Фиксированные временные рамки обусловливают выполнение только полезных и важных заказчику требований и выпуск работоспособных версий ПС на регулярной основе. Кроме того, декомпозиция требований на отдельные задачи всячески стимулирует членов команды к сотрудничеству, постоянному отслеживанию зависимости своих задач от результатов работы других членов. Тем не менее Scrum-команды нередко сталкиваются с проблемами невыполнения работ, запланированных в рамках итерации, вследствие изменения цели итерации, вызванного непредвиденной сменой приоритетов пользовательских требований, и срыва графиков выполнения запланированных работ [5]. Как правило, риски, связанные с изменением цели итерации, предусмотреть сложно. Однако оценить риски невыполнения запланированных работ в рамках итерации и управлять ими вполне возможно. Проблема срыва графиков выполнения работ в течение итерации Согласно методологии Scrum, истории, выбранные для реализации в рамках итерации, можно рассматривать как достаточно независимые участки работы. Однако между задачами, на которые декомпозирована каждая история, как правило, существуют взаимосвязи, определяющие порядок их выполнения членами Scrum-команды. Пренебрежение данными взаимосвязями зачастую приводит к тому, что отдельные члены команды получают возможность приступить к выполнению назначенных им задач ближе к концу итерации. Подобные ситуации нередко имеют место в группах специалистов по обеспечению качества и технических писателей, когда результаты работы группы разработчиков невозможно протестировать или задокументировать за оставшееся до конца итерации время. Как правило, к концу итерации при невыполнении нормативов времени по реализации отдельной истории Scrum-команда поставлена перед следующим выбором: – получить отказ в приемке истории от владельца продукта и переместить ее в журнал продукта для доработки в рамках одной из последующих итераций; – получить одобрение в приемке истории от владельца продукта, сократив затраты времени на оставшиеся в рамках истории задачи, например, путем исключения задач, не выполнимых в рамках текущей итерации, либо уменьшения объемов работ по ним; – получить одобрение в приемке истории от владельца продукта, составив и передав ему список известных проблем, разрешение которых планируется в следующих итерациях. Каждый из этих вариантов приводит к снижению качества разрабатываемого ПС ввиду негативного влияния, оказываемого на ряд характеристик. Расширение временных рамок итерации либо уточнение скорости работы Scrum-команды может способствовать выполнению работ в срок, однако не разрешает проблему неэффективной занятости ресурсов. В данной работе описывается метод, призванный оценить организацию работ команды над историями в рамках итерации, управлять порядком выполнения работ и предложить алгоритмы по снижению рисков несвоевременной реализации требований заказчика. Термины и определения Определение 1. Множество членов Scrum-команды можно описать следующим образом: Определение 2. Объем работ для реализации в рамках итерации можно представить в виде следующего множества историй, каждая из которых, например, отражает требование к разрабатываемому ПС или является описанием обнаруженного в ПС дефекта: Определение 3. Задача – независимый участок работы, выполнение которой можно поручить отдельному члену команды. Каждую историю sk можно декомпозировать на следующее множество задач: Поскольку k-я история декомпозирована на задачи таким образом, что каждая задача может быть выполнена только одним членом команды, то каждой задаче wk,i истории sk можно поставить в соответствие исполнителя, роль которого играет член Scrum-команды. Определение 4. Множество исполнителей задач k-й истории можно описать следующим образом: Каждый член команды ml может быть неоднократно задействован в выполнении различных задач истории sk, то есть играть роль исполнителя одной и более задач k-й истории, либо не иметь назначенных задач, что выражается следующим отображением: Assgn:Ak®M. (1) В общем случае имеет значение последовательность выполнения задач, так как существует зависимость между ними. Поскольку множество задач Wk составляет декомпозицию истории sk, но k-я история считается выполненной только после приемки у владельца истории (обычно владельца продукта), можно полагать, что некоторая конечная задача wk,0, представляющая собой работы по приемке истории sk, будет зависеть от выполнения всего множества задач k-й истории. Исполнителем задачи wk,0, как правило, является лицо, выполняющее приемку истории, например владелец продукта ak,0. Следовательно, с учетом конечной задачи wk,0 множеству задач WkÈ{wk,0} истории sk будет соответствовать множество исполнителей AkÈ{ak,0}. Определение 5. Ориентированный граф Gk=(Vk, Ek) является представлением истории sk, если множество его вершин Vk=WkÈ{wk,0} есть множество задач истории sk. Элементами множества Ek являются упорядоченные пары задач вида (wk,i, wk,j), i¹j, причем задача wk,j зависит от выполнения задачи wk,i. Определение 6. Множество W¢k называется множеством начальных задач, если выполнение таких задач не зависит от выполнения каких-либо других задач k-й истории, то есть
Применительно к каждой задаче wk,i k-й истории будем полагать, что задача обладает свойством атомарности (неделимости) в такой мере, что задача wk,i может быть назначена только одному исполнителю ak,i, а переход от выполнения задачи wk,i к выполнению одной из зависимых от нее задач wk,j, например, при (wk,i, wk,j)ÎEk и indeg(wk,j)=1, возможен только при условии завершения исполнителем ak,i работ над задачей wk,i. Свойство атомарности задачи исключает наличие в орграфе Gk петель и циклов, четко определяя изменение объема работ Scrum-команды над конкретной историей. Поскольку в случае методологии Scrum объем работ для каждого члена команды выражается в единицах времени (часах, днях), количество времени, требующееся исполнителю для завершения задачи, будет отражать риски, связанные с несвоевременным выполнением запланированных работ. Подобным показателем служит временная функция t(wk,i, ak,i, t), определяемая отображением t:Vk× (AkÈ{ak,0}) ×(R+È{0})®R+È{0}, (2) где Vk – множество задач k-й истории; (AkÈ{ak,0}) – множество исполнителей, имеющих назначения в k-й истории; R+ – множество положительных действительных чисел. Функция (2) отражает время, необходимое исполнителю ak,i для непосредственного выполнения работ над задачей wk,i на момент времени t от начала итерации. Как правило, для хорошо оцененных исполнителем задач функцию t можно рассматривать как невозрастающую и неотрицательную в течение итерации. Оценка времени выполнения работ членом команды Для каждой задачи wk,i следует проанализировать множество Wk на наличие зависимостей. Подобный анализ содействует построению очередности выполнения задач. Определение 7. Dk,i – это такое подмножество задач истории sk, что начало работ над задачей Dk,i ={wk,j ÷"jÎ[1, Nk], j¹i, (wk,j, wk,i)ÎEk}. (3) Из определения 6 и формулы (3) следует, что для любой начальной задачи wk,iÎW¢k Dk,i=Æ. Негативное влияние на выполнение планов итерации в фиксированные временные рамки оказывает неэффективное использование рабочего времени членами Scrum-команды в результате незапланированных простоев. Рассмотрим время, необходимое исполнителю ak,i для завершения всех работ над задачей wk,i. Очевидно, что данная величина слагается из времени непосредственного выполнения исполнителем ak,i работ над задачей wk,i, а также времени ожидания завершения работ над множеством задач Dk,i на момент времени t от начала итерации: TC(wk,i, ak,i, t)=t(wk,i, ak,i, t)+Tw(wk,i, ak,i, t). (4) Время ожидания Tw(wk,i, ak,i, t) исполнителем ak,i начала работ над задачей wk,i можно определить как максимальное время, необходимое для завершения работ над задачами Dk,i. Следует отметить, что две задачи, wk,i и wk,j, назначенные разным членам Scrum-команды (Assgn(ak,i)¹Assgn(ak,j)), предполагают возможность их одновременного выполнения, если не существует ориентированного пути между wk,i и wk,j и все задачи из множеств Dk,i и Dk,j выполнены. Таким образом, если отображение (2) инъективно, то есть в истории sk для каждого члена команды ml имеется не более одной назначенной ему на исполнение задачи wk,i, то на момент времени t от начала итерации время ожидания начала выполнения задачи wk,i исполнителем ak,i, таким, что Assgn(ak,i)=ml, можно задать формулой
Если в истории sk для некоторого члена команды ml имеется более одной назначенной ему на исполнение задачи, например wk,i и wk,j, возможность одновременного выполнения таких задач исключается. При отсутствии ориентированного пути между wk,i и wk,j необходимо задать отношение зависимости между задачами. Для учета данной специфики необходимо преобразовать граф Gk в соответствии с приведенным далее алгоритмом. После преобразования графа Gk время ожидания начала выполнения некоторой задачи wk,i исполнителем ak,i на момент времени t от начала итерации также рассчитывается по формуле (5). Алгоритм преобразования графа истории Алгоритм, преобразующий граф k-й истории из множества S историй, запланированных для реализации в течение итерации, состоит из следующих шагов. Вход: орграф истории sk. 1. Выбрать очередного члена команды ml из множества M членов Scrum-команды. 2. Выбрать подмножество задач Qk,l:={wk,i÷ iÎ[0, Nk]}ÍVk, для исполнителей которых выполняется условие Assgn(ak,i)=ml. 3. Если для члена команды ml в k-й истории имеется более одной назначенной ему для исполнения задачи, то есть ½Qk,l½>1, перейти к шагу 4. Иначе перейти к шагу 11. 4. Выбрать очередную задачу wk,i из множества Qk,l. Для определенности будем полагать, что просмотр множества задач Qk,l для выбора очередной задачи организован в соответствии с увеличением индекса задачи 5. Из множества задач Qk,l выбрать очередную задачу wk,j, для которой выполняется условие i 6. Если в графе Gk существует ориентированный путь через вершины wk,i и wk,j, перейти к шагу 5. Иначе перейти к шагу 7. 7. Расширить множество дуг Ek графа Gk за счет новой дуги (wk,i, wk,j) и рассчитать значение Tw1:=TW(wk,0, ak,0, t). 8. Заменить дугу (wk,i, wk,j) дугой (wk,j, wk,i) в множестве дуг Ek графа Gk и рассчитать значение Tw2:= Tw(wk,0, ak,0, t). 9. Если Tw1 10. Заменить дугу (wk,j, wk,i) дугой (wk,i, wk,j) во множестве дуг Ek графа Gk и перейти к шагу 5. 11. Если рассмотрено все множество M членов команды, завершить алгоритм. Иначе перейти к шагу 1. Выход: орграф истории sk, в котором для задач, принадлежащих каждому непустому множеству Dk,i, есть возможность их одновременного выполнения соответствующими исполнителями. Минимальное время простоя члена команды Функция (5) характеризует потенциальную величину времени простоя члена Scrum-команды, назначенного исполнителем ak,i задачи wk,i. Очевидно, что эффективная последовательность выполнения задач имеет место, если функция (5) принимает минимальное значение для члена команды ml в рамках всех K историй на момент времени t от начала итерации, что, учитывая (1) и (5), можно записать следующим образом:
Рассчитанное по формуле (6) значение TW* позволяет определить историю и незавершенную задачу, на выполнении которой следует сосредоточиться участнику ml Scrum-команды. Потенциальная выполнимость истории Рассмотрим функцию TC(wk,0, ak,0, t), значение которой соответствует времени, необходимому для завершения работ над k-й историей на момент времени t от начала итерации. То есть значение функции TC(wk,0, ak,0, 0) отражает фактическую трудоемкость истории на момент начала итерации. Определение 8. Потенциальная выполнимость k-й истории характеризуется величиной
где wk,0 – конечная задача k-й истории; ak,0 – исполнитель конечной задачи wk,0; TI – время, характеризующее продолжительность итерации, в рамках которой запланирована история sk; tÎ[0, TI) – время, прошедшее от начала итерации. Значение функции (7) позволяет определить, можно ли теоретически завершить выполнение работ в рамках заданной истории за время, оставшееся до завершения итерации. История sk потенциально выполнима в рамках итерации, если rk(t)Î[0,1]. Иначе, если rk(t)<0, существует риск невыполнения k-й истории за время, оставшееся до завершения итерации. На практике, если для истории sk справедливо rk(0)=0, существует риск невыполнения задач истории за время, ограниченное рамками итерации. Поэтому на этапе планирования работ рекомендуется применять критерий rk(0)Î(0,1] для определения факта потенциальной выполнимости k-й истории. Применение метода минимизации рисков при планировании работ в рамках итерации С целью минимизации рисков, связанных с неэффективной занятостью членов команды в течение итерации, на этапе планирования итерации необходимо придерживаться следующего алгоритма. 1. Отсортировать множество S историй, запланированных для реализации в течение итерации, по убыванию степени их важности. 2. Выбрать очередную историю sk из множества S историй, запланированных для реализации в течение итерации. Если рассмотрены все истории из множества S, перейти к шагу 15. Иначе перейти к шагу 3. 3. Если история sk не декомпозирована на задачи (Vk=Æ), перейти к шагу 4. Иначе перейти к шагу 5. 4. Декомпозировать историю на задачи 5. Выбрать задачу wk,i из множества задач Vk. Если рассмотрены все задачи истории sk, перейти к шагу 10. Иначе перейти к шагу 6. 6. Определить множество задач Dk,i, от выполнения которых зависит задача wk,i, основываясь на предварительной информации о задаче. 7. Если задаче wk,i не назначен исполнитель из числа членов Scrum-команды, перейти к шагу 8. Иначе перейти к шагу 9. 8. Назначить исполнителя задачи wk,i (Assgn(ak,i):=ml). 9. Задать время непосредственного выполнения работ над задачей wk,i на момент начала итерации (t(wk,i, ak,i, 0)) и перейти к шагу 5. 10. Применить к истории sk алгоритм преобразования графа Gk. После проведенных преобразований графа истории множество задач Dk,i для каждой задачи wk,i k-й истории будет уточнено. 11. Рассчитать значение rk0:= rk(0) с целью определения факта выполнимости истории sk в рамках итерации на момент ее начала. 12. Если для истории sk выполняется rk0Î[0,1], перейти к шагу 2. Иначе перейти к шагу 13. 13. Декомпозировать историю sk на подмножество историй U с меньшим числом задач. 14. Исключить историю sk из множества S историй, дополнить множество S историй подмножеством U: S:=S\{sk}ÈU и перейти к шагу 2. 15. Выбрать очередного члена команды ml из множества M членов Scrum-команды. 16. Рассчитать значение минимального времени простоя члена команды ml на момент начала итерации: Twl*:=TW*(ml, 0). 17. Осуществить выбор членом команды ml задачи wk,i, для которой TW(wk,i, ak,i, 0)=Twl* и Assgn(ak,i)=ml. 18. Если рассмотрено все множество M членов команды, завершить алгоритм. Иначе перейти к шагу 15. Применение метода минимизации рисков при выполнении работ в рамках итерации В соответствии с методологией Scrum предполагается, что на ежедневно проводимых совещаниях каждый член команды отразит изменение объема работ над назначенными ему задачами. Следовательно, ежедневная частота пересчета значений нестационарных функций (4)–(7) является рекомендуемой, например Dt=1 день или Dt=8 часов. С целью минимизации рисков, связанных с неэффективной занятостью членов команды в течение итерации, на этапе работы над историями и задачами итерации продолжительностью TI в момент времени t 1. Выбрать очередную историю sk из множества S историй, запланированных для реализации в течение итерации. Если рассмотрены все истории из множества S, перейти к шагу 7. Иначе перейти к шагу 2. 2. Выбрать задачу wk,i из множества задач Vk. Если рассмотрены все задачи истории sk, перейти к шагу 4. Иначе перейти к шагу 3. 3. Для задачи wk,i и ее исполнителя ak,i обновить значение функции (2) на текущий момент времени t от начала итерации и перейти к шагу 2. 4. Рассчитать значение rkt:=rk(t) с целью определения факта выполнимости истории sk в рамках итерации на момент времени t от начала итерации. 5. Если для истории sk выполняется rktÎ[0, 1], перейти к шагу 1. Иначе перейти к шагу 6. 6. Прекратить работы над задачами истории sk, исключить историю из множества S историй S:=S\{sk}, переместив ее в журнал продукта, и перейти к шагу 1. 7. Выбрать очередного члена команды ml из множества M членов Scrum-команды. 8. Рассчитать время окончания работ TCl:=TC(wk,i, ak,i, t) члена команды ml над соответствующей текущей задачей wk,i (Assgn(ak,i)=ml). 9. Если работы над текущей задачей завершены, то есть TCl=0, перейти к шагу 10. Иначе перейти к шагу 7. 10. Рассчитать значение минимального времени простоя члена команды ml на момент времени t от начала итерации (TWl*:=TW*(ml, t)). 11. Члену команды ml осуществить переход к выполнению следующей назначенной ему задачи wk,i, для которой ($kÎ[1, K], $iÎ[1, Nk]) (Assgn(ak,i)=mlÙTW(wk,i, ak,i, t)=TWl*). 12. Если рассмотрено все множество M членов команды, перейти к шагу 13. Иначе перейти к шагу 7. 13. Если по истечении времени Dt, например, в момент проведения очередного ежедневного совещания, t В заключение отметим, что предложенный в данной работе метод, основанный на формальной оценке трудоемкости работ, позволяет разрешить проблему неэффективной организации работ в Scrum-командах путем корректировки последовательности выполнения работ в течение итерации. На примере двух алгоритмов продемонстрировано применение метода на этапах планирования и выполнения работ процесса разработки, организованного в соответствии с методологией Scrum. Предложены метрики, которые позволяют количественно оценить простой членов команды (6), а также выполнимость (7) запланированных работ в рамках итерации. Применение предложенных алгоритмов при планировании и выполнении работ в рамках Scrum-итерации способствует выполнению всего объема запланированных работ по разработке и тестированию ПС, следовательно, позволяет обеспечить заявленный уровень качества разрабатываемого ПС. Литература 1. Бахтизин В.В., Глухова Л.А. Технология разработки программного обеспечения: учеб. пособие. Минск: БГУИР, 2010. 267 с. 2. Comer E.R., Alternative Software Life Cycle Models, Software Engineering, Piscataway, NJ, IEEE Computer Society Press, 1997, pp. 404–414. 3. Kniberg H., Scrum and XP from the Trenches, C4Media, 2007, 140 p. 4. Schwaber K., The enterprise and scrum, Microsoft Press Redmond, WA, USA, 2007, 176 p. 5. Keith C., Agile game development with Scrum, Addison-Wesley, 2010, 340 p. References 1. Bakhtizin V.V., Glukhova L.A., Tekhnologiya razrabotki programmnogo obespecheniya (Software engineering technology), Minsk, BSUIR, 2010. 2. Comer E.R., Software Engineering, Piscataway, NJ, IEEE Computer Society Press, 1997, pp. 404–414. 3. Kniberg H., Scrum and XP from the Trenches, C4Media, 2007. 4. Schwaber K., The enterprise and scrum, Microsoft Press Redmond, WA, USA, 2007. 5. Keith C., Agile game development with Scrum, Addison-Wesley, 2010. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=3577&page=article |
Версия для печати Выпуск в формате PDF (13.63Мб) Скачать обложку в формате PDF (1.39Мб) |
| Статья опубликована в выпуске журнала № 3 за 2013 год. [ на стр. 151-155 ] |
Назад, к списку статей



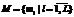 , где ml – l-й член команды; L – количество членов Scrum-команды.
, где ml – l-й член команды; L – количество членов Scrum-команды. , где sk – k-я история итерации; K – число историй, выбранных для реализации в рамках итерации.
, где sk – k-я история итерации; K – число историй, выбранных для реализации в рамках итерации. , где wk,i – i-я задача k-й истории итерации; Nk – число задач в k-й истории.
, где wk,i – i-я задача k-й истории итерации; Nk – число задач в k-й истории. , где ak,i – i-й исполнитель, назначенный на выполнение i-й задачи k-й истории итерации; Nk – число исполнителей задач в k-й истории.
, где ak,i – i-й исполнитель, назначенный на выполнение i-й задачи k-й истории итерации; Nk – число исполнителей задач в k-й истории.
 непосредственно зависит от результатов их выполнения:
непосредственно зависит от результатов их выполнения: . (5)
. (5) . Если для задачи wk,i i=Nk, то перейти к шагу 11. Иначе перейти к шагу 5.
. Если для задачи wk,i i=Nk, то перейти к шагу 11. Иначе перейти к шагу 5. . (6)
. (6) , (7)
, (7) .
.