Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Прототип системы анализа состояния вычислительного кластера на основе метода опорных векторов
Аннотация:С ростом сложности вычислительных кластеров для обеспечения их эффективной работы на первый план выходит проблема отказоустойчивости. Ее решение в настоящее время является одной из самых активно развивающихся областей, связанной с высокопроизводительными вычислениями. В данной работе рассмотрена задача построения автоматизированной системы классификации состояний вычислительного кластера с целью прогнозирования и своевременного выявления нештатных ситуаций в его работе. Для ее решения был предложен алгоритм, использующий методы машинного обучения на основе подхода опорных векторов (SVM/SVR). Отличительной особенностью используемого алгоритма является его модульный характер, допускающий выбор наиболее эффективных методов для решения подзадач всего алгоритма обработки входных данных. На примере анализа данных мониторинга, собранных с реально действующих вычислительных кластеров, была показана принципиальная применимость предложенного алгоритма для обнаружения новых состояний вычислительного кластера: при правильном выборе пара-метров используемых методов удается осуществлять прогнозирование возможных будущих состояний с точностью 6–16 % и фиксировать критическое изменение контролирующих величин в пределах 3–5 шагов прогноза. При малом числе показаний сенсорных датчиков, содержащих выпадающие значения (5–10 %), наблюдается устойчивость системы к сбоям в показаниях сенсорных датчиков. Возможное дальнейшее развитие автоматизированной системы связано с использованием online-алгоритмов SVM/SVR и методов выявления сложных типов аномального поведения вычислительных кластеров.
Abstract:Increasing complexity of computer cluster systems highlights the problem of failure tolerance to provide their efficient work. Nowadays this problem is one of the most dynamically elaborating in the area of high performance computa-tions. The paper considers different implementation aspects of automated system performing classification of computer clus-ter states to predict and check critical events. The algorithm using statistical learning theory approach (support vector meth-od) is proposed to address these subjects. Its modular structure permits to use more robust and efficient methods to deal with subtasks of the general algorithm. The the algorithm implementation prototype is tested on sets of real-world data. Provided that correct parameters are selected its anomaly detection capability is shown. In the test experiments the prediction error of future possible states is 6–16 % while the critical change of control parameters is fixed within 3–5 prognosis time steps. Sen-sor failure tolerance with small numbers (5–10 %) of data series with outliers is proved. Possible improvements of the auto-mated classification system are related with on-line SVR algorithms and methods to deal with more sophisticated anomalous behaviour of computer clusters.
Современный вычислительный кластер (ВК) является технически сложной системой, представляющей собой комплекс взаимосвязанных и взаимодействующих подсистем: вычислительных узлов, сетевого оборудования, инженерной инфраструктуры. Мониторинг состояния всех подобных подсистем требует наличия разветвленной сети сенсорных датчиков, занимающихся сбором информации о разнообразных параметрах системы. В то же время для эффективного управления инфраструктурой ВК необходима такая упрощенная система анализа, которая позволяла бы на основе всей получаемой от сенсорных датчиков информации выявлять наступление нештатной ситуации и оперативно реагировать на нее. Актуальной задачей представляется построение автоматизированной системы анализа, осуществляющей обработку данных мониторинга с использованием современных статистических методов. Разнообразие типов сенсорных датчиков, являющееся следствием разнообразия свойств контролируемых параметров, приводит к разнообразию статистических свойств получаемых от них данных мониторинга, поэтому из всех методов статистической обработки данных наибольшую эффективность при решении данной задачи имеют универсальные, непараметрические методы. К их числу относятся методы машинного обучения. В данной работе описываются принципы построения прототипа реализации алгоритма анализа данных мониторинга (далее обозначаемого как прототип), предназначенного для обнаружения критических ситуаций, возникающих при работе ВК. В качестве базового подхода был выбран подход на основе метода опорных векторов (support vector method / support vector regression – SVM/SVR). В общих чертах он состоит в оценке целевой функции с помощью ее подгонки к набору заданных данных и используется в самой широкой предметной области: от изучения поведения финансового рынка до вычисления возможной загруженности электрических сетей или транспортного потока [1]. Популярность практического применения этого подхода связана с его простотой, универсальностью и эффективностью, особенно при решении задач из реальной жизни, где, как правило, требуется использование нелинейных моделей. Немаловажным является его высокая производительность, позволяющая использовать такой подход в автоматизированных системах, работающих в режиме реального времени. Общая схема алгоритма В предлагаемом подходе анализ данных мониторинга осуществляется путем построения двух статистических моделей и их использования для обработки новых непрерывно поступающих данных в автоматическом режиме. Первая из моделей описывает набор собранных ранее данных мониторинга, соответствующих стабильной работе ВК. Эту модель далее будем называть моделью множества нормальных, типичных состояний ВК. Вторая модель на основе данных, полученных в течение некоторого промежутка времени, непосредственно предшествующего моменту построения модели, позволяет вычислять возможные будущие состояния ВК. Далее будем ссылаться на нее как на модель регрессора. Все параметры моделей задаются пользователем перед запуском всей системы, исходя из статистических свойств обрабатываемых данных. Обе модели строятся автоматически с определенной периодичностью с учетом поступления новых данных. Например, типичное время между двумя последовательными построениями модели нормальных состояний ВК может составлять 24 часа, тогда как модель регрессора может обновляться раз в минуту. Общая схема обработки данных заключается в периодическом применении модели множества нормальных состояний для решения задачи классификации возможных будущих состояний ВК, получаемых с использованием модели регрессора. Представление данных. Наиболее простой подход в описании состояния ВК в каждый момент времени заключается в представлении его в виде случайного вектора: S(t)=(s1(t), s2(t), ..., sN(t))ÎÂN, где si(t) – показания сенсоров системы мониторинга (СМ) в момент времени t (i=1, …, N), N –число сенсоров, осуществляющих мониторинг вычислительного комплекса. При таком представлении данных мониторинга задача их анализа может быть сформулирована как анализ статистических свойств многомерного временного ряда. При этом следует отметить, что, поскольку отдельные компоненты такого динамически меняющегося многомерного вектора представляют собой величины разной физической природы, для их совместного рассмотрения необходимо провести масштабирование каждой компоненты в отдельности. Наибольшее распространение получил способ масштабирования:
Здесь В данной работе при построении моделей и при дальнейшей обработке все показания сенсорных датчиков приводятся к стандартному виду z-score, однако для удобства пользователя результаты обработки выводятся в первоначальном масштабе. Регуляризация входных данных. При обработке данных мониторинга по представленному алгоритму возникают две проблемы, связанные с возможностью построения в каждый момент времени вектора состояний ВК, которые необходимо решить до начала процедуры обработки, то есть построения моделей множества нормальных состояний и модели регрессора. Во-первых, нерегулярное и асинхронное поступление показаний от разных сенсорных датчиков мешает построению вектора S(t), а во-вторых, ошибочные показания датчиков могут оказать существенное влияние на результаты обработки. Во многих системах мониторинга для решения проблемы регулярности поступления данных мониторинга проводится процедура интерполяции значений (как правило, это линейная кусочно-непрерывная интерполяция) таким образом, чтобы измерения были доступны через одинаковые интервалы времени, – данный подход, например, по умолчанию применяется в популярном средстве хранения данных RRDB [2]. В таком случае возможны исчезновение, сглаживание «пиковых» значений измерений после регуляризации, что может быть в некоторых ситуациях нежелательным. Наряду с проблемой регуляризации временного шага входных данных существует проблема возможности появления так называемых вы- падающих значений, под которыми принято понимать значения переменных, которые существенным образом искажающие статистические характеристики данных. Одномерные выпадающие значения, как правило, характеризуются экстремальными значениями, однако существуют и более сложные ситуации [3], которые требуют специальных методов для их выявления. В данной работе рассматривается только самый простой вариант аномального поведения одномерных данных, когда за выпадающие значения принимаются те, которые имеют большую абсолютную величину после приведения к стандартному масштабу z-score. Как правило, это величины с z-score по модулю ³3,29. Однако z-score сильно зависит от размера выборки N. С учетом вышеизложенного регуляризация входных данных мониторинга в рассматриваемом прототипе осуществляется в несколько шагов по следующей схеме. 1. Удаление выпадающих значений, то есть данных, распознанных как аномальные в предыдущие моменты времени; удаление данных, не обновлявшихся в течение определенного промежутка времени tfreezed по причине возможного отказа соответствующего сенсорного датчика; удаление тех значений, которые не попадают в интервал допустимых значений [xmin, xmax], и значений, для которых интервал допустимых значений не определен, а z-score по модулю больше 3,29. 2. Регуляризация временного шага путем переноса последнего определенного показания сенсора на ближайший справа шаг регулярной временной сетки. 3. Заполнение образовавшихся после удаления выпадающих значений лакун во временных рядах с учетом величины подобной лакуны dt. То есть, если dt Полученные регуляризованные данные поступают затем на вход основного алгоритма прототипа, то есть используются при построении статистических моделей. Построение модели множества нормальных состояний ВК. Данное построение осуществляется в два этапа. На первом этапе все множество нормальных состояний разбивается на k кластеров, для чего в рассматриваемом прототипе используется более эффективный по сравнению с общеизвестным методом k-средних метод k-медоид [4] на основе алгоритма CLARA (оптимизированная с вычислительной точки зрения версия алгоритма PAM – partition around medoids). Как и все классические методы кластерного анализа, метод k-медоид предполагает априорное знание числа кластеров k, на которые нужно разбить исходное множество. Для нахождения этого числа на основе только входных данных была предложена концепция «силуэт кластера» и на ее основе – статистика g(i), позволяющая оценить качество разбиения множества на отдельные кластеры [5]. В рассматриваемом алгоритме построения мо-дели множества нормальных состояний ВК для нескольких значений числа кластеров М (как правило, это числа 1, …, 10, число М может меняться пользователем прототипа) происходит оценка ве-личины, обратной к На втором этапе построения модели происхо-дит описание границ каждого из кластеров Xi, по-лученных на первом этапе. Для этого в данной ра-боте с помощью метода опорных векторов нахо-дилось решение стандартной задачи о бинарной классификации, где в качестве дополнительного второго класса бралось центрально-симметричное к множеству Xi множество –Xi. В такой постановке эта задача эквивалентна задаче о классификации с одним классом [6], это позволило использовать полуэмпирические формулы для расчета апостериорных вероятностей, полученных в работе [7]. Построение модели регрессора. Как показало предварительное исследование статистических свойств данных мониторинга, они плохо описываются с помощью классических стандартных моделей, поэтому использование таких общеупотребительных параметрических моделей временных рядов, как VARX или SS, для осуществления прогнозирования возможных будущих состояний ВК представляется неэффективным. По этой причине в данной работе выбор был сделан в пользу методов, основанных на статистической теории машинного обучения, которые успели зарекомендовать себя как надежный и эффективный инструмент статистической обработки данных [7, 8]. Выбранный авторами метод SVR состоит в построении такой линейной функции в характеристическом пространстве, которая наилучшим образом приближала бы значения искомой функции. Для поиска такого приближения используется принцип минимизации структурного риска (structure risk minimization, SRM principle). Основными достоинствами непараметрических методов являются их универсальность и независимость от априорных знаний, что позволяет единообразно обрабатывать данные разной статистической природы. В настоящей работе были использованы два варианта метода SVR, которые в дальнейшем будем обозначать как метод p-svr и метод msvr. Метод p-svr заключается в последовательном применении метода ε-SVR [9] к каждой из компонент многомерного вектора. Тогда как метод msvr состоит в построении специальной функции стоимости L(u(i)), зависящей от всех компонент многомерного вектора, и решает задачу многомерной регрессии непосредственно с помощью итерационной квазиньютоновской процедуры [10]. Задача регрессии на основе подхода SVR в применении к задаче экстраполяции многомерных временных рядов переформулируется следующим образом: (X1, …, Xp)®Y1=Xp+1, (X2, …, Xp+1)®Y2=Xp+2, … (Xn, ..., Xp+nl-1)®Ynl=Xp+nl, (Xn+1, …, Xp+nl)ÞYnl+1, где nl – размер обучающей выборки; p – кратность интегрирования временного ряда; d – размерность изучаемого временного ряда со значениями XiÎÂd и YiÎÂd (i – момент времени), которые служат, со-ответственно, входными и выходными данными при обучении модели регрессора. Прогнозируе-мым значением является Ynl+1ÎÂd. Вычисление апостериорных вероятностей. Построение классификатора, способного оценить апостериорную вероятность попадания тестируе-мого объекта в определенный класс P(class|input), является важной задачей в теории машинного обучения. Это становится особенно необходимым, когда процесс классификации – одна из составных частей более сложного алгоритма. Однако метод SVM порождает на выходе не-прокалиброванные значения, которые не являются вероятностями. Поэтому для их вычисления необходимы дополнительные построения. В данной работе для оценки апостериорных вероятностей попадания прогнозируемого состояния ВК в множество нормальных состояний был использован алгоритм, реализующий эмпирический метод, ос-нованный на применении сигмоидной функции в качестве калибровочной [7]:
где параметры A и B подбираются методом максимального правдоподобия. Экспериментальное тестирование прототипа
Тестирование прототипа проводилось на осно-ве численных экспериментов с использованием данных мониторинга, собранных в течение неко-торого промежутка времени с реально действую-щих ВК. Такой набор данных после проведения процедуры первичной предобработки (регуляри-зации) далее будет называться моделью данных. Для имитации нештатных ситуаций в них добав-лялись искусственно созданные данные. Численный эксперимент, во-первых, исключает риск, связанный с выходом из строя ВК по причине программных сбоев во время тестирования, а во-вторых, использование модели данных позволяет контролировать процесс тестирования, когда, меняя модель данных или ее параметры, можно смоделировать различные режимы работы ВК. В тестировании были использованы данные, собранные системой мониторинга Infra-StruXure Central в течение одного дня с ВК с числом узлов около 1 000 и системой воздушного охлаждения на основе водяных кондиционеров (модель данных A) и системой мониторинга ganglia в течение 14 дней с ВК с числом узлов около 200 и системой непосредственного водяного охлаждения (модель данных B). В обоих случаях шаг сбора данных составил 1 минуту. Эти наборы, помимо длины временных данных, отличаются характером собранной в них информации, что связано с различием в подходах к реализации в двух ВК подсистем охлаждения и электропитания, а также составом собственно вычислительных подсистем и решаемых на них задач, что обусловливает различие в нагрузках на ВК. Модели данных A и B. Для набора данных A из всего набора сенсорных датчиков на основе опыта эксплуатации ВК был выбран поднабор, состоящий из 263 сенсоров 7 различных типов сенсорных датчиков, контроль за показаниями которых представляет наибольшую важность. Таким образом, в этот набор вошли температура модулей памяти, сила тока и общая потребляемая мощность тока на шкафных блоках распределителей питания, входная и выходная температура теплоносителя кондиционера. Из всего множества сенсоров, осуществляющих мониторинг ВК, в случае модели данных B авторами был выбран поднабор, состоящий из 315 сенсоров 4 различных типов сенсорных датчиков, контроль за показаниями которых представляется наиболее важным: температура процессоров, загруженность процессора, общая потребляемая мощность тока на шкафных блоках распределителей питания. На рисунках 1 и 2 приведены примеры типичного графика зависимостей от времени показаний сенсоров для моделей данных A и B соответственно. Выбор параметров модели прогнозирования. Известно, что обобщающая способность метода SVR (точность оценки) зависит от правильного выбора метапараметров: параметра регуляризации C, который определяет равновесие между сложностью модели регрессора и степенью допустимых отклонений, и параметра ε, задающего ширину нечувствительной зоны, используемой при обучении алгоритма, а также от параметров используемой кернел-функции. Этот выбор в большинстве случаев осуществляется эмпирическим путем на основе имеющегося опыта. Тем не менее делаются попытки предложить теоретически более обосно-ванные подходы к решению проблемы. Так, для кернел-функций гауссовского типа (rbf-методы) выбор параметра можно осуществить с помощью самих обучающих данных, для этого выбирается любое значение из интервала 0,1–0,9 квантилей случайной величины, соответствующей обучающим данным [11]. Параметр C, как правило, выбирают из области значений выходных данных. Однако такой выбор не учитывает влияние выпадающих значений. Для их учета можно использовать формулу
где Известно, что значение ε должно быть пропор-ционально уровню случайного шума во входных данных τ. Для учета влияния размера выборки на выбор ε в работе [12] была предложена полуэмпи-рическая формула
где nl – размер обучающей выборки; τ – параметр, описывающий порядок фонового шума. Изучение качества прогнозирования. Для тестирования качества прогнозирования данные мониторинга, представляющие собой отрезок временного ряда, разбивались на две части: данные с момента времени t0 до момента t0+MDt – выборка для построения модели множества нормальных состояний (выборка I), и данные с момента времени t0+(M+N+1-nl)Dt до момента t0+KDt – выборка для построения модели регрессора (выборка II). Для модели данных A значения N, M и K соста-вили 1134, 205, 1 439 соответственно. Для модели данных B эти значения составили 12 900, 205, 13 205 соответственно. Таким образом, в обоих случаях размер тестовой выборки для проверки работы регрессора равнялся 100. Данные между моментами времени t0+(M+N-nl)Dt и t0+(M+N)Dt использовались для инициализации работы алго-ритма регрессора. Длина временного шага была задана равной одной минуте для обеих моделей данных. Значения метапараметров методов msvr и p-svr вычислялись по формулам (2) и (3). Для метода p-svr значение метапараметра C было выбрано равным 1. Кроме различных значений метапараметров, в тестировании также использовались два варианта кернел-функции: линейной f(X, X¢)=áX, X¢ñ, где á,ñ – стандартное скалярное произведение в Ân, и гауссовой В качестве тестируемых величин, помимо предсказанных регрессором состояний X, были также выбраны полная вероятность попадания состояния X в множество нормальных состояний P(X)t, определяемая по формуле полной веро-ятности: В этих формулах индексное множество S обозначает множество кластеров, на которые разбивается все множество нормальных состояний ВК; P(i) – весовой коэффициент, равный отношению количества обучающих состояний, попавших в данный кластер, к общему числу обучающих данных; P(X|i) – апостериорная вероятность, вычис-ленная по формуле (1). Для оценки точности прогнозирования во всех тестовых запусках при разных значениях метапа-раметров, моделей данных и методов прогнозиро-вания были подсчитаны величины абсолютной погрешности вычисления P(X)t, P(X)m и X относи-тельно l0- и l2-нормы последовательностей по формуле ||DY(t)||i=||Yo(t)-Ys(t)||i, Y=Pt, Pm, X; i=0,2, а также была подсчитана нормированная среднеквадратичная погрешность нахождения последовательности прогнозируемых состояний X, вычис-ленная относительно l2-нормы последовательно-стей:
В этих формулах индекс o означает, что соответствующая величина была подсчитана для тестовых данных Xo (наблюдаемые значения), а индекс s относится к величинам Xs, рассчитанным с помощью модели регрессора (предсказанные значения). Xmean означает среднее от наблюдаемых значений. Таблица 1 Усредненные по всем метапараметрам метода значения ошибок вычисления вероятностей и показаний сенсорных датчиков для различных методов прогнозирования
Примечание. В таблице индексы g и l обозначают гауссову и линейную кернел-функцию соответственно. В таблице 1 приводятся результаты, усредненные по всем метапараметрам. Из приведенных результатов видно, что методы msvr и p-svr в среднем имеют схожие порядки погрешностей вне зависимости от выбранной кернел-функции. Основной вывод, который можно сделать из про- веденного экспериментального исследования, заключается в том, что при правильном выборе метапараметров с помощью выбранного подхода удается осуществлять прогнозирование возможных будущих состояний ВК с точностью 6–16 %. Обнаружение нештатных ситуаций. В рамках подхода, рассматриваемого в данной работе, определение нештатных состояний ВК происходит путем обнаружения новых состояний, то есть таких, которые сильно отличаются от данных, участвовавших в процедуре обучения алгоритма. Для того чтобы промоделировать подобную ситуацию, было взято такое разбиение данных модели B, при котором выборка II содержала бы данные, отличающиеся от данных выборки I. На рисунке 3 представлены типичные зависимости рассчитанных вероятностей от времени для моделей А (в варианте, когда выборки I и II содержали статистически сходные данные) и В (когда данные выборок I и II статистически различались).
Проверка устойчивости к сбоям в показаниях сенсоров. Сбои в показаниях сенсорных датчиков представляют серьезную проблему для эффективной работы всего прототипа, поэтому в данной работе было проведено тестирование алгоритма регуляризации входных данных с тем, чтобы выяснить влияние сбоев на работу прототипа. Тестирование заключалось в следующей процедуре: для модели данных A были выбраны два набора параметров регуляризации; при одном наборе параметров регуляризованные данные имеют более сглаженный характер (в дальнейшем будем называть его моделью данных A-I), а при другом –имеют искажения (модель A-II) (рис. 4). Затем для этих двух моделей данных изучалось качество прогнозирования, как это описано выше. Результаты экспериментальных исследований представлены в таблице 2. Таблица 2 Погрешности, вносимые в работу прототипа при появлении сбоев в показаниях сенсоров
В таблице используются следующие обозначения: наблюдаемые величины – величины, рассчитанные по показаниям сенсорных датчиков, моделируемые величины – величины, предсказанные прототипом: ||DPm||1=||PIm-PIIm||0, ||DPm||2=||PIm-PIIm||2 и т.д., где индексами I и II обозначены величины, рассчитанные для моделей данных A-I и A-II соответственно. Приведенные данные свидетельствуют о том, что процедура искажения данных (то есть переход от модели данных A-I к модели данных A-II) не вносит серьезных изменений в работу прототипа. Относительные ошибки составляют 0,2–4,3 % для моделируемых величин, то есть результат прогнозирования практически не меняется. Обсуждение результатов В ходе процесса регуляризации данных происходят сглаживание и усреднение показаний сенсорных датчиков. С одной стороны, такое преобразование входных значений позволяет снизить влияние отдельных выпадающих значений на качество как построения модели нормальных состояний (границы кластеров становятся более четко выраженными), так и прогноза (процесс обучения модели регрессора сопровождается уменьшением ошибок процедуры кросс-верификации), но, с другой стороны, при неправильном выборе параметров регуляризации входных данных существует опасность пропустить момент появления большого числа сенсоров, показания которых выходят за интервал допустимых значений.
Еще одним необходимым условием эффективной работы рассматриваемого алгоритма является корректное построение модели множества нормальных состояний, предпочтительно на большом статистическом материале, когда подмножества, из которых состоит все множество нормальных состояний, представляют собой кластеры с четко выраженной границей. В этом случае контролирующие параметры алгоритма Pt и Pm характеризуются меньшим разбросом значений, что позволяет увеличить точность предсказания момента наступления критического события tx. Задача обнаружения аномальных состояний ВК облегчается при увеличении скорости и массовости появления аномальных показаний сенсорных датчиков. И наоборот, в пограничных случаях (при малых по абсолютной величине углах тренда в показаниях сенсоров и/или при малом числе аномальных показаний) определение точных значений tx затрудняется, то есть этот вопрос требует дальнейшего рассмотрения и уточнения количественных критериев, предъявляемых к задаче классификации состояний ВК и необходимых для эффективной работы всего алгоритма. Наконец, немаловажное значение имеет точность прогнозирования возможных состояний ВК, которая, как показывают результаты, зависит не только от параметров используемых методов прогнозирования, но и от обрабатываемых данных. Так, большая величина относительной ошибки nRMSE в случае модели B по сравнению с мо- делью A, по-видимому, объясняется, с одной стороны, вырожденностью этих данных, которая характеризуется длинными участками близких значений, а с другой – резкими скачкообразными изменениями по порядку величины, превышающими среднюю величину последовательных разностей временного ряда. Это приводит к появлению вырожденных матриц, которые алгоритмы методов SVR строят во время своей работы, что может привести к увеличению погрешности. Таким образом, выбор набора сенсорных датчиков, используемых для контроля, с учетом их статистических свойств и важности является ключевым моментом. Требования к скорости расчета одной точки прогноза определяются в первую очередь скоростью необратимого разрушения оборудования ВК при катастрофическом отказе инженерных подсистем. Для современных ВК этот промежуток времени, как правило, составляет 1–2 минуты. Исходя из данного требования должен проводиться отбор всех остальных параметров рассматриваемого алгоритма: состав и число сенсорных датчиков, используемых в системе анализа (размерность задачи), параметры регуляризации входных данных (интервалы допустимых значений сенсорных датчиков и временные промежутки отсутствия данных мониторинга), количество и состав обучающей выборки для построения модели нормальных состояний и внутренние параметры метода кластеризации входных данных, а также метапараметры модели регрессора. Дополнительно скорость расчета одной точки прогноза можно увеличить путем перехода от решения задачи построения регрессии в так называемом batch-mode-режиме, когда эта модель полностью перестраивается при поступлении новых данных, к online-режиму, в котором изменению подлежит лишь малая часть модели, соответствующая вновь поступившим данным. В работе [13] был предложен алгоритм, реализующий online-режим для задачи одномерной регрессии. Однако на основе сведений, известных авторам, для задачи многомерной регрессии такого алгоритма пока не существует. Для перехода от прототипа к построению рабочей системы анализа требуется дальнейшее изучение влияния всех этих факторов на эффективность работы, поскольку характер рассматриваемых зависимостей довольно сложен. Таким образом, результаты тестирования прототипа системы анализа состояний ВК показывают, что при правильном выборе всех контролирующих параметров и наличии достаточного количества статистического материала подход на основе методов машинного обучения (метод SVM/SVR), рассмотренный в данной работе, позволяет осуществлять автоматизированное обнаружение аномальных состояний ВК. При этом данный алгоритм обладает определенной устойчивостью к сбоям в показаниях сенсорных датчиков и повышает точность предсказания наступления критической ситуации с ростом ее опасности. Количественный аспект этих вопросов требует дальнейшего уточнения. К достоинствам используемого в данной работе алгоритма стоит также отнести его модулярный характер, когда в каждом из шагов базового алгоритма (регуляризация входных данных – прогнозирование возможных будущих состояний ВК – классифицирование состояний ВК) возможно использование разных альтернативных методов. В частности, выбранные в данной работе методы SVM/SVR, помимо высокой вычислительной эффективности, являющейся следствием концептуальной простоты метода, сравнительно легко позволяют произвести усложнение выявляемых аномальных состояний, например, предсказывание коллективных аномалий [14]. Литература 1. Vapnik V.N., Statistical learning theory: NY: John Wiley \& Sons, 1998, 740 p. 2. RRDtool. Homepage. URL: http://oss.oetiker.ch/rrdtool/ (дата обращения: 25.04.2013). 3. Chandola V., Banerjee A., Kumar V. ACMachinery Computing Surveys, 2009, Vol. 41, no. 3. 4. Kaufman L., Rousseeuw P.J., Finding Groups in Data An Introduction to Cluster Analysis: NJ, Hoboken, USA: John Wiley \& Sons, 2005, 355 p. 5. Rousseeuw P.J., Computational and Applied Mathematics, 1987, Vol. 20, pp. 53–65. 6. Scholkopf B., Platt J.C., Shawe-Taylot J., Smola A.J., Williamson R.C., Neural Computation, 2001, Vol. 13, pp. 1443–1471. 7. Lin Hs.-T., Lin Ch.-J., Weng R.C., Machine Learning, 2007, Vol. 68, pp. 267–276. 8. Sapankevych N.I., IEEE Computational Intelligence Magazine, 2009, Vol. 5, pp. 25–38. 9. Smola A J., Scholkopf B., A Tutorial on Support Vector Regression. URL: http://eprints.pascal-network.org/archive/ 00002057/01/SmoSch03b.pdf (дата обращения: 25.04.2013). 10. Sánchez-Fernández M., Arenas-García J., Pérez-Cruz F., IEEE Transactions on Signal Processing, 2004, Vol. XX, no. V, pp. 100–123. 11. Cherkassky V., Ma Y., ICANN 2002, LNCS 2415, Springer-Verlag, Berlin-Heidelberg, 2002, pp. 687–693. 12. Caputo B., Sim K., Furesjo F., Smola A., Proc. of NIPS workshop on Statistical methods for computational experiments in visual processing and computer vision, Whistler, 2002. 13. Ma J., Theiler J., Perkins S., Neural Computation, 2003, Vol. 15, pp. 2683–2703. 14. Ma J., Perkins S., Proc. 9th ACM SIGKDD'03, Washington, DC, USA, 2003, pp. 613–618. References 1. Vapnik V.N., Statistical learning theory, NY, John Wiley & Sons, 1998. 2. RRDtool, available at: http://oss.oetiker.ch/rrdtool/ (accessed 25 April 2013). 3. Chandola V., Banerjee A., Kumar V., ACM Computing Surveys, 2009, Vol. 41, no. 3. 4. Kaufman L., Rousseeuw P.J., Finding Groups in Data An Introduction to Cluster Analysis, NJ, Hoboken, USA, John Wiley & Sons, 2005. 5. Rousseeuw P.J., Computational and Applied Mathematics, 1987, Vol. 20, pp. 53–65. 6. Scholkopf B., Platt J.C., Shawe-Taylot J., Smola A.J., Williamson R.C., Neural Computation, 2001, Vol. 13, pp. 1443–1471. 7. Lin Hs.-T., Lin Ch.-J., Weng R.C., Machine Learning, 2007, Vol. 68, pp. 267–276. 8. Sapankevych N.I., IEEE Computational Intelligence Magazine, 2009, Vol. 5, pp. 25–38. 9. Smola A J., Scholkopf B., A Tutorial on Support Vector Regression, available at: http://eprints.pascal-network.org/archive/ 00002057/01/SmoSch03b.pdf (accessed 25 April 2013). 10. Sánchez-Fernández M., Arenas-García J., Pérez-Cruz F., IEEE Transactions on Signal Processing, 2004, Vol. 20, no. 5, pp. 100–123. 11. Cherkassky V., Ma Y., ICANN 2002, LNCS 2415, Springer-Verlag, Berlin-Heidelberg, 2002, pp. 687–693. 12. Caputo B., Sim K., Furesjo F., Smola A., Proc. of NIPS workshop on Statistical methods for computational experiments in visual processing and computer vision, Whistler, 2002. 13. Ma J., Theiler J., Perkins S., Neural Computation, 2003, Vol. 15, pp. 2683–2703. 14. Ma J., Perkins S., Proc. 9th ACM SIGKDD'03, Washington, DC, USA, 2003, pp. 613–618. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?id=3579&like=1&page=article |
Версия для печати Выпуск в формате PDF (13.63Мб) Скачать обложку в формате PDF (1.39Мб) |
| Статья опубликована в выпуске журнала № 3 за 2013 год. [ на стр. 158-166 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:




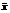 – среднее значение из выборки для случайной величины x; sd(x) – стандартное отклонение для этой выборки.
– среднее значение из выборки для случайной величины x; sd(x) – стандартное отклонение для этой выборки. , а затем в качестве опти-мального числа возможных кластеров выбирается то, которое дает максимальное значение статистики
, а затем в качестве опти-мального числа возможных кластеров выбирается то, которое дает максимальное значение статистики  . После чего алгоритм использует это значение как входной параметр для метода k-медоид. Такой подход позволяет автоматизировать процесс построения модели множества нормальных состояний.
. После чего алгоритм использует это значение как входной параметр для метода k-медоид. Такой подход позволяет автоматизировать процесс построения модели множества нормальных состояний. , (1)
, (1)
 , (2)
, (2) – среднее значение выходных обучающих данных; sy – стандартное отклонение.
– среднее значение выходных обучающих данных; sy – стандартное отклонение. , (3)
, (3)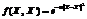 , где |·| – стандартная евклидова норма в Ân. Значение параметра σ рассчитывалось автоматически по обучающей выборке алгоритма.
, где |·| – стандартная евклидова норма в Ân. Значение параметра σ рассчитывалось автоматически по обучающей выборке алгоритма. , и максимальная вероятность попадания состояния X в один из кла-стеров множества нормальных состояний P(X)m, определяемая по формуле
, и максимальная вероятность попадания состояния X в один из кла-стеров множества нормальных состояний P(X)m, определяемая по формуле  .
.

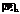




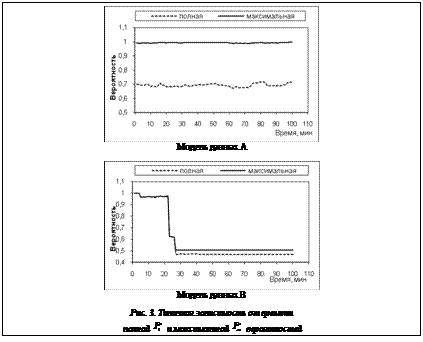 Тогда как для однородной модели A как полная, так и максимальная вероятности слабо меняются от времени, аналогичные кривые для модели B претерпевают характерный излом, резкое падение, ступеньку, связанную с отсутствием в обучающих данных модели нормальных состояний ВК, элементов, схожих с элементами выборки II.
Тогда как для однородной модели A как полная, так и максимальная вероятности слабо меняются от времени, аналогичные кривые для модели B претерпевают характерный излом, резкое падение, ступеньку, связанную с отсутствием в обучающих данных модели нормальных состояний ВК, элементов, схожих с элементами выборки II.






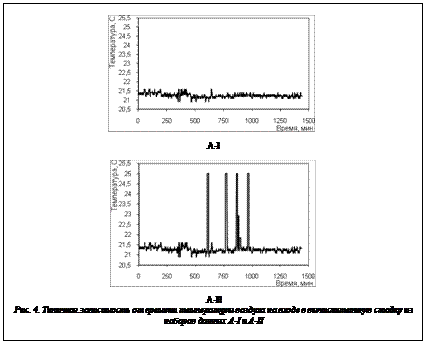 Тем не менее, как показывает опыт эксплуатации ВК, наиболее важным из всех возможных характеристик наблюдаемых значений сенсорных датчиков является наблюдение за их трендами, и вариант предподготовки данных с отбрасыванием отдельных выпадающих значений это допускает. Кроме этого, наличие небольшого числа (5–10 %) показаний сенсорных датчиков с выпадающими значениями не приводит к сильным изменениям в результатах прогнозирования и классификации состояний ВК, что, по-видимому, связано с большой размерностью решаемой задачи, поэтому для того, чтобы предложенный в данной работе алгоритм мог определить появление новых, аномальных состояний, необходимы серьезные изменения в показаниях сенсорных датчиков, то есть число выпадающих показаний сенсорных датчиков сравнимо с размерностью задачи – числом сенсорных датчиков, участвующих в контроле за системой мониторинга.
Тем не менее, как показывает опыт эксплуатации ВК, наиболее важным из всех возможных характеристик наблюдаемых значений сенсорных датчиков является наблюдение за их трендами, и вариант предподготовки данных с отбрасыванием отдельных выпадающих значений это допускает. Кроме этого, наличие небольшого числа (5–10 %) показаний сенсорных датчиков с выпадающими значениями не приводит к сильным изменениям в результатах прогнозирования и классификации состояний ВК, что, по-видимому, связано с большой размерностью решаемой задачи, поэтому для того, чтобы предложенный в данной работе алгоритм мог определить появление новых, аномальных состояний, необходимы серьезные изменения в показаниях сенсорных датчиков, то есть число выпадающих показаний сенсорных датчиков сравнимо с размерностью задачи – числом сенсорных датчиков, участвующих в контроле за системой мониторинга.