В промышленности очень часто возникает задача контроля и улучшения качества изделий. Для ее решения необходимо обнаруживать и локализовывать дефекты в выпускаемой продукции или в сырье. В данной статье рассматривается предметная область, связанная с обработкой алмазного сырья с целью получения драгоценных камней. Обрабатываемые алмазы имеют различные дефекты, образовавшиеся внутри кристаллов в процессе их роста. Для максимизации стоимости полученных драгоценных камней необходимо обнаружить дефекты внутри алмазного сырья и отсечь их при распиле на драгоценные камни. Основными дефектами являются инородные включения минералов, воздуха, а также трещины. Поскольку алмазное сырье обладает высоким коэффициентом преломления и сложной геометрической формой, обнаружение включений сильно затруднено. Для того чтобы включения были лучше видны, алмаз запаивается в иммерсионный куб с показателем преломления, близким к показателю преломления алмаза (рис. 1).
 Иммерсионный куб с алмазом подсвечивается специальным образом, что позволяет максимизировать контраст наблюдаемых дефектов. Иммерсионный куб фотографируется с различных ракурсов. Задача состоит в обнаружении и сегментации дефектов на полученных фотоизображениях. Помимо изображений, заданы геометрия алмаза и иммерсионного куба, их коэффициенты преломления, параметры фотокамеры (положение, ориентация относительно алмаза и т.п.).
Иммерсионный куб с алмазом подсвечивается специальным образом, что позволяет максимизировать контраст наблюдаемых дефектов. Иммерсионный куб фотографируется с различных ракурсов. Задача состоит в обнаружении и сегментации дефектов на полученных фотоизображениях. Помимо изображений, заданы геометрия алмаза и иммерсионного куба, их коэффициенты преломления, параметры фотокамеры (положение, ориентация относительно алмаза и т.п.).
Обзор существующих методов
Задача обнаружения и сегментации объектов является очень распространенной в области компьютерного зрения. Существующие алгоритмы часто используют априорную информацию об искомых объектах, например, об их форме, размере, цвете, о контрастности границы и т.п. Что касается включений, то их форма и размер могут сильно варьироваться, граница может быть как четкой, так и размытой. Единственная информация, которую можно достоверно использовать, – это относительная яркость (чем темнее область на фотографии, тем вероятнее, что это дефект). Для подобных задач применяются различные алгоритмы бинаризации изображений: глобальные, когда имеется один общий порог, и локальные (например, алгоритм симметричного локального порога [1], вычитание из размытого изображения). Суть алгоритмов в том, что в них различными способами оценивается яркость фона изображения, которая затем вычитается из исходного изображения. Основной сложностью для этих алгоритмов в задаче обнаружения включений является сильная вариация яркости фона, обусловленная сложной геометрией алмаза. Другой распространенный подход заключается в сегментации изображения с последующей классификацией областей по признакам, однако трудно выбрать эти признаки, так как априорной информации об искомых объектах мало. Алгоритм максимально стабильных экстремальных регионов [2] позволяет разбить изображение на набор вложенных друг в друга областей и выбрать максимально стабильную, соответствующую наиболее вероятному положению искомого объекта. Данный алгоритм хорошо работает в случае дефектов с контрастной границей, в других ситуациях граница дефекта может быть найдена неверно. Аналогичные проблемы возникают при подходах на основе классификации областей, полученных сегментацией типа «змея» [3]. Используемый в подходе признак, основанный на однородности градиента изображения вдоль границы объекта, в задаче поиска включений оказывается малоприменимым в силу различной степени размытости частей границы. Методы на основе классификации областей в скользящем окне (например [4]) не применяются для поиска дефектов в силу разного размера и произвольной формы. Таким образом, наиболее перспективными являются алгоритмы на основе оценки фона.
Описание предлагаемого алгоритма
Предлагаемый в данной работе алгоритм базируется на идее оценки яркости фона изображения, а также на стандартном подходе к сегментации изображения с последующей классификацией областей с использованием признаков на основе яркости восстановленного фона. Для оценки фона, помимо фотографии алмаза в иммерсионном кубе, используется описанная далее физическая модель расчета яркости на фотографии. Иммерсионный куб находится между равномерным источником света и фотокамерой, поэтому основная доля энергии от источника света теряется за счет поглощения энергии иммерсионным стеклом (алмаз практически не поглощает энергию). При этом энергия от источника счета зависит экспоненциально от длины хода луча в иммерсионной среде: Is(x, y)=I0×exp(–a×d), где Is – яркость изображения; I0 – яркость источника света; d – длина хода луча света в иммерсионной среде. Коэффициент затухания энергии a>0 неизвестен, однако его можно оценить по одной фотографии, поскольку длину хода луча можно легко рассчитать для каждого пикселя фотографии. Данная модель довольно проста, чтобы служить оценкой фона изображения, поскольку в реальности яркость источника света может быть не константой для всех точек изображения, имеются различные внешние источники влияния (блики, отражения) и т.п. Тем не менее она верно передает различные перепады яркости в фоне изображения. Для построения финальной оценки фона используется двухмерный сплайн с пространственной вариацией гладкости. Искомая оценка фона представляется в виде линейной комбинации радиально-базисных функций [5]: I(P)=Swi×exp(–mi×r(P, Pi)), где P – рассматриваемая точка изображения (x, y); Pi (i= ) – одна из опорных точек сплайна; r(×,×) – квадрат евклидова расстояния между точками; wi>0 – вес опорной точки; mi>0 – коэффициент гладкости сплайна в опорной точке.
) – одна из опорных точек сплайна; r(×,×) – квадрат евклидова расстояния между точками; wi>0 – вес опорной точки; mi>0 – коэффициент гладкости сплайна в опорной точке.
Рассмотрим процесс построения сплайна. Изображение разбивается равномерной сеткой, в узлах которой помещаются опорные точки сплайна. Далее для каждой опорной точки оценивается гладкость mi. Для этого в локальной окрестности рассматриваемой точки строится сплайн с постоянной гладкостью m для простой оценки фона Is. Перебирая различные m, находим максимально возможное значение, при котором максимальная погрешность аппроксимации яркости в окрестности точки меньше некоторого порога T. Это значение и будет искомой гладкостью mi. Веса wi находятся путем решения системы линейных алгебраических уравнений, описанной в [5]. Таким образом, получена оценка фона изображения, которая одновременно учитывает перепады яркости фона по простой физической модели и яркость исходного изображения.
Следующий этап алгоритма – сегментация и классификация областей. В отличие от тради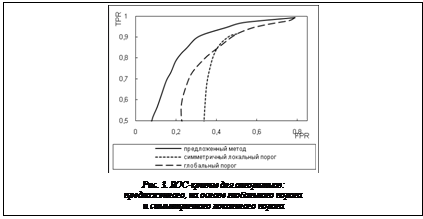 ционного подхода, когда сегментируется исходное изображение, предлагается сегментировать разность полученной оценки фона и исходного изображения. Полученные области классифицируются методом опорных векторов на основе нескольких признаков, среди которых можно выделить различные квантили разности оценки фона и исходного изображения по области, а также отношение средней яркости исходного изображения по области сегмента к средней интенсивности фона по области всего алмаза. Выход классификатора калибруется алгоритмом Платта [6]. По результатам этого этапа получается карта вероятности нахождения дефекта (пример результата работы
ционного подхода, когда сегментируется исходное изображение, предлагается сегментировать разность полученной оценки фона и исходного изображения. Полученные области классифицируются методом опорных векторов на основе нескольких признаков, среди которых можно выделить различные квантили разности оценки фона и исходного изображения по области, а также отношение средней яркости исходного изображения по области сегмента к средней интенсивности фона по области всего алмаза. Выход классификатора калибруется алгоритмом Платта [6]. По результатам этого этапа получается карта вероятности нахождения дефекта (пример результата работы 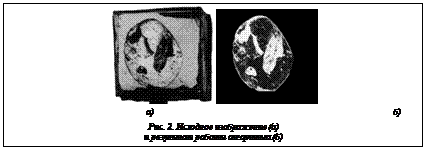 алгоритма представлен на рисунке 2).
алгоритма представлен на рисунке 2).
Тестирование алгоритма на реальных данных
Для обучения классификатора и тестирования алгоритма были размечены дефекты на изображениях различных алмазов (всего размечено около 30 фотографий, половина из которых использо- вались для обучения алгоритма). Для оценки алгоритма рассчитывалось общее число ложно найденных, а также ненайденных пикселей (результаты сведены на рисунке 3 в ROC-кривую). Предложенный алгоритм сравнивался с подхо- дами на основе оценки фона: применением глобального порога и алгоритмом симметричного локального порога [1] (брался радиус, равный половине линейного размера алмаза). Данные графики показывают, что простой глобальный порог в среднем работает лучше адаптивного порога, а предложенный алгоритм обладает большей точностью, чем существующие алгоритмы.
Таким образом, в данной статье представлен новый алгоритм обнаружения и сегментации дефектов в полупрозрачных минералах на основе оценки яркости фона изображения. Результаты сравнения предложенного алгоритма с аналогами показали, что данный алгоритм обладает большей точностью.
Литература
1. Veit T., Tarel J.-P., Nicolle P., Charbonnier P., Evaluation of road marking feature extraction, Intelligent Transportation Systems, 2008, ITSC 2008, 11th International IEEE Conference on. IEEE, 2008, pp. 174–181.
2. Matas J., Chum O., Urban M., Pajdla T., Robust wide baseline stereo from maximally stable extremal regions, British machine vision conference, 2002, Vol. 1, pp. 384–393.
3. Saha B.N., Ray N., Zhang H., Computing oil sand particle size distribution by snake-PCA algorithm, ICASSP, 2008, pp. 977–980.
4. Viola P., Jones M.J., Snow D., Detecting pedestrians using patterns of motion and appearance, Computer Vision, 2003, Proc. 9th IEEE Intern. Conf. IEEE, 2003, pp. 734–741.
5. Bookstein F.L., Principal warps: Thin-plate splines and the decomposition of deformations, IEEE Transactions on. Pattern Analysis and Machine Intelligence, 1989, Vol. 11, no. 6, pp. 567–585.
6. Platt J., Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods, Advances in large margin classifiers, 1999, Vol. 10, no. 3, pp. 61–74.
References
1. Veit T., Tarel J.-P., Nicolle P., Charbonnier P., 11th Int. IEEE Conf. on Intelligent Transportation Systems, IEEE, 2008, pp. 174–181.
2. Matas J., Chum O., Urban M., Pajdla T., British machine vision conf., 2002, Vol. 1, pp. 384–393.
3. Saha B.N., Ray N., Zhang H., ICASSP, 2008, pp. 977–980.
4. Viola P., Jones M.J., Snow D., Proc. of 9th IEEE Int.l Conf. on Computer Vision, IEEE, 2003, pp. 734–741.
5. Bookstein F.L., IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, Vol. 11, no. 6, pp. 567–585.
6. Platt J., Advances in large margin classifiers, 1999, Vol. 10, no. 3, pp. 61–74.




 ) – одна из опорных точек сплайна; r(×,×) – квадрат евклидова расстояния между точками; wi>0 – вес опорной точки; mi>0 – коэффициент гладкости сплайна в опорной точке.
) – одна из опорных точек сплайна; r(×,×) – квадрат евклидова расстояния между точками; wi>0 – вес опорной точки; mi>0 – коэффициент гладкости сплайна в опорной точке. ционного подхода, когда сегментируется исходное изображение, предлагается сегментировать разность полученной оценки фона и исходного изображения. Полученные области классифицируются методом опорных векторов на основе нескольких признаков, среди которых можно выделить различные квантили разности оценки фона и исходного изображения по области, а также отношение средней яркости исходного изображения по области сегмента к средней интенсивности фона по области всего алмаза. Выход классификатора калибруется алгоритмом Платта [6]. По результатам этого этапа получается карта вероятности нахождения дефекта (пример результата работы
ционного подхода, когда сегментируется исходное изображение, предлагается сегментировать разность полученной оценки фона и исходного изображения. Полученные области классифицируются методом опорных векторов на основе нескольких признаков, среди которых можно выделить различные квантили разности оценки фона и исходного изображения по области, а также отношение средней яркости исходного изображения по области сегмента к средней интенсивности фона по области всего алмаза. Выход классификатора калибруется алгоритмом Платта [6]. По результатам этого этапа получается карта вероятности нахождения дефекта (пример результата работы  алгоритма представлен на рисунке 2).
алгоритма представлен на рисунке 2).