Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Решение обратных краевых задач в кусочно-однородных средах методом регуляризации
Аннотация:
Abstract:
| Автор: Яремко О.Э. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 10318 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
Задача о структуре нестационарного температурного поля в двухслойной бесконечной пластине: пусть функция Задача о структуре нестационарного температурного поля в двухслойной бесконечной пластине по идеальным условиям сопряжения
и по начальным условиям
Рассмотрим обратную (ретроспективную) задачу: найти закон распределения температуры Как показано в работе М.П. Ленюка «Интегральные преобразования Фурье для кусочно-однородных неограниченных и полуограниченных сред» (К. 1985), выражение для
Действуем на систему (4) преобразованием Фурье на оси с точкой сопряжения: В образах Фурье получим
Применим метод регуляризации (см.: А.Н. Тихонов, В.Я. Арсенин. Методы решения некорректных задач. М. 1979). Для рассматриваемой задачи выбран стабилизирующий множитель:
где h – величина шага сетки, на которой ищется решение системы (4). Образ Фурье регуляризованного решения имеет вид Действуем обратным преобразованием Фурье на оси с точкой сопряжения
Интегралы в преобразованиях Фурье аппроксимированы по формуле прямоугольников. Задача гравиразведки в двухслойной области: пусть функция Пусть в слое
При этом на прямой x=0 выполняются идеальные условия сопряжения:
На поверхности Земли (y=0) величина
Для численного решения рассмотренной задачи может быть использован метод регуляризации. Все программы, реализующие численное решение рассмотренных задач, написаны на языке Турбо Паскаль (Свид. о госрегистрации комплекта программ для ЭВМ № 50200601996). |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=364&page=article |
Версия для печати Выпуск в формате PDF (2.31Мб) |
| Статья опубликована в выпуске журнала № 3 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- К вопросу параметризации свойств программных средств обучения
- Система автоматизации процессов рабочего проектирования сложного изделия
- Инструментальные средства управления эффективностью использования инвестиционных ресурсов в процессе реализации проекта
- Адаптивная компиляция на основе данных профилирования
- Системы компьютерной поддержки процессов анализа, синтеза и планирования решений в условиях неопределенности
Назад, к списку статей




 ограничена в области
ограничена в области 
 , где
, где  – единичная функция Хевисайда.
– единичная функция Хевисайда. приводит к построению ограниченного в области
приводит к построению ограниченного в области  (1)
(1)
 (2)
(2) (3)
(3) в начальный момент по известному закону распределения температуры
в начальный момент по известному закону распределения температуры 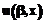 в момент времени
в момент времени  .
.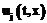 имеет вид:
имеет вид: (4)
(4)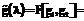

 . (5)
. (5)
 .
.


 ограничена в области
ограничена в области 
 , где
, где  (y – глубина под поверхностью Земли) расположены источники аномального гравитационного поля, а при
(y – глубина под поверхностью Земли) расположены источники аномального гравитационного поля, а при  их нет; x – горизонтальная координата;
их нет; x – горизонтальная координата; 

 – потенциал гравитационного поля при
– потенциал гравитационного поля при  . Тогда потенциал поля
. Тогда потенциал поля  в области
в области  является гармонической функцией:
является гармонической функцией: (6)
(6) . (7)
. (7)
 . (8)
. (8) может быть измерена:
может быть измерена:  ,
, 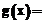
 . Требуется найти потенциал поля при y=h, то есть
. Требуется найти потенциал поля при y=h, то есть  ,
,  . Получим сепаратную систему интегральных уравнений Фредгольма I рода относительно искомых функций
. Получим сепаратную систему интегральных уравнений Фредгольма I рода относительно искомых функций 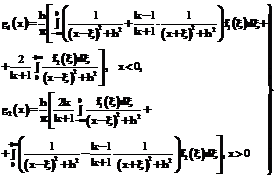 (9)
(9)