Об одном подходе к оценке качества обработки видеографической информации
| Кольцов П.П. (koltsov@niisi.msk.ru) - НИИСИ РАН, г. Москва, г. Москва, Россия, доктор технических наук | |
| Ключевые слова: специфичность, чувствительность, сегментация, реставрация изображений, выделение границ, эталонные изображения, обработка изображений |
|
| Keywords: specificity, sensitivity, segmentation, image restoration, edge detection, reference images, image processing |
|
|
|
|
В данной работе описывается подход к обработке видеографической информации, сложившийся к настоящему времени в отделе обработки и распознавания видеографической информации НИИСИ РАН. Сначала тематика исследовательских работ отдела, созданного четверть века назад, была ориентирована на конкретные прикладные проблемы, связанные с попытками создания автоматических и автоматизированных технических систем для решения задач интеллектуальной обработки видеографической информации. На основе созданной в отделе 3D-модели отображения земной поверхности в реальном масштабе времени [1] был разработан многомашинный макет автоматизированной системы мониторинга земной поверхности ДЕДАЛ [2], предназначенной для дистанционного обнаружения и распознавания движущихся объектов. Необходимо также отметить разработанную компьютерную систему ПРИЗМА [3], позволяющую по заданному набору изображений и эталонов подбирать методы их обработки, а также генерировать предметно-ориентированную систему понимания изображений. Логика исследовательских работ отдела привела к пониманию необходимости построения системы оценки качества работы программных средств обработки видеографической информации, позволяющей делать обоснованный выбор из них наиболее адекватных условиям решения задачи. В рамках построения такой системы была выработана идеология сравнительного исследования разнообразных методов обработки растровых изображений, позволяющая реализовать адаптивную технологию проектирования прикладных технических систем понимания изображений. Эта идеология, являющаяся своеобразным результатом исследовательской активности отдела, и будет представлена в данной статье. Эталонные изображения. Основным требованием к такой универсальной оценке является возможность ее получения вне зависимости от конкретного метода, используемого для решения задачи обработки видеографической информации. Это требование может быть удовлетворено, если все методы оцениваются на одном и том же видеографическом материале. Но возникает вопрос, как формировать этот материал. В основу формирования такого материала, называемого эталонными, или тестовыми, изображениями, легли следующие принципы. 1. Эталонные изображения должны содержать максимально полный набор сложных для работы рассматриваемых методов обработки видеографической информации элементов. 2. 3. Для эталонных изображений должна существовать возможность внесения контролируемых деградаций, позволяющих выявлять особенности поведения рассматриваемых методов обработки видеографической информации при различных внешних условиях. 4. Для всех эталонных изображений известно заданное априори точное решение задачи обработки видеографической информации – ground truth. Формирование набора эталонных изображений для конкретных задач обработки видеографической информации, удовлетворяющих этим принципам, по сути является неформальной задачей, поскольку и полнота, и сложность плохо поддаются формализации. В такой ситуации разработка эталонных изображений основана на практическом опыте разработчика, а сам набор изображений является открытым. Необходимость внесения контролируемой деградации в эталонные изображения связана с тем, что реальные изображения, как правило, подвержены искажениям, привносимым внешними условиями и особенностями получения изображения в цифровом виде. Обычными источниками деградации являются зашумление и размытие. Оценка качества. Для эталонных изображений, подобранных в соответствии с описанными принципами, в качестве универсальной оценки качества решения задачи обработки видеографической информации можно взять некоторую меру отличия результатов обработки этой информации от ground truth. Необходимо отметить, что выбор конкретной меры определяет содержательную интерпретацию получаемых оценок. В частности, можно брать меры отличия, полученные на основе метрик Евклида, Хаусдорфа, статистических, нечетких мер и т.п. Рассмотрим реализацию декларированного выше подхода для получения универсальной оценки качества работы ряда программных реализаций известных методов решения задач выделения границ и реставрации изображений. Выделение границ. В качестве набора искусственных изображений для оценки программных реализаций методов выделения границ был взят набор, приведенный на рисунках 1–3. Для эталонных изображений на рисунках 1 и 2 границами являются прямые линии, а величина скачка яркости вдоль границы изменяется по линейному закону. Эталонное изображение в левой части рисунка 3 имеет границу переменной кривизны и изменение скачка яркости, аналогичное приведенному выше. В правой части рисунка 3 приведено эталонное изображение с пересекающимися линейными границами. Слабоконтрастные границы, близкое расположение разных объектов, схождение нескольких границ в одной точке усложняют работу программ, предназначенных дл Поскольку программы решения задачи реставрации изображений должны хорошо сохранять резкие перепады яркости и подавлять шум на естественных изображениях, все перечисленные эталонные изображения можно использовать и для оценки качества работы этих программ.
Можно видеть, что программные реализации Canny и Heitger имеют хорошую чувствительность и более устойчивы к белому шуму, то есть меньше теряют истинных граничных точек по сравнению с другими реализациями. К тому же программные реализации Canny и Rothwell обладают явно лучшей специфичностью, в то время как все остальные показывают примерно в равной степени плохие результаты, то есть на каждую найденную ими точку истинной границы приходится слишком много точек, к границе не относящихся, но отнесенных к ней программами. Реставрация. В рамк Из рисунка видно, что все программные реализации обеспечивают подавление шума, поскольку графики в основном располагаются ниже пунктирной линии. Таким образом, обработанное изображение ближе к ground truth, чем зашумленное. Кроме того, программные реализации методов Гемана–Рейнольдса и метода с кусочно-линейной функцией эффективнее реализации метода Мамфорда–Шаха при сильном шуме. В свою очередь, реализация метода Мамфорда–Шаха лучше работает при малых шумах.
Аффинные преобразования. Рассматриваемый подход к получению универсальной оценки качества работы программ обработки видеографической информации можно применить для изучения устойчивости работы программ выделения границ относительно аффинных преобразований исходных изображений. Актуальность таких исследований очевидна, поскольку ориентация объектов на изображении относительно краев может быть произвольной, а реализации методов выделения границ к этим краям привязаны. В качестве эталонных изображений естественно было взять изображения, использованные при исследовании программ выделения границ, а аналогом деградации в рассматриваемом случае являются собственно аффинные преобразования. На рисунке 10 приведены пример эталонного изображения узел и результаты его обработки методом Smith до и после поворота на 45°. В этом случае чувствительность Se, специфичность Sp и расстояние Хаусдорфа H принимают значения, приведенные в таблице 1. Таблица 1
Сегментация изображений. Для задач сегментации изображений хорошие программы сегментации – так называемые сегментаторы – должны выделять те области на изображении, в которых могут находиться содержательно значимые объекты. Желательно, чтобы эти области содержали смысловые объекты изображения, а границы между областями соответствовали реальным границам объектов. В качестве сегментаторов, для которых была построена универсальная оценка качества их работы, рассмотрены EDISON, JSEG, EDGEFLOW и MULTISCALE [9]. Одним из сложных случаев для сегментаторов является наличие углов на изображении. И такие ситуации нельзя считать исключительными. В этой связи в набор эталонных изображений были включены соответствующие изображения, примеры которых приведены на рисунке 11.
На рисунке 13 приведен график зависимости от величины угла расстояния между истинным положением вершины угла и ближайшей точкой угла после работы сегментатора. Как видим, чем острее угол, тем больше могут быть искажения. При этом сегментатор EDGEFLOW при больших углах предпочтительнее сегме Было также рассмотрено поведение сегментаторов на областях с медленно изменяющейся яркостью, обычно приводящее к выделению сегментаторами ложных границ объектов. В качестве контролируемой деградации рассматривались зашумление и размытие. В этом случае лучшее качество показал сегментатор JSEG. Использование размытых мет Как видим, только программная реализация Canny позволила выявить все угловые точки, являющиеся узловыми для данного изображения. Однако при использовании оценок Se, Sp и H качество результатов работы неразличимо. Таким образом, использование классических метрик не выявляет преимущество программной реализации метода Canny, не пропустившей угловые точки квадрата. В этом случае введение понятия нечеткого эталонного изображения и использование нечетких метрик позволили получить оценки качества для различных реализаций методов выделения границ, обладающих особенностями, сложными для их работы.
ражений в нечеткие необходимо снабдить их этими функциями. Очевидно, что если эти функции принадлежности будут подчеркивать значимость пикселов в особенностях границы объекта, то нечеткие метрики должны уловить различие в работе программ, выделяющих границы, относительно этих особенностей. Рассмотрим приведенный на рисунке 14а квадрат 5´5 пикселов. Можно видеть, что граничные точки относятся к двум классам: A1 – вертикальные и A2 – горизонтальные. Определим для этих классов две функции принадлежности, которые на всех граничных пикселах равны 0,8, а в угловых – 1. Формирование нечеткого эталонного изображения завершено. В качестве меры близости между результатами работы программ и нечетким эталоном рассматривались введенные в [11] величины ОА1 и ОА2:
где fAk(x) – функции принадлежности нечеткого эталона классу Ak; fBk(x) – функции принадлежности для результатов работы программы выделения границ; x – пикселы. Отметим, что в рассматриваемом примере функция принадлежности результатов работы программ является вырожденной, принимающей значение 1 только на определенных программой граничных пикселах. Полученные данные приведены в таблице 2. Таблица 2
Программная реализация метода Canny дает более предпочтительные результаты, чем программная реализация метода Rothwell, что вполне согласуется с визуальным восприятием этих результатов. Таким образом, можно утверждать, что использование нечетких мер сходства и расширение понятия эталонных изображений до нечетких позволяют более полно выявлять особенности сравниваемых программ. Текстурный анализ. Рассмотрим применение идеологии получения универсальной оценки качества работы различных программных реализаций методов, используемых при решении задач текстурного анализа, например, задачу выделения на изображении текстур. В качестве эталонных изображений, представляющих сложность для работы программ выделения текстур, взяты естественные и искусственные изображения. На рисунке 15 приведен пример из набора искусственных эталонных изображений. Для сложных ситуаций в работе программ выделения текстурных областей набор искусственных эталонных изображений создан таким образом, чтобы в пределах текстурных областей могли меняться размер текстуры, а также контраст границы между текстурной и бестекстурной облас- тями. Для получения значений универсальной оценки качества работы были взяты программные реализации метода плотности локальных экстремумов, метода MAXDIF и метод плотности граничных точек [12]. Для численной оценки качества работы этих программ использован модифицированный показатель качества Пратта (FOM) [12], обычно используемый в текстурном анализе:
где N – число пикселов изображения; di – евклидово расстояние между i-м пикселом изображения после работы метода и его истинной областью (текстурной или бестекстурной); γ – постоянный шкалирующий множитель, который может использоваться для изменения вклада ошибок в FOM. Контролируемая деградация в эталонные изображения не вносилась. На рисунке 16 приведены полученные результаты для реализаций методов плотности граничных точек (1), плотности локальных экстремумов (2) и MAXDIF (3). Видно, что различия между качеством работы программ реализации методов плотности граничных точек и MAXDIF несущественны, тогда как программа реализации метода плотности локальных экстремумов показала худший результат. Инструментальные средства. Изложенные выше результаты исследований по оценке качества работ программ, решающих разнообразные задачи обработки видеографической информации, были получены с помощью специально разработанных инструментальных систем PETRA (Performance Evaluation of Texture Recognition Algorithms) [12] и PICASSO (PICture Algorithms Study SOftware) [4]. Система PETRA ориентирована на работу с программами обработки текстур и включает следующие этапы. 1. Выбор программ, подлежащих сравнительному исследованию. 2. Выбор из базы эталонных изображений или генерация искусственных эталонных изображений, моделирующих текстуру, определяемую пользователем системы. 3. Выделение текстурных областей исследуемыми программами на эталонных изображениях. 4. Измерение качества получаемых результатов с помощью выбранной метрики. Статистическая обработка результатов. Система PICASSO ориентирована на работу с программами предварительной обработки изображений (выделение границ, реставрация, сегментация и т.п.) и имеет следующую структуру. 1. Выбор программ, подлежащих сравнительному исследованию. 2. Выбор из базы эталонных изображений или генерация искусственных эталонных изображений, моделирующих требуемые ситуации, определяемые пользователем системы. 3. Выбор вариантов деградации эталонных изображений. 4. Решение задач предварительной обработки изображений исследуемыми программами. 5. Измерение качества получаемых результатов с помощью выбранной метрики. 6. Статистическая обработка результатов. Отметим, что отсутствие возможности выполнить деградацию (обычно зашумление) эталонных текстурных изображений связано с известной высокой неустойчивостью программ обработки текстур к такому воздействию. Инструментальные системы PETRA и PICASSO являются практической реализацией рассмотренной в данной статье системы оценки качества работы программных средств обработки видеографической информации. Обе системы успешно прошли апробацию и подтвердили эффективность предложенного подхода, результаты которого отражены в публикациях [13, 14]. В заключение отметим следующее. В работе изложена идеология прямого тестирования программ обработки видеографической информации. На базе стандартизованного набора изображений, называемых эталонными, находится универсальная оценка качества результатов работы программ обработки видеографической информации. Полученные сопоставимые оценки качества позволяют ранжировать эти программы для последующего отбора наиболее эффективных. Внесение контролируемых деградаций в эталонные изображения дает возможность прогнозировать качество работы программ в условиях реальной эксплуатации. Исследование результатов работы фиксированной программы при варьировании ее управляющих параметров позволяет выявлять границы при- менимости программы. Изложенная идеология прямого тестирования программ обработки видеографической информации может быть распространена и на иные программные продукты, если существует множество моделей решения одной и той же задачи обработки информации. Следует упомянуть, что нацеленность работ, выполняемых в отделе, на практическое применение привела к расширению тематики тестирования программных изделий для обработки видеографической информации до тестирования изделий микроэлектроники [15]. Литература 1. Арабов И.И., Захаров А.В., Кольцов П.П., Кото- вич Н.В., Кравченко А.А., Куцаев А.С., Николаев В.К., Павловская Е.Я. Реализация и исследование пространственного изображения в реальном времени. М.: НИИСИ РАН, 1994. 14 c. 2. Грибков И.В., Захаров А.В., Кольцов П.П., Кото- вич Н.В., Кравченко А.А., Куцаев А.С., Николаев В.К. Автоматизированная система мониторинга земной поверхности DEDAL-2 // Интегральная геометрия. Математические модели. Понимание изображений. М.: НИИСИ РАН, 2001. С. 5–50. 3. Gribkov I., Koltsov P., Kotovich N., Kravchenko A., Koganov A., Kutsaev A., Nikolaev V., Zakharov A. PRIZM: Generator of Image Understanding Systems, Pattern Recognition and Image Analysis Systems, 2000, vol. 10, no. 1, pp. 143–149. 4. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchen- ko A.A., Kutsaev A.S., Nikolaev V.K., Zakharov A.V. PICASSO – system for evaluating edge detection algorithms, Pattern Recognition and Image Analysis, 2003, vol. 13, no. 4, pp. 617–622. 5. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchen- ko A.A., Kutsaev A.S., Nikolaev V.K., Zakharov A.V. Testing of Energy Minimizing Methods in Image Preprocessing Using the PICASSO System, Proc. 8th World MultiConf. on Systemics, Cybernetics and Informatics, 2004, vol. 6, pp. 233–238. 6. Isard M., Blake A. Active Contours: The Application of Techniques from Graphics, Vision, Control Theory and Statistics to Visual Tracking of Shapes in Motion. Berlin, Springer, 2000. 7. Kass M., Witkin A., Terzopoulos D. Snakes: Active Contour Models, Int'l J. Computer Vision, 1988, vol. 1, no. 4, pp. 321–331. 8. Xu Ch., Prince J.L. Snakes, Shapes and Gradient Vector Flow. IEEE Transactions on Image Processing, 1998, vol. 7, no. 3, pp. 359–369. 9. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchen- ko A.A., Kutsaev A.S., Osipov A.S., Zakharov A.V. Study of Noisy and Blurry Images Segmentation. Proc. 9 Int. Conf. on Pattern Recognition and Image Analysis: New Information Technologies (PRIA-9-2008), 2008, vol. 1, pp. 193–196. 10. Pal S.K., Madjumadar D.D. Fuzzy Mathematical Approach to Pattern Recognition. NY, Wiley, 1986. 11. Jäger G., Benz U. Measures of Classification Accuracy Based on Fuzzy Similarity. IEEE Trans. On Geoscience and Remote Sensing, 2000, vol. 38, no. 3, pp. 1462–1467. 12. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchenko A.A., Kutsaev A.S., Osipov A.S., Zakharov A.V. Performance evaluation of Texture Segmentation Methods. Proc. 13th World MultiConf. on Systemics, Cybernetics and Informatics, 2009, vol. 4, pp. 137–142. 13. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchenko A.A., Kutsaev A.S., Osipov A.S., Zakharov A.V. Comparative Study of Image Segmentation Algorithms. Proc. 8th WSEAS Int. Conf. on Signal, Speech and Image Processing, 2008, pp. 21–28. 14. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchenko A.A., Kutsaev A.S., Osipov A.S., Zakharov A.V. Affine Invariance Study of Edge Detection Algorithms by Means of PICASSO 2 System. Proc. 6th WSEAS Int. Conf. on Signal, Speech and Image Processing, 2006, pp. 11–16. 15. Грибков И.В., Захаров А.В., Кольцов П.П., Коганов М.А., Котович Н.В., Кравченко А.А., Куцаев А.С., Осипов А.С., Хисамбеев И.Ш. Развитие системы стохастического тестирования микропроцессоров INTEG // Программные продукты и системы. 2010. № 2. С. 14–23. References 1. Arabov I.I., Zakharov A.V., Koltsov P.P., Kotovich N.V., Kravchenko A.A., Koutsaev A.S., Nikolaev V.K., Pavlovskaya E.Ya. Realizatsiya i issledovanie prostranstvennogo izobrazheniya v realnom vremeni [Real-time implementation and study of the spatial image]. Moscow, NIISI RAN Publ., 1994, 14 p. 2. Gribkov I.V., Zakharov A.V., Koltsov P.P., Koto- vich N.V., Kravchenko A.A., Koutsaev A.S., Nikolaev V.K. Automated system of ground surface monitoring DEDAL-2. Integralnaya geometriya. Matematicheskie modeli. Ponimanie izobrazheny [Integral geometry. Mathematical models. Images Understanding]. Moscow, NIISI RAN Publ., 2001, pp. 5–50 (in Russ.). 3. Gribkov I., Koltsov P., Kotovich N., Kravchenko A., Koganov A., Kutsaev A., Nikolaev V., Zakharov A. PRIZM: Generator of Image Understanding Systems. Pattern Recognition and Image Analysis. 2000, vol. 10, no. 1, pp. 143–149. 4. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchen- ko A.A., Koutsaev A.S., Nikolaev V.K., Zakharov A.V. PICASSO – A system for evaluating edge detection algorithms. Pattern Recognition and Image Analysis. 2003, vol. 13, no. 4, pp. 617–622. 5. Gribkov I.V., Koltsov P.P, Kotovich N.V., Kravchen- ko A.A., Koutsaev A.S., Nikolaev V.K., Zakharov A.V. Testing of Energy Minimizing Methods in Image Preprocessing Using the PICASSO System. Proc. 8th World MultiConf. on Systemics, Cybernetics and Informatics. 2004, vol. 6, pp. 233–238. 6. Isard M., Blake A. Active Contours: The Application of Techniques from Graphics, Vision, Control Theory and Statistics to Visual Tracking of Shapes in Motion. Springer, 2000, 352 p. 7. Kass M., Witkin A., Terzopoulos D. Snakes: Active Contour Models. International Journal of Computer Vision, 1988, vol. 1, no. 4, pp. 321–331. 8. Xu Ch., Prince J.L. Shapes and Gradient Vector Flow. IEEE Transactions on Image Processing, 1998, vol. 7, no. 3, pp. 359–369. 9. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchen- ko A.A., Koutsaev A.S., Osipov A.S., Zakharov A.V. Study of Noisy and Blurry Images Segmentation. Proc. 9th int. conf. on Pattern Recognition and Image Analysis: New Information Technologies (PRIA-9-2008), 2008, vol. 1, pp. 193–196. 10. Pal S.K., Madjumadar D.D. Fuzzy Mathematical Approach to Pattern Recognition. NY, Wiley, 1986, 280 p. 11. Jäger G., Benz U. Measures of Classification Accuracy Based on Fuzzy Similarity. IEEE Trans. on Geoscience and Remote Sensing, 2000, vol. 38, no. 3, pp. 1462–1467. 12. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchen- ko A.A., Koutsaev A.S., Osipov A.S., Zakharov A.V. Performance evaluation of Texture Segmentation Methods. Proc. 13th World multiconf. on Systemics, Cybernetics and Informatics, 2009, vol. 4, pp. 137–142. 13. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchenko A.A., Koutsaev A.S., Osipov A.S., Zakharov A.V. Proc. 8th WSEAS Int. Conf. on Signal, Speech and Image Processing. 2008, pp. 21–28. 14. Gribkov I.V., Koltsov P.P., Kotovich N.V., Kravchen- ko A.A., Kutsaev A.S., Osipov A.S., Zakharov A.V. Proc. 6th WSEAS Int. Conf. on Signal, Speech and Image Processing. 2006, pp. 11–16. 15. Gribkov I.V., Zakharov A.V. Koltsov P.P., Koganov M.A., Kotovich N.V., Kravchenko A.A., Koutsaev A.S., Osipov A.S., Khisambeev I.Sh. The development of the system for microprocessor random testing INTEG. Programmnye produkty i sistemy [Software & Systems]. 2010, no. 2, pp. 14–23. | ||||||||||||||||||||||||||
http://swsys.ru/index.php?id=3651&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Интерактивное байесовское матирование изображений
- Исследование методов сегментации изображений
- Прогнозирование времени обработки изображений детерминированными методами
- Метод автоматического трекинга стволовых клеток по данным магнитно-резонансной томографии
- Методы обработки данных магнитно-резонансной томографии для когнитивной визуализации и трекинга областей интереса

 Эталонные изображения должны содержать максимально полный набор элементов изображения, являющихся типовыми для задачи, решаемой рассматриваемыми методами обработки видеографической информации.
Эталонные изображения должны содержать максимально полный набор элементов изображения, являющихся типовыми для задачи, решаемой рассматриваемыми методами обработки видеографической информации. я решения задачи выделения границ. Эти факторы имеют место в рассматриваемых эталонных изображениях. Вместе с тем описанные ситуации являются вполне типичными для естественных изображений. Кроме того, приведенные выше эталонные изображения можно довольно просто подвергать контролируемой деградации, внося аддитивный шум или размытие с известными параметрами.
я решения задачи выделения границ. Эти факторы имеют место в рассматриваемых эталонных изображениях. Вместе с тем описанные ситуации являются вполне типичными для естественных изображений. Кроме того, приведенные выше эталонные изображения можно довольно просто подвергать контролируемой деградации, внося аддитивный шум или размытие с известными параметрами. Для решения задачи выделения границ были рассмотрены программы, реализующие широко известные методы, названные по именам их авторов: Canny, Heitger, Rotwell, Black, Iverson, Smith [4]. Приведем примеры полученных оценок качества работы данных программ, реализующих эти методы, на эталонных изображениях. В качестве меры отличия результатов обработки изображений от ground truth были взяты статистические меры чувствительность (Se) и специфичность (Sp):
Для решения задачи выделения границ были рассмотрены программы, реализующие широко известные методы, названные по именам их авторов: Canny, Heitger, Rotwell, Black, Iverson, Smith [4]. Приведем примеры полученных оценок качества работы данных программ, реализующих эти методы, на эталонных изображениях. В качестве меры отличия результатов обработки изображений от ground truth были взяты статистические меры чувствительность (Se) и специфичность (Sp): 
 , где A – пикселы границы ground truth, то есть идеальная граница; B – пикселы границы, полученные в результате работы программы. На рисунке 4 приведены оценки, полученные при обработке эталонного изображения исчезающий уступ. По оси абсцисс отложена дисперсия белого шума, добавляемого к изображению, по оси ординат – чувствительность и специфичность (в процентах).
, где A – пикселы границы ground truth, то есть идеальная граница; B – пикселы границы, полученные в результате работы программы. На рисунке 4 приведены оценки, полученные при обработке эталонного изображения исчезающий уступ. По оси абсцисс отложена дисперсия белого шума, добавляемого к изображению, по оси ординат – чувствительность и специфичность (в процентах). ах описываемого подхода к оценке качества решения задачи обработки изображений были рассмотрены программные реализации часто используемых энергетических методов Мамфорда–Шаха, Гемана–Рейнольдса и метода с кусочно-линейной функцией [5], решающих задачу реставрации. Мера отличия результатов обработки изображений от ground truth находилась в метрике Евклида. Пример результатов, полученных при исследовании этих реализаций, приведен на рисунке 5. В качестве эталонного изображения взят изменяющийся горб II, имеющий границу с изменяющимся контрастом. В левой части рисунка приведен пример эталонного изображения, подвергнутого аддитивному гауссову зашумлению с вариацией, равной 30. В правой части по оси абсцисс отложены значения вариации гауссова зашумления от 0
ах описываемого подхода к оценке качества решения задачи обработки изображений были рассмотрены программные реализации часто используемых энергетических методов Мамфорда–Шаха, Гемана–Рейнольдса и метода с кусочно-линейной функцией [5], решающих задачу реставрации. Мера отличия результатов обработки изображений от ground truth находилась в метрике Евклида. Пример результатов, полученных при исследовании этих реализаций, приведен на рисунке 5. В качестве эталонного изображения взят изменяющийся горб II, имеющий границу с изменяющимся контрастом. В левой части рисунка приведен пример эталонного изображения, подвергнутого аддитивному гауссову зашумлению с вариацией, равной 30. В правой части по оси абсцисс отложены значения вариации гауссова зашумления от 0  до 30. По оси ординат – значения расстояния между ground truth и результатом работы трех программ. Пунктирная линия отображает ожидаемую линейную связь между вариацией шума и евклидовым расстоянием между защумленным и незашумленным эталонными изображениями. Угол в 45° для этой линии определяется выбором удобной нормировки.
до 30. По оси ординат – значения расстояния между ground truth и результатом работы трех программ. Пунктирная линия отображает ожидаемую линейную связь между вариацией шума и евклидовым расстоянием между защумленным и незашумленным эталонными изображениями. Угол в 45° для этой линии определяется выбором удобной нормировки.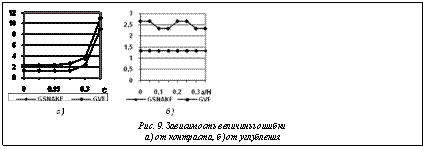 Уточнение контуров. В качестве примера использования описанного выше подхода к получению универсальной оценки качества работы программ обработки видеографической информации рассмотрим задачу уточнения контуров объекта. Эта задача обычно решается с помощью программ на основе так называемого метода активного контура [6], для реализаций которого трудными являются ситуации, когда контур объекта имеет большую кривизну. Поэтому в набор эталонных изображений для оценки качества работы соответствующих программ уточнения контуров были включены контуры с широким диапазоном изменений кривизны. На рисунке 6 приведен пример набора объектов на основе окружности, на рисунке 7 показаны два типа контуров, построенных с использованием квадрата и окружности. Следует отметить, что типичной ситуацией, влияющей на результаты работы программ, решающих задачу уточнения контуров объектов, является сложность фона. Поэтому к набору эталонных контуров добавляются и образцы фона. В таком случае эталонные изображения состоят из фона и наложенных на него границ объектов. Примеры использованных фонов показаны на рисунке 8.
Уточнение контуров. В качестве примера использования описанного выше подхода к получению универсальной оценки качества работы программ обработки видеографической информации рассмотрим задачу уточнения контуров объекта. Эта задача обычно решается с помощью программ на основе так называемого метода активного контура [6], для реализаций которого трудными являются ситуации, когда контур объекта имеет большую кривизну. Поэтому в набор эталонных изображений для оценки качества работы соответствующих программ уточнения контуров были включены контуры с широким диапазоном изменений кривизны. На рисунке 6 приведен пример набора объектов на основе окружности, на рисунке 7 показаны два типа контуров, построенных с использованием квадрата и окружности. Следует отметить, что типичной ситуацией, влияющей на результаты работы программ, решающих задачу уточнения контуров объектов, является сложность фона. Поэтому к набору эталонных контуров добавляются и образцы фона. В таком случае эталонные изображения состоят из фона и наложенных на него границ объектов. Примеры использованных фонов показаны на рисунке 8. В качестве программных реализаций метода активного контура взяты GSNAKE и GVF [7, 8], а в качестве меры ошибки решения – хаусдорфово расстояние в пикселах между результирующим и истинным контурами. На рисунке 9а показана зависимость С этой ошибки от нормализованного контраста фона и объектов для левого эталонного изображения на рисунке 7 (С=Dфон/(Mфон–Mобъект), где D – дисперсия, M – среднее). Обе реализации близки по качеству работы и с ростом С начинают выбирать ложные границы. На рисунке 9б представлена зависимость ошибки от относительной величины углубления a/H – отношение величины углубления a к величине объекта H – для эталонных изображений на рисунке 6 при С=0,225. Видно, что метод GVF дает лучшие результаты при любой величине углубления.
В качестве программных реализаций метода активного контура взяты GSNAKE и GVF [7, 8], а в качестве меры ошибки решения – хаусдорфово расстояние в пикселах между результирующим и истинным контурами. На рисунке 9а показана зависимость С этой ошибки от нормализованного контраста фона и объектов для левого эталонного изображения на рисунке 7 (С=Dфон/(Mфон–Mобъект), где D – дисперсия, M – среднее). Обе реализации близки по качеству работы и с ростом С начинают выбирать ложные границы. На рисунке 9б представлена зависимость ошибки от относительной величины углубления a/H – отношение величины углубления a к величине объекта H – для эталонных изображений на рисунке 6 при С=0,225. Видно, что метод GVF дает лучшие результаты при любой величине углубления. Как видим, поворот эталона на 45° существенно ухудшает качество работы программной реализации метода Smith. Особенно четко это демонстрирует метрика Хаусдорфа, обладающая высокой чувствительностью к различиям между сравниваемыми множествами. Изучение поведения всех ранее упомянутых программных реализаций методов выделения границ не выявило среди них абсолютного лидера.
Как видим, поворот эталона на 45° существенно ухудшает качество работы программной реализации метода Smith. Особенно четко это демонстрирует метрика Хаусдорфа, обладающая высокой чувствительностью к различиям между сравниваемыми множествами. Изучение поведения всех ранее упомянутых программных реализаций методов выделения границ не выявило среди них абсолютного лидера.
 Обрабатываемые изображения обычно имеют слабый контраст между яркостью и фоном. Это обстоятельство обусловило расширение набора эталонных изображений. Примеры таких изображений приведены на рисунке 12.
Обрабатываемые изображения обычно имеют слабый контраст между яркостью и фоном. Это обстоятельство обусловило расширение набора эталонных изображений. Примеры таких изображений приведены на рисунке 12. нтатора JSEG, а при малых углах наоборот. Эти графики приведены для случая отсутствия деградации изображений.
нтатора JSEG, а при малых углах наоборот. Эти графики приведены для случая отсутствия деградации изображений. рик. Методы решения задач с помощью средств вычислительной техники часто базируются на выделении некоторых узловых точек для последующей связи их в границы объекта. Для выявления способности различных программ, выделяющих границы, улавливать такие узловые точки был разработан подход на основе нечеткого сходства [10] с использованием нечетких метрик и нечетких ground truth эталонных изображений. На рисунке 14 приведены эталонное изображение – темный квадрат размером 5´5 пикселов на светлом фоне и результаты применения к нему программных реализаций Canny и Rothwell.
рик. Методы решения задач с помощью средств вычислительной техники часто базируются на выделении некоторых узловых точек для последующей связи их в границы объекта. Для выявления способности различных программ, выделяющих границы, улавливать такие узловые точки был разработан подход на основе нечеткого сходства [10] с использованием нечетких метрик и нечетких ground truth эталонных изображений. На рисунке 14 приведены эталонное изображение – темный квадрат размером 5´5 пикселов на светлом фоне и результаты применения к нему программных реализаций Canny и Rothwell. Как и в
Как и в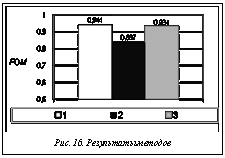 случае обычных эталонных изображений, выбор нечеткого эталонного изображения является неформальной задачей. Поскольку использование нечеткой метрики основывается на функции принадлежности, определяющей в данном случае степень истинности факта принадлежности пиксела к границе, для превращения эталонных изоб
случае обычных эталонных изображений, выбор нечеткого эталонного изображения является неформальной задачей. Поскольку использование нечеткой метрики основывается на функции принадлежности, определяющей в данном случае степень истинности факта принадлежности пиксела к границе, для превращения эталонных изоб ,
, ,
, ,
,