Оптические свойства тонких слоев металлов обусловливают их применение в самых различных устройствах: от зеркал и сверхчувствительных сенсоров [1], позволяющих регистрировать изменения показателя преломления порядка 10-7 [2], до оптических затворов и систем обработки информации [3]. Принято считать, что эти свойства весьма устойчивы к внешним воздействиям и только при переходе от макроскопических образцов к наноразмерам обнаруживается изменение спектра поглощения. Последний эффект связан с коллективными колебаниями электронов (так называемыми плазмoнными колебаниями) в наночастицах с размерами, меньшими длины свободного пробега электронов в массивных образцах. За- мечено, что статическая поляризуемость метал- лических кластеров, определяющая частоту коллективных колебаний, сильно отличается от макроскопической поляризуемости для кластеров, содержащих несколько десятков атомов [4]. Кроме того, расчеты показывают, что в кластерах Ag диаметром в 1–2 нм дополнительные 1–3 заряда электрона должны вызвать сдвиг линии плазмонного поглощения примерно в 5 нм, а уже для кластеров диаметром в 10 нм этот сдвиг ничтожен [5]. Это можно понять, поскольку сдвиг обусловлен изменением плотности заряда, которое заметно в случае малых кластеров и ничтожно мало в случае больших. Вместе с тем известно, что плазмонные частоты существенно зависят от формы и размера наночастиц. Приведенные примеры говорят о том, что существенного изменения оптических свойств металлических наноразмерных образцов без изменения их геометрии добиться очень трудно.
В настоящей работе приводятся результаты экспериментов, однозначно указывающие на значительное изменение эффективной диэлектрической восприимчивости на оптической частоте пленок Ag в наноразмерной структуре металл-диэлектрик-металл (МДМ).
Методика эксперимента
 Электронно-лучевым нанесением слоев в высоком вакууме были изготовлены экспериментальные макеты плазмонных МДМ-структур на основе четырехслойных нанопокрытий Al2O3/Ag/ Al2O3/Ag. На рисунке 1 показана структура с толщиной слоев d=12/49/177/36 нм соответственно с определенными оптическими свойствами. При нанесении слоев использовалась относительно низкая (~150 °С ) температура кварцевой подложки. Такая технология позволяет уменьшить размеры кристаллитов осаждаемых слоев и толщину переходных слоев, хотя и несколько снижает плотность диэлектрика. Внешний слой Al2O3 (d=12 нм) служил защитой от окисления Ag. Дополнительные адгезионные подслои не применялись. Для возбуждения SPR использовался лазер с длиной волны l=632,8 нм. При этом такая структура одновременно представляла собой металлодиэлектрический плазмонный оптический волновод, в котором существуют два резонанса SPR при углах q1=43° и q2=56,3°.
Электронно-лучевым нанесением слоев в высоком вакууме были изготовлены экспериментальные макеты плазмонных МДМ-структур на основе четырехслойных нанопокрытий Al2O3/Ag/ Al2O3/Ag. На рисунке 1 показана структура с толщиной слоев d=12/49/177/36 нм соответственно с определенными оптическими свойствами. При нанесении слоев использовалась относительно низкая (~150 °С ) температура кварцевой подложки. Такая технология позволяет уменьшить размеры кристаллитов осаждаемых слоев и толщину переходных слоев, хотя и несколько снижает плотность диэлектрика. Внешний слой Al2O3 (d=12 нм) служил защитой от окисления Ag. Дополнительные адгезионные подслои не применялись. Для возбуждения SPR использовался лазер с длиной волны l=632,8 нм. При этом такая структура одновременно представляла собой металлодиэлектрический плазмонный оптический волновод, в котором существуют два резонанса SPR при углах q1=43° и q2=56,3°.
Слои наносились через маски так, что сформировалась структура тонкопленочного конденсатора. Диаметр внешнего электрода из Ag составлял 3 мм. К такому конденсатору прикладывалось постоянное электрическое поле. Устойчивость структур к электрическому пробою составляла до 30 V, что соответствует напряженности поля в слое диэлектрика до 1,7´106 V/см при диэлектрической проницаемости корунда e=10. Однако в ряде случаев наблюдались снижение пробивного напряжения и возрастание токов утечки структур при повышенной влажности окружающей среды.
В ходе эксперимента измерялся спектр SPR – угловой спектр отражения от изготовленной МДМ-структуры. Измерения проводились методом поверхностного плазмонного резонанса по схеме Крейчмана [6]. Для измерения угловой зависимости нарушенного полного отражения использовался автоматический q–2q гониометр с полуцилиндром и дополнительной цилиндрической оптикой, обеспечивающей плоский фронт волны на образце.

 Результаты эксперимента приведены на рисунке 2, где показано, как изменяется вид спектра отражения при изменении напряженности электрического поля от 0 до 30 V. Анализ кривых показывает, что при напряжении более 4 V происходит заметное изменение коэффициента отражения, которое при U³16 V достигает насыщения. Ширина резонансов с ростом U существенно возрастает, однако их угловое смещение относительно исходных значений q1=43° и q2=56,3° не происходит. Коэффициент отражения при этом сильно изменяется: при увеличении напряжения до значений U>20 V он уменьшается более чем в 4 раза вблизи первого резонанса (при qSPR=42,9°) и увеличивается более чем в 5 раз в области второго резонанса (при qSPR=55,8°). На рисунке 2 видно, что можно условно выделить три группы кривых: первая соответствует интервалу напряжений UÎ[0, 6] V, вторая и третья – интервалам UÎ[8, 16] V соответственно. Обоснование такой группировки дается в следующем разделе при анализе зависимости оптических параметров от напряжения. Кроме того, имеются две точки, в которых величина отражения не зависит от приложенного напряжения: R»11,6 % при qSPR=53,95° и R»11,8 % при qSPR=57,39° для любых U. Существование этих точек трудно объяснить, однако их можно использовать для проверки результатов: теоретические кривые тоже должны пересекаться в этих точках.
Результаты эксперимента приведены на рисунке 2, где показано, как изменяется вид спектра отражения при изменении напряженности электрического поля от 0 до 30 V. Анализ кривых показывает, что при напряжении более 4 V происходит заметное изменение коэффициента отражения, которое при U³16 V достигает насыщения. Ширина резонансов с ростом U существенно возрастает, однако их угловое смещение относительно исходных значений q1=43° и q2=56,3° не происходит. Коэффициент отражения при этом сильно изменяется: при увеличении напряжения до значений U>20 V он уменьшается более чем в 4 раза вблизи первого резонанса (при qSPR=42,9°) и увеличивается более чем в 5 раз в области второго резонанса (при qSPR=55,8°). На рисунке 2 видно, что можно условно выделить три группы кривых: первая соответствует интервалу напряжений UÎ[0, 6] V, вторая и третья – интервалам UÎ[8, 16] V соответственно. Обоснование такой группировки дается в следующем разделе при анализе зависимости оптических параметров от напряжения. Кроме того, имеются две точки, в которых величина отражения не зависит от приложенного напряжения: R»11,6 % при qSPR=53,95° и R»11,8 % при qSPR=57,39° для любых U. Существование этих точек трудно объяснить, однако их можно использовать для проверки результатов: теоретические кривые тоже должны пересекаться в этих точках.
Полученные кривые зависимости R=R(q) коэффициента отражения R от угла падения q позволили рассчитать оптические параметры всех слоев МДМ-структуры (значения оптической толщины, показатели преломления n и коэффициенты поглощения k) как функции приложенного напряжения UÎ[0, 30] V. При этом эффективные оптические параметры слоев структуры определялись по наилучшему соответствию экспериментальных и теоретических угловых зависимостей величины отражения.
Моделирование углового спектра отражения проводилось стандартным способом с использованием известных пакетов прикладных программ (методика подробно описана в [7, 8]). Причем в отсутствие напряжения в качестве начальных значений для теоретической модели использовались оптические константы Ag и Al2O3 из базы SOPRA и толщина слоев, измеренная в ходе изготовления МДМ-структуры. Затем значения толщины покрытий корректировались расчетом по наилучшему совпадению модельной кривой R=R(q) с экспериментальной зависимостью отражения и фиксировались для последующих расчетов.
Результаты моделирования при U=0 показаны на рисунке 3 и приведены в таблице 1.
Таблица 1
Исходные оптические параметры слоев (U=0)
|
Материал слоя
|
Коэффициент преломления n
|
Коэффициент поглощения k
|
Толщина слоя (нм)
|
|
Al2O3
|
1,659
|
0
|
12,02
|
|
Ag
|
0,136
|
4,011
|
49,20
|
|
Al2O3
|
1,659
|
0
|
177,36
|
|
Ag
|
0,136
|
4,011
|
36,46
|
|
Подложка
|
1,525
|
0
|
-
|
При расчете спектров отражения с приложением внешнего поля (U>0) значения толщины слоев считались фиксированными (табл. 1), а эффективные оптические параметры слоев Ag и Al2O3 (коэффициенты преломления n и коэффициенты поглощения k) варьировались до достижения наилучшего совпадения с экспериментальным спектром. Причем все параметры верхнего защитного слоя Al2O3 (d=12 нм) также фиксировались в соответствии с таблицей 1, поскольку электрическое поле в нем должно отсутствовать.
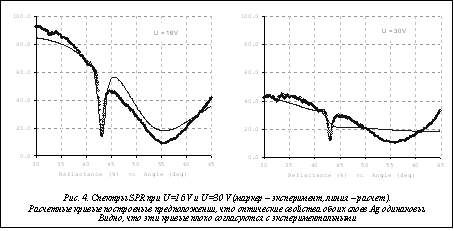
Сравнение экспериментальных и теоретических кривых позволяет сделать следующие выводы. Моделирование в отсутствие внешнего поля (рис. 3) близко к идеальному: исходные значения оптических параметров слоев при U=0 в точности соответствуют значениям, приведенным в оптической базе SOPRA. Моделирование при наличии напряжения требует большего внимания. Если принять, что оптические свойства обоих слоев Ag остаются одинаковыми при приложении электрического поля, то с увеличением напряженности будет наблюдаться все большее различие расчетных и экспериментальных данных, которое никак не устраняется вариацией величин n и k. Действительно, теоретические кривые на рисунке 4, построенные в этом предположении, очень плохо согласуются с экспериментальными. Очевидно, это вызвано тем, что при расчете не учитываются нелинейные эффекты, которые могут присутствовать при сильных напряженностях электрического поля, а также поверхностные заряды при поляризации диэлектрика и изменения плотности электронной плазмы в металлических слоях. Значительно лучшее соответствие теории и эксперимента достигается, если принять, что свойства Ag на катоде и аноде могут кардинально отличаться друг от друга.
Результаты моделирования
Если оптические параметры верхнего (анод) и нижнего (катод) слоев Ag различны, их оптимизацию следует проводить раздельно. Такое разделение возможно из предположений о накоплении зарядов на границах раздела диэлектрика и металла, а также изменений плотности электронной плазмы по толщине слоев металла в сильном электрическом поле.
Действительно, при толщине пленки диэлектрика d~200 нм и напряжении U~30 V поверхностная плотность заряда будет s=U/4ped0~40 CGSE (диэлектрическая проницаемость корунда e»10). Если площадь пленки равна 1 см2, то число избыточных электронов на одной из пленок Ag (и недостающих на другой) будет ~1011, в то время как полное число электронов проводимости будет ~1018.
 Выясним, к чему может привести дефицит заряда на пленке. Очевидно, что потенциальная яма для всех электронов анода окажется углубленной на 30 эВ. Но при этом надо учесть также изменение зонной структуры. Дело в том, что дополнительная сила притяжения со стороны нескомпенсированного положительного заряда приведет к сдвигу зоны проводимости и, конечно, уровня Ферми EF вниз по шкале энергий. Соответственно, это приведет к понижению порога межзонного поглощения. Зона d-электронов при этом сдвигается гораздо меньше из-за более сильной связи с ядром. Это можно понять, сравнивая данные по работе выхода А и порогу межзонного поглощения Δ для благородных металлов Ag, Au и Cu. Закономерность такова: чем ниже Δ, тем больше А. Объяснение очевидно: валентный электрон сильнее связывается с d-электронами, что и затрудняет его удаление из металла. Зона d-электронов при этом сдвигается гораздо меньше из-за более сильной связи с ядром.
Выясним, к чему может привести дефицит заряда на пленке. Очевидно, что потенциальная яма для всех электронов анода окажется углубленной на 30 эВ. Но при этом надо учесть также изменение зонной структуры. Дело в том, что дополнительная сила притяжения со стороны нескомпенсированного положительного заряда приведет к сдвигу зоны проводимости и, конечно, уровня Ферми EF вниз по шкале энергий. Соответственно, это приведет к понижению порога межзонного поглощения. Зона d-электронов при этом сдвигается гораздо меньше из-за более сильной связи с ядром. Это можно понять, сравнивая данные по работе выхода А и порогу межзонного поглощения Δ для благородных металлов Ag, Au и Cu. Закономерность такова: чем ниже Δ, тем больше А. Объяснение очевидно: валентный электрон сильнее связывается с d-электронами, что и затрудняет его удаление из металла. Зона d-электронов при этом сдвигается гораздо меньше из-за более сильной связи с ядром.
Изменение порога межзонного поглощения приводит к изменению диэлектрической проницаемости металла и, следовательно, параметров n и k. Например, для золота выведена модельная функция e(w) (см. [1]), которая учитывает два межзонных перехода, и с помощью одиннадцати подгоночных параметров (резонансные частоты, ширина резонансов, комплексные амплитуды, асимптотика и т.д.) удалось достичь хорошего совпадения с данными [9]. Для серебра до настоящего времени что-либо подобное не найдено, поэтому ограничимся приблизительной оценкой по формулам работы [1] для золота. Изменение порога Δ на 0,1 эВ приводит к изменению диэлектрической проницаемости примерно на единицу, что может быть обнаружно в экспериментах, аналогичных обсуждаемому.
В то же самое время на катоде избыток электронов приводит к повышению порога межзонного поглощения. Лишние электроны не вылетают из металла до тех пор, пока сила притяжения со стороны зарядов-изображений превышает силу отталкивания со стороны лишних электронов. Условие равенства этих сил можно записать в виде e2/l2=eU/2d, где U/2d – напряженность поля на катоде (в самом конденсаторе она вдвое больше), l – расстояние, на которое удаляется электрон от катода. Для напряжения насыщения получим Us=6×10–12/l2 V. Предположим, что медленные электроны рассеиваются дефектами, концентрация которых составляет ~1018 см-3, при этом средняя длина свободного пробега будет ~10 нм, и напряжение насыщения оказывается порядка нескольких вольт. При дальнейшем возрастании U наступает динамическое равновесие, то есть число электронов, поступающих в единицу времени на катод, равно числу электронов, в единицу времени просачивающихся через диэлектрик.
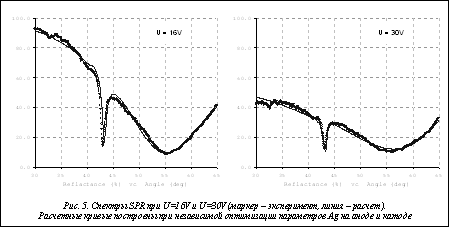 Таким образом, необходима независимая оптимизация оптических параметров верхнего (анод) и нижнего (катод) слоев Ag. Действительно, моделирование с независимой оптимизацией слоев анода и катода приводит к хорошему совпадению теоретических и экспериментальных кривых. На рисунке 5 приведены результаты моделирования углового спектра SPR при напряжениях U=16 V и U=30 V. Сравнение с кривыми рисунка 4 показывает, что независимая оптимизация приводит к существенному улучшению согласия теории с экспериментом. Расчетные величины оптических параметров, полученные при таком моделировании, приведены в таблице 2. Во-первых, обращает на себя внимание то, что показатель преломления анодного слоя оказался меньше, чем на катоде. Этот ожидаемый результат совпадает с измерениями, проводимыми в процессе изготовления структуры, и объясняется тем, что при напылении на гладкую подложку качество слоя серебра всегда выше, чем при напылении на относительно рыхлый промежуточный слой. Во-вторых, с ростом напряжения в слое диэлектрика Al2O3 появляется небольшое поглощение, а его показатель преломления уменьшается. Возможно, это связано с просачиванием электронов в этот слой из катода. Во избежание недоразумений следует подчеркнуть, что при моделировании невозможно учесть шероховатость поверхностей, взаимопроникновение слоев и нелинейные эффекты, которые могут присутствовать при сильных напряженностях электрического поля. Поэтому приведенные в таблице 2 значения параметров n и k следует рассматривать как некоторые эффективные значения, в какой-то мере учитывающие эти недостатки теоретического описания.
Таким образом, необходима независимая оптимизация оптических параметров верхнего (анод) и нижнего (катод) слоев Ag. Действительно, моделирование с независимой оптимизацией слоев анода и катода приводит к хорошему совпадению теоретических и экспериментальных кривых. На рисунке 5 приведены результаты моделирования углового спектра SPR при напряжениях U=16 V и U=30 V. Сравнение с кривыми рисунка 4 показывает, что независимая оптимизация приводит к существенному улучшению согласия теории с экспериментом. Расчетные величины оптических параметров, полученные при таком моделировании, приведены в таблице 2. Во-первых, обращает на себя внимание то, что показатель преломления анодного слоя оказался меньше, чем на катоде. Этот ожидаемый результат совпадает с измерениями, проводимыми в процессе изготовления структуры, и объясняется тем, что при напылении на гладкую подложку качество слоя серебра всегда выше, чем при напылении на относительно рыхлый промежуточный слой. Во-вторых, с ростом напряжения в слое диэлектрика Al2O3 появляется небольшое поглощение, а его показатель преломления уменьшается. Возможно, это связано с просачиванием электронов в этот слой из катода. Во избежание недоразумений следует подчеркнуть, что при моделировании невозможно учесть шероховатость поверхностей, взаимопроникновение слоев и нелинейные эффекты, которые могут присутствовать при сильных напряженностях электрического поля. Поэтому приведенные в таблице 2 значения параметров n и k следует рассматривать как некоторые эффективные значения, в какой-то мере учитывающие эти недостатки теоретического описания.
 Таблица 2
Таблица 2
Оптичеcкие параметры слоев МДМ-структуры
|
U, V
|
Ag (anode)
|
Al2O3
|
Ag (cathode)
|
|
n
|
k
|
n
|
k
|
n
|
k
|
|
0
|
0,1360
|
4,0110
|
1,6908
|
0,0000
|
0,1341
|
4,0100
|
|
4
|
0,1341
|
4,0109
|
1,6592
|
0,0022
|
0,1340
|
4,0100
|
|
8
|
0,5928
|
4,2967
|
1,6593
|
0,0087
|
0,0881
|
3,4853
|
|
12
|
0,5931
|
4,2969
|
1,6533
|
0,0116
|
0,0882
|
3,4852
|
|
16
|
0,5932
|
4,2970
|
1,6531
|
0,0113
|
0,0882
|
3,4852
|
|
20
|
0,3752
|
4,6909
|
1,5059
|
0,0583
|
0,0000
|
1,0263
|
|
24
|
0,3717
|
4,6840
|
1,5064
|
0,0589
|
0,0000
|
1,0308
|
|
28
|
0,3828
|
4,6885
|
1,5122
|
0,0622
|
0,0000
|
1,0619
|
|
30
|
0,3778
|
4,7022
|
1,5161
|
0,0642
|
0,0000
|
1,0816
|
Зависимость оптичеcких параметров слоев МДМ-структуры от напряжения показана на рисунке 6. Видно, что при напряжениях U~8 V и U~16 V все оптические параметры слоев Ag претерпевают резкие изменения. Аналогичное скачкообразное поведение наблюдается и у параметров диэлектрического слоя Al2O3. В промежутках между скачками величины n и k ведут себя достаточно стабильно у всех слоев. Исключение составляет только коэффициент поглощения диэлектрического слоя Al2O3, который демонстрирует небольшой рост на отрезке UÎ[20, 30] V. Интересно, что при напряжениях U~16 V показатель преломления катодного слоя Ag падает до нуля, то есть диэлектрическая проницаемость становится строго отрицательной без мнимой компоненты.
Следом за изменением величин n и k резко изменяется и коэффициент отражения. Наиболее сильные изменения в отражательной способности МДМ-структуры происходят при превышении напряжения U~16 V. Эксперимент на данной МДМ-структуре показал, что увеличение напряжения до значений U=20–30 V сопровождается уменьшением коэффициента отражения в 4,2 раза при qSPR=42,9° и увеличением его в 5,4 раза при qSPR=55,8°. Расчет показывает, что контрастность отражательной способности можно резко увеличить, незначительно варьируя толщину слоев. Например, увеличив толщину анодного слоя до 54 нм, получим структуру с нулевым отражением при угле падения qSPR=60,5°, коэффициент отражения которой поднимется до 20 % при повышении напряжения до U=30 V.
Таким образом, удалось обнаружить зна- чительное изменение диэлектрической прони- цаемости серебра под влиянием приложенного к оптической волноводной МДМ-наноструктуре постоянного напряжения до 30 V. Показано, что, изменяя напряжение, можно сильно модулировать величину коэффициента отражения. В перспективе данный эффект может быть использован при разработке электроуправляемых оптических ключей.
Получить приемлемое теоретическое обоснование скачкообразного изменения оптических параметров МДМ-структуры авторам пока не удалось. Это будет темой дальнейших исследований.
(Исследования проводились в рамках проектов №№ 1.8 и 2.1 Отделения нанотехнологий и информационных технологий РАН.)
Литература
1. Maier S. Plasmonics: Fundamentals and Applications, Springer, 2007.
2. Mikaelian A.L., Kryzhanovskiy B.V., Palagushkin A.N., Prokopenko S.A., Sergeev A.P., Yudkin F.A., Arlamenkov A.N. Sensors Using Plasmon Nanostructures, Optical Memory&Neural Network, 2005, vol. 14, pp. 229–238.
3. Cohen E., Dolev S., Kryzhanovskiy B., Palagushkin A., Frenkel S., Palagushkin A., Rosenblit M., Zakharov V. Optical solver of combinatorial problems: nanotechnological approach, JOSA A. 2013, vol. 30, iss. 9, pp. 1845–1853.
4. Knight W.D., Clemenger K., de Heer W.A., Saunders W.A. Phys. Rev. B, 1985, vol. 31, pp. 2539–2540.
5. Quinten M. Optical Properties of Nanoparticle Systems. Wiley-VCH Verlag & Co. KGaA. 2011.
6. Kretschmann E. Die Bestimmung optischer Konstanten von Metallen durch Anregung von Oberflachenplasmaschwingugen, Zeitschrift fűr Physic, 1971, Bd. 241, no. 4, pp. 313–324.
7. Palagushkin A.N., Prokopenko S.A., Sergeev A.P. Optical Memory and Neural Networks (Information Optics), 2007, vol. 16, pp. 288–294.
8. Palagushkin A.N., Prokopenko S.A., Sergeev A.P. Optical Memory and Neural Networks (Information Optics), 2009, vol. 18, pp. 156–163.
9. Etchegoin P.G., Le Ru E.C., Meyer M. Journ. of Chem, Physics, 2006, vol. 125, pp. 164–705.
References
1. Maier S. Plasmonics: Fundamentals and Applications. Springer, 2007.
2. Mikaelian A.L., Kryzhanovskiy B.V., Palagushkin A.N., Prokopenko S.A., Sergeev A.P., Yudkin F.A., Arlamenkov A.N. Sensors Using Plasmon Nanostructures. Optical Memory&Neural Network. 2005, vol. 14, pp. 229–238.
3. Cohen E., Dolev S., Kryzhanovskiy B., Palagushkin A., Frenkel S., Palagushkin A., Rosenblit M., Zakharov V. Optical solver of combinatorial problems: nanotechnological approach. JOSA A. 2013, vol. 30, iss. 9, pp. 1845–1853.
4. Knight W.D., Clemenger K., de Heer W.A., Saunders W.A. Phys. Rev. B. 1985, vol. 31, pp. 2539–2540.
5. Quinten M. Optical Properties of Nanoparticle Systems. Wiley-VCH Verlag & Co, KGaA, 2011, 502 p.
6. Kretschmann E. Determination of the metal optical constants through exciting surface plasma waves. Zeitschrift fűr Physik [Journ. of Physics]. 1971, vol. 241, no. 4, pp. 313–324 (in German).
7. Palagushkin A.N., Prokopenko S.A., Sergeev A.P. Optical Memory and Neural Networks (Information Optics). 2007, vol. 16, pp. 288–294.
8. Palagushkin A.N., Prokopenko S.A., Sergeev A.P. Optical Memory and Neural Networks (Information Optics). 2009, vol. 18, pp. 156–163.
9. Etchegoin P.G., Le Ru E.C., Meyer M. Journ. of Chem. Physics. 2006, vol. 125, pp. 164–705.




 Выясним, к чему может привести дефицит заряда на пленке. Очевидно, что потенциальная яма для всех электронов анода окажется углубленной на 30 эВ. Но при этом надо учесть также изменение зонной структуры. Дело в том, что дополнительная сила притяжения со стороны нескомпенсированного положительного заряда приведет к сдвигу зоны проводимости и, конечно, уровня Ферми EF вниз по шкале энергий. Соответственно, это приведет к понижению порога межзонного поглощения. Зона d-электронов при этом сдвигается гораздо меньше из-за более сильной связи с ядром. Это можно понять, сравнивая данные по работе выхода А и порогу межзонного поглощения Δ для благородных металлов Ag, Au и Cu. Закономерность такова: чем ниже Δ, тем больше А. Объяснение очевидно: валентный электрон сильнее связывается с d-электронами, что и затрудняет его удаление из металла. Зона d-электронов при этом сдвигается гораздо меньше из-за более сильной связи с ядром.
Выясним, к чему может привести дефицит заряда на пленке. Очевидно, что потенциальная яма для всех электронов анода окажется углубленной на 30 эВ. Но при этом надо учесть также изменение зонной структуры. Дело в том, что дополнительная сила притяжения со стороны нескомпенсированного положительного заряда приведет к сдвигу зоны проводимости и, конечно, уровня Ферми EF вниз по шкале энергий. Соответственно, это приведет к понижению порога межзонного поглощения. Зона d-электронов при этом сдвигается гораздо меньше из-за более сильной связи с ядром. Это можно понять, сравнивая данные по работе выхода А и порогу межзонного поглощения Δ для благородных металлов Ag, Au и Cu. Закономерность такова: чем ниже Δ, тем больше А. Объяснение очевидно: валентный электрон сильнее связывается с d-электронами, что и затрудняет его удаление из металла. Зона d-электронов при этом сдвигается гораздо меньше из-за более сильной связи с ядром. Таким образом, необходима независимая оптимизация оптических параметров верхнего (анод) и нижнего (катод) слоев Ag. Действительно, моделирование с независимой оптимизацией слоев анода и катода приводит к хорошему совпадению теоретических и экспериментальных кривых. На рисунке 5 приведены результаты моделирования углового спектра SPR при напряжениях U=16 V и U=30 V. Сравнение с кривыми рисунка 4 показывает, что независимая оптимизация приводит к существенному улучшению согласия теории с экспериментом. Расчетные величины оптических параметров, полученные при таком моделировании, приведены в таблице 2. Во-первых, обращает на себя внимание то, что показатель преломления анодного слоя оказался меньше, чем на катоде. Этот ожидаемый результат совпадает с измерениями, проводимыми в процессе изготовления структуры, и объясняется тем, что при напылении на гладкую подложку качество слоя серебра всегда выше, чем при напылении на относительно рыхлый промежуточный слой. Во-вторых, с ростом напряжения в слое диэлектрика Al2O3 появляется небольшое поглощение, а его показатель преломления уменьшается. Возможно, это связано с просачиванием электронов в этот слой из катода. Во избежание недоразумений следует подчеркнуть, что при моделировании невозможно учесть шероховатость поверхностей, взаимопроникновение слоев и нелинейные эффекты, которые могут присутствовать при сильных напряженностях электрического поля. Поэтому приведенные в таблице 2 значения параметров n и k следует рассматривать как некоторые эффективные значения, в какой-то мере учитывающие эти недостатки теоретического описания.
Таким образом, необходима независимая оптимизация оптических параметров верхнего (анод) и нижнего (катод) слоев Ag. Действительно, моделирование с независимой оптимизацией слоев анода и катода приводит к хорошему совпадению теоретических и экспериментальных кривых. На рисунке 5 приведены результаты моделирования углового спектра SPR при напряжениях U=16 V и U=30 V. Сравнение с кривыми рисунка 4 показывает, что независимая оптимизация приводит к существенному улучшению согласия теории с экспериментом. Расчетные величины оптических параметров, полученные при таком моделировании, приведены в таблице 2. Во-первых, обращает на себя внимание то, что показатель преломления анодного слоя оказался меньше, чем на катоде. Этот ожидаемый результат совпадает с измерениями, проводимыми в процессе изготовления структуры, и объясняется тем, что при напылении на гладкую подложку качество слоя серебра всегда выше, чем при напылении на относительно рыхлый промежуточный слой. Во-вторых, с ростом напряжения в слое диэлектрика Al2O3 появляется небольшое поглощение, а его показатель преломления уменьшается. Возможно, это связано с просачиванием электронов в этот слой из катода. Во избежание недоразумений следует подчеркнуть, что при моделировании невозможно учесть шероховатость поверхностей, взаимопроникновение слоев и нелинейные эффекты, которые могут присутствовать при сильных напряженностях электрического поля. Поэтому приведенные в таблице 2 значения параметров n и k следует рассматривать как некоторые эффективные значения, в какой-то мере учитывающие эти недостатки теоретического описания. Таблица 2
Таблица 2