Подготовка детализированной текстуры поверхности для высокореалистичной визуализации Земли
| Мальцев А.В. (avmaltcev@mail.ru) - НИИСИ РАН, г. Москва, г. Москва, Россия, кандидат физико-математических наук | |
| Ключевые слова: видеотренажеры, текстурирование, модели планет, высокореалистичная визуализация |
|
| Keywords: video trainers, texturing, planet models, high realistic visualization |
|
|
|
|
Важным требованием, предъявляемым к имитационно-тренажерным комплексам в различных научно-технических областях, является высокая реалистичность визуализируемых на компьютере трехмерных виртуальных моделей. В космических тренажерных системах к таким объектам относятся, например, Международная космическая станция (МКС), транспортные и грузовые корабли, Земля. Каждый из них играет существенную роль в правильном восприятии окружающей обстановки. Для обеспечения высокой реалистичности синтезируемых изображений Земли необходимо иметь детализированную текстуру ее поверхности. В данной статье рассматривается задача син- теза детализированной текстуры высокого разрешения для модели Земли, визуализируемой с использованием распределенных вычислительных систем и технологии сверхбольших текстур [1]. В качестве исходных данных берется набор тайлов – фотоизображений небольших участков земной поверхности. Все тайлы имеют одинаковый размер (в пикселах) и представлены в проекции Меркатора WGS84 (свойства данной проекции будут рассмотрены далее). Отметим, что обычно исходные наборы, как свободно распространяемые, так и доступные для коммерческого использования, не включают в себя крупные водные поверхности (озера, моря, океаны), что выражается в отсутствии тайлов, вообще не содержащих суши. В результате необходимо получить полную (то есть описывающую всю поверхность Земли) текстуру с эквидистантной цилиндрической проекцией. Для решения такой задачи в работе предлагаются алгоритм преобразования текстур высокого разрешения из проекции Меркатора в эквидистантную проекцию, а также технология бесшовного добавления в подготавливаемую текстуру отсутствующих в исходных данных водных поверхностей, обеспечивающая плавный переход между ними и сушей. Технология создания детализированной текстуры Земли Для решения задачи генерации детализированной текстуры Земли предлагается следующий алгоритм. На первом этапе необходимо осуществить сборку имеющихся тайлов в единое изображение M высокого разрешения. При этом участки водной поверхности, для которых отсутствуют тайлы, заполним черным цветом. Для хранения и обработки текстуры М применим формат данных Photoshop RAW 24 бит/пиксел (по 8 бит на каждую из цветовых компонент R, G, B). Исходные изображения, а значит и текстура М, представлены в проекции Меркатора [2] – равноугольной картографической проекции, сохраняющей углы между направлениями. Меридианы в ней обозначаются параллельными равноотстоящими линиями, а параллели – параллельными линиями, расстояние между которыми увеличивается при движении от экватора к полюсам. В связи с тем, что формула отображения координат на эллипсоиде в координаты на плоскости содержит функцию тангенса, аргумент которой при приближении к полюсам стремится к π/2, сами полюсы не могут быть представлены на проекции Меркатора. Поэтому обычно такую карту ограничивают областями до 80–85° северной и южной широты. Масштаб на карте Меркатора не является постоянным, он увеличивается от экватора к полюсам (как обратный косинус широты). Для применения создаваемой текстуры при визуализации модели Земли удобно использовать другой вид проекции – эквидистантную цилиндрическую [2]. Она является равнопромежуточной, то есть и меридианы, и параллели представляют собой равноудаленные прямые линии, а масштаб сохраняется при движении от экватора к полюсам. В отличие от проекции Меркатора данная проекция охватывает широтный интервал от 90° северной до 90° южной широты, а значит, включает полюсы. Для преобразования имеющейся текстуры М с проекцией Меркатора в текстуру E с эквидистантной цилиндрической проекцией в данной статье предлагается специальный алгоритм. На втором этапе необходимо подготовить дополнительную текстуру T (такого же размера в пикселах, что и E), на основе которой будут добавляться водные поверхности к созданной текстуре Е. T является модифицированным вари- антом так называемой текстуры маски земной поверхности, в которой белым цветом (1,0 в числовом эквиваленте) отображается суша, а черным (0,0) – водные поверхности. Использование черно-белого варианта маски отразилось бы в ярко выраженных границах между сушей в текстуре E и добавленными к ней водными поверхностями. Чтобы избежать резких цветовых границ и получить сглаженные переходы от суши к воде, в данной работе предлагается применять маску T в градациях серого цвета (в отрезке [0,0, 1,0]). Метод ее получения из исходного черно-белого изображения описан далее.
где Ei,j – исходный цвет рассматриваемого пиксела; Ti,j – числовой эквивалент цвета соответствующего пиксела маски; Cw – цвет водной поверхности. Цвет Cw может быть задан постоянной величиной или браться из соответствующего пиксела дополнительной, менее детальной, но полной текстуры земной поверхности (в той же цилиндрической проекции), приведенной к эквивалентному Е размеру в пикселах. Добавление водных поверхностей осуществляется практически без швов и обеспечивает возможность сохранения цвета прибрежного шельфа, если он имеется в исходном наборе тайлов. Таким образом, приходим к следующей технологии создания текстуры земной поверхности. I. Подготовка детализированной текстуры Земли без водных поверхностей: – сборка исходных тайлов в текстуру M; – преобразование М из проекции Меркатора в эквидистантную цилиндрическую проекцию с получением новой текстуры E. II. Подготовка текстуры маски: – приведение исходной черно-белой текстуры T ' маски к размеру E; – модификация T ' с получением маски в градациях серого, размывающей резкую цветовую границу между прибрежным шельфом в текстуре Е и добавляемой к ней водной поверхностью. III. Добавление водных поверхностей с учетом подготовленной маски. Рассмотрим подробнее алгоритм преобразования текстуры с проекцией Меркатора в текстуру с эквидистантной цилиндрической проекцией, а также метод создания необходимой текстуры T маски в градациях серого цвета (рис. 1). Преобразование проекции Пусть М (рис. 1а) – текстура земной поверхности с проекцией Меркатора, имеющая размер Wm´Hm пикселов (Wm и Hm кратны 2); Xm и Ym – оси системы координат Меркатора; Im и Jm – оси системы координат для индексирования пикселов из M. Начальные точки обеих систем совпадают и находятся в середине карты M. Кроме того, пусть результирующая текстура E с эквидистантной цилиндрической проекцией (рис. 1б) имеет размер We ´He пикселов, Xe и Ye – оси широтно-долготной системы координат, Ie и Je – оси системы координат для индексирования пикселов из E. Начальные точки этих систем также совпадают и располагаются в центре текстуры E. Отметим, что для эквидистантной цилиндрической проекции характерно соотношение 2:1 ширины и высоты карты [2], то есть He=We/2. Чтобы при преобразовании сохранить исходное разрешение текстуры по оси абсцисс, возьмем We = Wm. Предположим, что имеющаяся текстура M создана с учетом эллипсоидной формы Земли. Поэтому для преобразования проекции возьмем за основу формулы перевода широты φ и долготы λ для эквидистантной цилиндрической проекции в координаты xm и ym карты Меркатора для эллипсоида [2, 3]: xm=al,
где Введем коэффициент масштабирования ρm для пересчета непрерывных координат ym карты Меркатора в дискретные координаты jm пикселов имеющейся у нас текстуры земной поверхности в проекции Меркатора:
где скобки обозначают целую часть числа. Аналогично пусть коэффициент масштабирования ρe для пересчета непрерывных широтных координат (в радианах) в дискретные координаты jе пикселов текстуры земной поверхности в эквидистантной цилиндрической проекции равен
Поскольку, как упоминалось ранее, представленные в карте Меркатора максимальная φmax и минимальная φmin широты составляют не более 85° северной и южной широты соответственно, при преобразовании проекции текстура M отобразится только в центральную область U (с индексами jeÎ[je,min, je,max]) текстуры E, содержащей широты φÎ[-90°, 90°] (рис. 2). Используя формулу (3), получим Области текстуры E, лежащие за пределами U, закрасим в черный цвет. Они будут обработаны в дальнейшем на этапе добавления водных поверхностей. Для формирования области U необходимо определить соответствие ее пикселов пикселам текстуры M. Поскольку и карта Меркатора, и эквидистантная проекция охватывают долготный диапазон [-π, π], We=Wm, а масштаб карты Меркатора по оси Y растет от экватора к полюсам, каждому пикселу (ie, je)ÎU соответствует отрезок R из некоторого числа r пикселов (im, jm,k)ÎМ, где im=ie и kÎ[0, r–1] (рис. 2). Чтобы определить границы jm,0 и jm,r-1 этого отрезка, используем формулы (1)–(3). Сначала из равенства (3) найдем значения широт, соответствующих верхней и нижней границам рассматриваемого пиксела (ie, je) текстуры E: jtop=re(je+1), jbottom=re·je. Далее, подставляя их в формулу (1) и учитывая равенство (2), получим
Цвет пиксела (ie, je) текстуры E определим как среднее арифметическое цветов пикселов текстуры M, входящих в R:
Таким образом, рассмотрен следующий алгоритм преобразования текстуры из проекции Меркатора в эквидистантную цилиндрическую проекцию. · Определение области U (с индексами jeÎ[je,min, je,max]) текстуры E, на которую отображается текстура M. · Заполнение областей jeje,max черным цветом. · Для каждого пиксела (ie, je)ÎU: – определение соответствующего отрезка R из r пикселов текстуры M, – поиск границ R по формуле (4), – вычисление цвета пиксела (ie, je) по формуле (5). Создание текстуры маски Рассмотрим процедуру создания модифицированной текстуры T маски, необходимой для бесшовного добавления водных поверхностей, отсутствующих в подготовленной на предыдущем этапе текстуре E. Пусть T ' – исходная текстура маски в эквидистантной цилиндрической проекции. Белым цветом в ней отображается суша, а черным – водные поверхности. Для создания текстуры T необходимо осуществить размытие границ областей суши в пределах 0,0003–0,0005 % от большего из размеров текстуры T '. Чтобы береговая линия после слияния E и текстуры водной поверхности осталась четкой, размытие должно производиться непосредственно от границ белых областей в направлении черных. На рисунке 3 процесс размытия границ про- иллюстрирован на примере отдельного участка текстуры T '. Область размытия G для данного участка выделена пунктиром (рис. 3а). Половину данной области, прилежащую к суше, заполним серым цветом с числовым эквивалентом 0,5 (рис. 3б), после чего применим к G фильтр размытия по Гауссу. В результате использования фильтра получаем участок требуемой текстуры T (рис. 3в) – модифицированной маски.
Практическое использование описанных решений На базе предложенных в данной статье технологий и алгоритмов разработан программный комплекс, выполняющий синтез высокодетализированной текстуры земной поверхности (из набора тайлов в проекции Меркатора) для ее последующего использования при визуализации модели Земли в имитационно-тренажерных системах. Комплекс состоит из трех приложений: Map creator, Map converter, Map merger, работающих под управлением операционной системы Microsoft Windows, и одного сценария для программы Adobe Photoshop. Приложения ориентированы на решение подзадач, составляющих описанную технологию. Map creator отвечает за сборку текстуры высокого разрешения из набора тайлов формата BMP в несжатый RAW-файл, а также при необходимости за нарезку такой текстуры на тайлы (поддерживаются несколько форматов записи). Map converter обеспечивает преобразование текстуры в формате RAW из проекции Меркатора в эквидистантную цилиндрическую проекцию. Добавление водных поверхностей осуществляется с помощью Map merger. Сценарий, в свою очередь, обеспечивает возможность создания в Photoshop необходимой для Map merger текстуры маски. Данный п Таким образом, в данной статье предложены технология и алгоритмы создания высокодетализированной текстуры земной поверхности. Рассмотрены сборка текстуры из набора тайлов, преобразование текстуры с проекцией Меркатора в текстуру с эквидистантной цилиндрической проекцией, добавление отсутствующих в исходных данных водных поверхностей. На основе описанных подходов разработан программный комплекс из трех приложений и одного сценария для Adobe Photoshop, позволяющий готовить такую текстуру за несколько шагов. Литература 1. Тимохин П.Ю. Технология визуализации ландшафтов с использованием сверхбольших текстур // Гагаринские чтения: науч. тр. XXXIX Междунар. молодеж. науч. конф. М.: МАТИ, 2013. Т. 2. С. 130–131. 2. Osborne P. The Mercator projections, Edinburgh, 2013. URL: http://www.mercator99.webspace.virginmedia.com/mercator.pdf (дата обращения: 05.06.2013). 3. Evenden G.I. Libproj4: A Comprehensive Library of Cartographic Projection Functions. Falmouth, MA, USA, 2008. 4. Михайлюк М.В., Торгашев М.А. Система «GLView» визуализации для моделирующих комплексов и систем виртуальной реальности // Вестн. РАЕН. 2011. Т. 11. № 2. С. 20–28. References 1. Timokhin P.U. Tekhnologiya vizualizatsii landshaftov s ispolzovaniem sverkhbolshikh tekstur. Gagarinskie chteniya: Nauchnye trudy XXXIX Mezhdunar. molodezhnoy nauchnoy konf. [Gagarin readings: proc. of 39th youth scientific conf.]. Moscow, Russian State Technol. Univ. (MATI) Publ., 2013, vol. 2, pp. 130–131. 2. Osborne P. The Mercator projections. Edinburgh, 2008. Available at: http://www.mercator99.webspace.virginmedia.com/ mercator.pdf (accessed 5 June 2013). 3. Evenden G.I. Libproj4: A Comprehensive Library of Cartographic Projection Functions. Falmouth, MA, USA, 2008. 4. Mikhaylyuk M.V., Torgashev M.A. Visualisation system «GLView» for modeling complexes and virtual reality system. Vestnik RAEN [RANS bulletin]. 2011, vol. 11, no. 2, pp. 20–28.je,max черным цветом. · |
http://swsys.ru/index.php?id=3658&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:

 На третьем этапе выполняется добавление водных поверхностей к подготовленной на первом этапе детализированной текстуре E с использованием маски T. При этом новый цвет E'i,j пиксела (i, j) текстуры E вычисляется по формуле
На третьем этапе выполняется добавление водных поверхностей к подготовленной на первом этапе детализированной текстуре E с использованием маски T. При этом новый цвет E'i,j пиксела (i, j) текстуры E вычисляется по формуле ,
,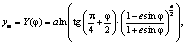 (1)
(1)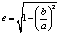 ; a и b – соответственно большая и малая полуоси земного эллипсоида (в рассматриваемой системе WGS84 a=6378137,0, b=6356752,3142).
; a и b – соответственно большая и малая полуоси земного эллипсоида (в рассматриваемой системе WGS84 a=6378137,0, b=6356752,3142).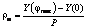 , где
, где 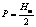 , jmax – географическая широта, соответствующая верхней строке пикселов (с координатой
, jmax – географическая широта, соответствующая верхней строке пикселов (с координатой 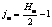 ) текстуры M (рис. 1а). Тогда, зная координату jm пиксела, легко найти для него ym, и наоборот:
) текстуры M (рис. 1а). Тогда, зная координату jm пиксела, легко найти для него ym, и наоборот: ,
,  , (2)
, (2)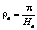 , тогда по значению широты φ можно вычислить координату jе :
, тогда по значению широты φ можно вычислить координату jе : . (3)
. (3) ,
, 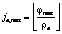 .
. ,
, 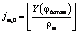 . (4)
. (4)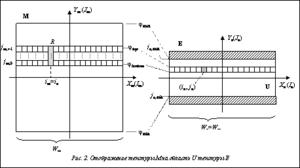
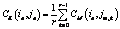 . (5)
. (5)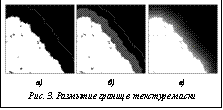 Указанные операции с текстурой удобно выполнять в графическом редакторе Adobe Photoshop, используя заранее подготовленный сценарий, описывающий необходимые действия.
Указанные операции с текстурой удобно выполнять в графическом редакторе Adobe Photoshop, используя заранее подготовленный сценарий, описывающий необходимые действия. рограммный комплекс апробирован при подготовке текстуры поверхности для модели Земли, разработанной в ЦВИСИТ НИИСИ РАН. На рисунке 4 представлено изображение, сгенерированное системой визуализации реального времени «GLView» [4], также созданной в ЦВИСИТ, в результате рендеринга моделей Земли и МКС.
рограммный комплекс апробирован при подготовке текстуры поверхности для модели Земли, разработанной в ЦВИСИТ НИИСИ РАН. На рисунке 4 представлено изображение, сгенерированное системой визуализации реального времени «GLView» [4], также созданной в ЦВИСИТ, в результате рендеринга моделей Земли и МКС.