Моделирование процессов упругопластического деформирования модифицированным методом граничных элементов
| Федотов В.П. (fedotov@imach.uran.ru) - Московский государственный технический университет им. Н.Э. Баумана, г. Москва, Россия, Спевак Л.Ф. (lfs@imach.uran.ru) - Институт машиноведения УрО РАН, г. Екатеринбург, г. Екатеринбург, Россия, доктор технических наук, Нефедова О.А. (nefedova@imach.uran.ru) - Институт машиноведения УрО РАН, г. Екатеринбург, г. Екатеринбург, Россия | |
| Ключевые слова: упругопластические деформации, аналитическое интегрирование, модифицированный метод граничных элементов, параллельные вычисления |
|
| Keywords: elastic-plastic deformations, analytical integration, modified boundary element method, parallel computing |
|
|
|
|
Расчет напряженно-деформированного состояния в элементах конструкций является базой для оценки их надежности и долговечности. Наибольшее значение имеет исследование поведения находящейся под нагрузками среды в случае возможного появления необратимых пластических деформаций. В связи с этим разработка эффективных средств решения статических задач упругопластического деформирования является важной и актуальной задачей. Применение модифицированного метода граничных элементов (ММГЭ) для решения как линейных, так и нелинейных задач математической физики показало высокую эффективность разработанного авторами подхода [1]. Создание на его основе алгоритма и высокопроизводительного программного средства для решения двухмерных задач упругопластического деформирования – логичное и естественное распространение подхода на новую область. Основой разрабатываемых граничноэлементных алгоритмов является аналитическое вычисление граничных интегралов по полученным авторами формулам. Кроме этого, в сами алгоритмы заложено распараллеливание вычислений. Решение нелинейной задачи упругопластического деформирования производится итерационно. На каждой итерации решается неоднородная линейная задача теории упругости, при этом неоднородная часть содержит расчетные данные с предыдущего итерационного шага. Таким образом, все преимущества решения МГЭ линейных задач переносятся на случай нелинейной задачи. Краевая задача упругопластического деформирования Система уравнений краевой задачи в рамках теории малых упругопластических деформаций для двухмерной области Ω состоит из уравнений равновесия, записанных в компонентах тензора напряжений σij, соотношений Коши, записанных для компонент тензора деформаций εij, определяющих соотношений, характеризующих свойства материала, и граничных условий: σij, j=0, (1)
u=u* на Su; σij nj=fi= fi* на Sf. (4) Здесь ui – компоненты вектора перемещения; G=E/(2(1+ν)) – модуль упругости при сдвиге, E – модуль Юнга, ν – коэффициент Пуассона; δij – символ Кронекера; Алгоритм решения В формулировке с начальными напряжениями для любой внутренней точки xÎW справедливо
где uij*(ξ, x) и fij*(ξ, x) – известные функции влияния; Ωпл – область пластического течения [2, 3]. Граничное интегральное уравнение в этом случае имеет вид
где x0 – произвольная граничная точка. Итерационная процедура, основанная на соотношениях (5) и (6), которая применялась при расчете напряженно-деформированного состояния при неупругой деформации, может быть схематично описана следующим образом. 1. На первой итерации решается задача теории упругости в предположении, что σij0(x)=0. · Для некоторого разбиения границы S на граничные элементы уравнение (6) сводится к системе линейных уравнений, решение которой дает неизвестные значения ui(1) и fi(1) в граничных точках области Ω в первом приближении. · Во внутренних точках области Ω в соот- ветствии с формулой (5) и уравнением (2) по известным граничным значениям рассчитываются в первом приближении компоненты ui(1), εij(1). При расчетах используются аналитические формулы интегрирования, полученные ранее с использованием ММГЭ [2]. По формуле (3) вычисляются компоненты тензора напряжений σije(ε(1)), соответствующие упругим деформациям. · Из условия текучести T=τs определяются точки границы Sпл пластической зоны Ωпл облас- ти Ω. · Внутри пластической зоны Ωпл рассчитываются начальные напряжения σij0(ε(1)) в соответствии с уравнением (3). 2. На k-й итерации решается задача с учетом значений начальных напряжений σij0(ε(k-1)), полученных на предыдущем шаге. · Из граничного интегрального уравнения (5) определяются неизвестные значения ui(k) и fi(k) в граничных точках области Ω. Для вычисления интеграла по Ωпл пластическая область разбивается на конечные элементы. Значения σij0(ε(k-1)) предполагаются постоянными на каждом элементе и отнесенными к их серединам, тогда справедливы соотношения
Здесь Nпл – число конечных элементов em в области Ωпл; Sm – граница элемента em; nj – компоненты внешней нормали к границе Sm. · Во внутренних точках области Ω по известным граничным значениям рассчитываются ui(k), εij(k), σije(ε(k)). · · Внутри области Ωпл рассчитываются новые начальные напряжения σij0(ε(k)). 3. Расчет продолжается, пока две последующие итерации ui(k-1) и ui(k) не станут достаточно близки. Описание программы На основе представленного алгоритма была разработана программа для ЭВМ, выполняющая расчет напряженно-деформированного состояния для произвольной двухмерной области, подверженной упругопластическому деформированию. Основная цель создания программы заключалась в том, чтобы с привлечением технологий параллельного вычисления максимально ускорить счет, а использованием в алгоритме ММГЭ повысить точность расчетов. Блок-схема программы представлена на рисунке 1. Программа имеет простой и удобный в использовании интерфейс. Графический редактор написан на языке программирования Java. С помощью возможностей графического редактора можно построить произвольную плоскую область, аппроксимируя ее границу отрезками прямых или дуг окружности. Для целостного восприятия задачи экран ввода данных состоит из пяти окон. Первое окно – «Модель области» – это система координат для моделирования деформируемой области. Четыре других окна – таблицы для ввода входных параметров задачи. В левой части экрана расположена таблица «Координаты граничных узлов», она содержит координаты граничных узлов прямолинейных и круговых участков границы. Справа вверху находится таблица «Расчетная область» с координатами узлов внутренней расчетной области. Под ней таблица с физическими параметрами процесса «Физические параметры». Внизу экрана расположена таблица «Граничные условия» с граничными условиями и количеством граничных элементов на каждом участке границы. Данные всех таблиц легко редактируются вручную. Можно перемещать таблицы по экрану, а также изменять их размеры. В левой верхней части экрана ввода размещены основные кнопки для работы с программой. С их помощью можно выполнять следующие действия: изменять масштаб координатной сетки, сохранять в файл геометрическую модель области и параметры задачи, открывать сохраненную ранее модель, очищать экран и таблицы параметров, отправлять задачу на счет, сохранять результаты расчета в файле Exсel. Выходные данные включают в себя компоненты вектора перемещения, тензора деформаций, тензора напряжений, а также инварианты тензора напряжений. Все величины рассчитаны для заданных внутренних точек области Ω. Использование таблицы Exсel позволяет наглядно представить полученные расчетные данные, построить графики на их основе, упрощает обработку и анализ результатов.
Пример При использовании программы была решена задача упругопластического деформирования прямоугольной пластины размером l×d c круговым отверстием радиуса a, подверженной растяжению. Предполагалось, что в области пластического течения компоненты девиатора напряжений связаны с компонентами девиатора деформаций зависимостью
Здесь
где начальные напряжения вычисляются по формуле В силу симметрии деформируемой области задача была решена для половины пластины при следующих значениях параметров: l=20 м; d=10 м; a=1 м; E=2·1011 Н/м2; ν=0,28; f=2·108 Н/м2; τs=2·108 Н/м2; p=2·108 Н/м2. После введения физических и геометрических характеристик задачи с помощью разработанного графического редактора экран ввода данных имеет вид, представленный на рисунке 2. Результаты решения по предложенному алгоритму сравнивались с данными, полученными в пакете ANSYS. На рисунке 3 выполнено сравнение графиков, описывающих изменение компоненты тензора напряжений σ22 вдоль оси Ox1. На основании изложенного можно сделать вывод о том, что построенный алгоритм и разработанная программа для расчета характеристик напряженно-деформированного состояния материала при упругопластическом деформировании двухмерной области показали свою эффективность. Использование ММГЭ позволило свести решение задачи в области W к решению на границе S и получать непрерывные деформации в любой точке рассматриваемой области. В области пластического течения учитывалось влияние пластической деформации на расчетные характеристики материала. Были снижены временные затраты на решение краевой задачи из-за возможности распараллеливания алгоритма. Литература 1. Федотов В.П., Спевак Л.Ф. Модифицированный метод граничных элементов в задачах механики, теплопроводности и диффузии. Екатеринбург: УрО РАН, 2009. 164 с. 2. Бенерджи П. Метод граничных элементов в прикладных науках. М.: Мир, 1984. 494 с. 3. Бреббия К., Теллес Ж., Вроубел Л. Метод граничных элементов. М.: Мир, 1987. 526 с. 4. Антонов А.C. Параллельное программирование с использованием технологии MPI. М.: МГУ, 2004. 71 с. References 1. Fedotov V.P., Spevak L.F. Modifitsirovanny metod granichnykh elementov v zadachakh mekhaniki, teploprovodnosti i diffuzii [A modified boundary element method in mechanics, transcalency and diffusion problems]. Ekaterinburg, Ural Branch of RAS Publ., 2009, 164 p. 2. Banerjee P.K., Butterfield R. A boundary element method in engineering science. McGraw-Hill Inc. Publ., 1981, 452 p. 3. Brebbia C.A., Telles J.C.F., Wrobel L.C. Boundary element techniques. Springer. Berlin, Heidelberg Publ., 1984, 526 p. 4. Antonov A.S. Parallelnoe programmirovanie s ispolzovaniem tekhnologii MPI [Parallel programming using MPI technology]. Moscow, MSU Publ., 2004, 71 p. |
http://swsys.ru/index.php?id=3696&lang=%E2%8C%A9%3Den&like=1&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Программный комплекс для решения задач теории потенциала методом граничных элементов
- Параллельные алгоритмы для анализа прочности наводороженных конструкций
- Параллельные вычисления при моделировании процесса растворения на микроуровне
- Исследование эффективности библиотеки MaLLBa на примере задач максимальной выполнимости
- Неоднозначная семантика и некорректности при работе с потоками на C#

 , (2)
, (2) (3)
(3) – интенсивность касательных напряжений, sij=σij–σkkδij/3 – ком- поненты девиатора напряжений; τs – предел текучести материала на сдвиг; σije(x) – напряжения, соответствующие упругим деформациям; σij0(x) – «начальные» напряжения, соответствующие неупругим деформациям; S=SuÈSf – граница области Ω; fi – компоненты вектора поверхностных напряжений; ni – компоненты вектора внешней нормали к границе; i, j=1,2, по повторяющемуся индексу производится суммирование; звездочкой отмечены известные функции. В задачу входит определение во внутренних точках области Ω компонент вектора перемещения, тензора деформаций и тензора напряжений.
– интенсивность касательных напряжений, sij=σij–σkkδij/3 – ком- поненты девиатора напряжений; τs – предел текучести материала на сдвиг; σije(x) – напряжения, соответствующие упругим деформациям; σij0(x) – «начальные» напряжения, соответствующие неупругим деформациям; S=SuÈSf – граница области Ω; fi – компоненты вектора поверхностных напряжений; ni – компоненты вектора внешней нормали к границе; i, j=1,2, по повторяющемуся индексу производится суммирование; звездочкой отмечены известные функции. В задачу входит определение во внутренних точках области Ω компонент вектора перемещения, тензора деформаций и тензора напряжений. (5)
(5) (6)
(6)

 Из условия текучести T=τs определяются новые точки границы Sпл.
Из условия текучести T=τs определяются новые точки границы Sпл.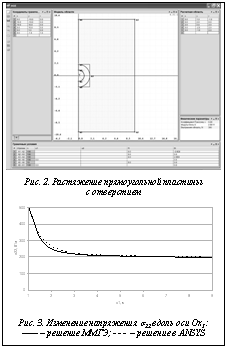 Расчетная часть программы написана на языке программирования С++ с использованием библиотеки MPI для распараллеливания [4]. Счет осуществлялся на кластере umt («Уран») Института математики и механики УрО РАН (г. Екатеринбург).
Расчетная часть программы написана на языке программирования С++ с использованием библиотеки MPI для распараллеливания [4]. Счет осуществлялся на кластере umt («Уран») Института математики и механики УрО РАН (г. Екатеринбург). , T=q+pГ. (7)
, T=q+pГ. (7) – интенсивность деформаций сдвига; eij=εij–εmmδij/3 – компоненты девиатора деформаций, значение параметра q определяется из условия непрерывности соотношений (3) при T=τs. После подстановки (7) соотношения (3) принимают вид
– интенсивность деформаций сдвига; eij=εij–εmmδij/3 – компоненты девиатора деформаций, значение параметра q определяется из условия непрерывности соотношений (3) при T=τs. После подстановки (7) соотношения (3) принимают вид
 .
.