Программные продукты и системы

Главное отличие процессов и процедур послепродажного сопровождения, принятых в России и описываемых в отечественных нормативных документах, от аналогичных процессов и процедур, регламентированных зарубежными стандартами, состоит в том, что отечественные документы не предусматривают систематическое применение информационных технологий для поддержки этих процессов. Проблема интегрированной логистической поддержки (ИЛП) приобрела особую актуальность в связи с выходом отечественных предприятий – производителей наукоемкой продукции – на международный рынок. Иностранные заказчики предъявляют к средствам и системам послепродажного сопровождения российских изделий те же требования, что и к аналогичным изделиям зарубежных фирм. В этой связи проблема организации ИЛП для изделий российских предприятий переходит в разряд первоочередных, поскольку от ее решения в значительной мере зависит конкурентоспособность отечественной машиностроительной продукции на мировом рынке. На рисунке 1 схематически показаны основные элементы ИЛП. Одной из составляющих является управление техническим обслуживанием и ремонтом (ТОиР).

В силу общеизвестных экономических причин (инфляция), с разной степенью интенсивности действующих практически во всех странах, приведенная стоимость изделия со временем возрастает, а приведенные эксплуатационные расходы убывают. На рисунке 2 представлен безразмерный график, иллюстрирующий указанные тенденции, стоимость жизненного цикла (СЖЦ) изделия.

Снижение эксплуатационных расходов позволит снизить расходы перевозчиков и тем самым повысить конкурентоспособность воздушных судов (ВС). Расходы на ТОиР являются наиболее предсказуемой и управляемой составляющей общих расходов на эксплуатацию, величина которой может колебаться от 10 до 50 % в зависимости от совершенства действующей системы технической эксплуатации. Основными параметрами, характеризующими совершенство системы ТОиР, являются объем и периодичность выполнения работ по техническому обслуживанию (ТО), оказывающие прямое влияние на эксплуатационные расходы и интенсивность эксплуатации ВС.

Основой любого управления, в том числе управления ТОиР, является планирование, определяющее цели управления, ресурсы, необходимые для достижения этих целей, а также действия по достижению целей и их распределение во времени. Поэтому в дальнейшем управление ТОиР исследуется в аспекте планирования. В работе будет рассмотрено управление ТО оборудования.

Все вышесказанное предопределяет актуальность тематики исследований, изложенных в статье. Поскольку управление ТОиР требует обработки больших объемов разнообразной информации, его выполнение возможно только в автоматизированном режиме, то есть по сути речь идет об автоматизации достаточно своеобразного технологического процесса инженерной деятельности.

Определение ТОиР

ТО – комплекс операций или операция по поддержке работоспособности и исправности изделия при использовании по назначению, ожидании, хранении и транспортировке (ГОСТ 18322-72).

Ремонт – комплекс операций по восстановлению исправности или работоспособности изделий и восстановлению ресурсов изделий или их составных частей (ГОСТ 18322-72).

К операциям ТОиР относятся устранение отказов оборудования, инспекция в определенном объеме с определенной периодичностью, плановая замена деталей и ремонт оборудования по состоянию, наработке, а также планирование ремонтов и обслуживания.

Выделяют следующие виды ТОиР: обслуживание по событию (например, устранение поломки оборудования); регламентное обслуживание (в паспорте производителя описано, в каком режиме и какое обслуживание необходимо выполнять для поддержания работоспособности оборудования); по состоянию (на основании оценки делается прогноз, когда оборудование надо выводить в ремонт).

ТОиР – сложный многофазный процесс, выполняемый силами заказчика (эксплуатанта), сервисной службы (подразделения), производителя. Работы выполняются на основе регламентов и тех­нологий при помощи специального оборудования, разрабатываемого и изготавливаемого по согласованным с заказчиком техническим требованиям.

Рассмотрим методы распределения работ для планирования ТО.

·       Поэтапный метод с распределением работ в пределах допусков на заданную периодичность данной формы предполагает разделение всего необходимого объема работ на несколько этапов, которые выполняются в промежутках между рейсами летательного аппарата (ЛА). Такой метод приемлем только для нетрудоемких форм ТО (рис. 3).

Прямоугольниками на рисунке показаны условные трудоемкости работ. Работы, которые следует выполнить при налете τф, разбиваются на несколько частей, которые необходимо выполнить в пределах допуска ±Δτф на периодичность данной формы ТО.

·       Поэтапный метод с распределенной трудоемкостью состоит в том, что выполнение отдельных объектов работ более трудоемких периодических форм совмещается с обслуживанием менее трудоемких (рис. 4а).

В данном случае каждое периодическое ТО включает объем работ первой по трудоемкости формы регламента ТФ1 и трудоемкости дополнительных работ ΔТфi, присущих каждой последующей форме регламента. Так, для регламентов с обслуживанием ЛА по формам Ф1, Ф2 и Ф3 будем иметь ТФ2=Тф1+ΔТф2; ТФ3=Тф1+ΔТф2+ΔТф3=Тф2+ +ΔТф3, где ТФ1, ТФ2, ТФ3 – трудоемкость периодического ТО по формам Ф1, Ф2, Ф3 соответственно; ΔТФ2, ΔТФ3 – трудоемкость дополнительных работ при обслуживании по Ф2 и Ф3 соответственно.

При таком методе организации ТО трудоемкость каждого этапа примерно одинаковая (рис. 4б), что позволяет сократить продолжительность ТО при более трудоемких формах, создать условия для равномерной загрузки цеха периодического ТО и повысить эффективность использования ЛА. Однако данный метод не обеспечивает необходимую степень увеличения налета [1].

Анализ существующих методов планирования ТОиР представлен в [2–4].

Решаемая задача ТО представляет собой совокупность процедур , выполняемых на объекте для поддержания его технической исправности. Общее число процедур ТО на временном интервале T=[t1, tn], задаваемом начальной и конечной точками (t1 и tn соответственно), формирует множество процедур P (рис. 5).

Имеется множество работ W={wk}, которые могут быть выполнены при ТО.

Процедура ТО представляет собой множество работ: W={wk}, где wk – k-я работа; Wn – множество работ, входящих в состав процедуры ТО pn.

Задача алгоритма планирования ТО состоит в формировании множества T и определении множеств Wi, , для проведения работ в процедуре ТО. При формировании множества ТО и множества входящих в него работ следует учитывать ограничения, накладываемые различными источниками.

Существует m единиц оборудования, для которого требуется провести работы по поддержанию исправности и работоспособности. Существует множество работ wk–Wn, k=[1, kmax], ТО и планового ремонта специального оборудования, выполняемых в ходе процедур ТО.

Постановка задачи: определить состав и время проведения процедур ТО, при которых выбранный критерий будет принимать экстремальное (минимальное) значение, то есть определить все xkn, при которых  S®min, T=max(Tn)®min, где xkn – логическая переменная, значение которой определяется входимостью k-й работы в n-ю процедуру ТО: если k-я работа входит в n-ю процедуру, то xkn=1, иначе xkn=0:

S – общие материально-технические затраты на производство ТО: , где sk – материально-технические затраты на k-ю работу, k=[1, kmax], где kmax – общее количество работ в системе; Tn – трудоемкость n-й процедуры ТО: , где rk – трудоемкость k-й работы, k=[1, kmax], где kmax – общее количество работ в системе.

Поставленная задача должна быть решена с учетом специальных ограничений.

Для реализации поставленной цели сведем задачу к общей задаче проектирования конфигурации (configuration design) или синтеза конфигурации, где под конфигурацией понимается распределение конкретных работ по процедурам [2].

Выделяются два типа задач построения конфигурации систем – отбор и/или размещение, построение иерархии системы. Решаемая задача относится к первому типу, на ее входе множество элементов/компонентов, которое разделено на подмножества.

Задача синтеза конфигурации относится к группе задач структурного синтеза с наложенными ограничениями. В общем виде задача структурного синтеза заключается в определении некоторого варианта структуры объекта или системы. Под комбинаторной понимается такая задача, решение которой сводится к выбору варианта из конечного множества решений.

Задача структурного синтеза проектных решений с точки зрения возможности формализации относится к наиболее сложным. Это связано с тем, что, с одной стороны, свойства синтезируемого объекта зависят от большого числа зачастую случайных, противоречивых, но не до конца исследованных факторов. Эта причина имеет объективный характер. С другой стороны, при решении задачи синтеза часто приходится выбирать вариант из множества очень большой конечной или даже счетной мощности. Кроме того, если задача синтеза поставлена в терминах некоторой формальной системы, для реализации такого выбора необходимо решить задачу очень высокой размерности. Например, решить задачу дискретной оптимизации на множестве, состоящем из большого числа элементов. При этом могут потребоваться вычислительные мощности, превосходящие возможности современных компьютеров.

Большая размерность задач синтеза технических объектов делает целесообразным применение блочно-иерархического подхода, при котором весь процесс синтеза объекта разбивается на совокупность взаимосвязанных иерархических уровней [5]. Это значит, что синтезируется не весь объект в целом – на каждом иерархическом уровне син- тезируются определенные подсистемы, уровень детализации которых соответствует принятому способу декомпозиции системы на подсистемы. Такой подход существенно упрощает решение задачи синтеза.

Для решения подобных задач применимы многие современные методы поиска решений с некоторыми модификациями. В ходе решения задачи происходит манипулирование не обычными числовыми значениями, а разнородными объектами (процедурами), выбираемыми из соответствующих множеств. Причем свойства экземпляров объектов не являются плавно меняющимися от экземпляра к экземпляру, а подвержены непредсказуемым изменениям по причине разнородности типов свойств и различной природы значений свойств.

Среди всех подходов к решению задачи структурного синтеза наибольшее распространение в системах автоматизированного проектирования получили различные методы, принадлежащие к классу комбинаторно-логических. В основе этого подхода лежит хорошо организованный перебор в массиве решений, являющихся аналогами и прототипами.

Рассмотрим основные допущения:

–      проектируемый объект (будь то техническая система или процесс) имеет структуру;

–      проектируемый объект принадлежит к некоторому классу объектов (множество аналогов и прототипов), имеющих одинаковое функциональное назначение;

–      множество аналогов и прототипов обладает достаточной мощностью для того, чтобы поиск новых сочетаний в этом комбинаторном пространстве был результативным;

–      составные части объектов класса обладают хорошими комбинаторными способностями.

Это значит, что принципы действия объектов не различаются настолько, чтобы запретить объединение разных компонент в составе нового объекта.

Большинство комбинаторных задач относится к классу NP-трудных, а значит, требует особого внимания и специфических методов решения. Если в комбинаторной задаче присутствует набор ограничений на переменные, значения которых необходимо проанализировать, целесообразно применение методов решения задач с ограничениями. Класс таких задач называется Constraint Satisfaction Problem (CSP). Для решения подобных задач разработаны соответствующие методы и инструментальные средства. В настоящее время данная область активно исследуется, появляются все новые подходы, обнаруживаются их недостатки и достоинства (см., например, [6–9]).

Метод удовлетворения (распространения) ограничений (CSP) является одним из подходов искусственного интеллекта, применяемых для решения различных сложных и нестандартных задач, в том числе подобных комбинаторным. Программирование в ограничениях требует только описания задачи, но не заставляет разработчика определять алгоритм ее решения.

Говоря неформально, задача удовлетворения ограничений – это задача, состоящая из конечного числа переменных, каждая из которых связана с некоторой областью ее определения (дискретной или непрерывной), и конечного множества ограничений на множества значений переменных, принимаемых одновременно. Решение задачи удовлетворения ограничений состоит в присваивании значения каждой переменной так, чтобы одновременно удовлетворялись все ограничения. Целью может являться нахождение как одного такого набора (любого или с заданным свойством), так и всех наборов.

Представление же проблемы в виде задачи распространения ограничений позволяет применять для ее решения наряду со специальными методами прикладной области достаточно эффективные и универсальные методы решения задач распространения ограничений. В настоящее время техника распространения ограничений все чаще используется как основа для решения различных прикладных задач, таких как временные рассуждения, задачи ресурсного и календарного планирования, математическое и инженерное моделирование, задачи на графах и т.д.

Задача и модель представляются в этом случае как совокупность отношений, которые соответствуют связям, существующим между переменными задачи. Эти отношения, называемые общим термином ограничения, могут иметь вид уравнений, неравенств, логических выражений и т.п.

Система работ представляет собой набор данных, на основе которых формируется состав работ в каждом ТО. Она должна содержать информацию о функциональной декомпозиции ра- бот в виде иерархической структуры компонентов, образующих состав работ; формальное описание закономерностей, определяющих возможность включения данной работы в состав текущего ТО; механизм, позволяющий проверять получен- ное множество Wn работ на соответствие требованиям.

Построение системы работ является основой для дальнейшего многократного формирования множества графиков ТО [2].

Для описания функциональной декомпозиции работ в виде иерархической структуры компонентов, образующих состав работ, представим онтологию предметной области.

Она включает несколько областей: справочник изделий, к которым применяется ТО; справочник работ, из которых формируются процедуры, формирующие ТО; взаимосвязь всех компонентов с учетом принадлежностей, свойств и ограничений.

Объекты предметной области: <Изделие, ТО, Процедура, Работа>.

Множество процедур: ПР <ПР1, ПР2, …, ПРn>.

Множество работ: РБ <РБ1, РБ2, …, РБk>.

Изделие: И <И1>.

Оборудование: ОБ <ОБ1, ОБ2, …, ОБg>.

Техническое обслуживание: ТО.

Объекты и их свойства:

Объект ТО имеет следующие свойства: ТО.Трудоемкость, ТО.Затраты, ТО.Время_выпол­нения;

Объект ПР имеет следующие свойства: ПР.Трудоемкость, ПР.Затраты, ПР.Время_выпол­нения, ПР.Тип;

Объект РБ имеет следующие свойства: РБ.Тру­доемкость, РБ.Затраты, РБ.Время_выполнения, РБ.Тип, РБ.Совместная_выполнимость;

Объект И имеет следующие свойства: И.Кол-во_отказов, И.Время_наработки_на_отказ, И.Вре­мя_наработки, И.Тип, И.Время_простоя;

Объект ОБ имеет следующие свойства: ОБ. Время_наработки, ОБ.Кол-во_отказов, ОБ.Вре­мя_простоя, ОБ.Время_наработки_на_отказ.

Перечень требований ТР: {ТР}.Затраты_доп, {ТР}.Трудоемкость_доп, {ТР}.Надежность, {ТР}. Время_простоя_макс, {ТР}.Затраты_пр_мин, {ТР}.Затраты_пр_макс, {ТР}.Трудоемкость_пр_ мин, {ТР}.Трудоемкость_пр_макс, {ТР}.Время_ наработки_макс, {ТР}.Время_наработки_мин, {ТР}.Время_простоя_макс, {ТР}.Время_простоя_ мин, {ТР}.Время_выполнения_макс, {ТР}.Время_ выполнения_мин, {ТР}.Время_макс_м_раб.

Ограничения содержатся в функциональной конфигурации и являются основой онтологии предметной области задачи. Ограничения имеют форму логических или функциональных выражений, а также таблиц значений. Функциональные выражения могут быть использованы решателем для вычисления любого аргумента при остальных известных. Если какие-либо из аргументов заданы в виде значения сложной формы (диапазоны, списки значений и т.д.), искомое значение параметра также будет сложной формы.

К параметрам, определенным в проектной конфигурации, применяются выражения ограничений, описанных в функциональной конфигурации, и требования к значениям параметров.

Ограничения делятся на два вида:

–      функции, позволяющие вычислить агрегативные свойства (то есть свойства более крупного компонента, вычисляемые из соответствующих свойств входящих в него компонентов, например масса компонента);

–      ограничения (неравенства) проверки соответствия созданной конфигурации заданным требованиям; данные аксиомы могут храниться в объектах крупных законченных компонентов (узлов) либо в объекте изделия.

Каждое такое ограничение может быть реализовано в виде n-сторонней функциональной зависимости, то есть в виде одной и той же зависимости, но выраженной через разные аргументы.

Описание закономерностей, определяющих возможность включения данной работы в состав текущего ТО, указываются в виде ограничений.

При решении задачи были использованы следующие ограничения:

–      период времени между работами (Δt) должен быть меньше максимально допустимого промежутка времени между работами (Δtmax) либо равен ему;

–      если работы, определенные матрицей совместимости, выполняются в одной процедуре ТО, их стоимость снижается на 20 %.

Алгоритм и предлагаемая методика

На основе обзора существующих методов [2] была сформулирована методика поиска, основанная на комбинации метода перебора с методами предварительного ограничения пространства поиска.

В отличие от метода полного перебора данная методика предполагает предварительные этапы ограничения пространства поиска, чем обеспечивается значительное сокращение времени поиска решения.

Методика состоит из трех этапов.

На первом этапе происходит обеспечение совместимости в узлах путем проверки унарных требований к параметрам отдельных компонентов с использованием алгоритма NC-1. На этом этапе удовлетворяются ограничения, связанные с уже известными параметрами компонентов (требования к параметрам компонентов).

Алгоритм обеспечения совместимости в узлах NC-1 позволяет удалить из областей определения всех переменных задачи значения, которые не удовлетворяют унарным ограничениям [9, 10].

Достижение совместности в узлах сводится к просмотру каждого элемента в каждой области и проверке того, удовлетворяет ли это значение унарным ограничениям на эту переменную. Все значения, нарушающие унарные ограничения, удаляются из этих областей.

После завершения алгоритма исходная задача будет сведена к задаче, которая является совместной в узлах.

На втором этапе производится предварительная проверка компонентов методом Forward Checking (метод предварительной проверки). На этом этапе происходит попарное сравнение компонентов справочников с целью удаления компонентов, не совместимых между собой.

С помощью метода предварительной проверки Forward Checking пространство поиска может быть значительно уменьшено или полностью разрешено [11, 12].

Основную идею метода можно выразить следующим образом: если при назначении какой-либо переменной значения ее домена набор неравенств становится несовместным, следует удалить несовместные значения из доменов остальных переменных и продолжить поиск, а если текущий домен пуст, то происходит откат на предыдущий уровень [13]. Домен – набор компонентов (работ) из справочника.

Следует начинать поиск с переменных, у которых наименьшие по количеству значений домены.

Адаптированный под данную задачу алгоритм выглядит следующим образом:

1.        Переменные сортируются в порядке возрастания количества значений в домене

2.        Для каждой переменной xi:

a.      Переменной xi ставится в соответствие каждое значение из ее домена

                    i.      Для каждой переменной yi:

1.        Переменной yi ставится в соответствие каждое значение из ее домена

a.        Проверяется выполнение бинарного ограничения на совместимость значений параметра (компонентов) xi и yi

b.        Если не выполняется, то удаляется текущее значение xi из соответствующего домена

На третьем этапе производится поиск решений с использованием метода Back Tracking. Для этого происходит обход дерева, производятся вычисление неизвестных значений параметров компонентов и проверка соответствия расчетных параметров требованиям.

Поиск с возвратом (Backtracking). Алгоритм поиска с возвратом для решения задач удовлетворения ограничений CSP составлен по принципу рекурсивного поиска в глубину [9, 14].

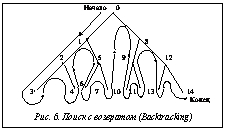
Данный метод предполагает перебор всех возможных комбинаций путем обхода дерева вариантов компоновки с возвратами при невыполнении ограничений (рис. 6).

Метод позволяет произвести полный обход всех комбинаций компонентов и найти все возможные решения.

Алгоритм:

–      поиск всех дополнительных вариантов распределения работ по процедурам ТО, по которым выполняются все ограничения;

–      упорядочение полученных решений по целевой функции;

–      поиск решения в соответствии с наилучшими значениями целевой функции.

Тестирование и анализ результатов применения методики

Предлагаемая методика и алгоритмы были проверены на простом примере формирования процедур ТО самолета Ту-214. Процесс основан на формировании процедур путем перебора вариантов с предварительным ограничением пространства поиска. Методика состоит из трех этапов, применяющих к задаче последовательно три разных метода.

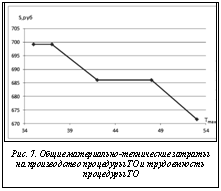
При сравнении общих материально-техничес­ких затрат на производство ТО и трудоемкости процедуры ТО до и после применения метода наблюдается значительное падение. Данный метод позволяет снизить затраты на ТО на 8,5 % и максимальное время выполнения процедуры на 34 % (см. рис. 7).

Таким образом, тестирование показало применимость методики для решения задач структурного синтеза. Предложенная методика позволяет значительно сократить пространство поиска решений.

Реализация алгоритма предполагает наличие раздельных модулей: парсера (решателя) ограничений и генерации и поиска решений. Это позволяет без перепрограммирования производить настройку на конкретные условия, что значительно упрощает поддержку системы в целом и расширяет области ее использования.

В дальнейших планах – реализация данной методики в виде обобщенного решателя и алгоритмов формирования множества допустимых комбинаций в онтологических структурах. При разработке решателя необходимо исследовать и разработать язык и средства создания и использования ограничений, а также апробировать алгоритмы на более объемном примере и разработать модели и интерфейсы интеграции в существующие PDM- и ЕАМ-системы.

Литература

1.     Чинючин Ю.М., Полякова И.Ф. Основы технической эксплуатации и ремонта авиационной техники. М.: МГТУГА. 2004. Ч. 1. 81 с.

2.     Федотова А.В., Овсянников М.В., Таратухин В.В. Применение метода программирования в ограничениях при решении задач планирования технического обслуживания и ремонта воздушных судов // Бизнес-информатика. 2013. № 1 (23). С. 28–36.

3.     Федотова А.В., Овсянников М.В. Исследование методов планирования периодических процессов обслуживания (на примере ТОРО) // Реинжиниринг бизнес-процессов на основе современных информационных технологий. Системы управления знаниями (РБП-СУЗ-2012): тр. XV науч.-практич. конф. М.: МЭСИ. 2012. C. 238–245.

4.     Куприянов Ю.В., Овсянников М.В., Таратухин В.В., Федотова А.В. Исследование методов планирования периодических процессов обслуживания // IS&IT’12: тр. Конгресса по интеллект. системам и информ. технологиям. М.: Физматлит, 2012. Т. 2. C. 287–294.

5.     Wielinga B., Schreiber G. Configuration Design Problem Solving. IEEE Intelligent Systems, 1997, vol. 12, pp. 49–56.

6.     Рассел С., Норвиг П. Искусственный интеллект: современный подход. Киев: Вильямс, 2006. 1408 с.

7.     Apt K.R. Principles of Constraint Programming, Cam­bridge Univ. Press, 2003.

8.     Van Beek P., Walsh T. Principles of Constraint Program­ming and Constraint Processing: A Review, AI Magazine, 2004, vol. 25, no. 4. pp. 105–106.

9.     Семенов А.Л. Методы распространения ограничений: основные концепции // PSI’03/ИМРО – Интервальная математика и методы распространения ограничений: тр. 5-й Междунар. конф. Новосибирск, 2003. С. 19–31.

10.  Benhamou F., Older W. Applying Interval Arithmetic to Real, Integer and Boolean Constraints. Journ. of Logic Program­ming 32, 1997, pp. 1–24.

11.  Gent Ian. Artificial Intelligence: Constraint Programming. URL: http://www.dcs.st-and.ac.uk/~ipg/AI/ (дата обращения: 11.09.2013).

12.  Bartak R. On-line guide to Constraint Programming. URL: http://ktilinux.ms.mff.cuni.cz/~bartak/constraints/ (дата обращения: 11.09.2013).

13.  Беляев С.А. Проблема разрешения constraint при решении задач комбинаторной оптимизации. URL: http://constr. chat.ru/ARTICLES/cresprob_20010608.htm (дата обращения: 11.09.2013).

14.  Dechter R., Frost D. Backjump-based backtracking for constraint satisfaction problems. Artificial Intelligence, 2002, no. 136 (2), pp. 147–188.

15.  Буханов С.А., Овсянников М.В. Управление конфигурацией с использование метода программирования в ограничениях // Эффективные методы автоматизации подготовки и планирования производства: сб. науч. тр. М.: Спектр, 2011. С. 150–156.

16.  Буханов С.А., Овсянников М.В. Управление конфигурацией на основе онтологии предметной области // AIS-IT’10: тр. Конгресса по интеллект. системам и информ. технологиям. М.: Физматлит, 2010. Т. 1. С. 399–403.

References

1. Chinyuchin Yu.M., Polyakova I.F. Osnovy tekhnicheskoy ekspluatatsii i remonta aviatsionnoy tekhniki [Basics of technical exploitation and repair of aircraft equipment]. Moscow, Moscow St. Tech. Univ. of Civil Aviation Publ., 2004, part 1, 81 p.

2. Fedotova A.V., Ovsyannikov M.V., Taratukhin V.V. Application of constraints satisfaction method when solving problems of planning maintenance and repair of aircraft equipment. Biznesinformatika [Business Informatics]. 2013, no. 1 (23), pp. 28–36.

3. Fedotova A.V., Ovsyannikov M.V. Research in planning periodic processes maintenance methods (TORO as an ex.). Trudy XV nauchno-prakt. konf. “Reinzhiniring biznes-protsessov na osnove sovremennykh informatsionnykh tekhnologiy. Sistemy upravleniya znaniyami (RBP-SUZ-2012)” [Proc. 15th sci. and pract. conf. “Reengineering business processes based on modern IT. Systems of knowledge management (RBP-SUZ-2012)”]. Moscow, Moscow St. Univ. of Economics, Statistics and Informatics (MESI) Publ., 2012, pp. 238–245.

4. Kupriyanov Yu.V., Ovsyannikov M.V., Taratukhin V.V., Fedotova A.V. Researching planning methods of periodic maintenance processes. Trudy Kongressa po intellektualnym sistemam i informatsionnym tekhnologiyam “IS&IT’12” [Proc. congress on intelligent systems and IT “IS&IT’12”]. Moscow, Fizmatlit Publ., 2012, vol. 2, pp. 287–294.

5. Wielinga B., Schreiber G. Configuration Design Problem Solving. IEEE Intelligent Systems. 1997, vol. 12, pp. 49–56.

6. Rassel S., Norvig P. Artificial Intelligence: A Modern Approach. Prentice Hall Publ., 2009, 3 ed., 1152 p.

7. Apt K.R. Principles of Constraint Programming. Cambridge University Press, 2003.

8. Van Beek P., Walsh T. Principles of Constraint Programming and Constraint Processing: A review. AI Magazine. 2004, vol. 25, no. 4, pp. 105–106.

9. Semenov A.L. Methods for constraint distributing: basic consepts. PSI’03/IMRO – Intervalnaya matematika i metody rasprostraneniya ogranicheniy: tr. 5 Mezhdunar. konf. [Proc. 5th int. conf.: PSI’03/IMRO – Interval mathematics and methods for constraint distributing]. 2003, pp. 19–31.

10. Benhamou F., Older W. Applying Interval Arithmetic to Real, Integer and Boolean Constraints. Journ. of Logic Programming. 1997, vol. 32, pp. 1–24.

11. Gent Ian. Artificial Intelligence: constraint programming. Available at: http://www.dcs.st-and.ac.uk/~ipg/AI/ (accessed 11 September 2013).

12. Bartak R. On-line guide to constraint programming. Available at: http://ktilinux.ms.mff.cuni.cz/~bartak/constraints/ (accessed 11 September 2013).

13. Belyaev S.A. Problema razresheniya constraint pri reshenii zadach kombinatornoy optimizatsii [The problem of constraint resolution when solving combinatorial optimization tascs]. Available at: http://constr.chat.ru/ARTICLES/cresprob_20010608.htm (accessed 11 September 2013).

14. Dechter R., Frost D. Backjump-based backtracking for constraint satisfaction problems. Artificial Intelligence. 2002, no. 136 (2), pp. 147–188.

15. Bukhanov S.A., Ovsyannikov M.V. Configuration control using constraint programming. Effektivnye metody avtomatizatsii podgotovki i planirovaniya proizvodstva: sb. nauch. tr. [Efficient methods of automated production preparing and planning: proc.]. Мoscow, Spektr Publ., 2011, pp. 150–156.

16. Bukhanov S.A., Ovsyannikov M.V. Configuration control based on object domain ontology. AIS-IT’10: tr. Kongressa po intellekt. sistemam i inform. tekhnologiyam [Proc. congress on intelligent systems and IT “AIS-IT’10”]. Moscow, Fizmatlit Publ., 2010, vol. 1, pp. 399–403.