Программные продукты и системы

Сложность описания многозвенного робота-манипулятора как объекта управления (ОУ) и неопределенность среды функционирования ставят задачу разработки интеллектуальной системы управления (ИСУ), способной функционировать в условиях неполной информации о среде функционирования, возмущениях и информационного риска [1].

Построение ИСУ роботом-манипулятором возможно с применением технологий мягких вычислений [2−5]. Проектирование ИСУ роботом-манипулятором с тремя степенями свободы с единой БЗ, а также метод декомпозиции управления рассмотрены в [6]. Продемонстрировано, что использование единой БЗ приводит к усложнению и увеличению времени создания БЗ, повышению требований к вычислительным ресурсам процессора, на котором создаются БЗ, и объему памяти системы, в которой размещается БЗ. Декомпозиция управления – разделение единой БЗ на несколько независимых – значительно упрощает процесс проектирования ИСУ и снижает требования к вычислительным ресурсам. Однако в результате рассогласования работы разделенных независимых БЗ несколько снижается качество управления.

В данной статье для устранения отмеченного недостатка предлагается метод организации координационного управления с применением технологий квантовых вычислений.

  Технологии квантовых вычислений в самоорганизующихся ИСУ

Технологии квантовых вычислений для создания самоорганизующихся БЗ интеллектуальных регуляторов рассмотрены в [7]. Описан новый вид квантового поискового алгоритма на обобщенном пространстве БЗ нечетких регуляторов (НР), спроектированных на основе технологий мягких вычислений, – квантовый нечеткий вывод (КНВ) для проектирования обобщенного робастного сигнала управления. Модель КНВ реализует самоорганизацию БЗ, основывается на физических законах теории квантовых вычислений [8−11] и использовании четырех операторов: суперпозиции, квантовой корреляции, интерференции и измерения. Первые три являются унитарными, обратимыми квантовыми операторами, а четвертый (оператор измерения) – классическим (необратимым).

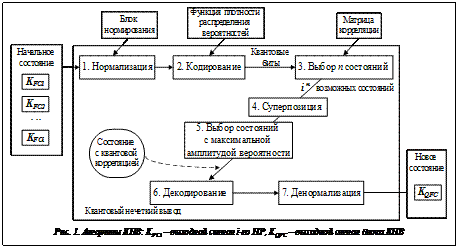На рисунке 1 представлен алгоритм КНВ.

Алгоритм КНВ [9] включает следующую последовательность шагов.

1.     Нормализация. Приведение входных сигналов к нормализованным состояниям.

2.     Кодирование. Построение всех нормализованных состояний  и  для текущих входных переменных и вычисление амплитуд вероятностей  и  из соответствующих гистограмм.

3.     Выбор типа квантовой корреляции для построения выходных сигналов управления. В рамках данной работы рассматриваются три типа смешанных корреляций [12, 13]: пространственная, пространственно-временная и временная [14]. Зависимость выходных сигналов определяется корреляцией наборов входных коэффициентов, где каждый набор является запутанным состоянием [15].

4.     Построение суперпозиции запутанных состояний.

5.     Измерение интеллектуального квантового состояния. Выбор состояния с максимальной амплитудой вероятности [16, 17].

6.     Декодирование. Вычисление выходного значения соответствующего сигнала.

7.     Денормализация. Вычисление денормализованного выходного значения.

Создание КНВ производится с помощью интеллектуального инструментария оптимизатор БЗ (ОБЗ) на основе квантовых вычислений (разработка подтверждена свид. о гос. регистр. прогр. для ЭВМ № 2011616869 от 5.09.2011 г., авторы: С.В. Ульянов, Л.В. Литвинцева, А.А. Мишин, С.В. Сорокин).

Рассмотрим метод включения алгоритма КНВ в ИСУ роботом-манипулятором на основе ОБЗ на мягких вычислениях с разделенным управлением.

  Организация координационного управления роботом-манипулятором

В выбранной конфигурации структуры ИСУ реализованы три НР, каждый из которых независимо от других управляет одним из трех звеньев.

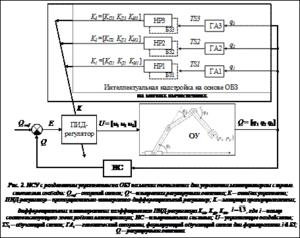
На рисунке 2 приведена структурная схема ИСУ манипулятором с тремя степенями свободы на основе ОБЗ на мягких вычислениях с разделенным управлением.

Штатной ситуацией управления для i-го НР является типовая ситуация управления, в условиях которой получен обучающий сигнал TSi.

Непредвиденные ситуации управления разделяются на внешние и внутренние. К внешним относятся возмущающие воздействия, например, принудительное изменение положения ОУ в начале или в процессе работы, изменение опорных сигналов и др., к внутренним – изменения параметров компонентов системы управления (ограничения, шумы и задержки сигналов).

Рассмотрим работу в условиях внешних непредвиденных ситуаций.

Спроектированная ИСУ на ОБЗ на мягких вычислениях с разделенным управлением, представленная на рисунке 2, может содержать информацию о трех ситуациях управления (штатных или непредвиденных) для каждого из трех звеньев.

Рассмотрим пример, когда в спроектированной ИСУ на ОБЗ на мягких вычислениях с разделенным управлением НР1 содержит информацию о штатной ситуации 1 для звена 1 (БЗ1), НР2 – для звена 2 (БЗ2) и НР3 – для звена 3 (БЗ3).

Блок КНВ, включенный в модель ИСУ на ОБЗ на мягких вычислениях, реализует самоорганизацию БЗ НР. В этом случае имеется возможность не только объединять информацию о штатной ситуации 1 для трех звеньев, но и извлекать дополнительную информацию (методами квантовых вычислений и квантовой теории информации) из реакции спроектированных БЗ для реализации робастного управления в штатных и непредвиденных ситуациях управления (которые не включены в существующие спроектированные БЗ).

При этом сами БЗ, реакции которых используются для проектирования робастного управления, в нештатных ситуациях могут быть неробастными.

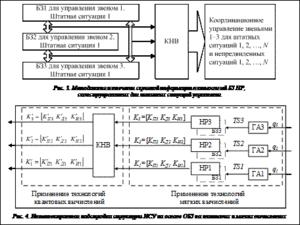
Схема извлечения скрытой информации о взаимосвязях существующих НР (спроектированных с использованием технологий мягких вычислений) для трех звеньев манипулятора с БЗ, полученных для штатных ситуаций управления с использованием блока КНВ, приведена на рисунке 3.

Схема подключения блока КНВ в интеллектуальную надстройку системы управления показана на рисунке 4, на котором выделены блоки, спроектированные с использованием технологий мягких и квантовых вычислений.

Далее ИСУ с использованием КНВ будем называть ИСУ на основе ОБЗ на квантовых вычислениях.

  Качество ИСУ роботом-манипулятором с квантовым нечетким выводом

Для исследования качества систем управления были разработаны модель в среде MatLab/Simulink и физический макет робота-манипулятора с тремя степенями свободы.

Для оценки работы систем управления (как для MatLab/Simulink-моделей, так и для физического макета) введена система критериев качества, учитывающая методы оценки переходных процессов теории автоматического управления. Данные методы адаптированы для рассматриваемого ОУ следующим образом.

1.     Решение задачи позиционирования в штатных ситуациях управления PTSKCS (Position Task Solution in known control situations), соответствующий весовой коэффициент w1=0,1.

2.     Решение задачи позиционирования в непредвиденных ситуациях управления PTSACCS (Position Task Solution in the above considered control situations), w2=0,4.

3.     Быстродействие IT, w3=0,2.

4.     Относительное значение перерегулирования s, w4=0,5.

5.     Относительная ошибка позиционирования звеньев e, w5=0,1.

6.     Время одной итерации t, w6=0,1.

7.     Сложность реализации управления P, w7=0,05.

8.     Общая оценка управления FCB (Full Control Behavior); определяется как FCB=w1×P[PTSKCS]+ +w2×P[PTSACCS]+w3×P[IT]+w4×P[s]+w5×P[e]+w6×P[t]+ +w7×P.

Методика проведения экспериментов и описание критериев качества приведены в [14].

Оценка работы рассмотренных ИСУ производится по результатам MatLab/Simulink-моделиро­вания и серии экспериментов на физическом ОУ.

Сравним работу ИяСУ на ОБЗ на квантовых вычислениях с применением пространственной, пространственно-временной и временной корреляций и ИСУ на ОБЗ на основе мягких вычислений с разделенным управлением.

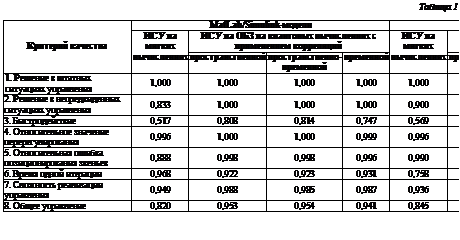
В таблице 1 приведено сравнение ИСУ соответственно для MatLab/Simulink-моделей и физического макета робота-манипулятора по введенному ряду критериев качества.

Из результатов сравнения видно, что при включении в структуру ИСУ с разделенным управлением блока КНВ задача управления решается как для штатных, так и для непредвиденных ситуаций управления, увеличивается быстродействие, улучшается показатель точности позиционирования, уменьшается показатель сложности реализации управления.

При использовании ИСУ на ОБЗ на квантовых вычислениях в отличие от ИСУ на ОБЗ на мягких вычислениях с разделенным управлением все показатели качества улучшаются в результате устранения рассогласованности в работе разделенных независимых БЗ путем организации координационного управления. Причем, если для MatLab/Si­mulink-моделей наилучший показатель общего качества управления обеспечивается при использовании ИСУ на ОБЗ на квантовых вычислениях с применением пространственно-временной корреляции, то физическое тестирование определяет оптимальным выбор пространственной корреляции.

Рассмотрим ИСУ на ОБЗ на квантовых вычислениях только с применением пространственной корреляции.

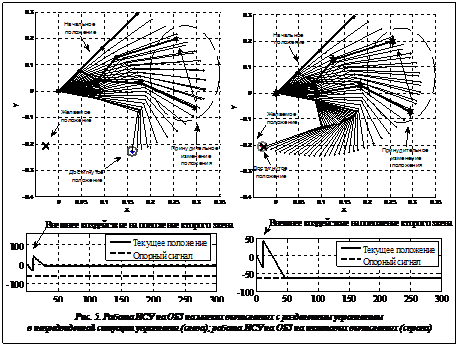Продемонстрируем работу ИСУ на ОБЗ на мягких вычислениях с разделенным управлением в условиях непредвиденной ситуации управления (рис. 5) по сравнению с ИСУ на ОБЗ на квантовых вычислениях. В качестве непредвиденной выступает ситуация с принудительным перемещением второго звена.

Из рисунка 5 видно, что в рассмотренной непредвиденной ситуации управления ИСУ на ОБЗ на квантовых вычислениях справляется с задачей позиционирования с заданной точностью в отличие от ИСУ на ОБЗ на мягких вычислениях с разделенным управлением.

Неспособность ИСУ на ОБЗ на мягких вычислениях решить задачу точного позиционного управления также иллюстрируется на рисунке 5: НР, отвечающий за управление вторым звеном, за отведенное на работу время так и не смог реабилитироваться после мощного внешнего воздействия, в результате чего ошибка позиционирования второго звена составила более 50 градусов, цель управления не достигнута и система управления в целом оказалась неробастной.

Ранее рассмотренные непредвиденные ситуации относились к внешним возмущающим воздействиям. Введем ряд внутренних непредвиденных ситуаций (изменения ограничений канала управления), разделим второй критерий качества – решение задачи позиционирования в непредвиденных ситуациях управления – на две составляющие.

Критерий 2.1. Решение задачи позиционирования в непредвиденных ситуациях управления: внешние возмущающие воздействия PTSACCS1, w21=0,2.

Критерий 2.2. Решение задачи позиционирования в непредвиденных ситуациях управления: изменения внутренних параметров PTSACCS2, w22=0,2.

Тогда критерий 8 – общая оценка управления – будет определяться следующим образом: FCB= = w1×P[PTSKCS] + w21×P[PTSACCS1] + w22×P[PTSACCS2]+ +w3×P[IT]+w4×P[s]+w5×P[e]+w6×P[t]+w7×P, сумма весовых коэффициентов по-прежнему будет равна единице.

Сравним ИСУ на ОБЗ на мягких вычислениях с одним НР и ИСУ на ОБЗ на квантовых вычислениях.

В таблице 2 приведено сравнение ИСУ соответственно для MatLab/Simulink-моделей и физического макета робота-манипулятора по обновленному ряду критериев качества.

Из результатов сравнения видно, что и ИСУ на ОБЗ на мягких вычислениях с одним НР, и ИСУ на ОБЗ на квантовых вычислениях решают задачу позиционирования для штатных и внешних непредвиденных ситуаций, однако ИСУ на ОБЗ на мягких вычислениях с одним НР в отличие от ИСУ на ОБЗ на квантовых вычислениях не всегда справляется с внутренними непредвиденными ситуациями, вследствие чего общая оценка для ИСУ на ОБЗ на квантовых вычислениях выше как для MatLab/Simulink-моделей, так и для физического макета робота-манипулятора.

Продемонстрируем работу ИСУ на ОБЗ на мягких вычислениях с одним НР в условиях внутренней непредвиденной ситуации управления (рис. 6) по сравнению с ИСУ на ОБЗ на квантовых вычислениях. В качестве непредвиденной ситуации выступает вариант с изменением в процессе работы ограничений в канале управления.

Из рисунка 6 видно, что ИСУ на ОБЗ на квантовых вычислениях обеспечивает лучшее качество решения, чем ИСУ на ОБЗ на мягких вычислениях с одним НР.

Рассмотрим законы управления, формируемые рассмотренными типами ИСУ на основе мягких и квантовых вычислений.

На рисунке 7 закон управления, формируемый ИСУ на ОБЗ на квантовых вычислениях, обозначен как QFC, формируемый ИСУ на ОБЗ на мягких вычислениях с одним НР – FC, формируемый ИСУ на ОБЗ на мягких вычислениях с разделенным управлением – FC Decomposition.

Из рисунка 7 (слева) видно, что законы управления, формируемые ИСУ на ОБЗ на квантовых вычислениях в условиях внешних возмущающих воздействий, аналогичны формируемым ИСУ на ОБЗ на мягких вычислениях с одним НР, однако амплитуда закона управления в момент внешнего воздействия значительно ниже для ИСУ на ОБЗ на квантовых вычислениях. Законы управления, сформированные ИСУ на ОБЗ на мягких вычислениях с разделенным управлением, приобрели колебательный характер.

Более того, из правой части рисунка видно, что в ситуации внешних возмущающих воздействий закон управления, формируемый ИСУ на ОБЗ на мягких вычислениях с одним НР для второго звена, имеет участок локальной неустойчивости, в то время как ИСУ на ОБЗ на квантовых вычислениях формирует законы робастного управления.

Таким образом, минимальный расход полезного ресурса при формировании законов управления обеспечивается при использовании ИСУ на ОБЗ на квантовых вычислениях.

В результате сравнения работы рассмотренных типов систем управления можно сделать следующие выводы.

·       Общая оценка качества управления выше в случае применения ИСУ на ОБЗ на квантовых вычислениях (для всех рассмотренных типов корреляций) по сравнению с ИСУ на ОБЗ на мягких вычислениях с разделенным управлением, что обусловлено введением в структуру ИСУ дополнительного звена КНВ, организующего координационное управление. Причем, если в результате тестирования MatLab/Simulink-моделей лучшими показателями обладала ИСУ, использующая пространственно-временную корреляцию, то физическое тестирование определило использование пространственной корреляции как наиболее оптимальное.

·       Общая оценка качества управления улучшается при использовании ИСУ на ОБЗ на квантовых вычислениях по сравнению с использованием ИСУ на ОБЗ на мягких вычислениях с одним НР. ИСУ на ОБЗ на мягких вычислениях с одним НР способна решать задачу позиционирования в условиях внешних непредвиденных ситуаций, однако не всегда справляется с внутренними непредвиденными ситуациями.

Данный результат примечателен тем, что при организации координационного управления за счет единой БЗ (соответственно при использовании одного НР в ИСУ на ОБЗ на мягких вычислениях) количество входных переменных, то есть параметров, определяющих функционирование системы, ограничено вычислительными ресурсами процессора, на котором создается БЗ, и объемом памяти системы, в которой размещается БЗ.

Возможность декомпозиции управления (разделения одной БЗ на несколько однотипных независимых БЗ) и организация координационного управления с помощью введения звена КНВ существенно увеличивают число входных переменных и тем самым расширяют возможности учета параметров системы и объекта управления.

·       Минимальный расход полезного ресурса при формировании законов управления обеспечивается при использовании ИСУ на ОБЗ на квантовых вычислениях. Законы управления, сформированные ИСУ на ОБЗ на мягких вычислениях с разделенным управлением в условиях изменения параметров ОУ или внешних возмущающих воздействий, приобрели колебательный характер, а в законах управления, сформированных ИСУ на ОБЗ с одним НР, появились участки локально неустойчивых состояний. Наилучший показатель критерия качества «Сложность реализации управления» обеспечивается при использовании ИСУ на ОБЗ на квантовых вычислениях для всех рассмотренных типов корреляций по сравнению с ИСУ на ОБЗ на мягких вычислениях.

Таким образом, в работе рассмотрена ИСУ с применением технологий мягких и квантовых вычислений для задачи точного позиционного управления роботом-манипулятором с тремя степенями свободы. Проанализировано поведение моделей, приближенных к реальным условиям, а также физического ОУ.

Однако для разработчиков систем управления избыточными роботами-манипуляторами, помимо организации прямого управления положениями звеньев, важной задачей также является обеспечение дополнительного качества – реконфигурируемости (структурной адаптации) ОУ в зависимости от состояния окружающей среды (в том числе и динамически изменяющейся): решение задачи обратной динамики избыточного манипулятора, построение оптимальной траектории устройства захвата, обход препятствий и др.

Литература

1.     Черноусько Ф.Л., Болотник Н.Н., Градецкий В.Г. Манипуляционные роботы: Динамика, управление, оптимизация. М.: Наука, 1989. 368 c.

2.     Ульянов С.В., Литвинцева Л.В., Добрынин В.Н., Мишин А.А. Интеллектуальное робастное управление: технологии мягких вычислений. М.: ВНИИгеосистем, 2011. 408 c.

3.     Castillo O., Melin P., Pedrycz W. Soft computing for hybrid intelligent systems. Berlin, Springer, 2008, 448 p.

4.     Jang J.-S.R., Sun C.-T, Mizutani E. Neuro-Fuzzy and Soft Computing. Upper Saddle River, NJ, Prentice Hall, 1997, 614 p.

5.     Kaynak O., Zadeh L.A., Turksen B. and Rudas I.J. (Eds). Computational intelligence: Soft computing and fuzzy-neuro integration with applications. Berlin: Springer-Verlag (NATO ASI Series, Series F), 1998, vol. 162, 542 p.

6.     Николаева А.В., Ульянов С.В. Интеллектуальное управление роботом-манипулятором на основе мягких вычислений // Программные продукты и системы. 2013. № 4. С. 157–162.

7.     Литвинцева Л.В., Ульянов С.И., Ульянов С.В., Ульянов С.С. Квантовый нечеткий вывод для создания баз знаний в робастных интеллектуальных регуляторах // Изв. РАН. Теория и системы управления. 2007. № 6. C. 71–126.

8.     Nielsen M.A., Chuang I.L. Quantum computation and quantum information. UK, Cambridge: Univ. Press, 2000, 700 p.

9.     Chen G., Diao С. Mathematical Theory of Quantum Computation. NY, Chapman Hall CRC, 2013, 320 p.

10.  Yanofsky N.S., Mannucci M.A. Quantum Computing for Computer Scientists. Cambridge, Cambridge Univ. Press, 2008, 368 p.

11.  Jaeger G. Quantum Information: An overview. NY, Springer Verlag, 2007, 284 p.

12.  Henderson L.W. Means-plus-function claims (and new developments in patentability of pure algorithms). IEEE Antennas and Propagation Magazine. 1999, vol. 41, no. 5, pp. 130–132.

13.  Sanctuary B.C. Correlations in entangled states // arXiv. 2006. URL: http://arxiv.org/ftp/quant-ph/papers/0508/0508238.pdf (дата обращения: 31.07.2013).

14.  Николаева А.В., Ульянов С.В. Проектирование интеллектуальной системы управления роботом-манипулятором. Ч. 3: Моделирование и физический эксперимент на основе технологии квантовых вычислений // Системный анализ в науке и образовании. 2013. № 1. С. 1–25.

15.  Jozsa R., Linden N. On the role of entanglement in quantum computational speed-up. Proceeding of the Royal Society, 2003, vol. 459, no. 2036, pp. 2011–2032.

16.  Клышко Д.Н. Основные понятия квантовой физики с операциональной точки зрения // УФН, 1998. Т. 168. № 9. C. 975–1015.

17.  Khrennikov A. Representation of the Kolmogorov model having all distinguishing features of quantum probabilistic model. Physics Letters A, 2003, vol. 316, no. 5, pp. 279–296.

References

1.     Chernousko F.L., Bolotnik N.N., Gradeckiy V.G. Manipulation Robots: dynamics, control, optimization. Moscow, Nauka Publ., 1989, 368 p. (in Russ.).

2.     Ulyanov S.V., Litvintseva L.V., Dobrynin V.N., Mi- shin A.A. Intelligent robust control: soft computing technologies. Moscow, VNIIgeosistem Publ., 2011, 408 p. (in Russ.).

3.     Castillo O., Melin P., Pedrycz W. Soft computing for hybrid intelligent systems. Berlin, Springer Publ., 2008, 448 p.

4.     Jang J.-S.R., Sun C.-T, Mizutani E. Neuro-Fuzzy and Soft Computing. Upper Saddle River, NJ, Prentice Hall Publ., 1997, 614 p.

5.     Kaynak O., Zadeh L.A., Turksen B. and Rudas I.J. (Eds). Computational intelligence: Soft computing and fuzzy-neuro integration with applications. Berlin, Springer-Verlag Publ., NATO ASI Series, Series F, 1998, vol. 162, 542 p.

6.     Nikolaeva A.V., Ulyanov S.V. Intelligent control of a robot manipulator based on soft computing. Programmnye produkty i systemy [Software & Systems]. 2013, no. 4, pp. 150–155 (in Russ.).

7.     Litvintseva L.V., Ulyanov S.I., Ulyanov S.V., Ulya- nov S.S. Quantum fuzzy inference for knowledge base design in ro­bust intelligent controllers. Izvestiya RAN. Teoriya i systemy uprav­leniya [Journal of Computer and Systems Sciences International]. 2007, no. 6, pp. 71–126 (in Russ.).

8.     Nielsen M.A., Chuang I.L. Quantum computation and quantum information. UK, Cambridge, Univ. Press, 2000, 700 p.

9.     Chen G., Diao С. Mathematical Theory of Quantum Computation. NY, Chapman Hall CRC Publ., 2013, 320 p.

10.  Yanofsky N.S., Mannucci M.A. Quantum Computing for Computer Scientists. Cambridge, Cambridge Univ. Press, 2008, 368 p.

11.  Jaeger G. Quantum Information: an overview. NY, Springer Verlag Publ., 2007, 284 p.

12.  Henderson L.W. Means-plus-function claims (and new developments in patentability of pure algorithms). IEEE Antennas and Propagation Magazine. 1999, vol. 41, no. 5, pp. 130–132.

13.  Sanctuary B.C. Correlations in entangled states. 2006. Available at: http://arxiv.org/ftp/quant-ph/papers/0508/0508238.pdf (accessed 31 July 2013).

14.  Nikolaeva A.V., Ulyanov S.V. Intelligent control system of a robot manipulator. Pt. 3. Modeling and physical experiment based on quantum computing technology. Sistemny analiz v nauke i obrazovanii [System analysis in science and education]. 2013, no. 1, pp. 1–25 (in Russ.).

15.  Jozsa R., Linden N. On the role of entanglement in quantum computational speed-up. Proc. of the Royal Society. 2003, vol. 459, no. 2036, pp. 2011–2032.

16.  Klyshko D.N. Basic quantum mechanical concepts from the operational viewpoint. Physics-Uspekhi (Advances in Physical Sciences). 1998, vol. 41, no. 9, pp. 885–922 (in Russ.).

17.  Khrennikov A. Representation of the Kolmogorov model having all distinguishing features of quantum probabilistic model. Physics Letters A. 2003, vol. 316, no. 5, pp. 279–296 (in Russ.).