Программные продукты и системы

Задача синтеза топологической структуры магистральных сетей (МС) является одной из основных при проектировании магистральных телекоммуникационных сетей (ТКС) и состоит в выборе оптимальной схемы соединения узлов коммутации и концентрации, а также пропускной способности линий и оптимальных маршрутов передачи информации. Выбор топологической структуры может осуществляться по стоимостному критерию минимума суммарной годовой аренды каналов связи при наличии ограничений на время задержки и надежность передачи информации [1]. При разработке модели структурно-функ­ционального синтеза МС удобно использовать методы решения оптимизационных задач с помощью теории графов или сетей. Граф состоит из конечного множества вершин и множества ребер, соединяющих вершины (элементы системы). Для магистральных ТКС в качестве вершин графа выступают узлы коммутации, а ребрами являются соединяющие их магистральные каналы связи.

При формализованном описании элементов и структуры МС ее можно представить в виде неориентированного графа G=(Y, S), где Y={yi},  – множество узлов коммутации; S={sk},  – множество каналов связи между узлами; n – количество узлов; M – количество каналов. Вершины графа G=(Y, S) соответствуют узлам коммутации сети, ребра − каналам связи между узлами коммутации, а топология графа − топологической структуре МС. Выбор вида графа определен дуплексным режимом передачи по каналам связи между узлами коммутации. Тогда любая пара соседних вершин графа yi и yj (yiÎY, yjÎY, ) характеризуется расстоянием между ними dij, а D={dij} – это матрица расстояний графа G.

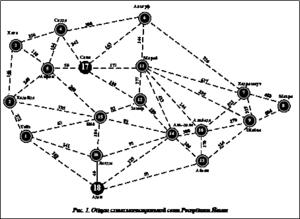
Рассмотрим общий граф МС Республики Йемен (рис. 1), на котором показаны места расположения узлов коммутации. Задача заключается в оптимальном подключении узлов коммутации для того, чтобы расстояния (пути прохождения информации) от любого узла коммутации до региональных узлов коммутации (17 и 18) были кратчайшими, то есть необходимо решить задачу топологического синтеза с выбором оптимальной схемы соединения узлов коммутации по расстоянию. Возможные магистральные каналы на рисунке 1 показаны штриховыми отрезками, числа над ними характеризуют расстояния между ма- гистральными узлами, узлы коммутации изображены темными, а региональные узлы коммутации – крупными темными кружками. Аналогичные обозначения применяются и на последующих рисунках. С учетом приведенных рассуждений и схемы МС матрица связности для рассматриваемой задачи будет состоять из узлов-источников i, узлов-адресатов j и матрицы расстояний между ними D={dij}.

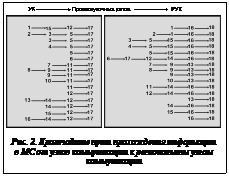
Граф МС как совокупность узлов коммутации и соединяющих их каналов связи в среде Matlab можно описать с помощью функции sparse. После этого задача синтеза МС Республики Йемен в соответствии с критерием расстояния может быть решена на основе методов теории графов с использованием функции graphshortestpath. С помощью этой функции можно находить кратчайшие пути по матрице расстояний dij между любой парой вершин, а также кратчайший маршрут между заданной парой вершин. Полученные оптимальные маршруты прохождения информации от любого узла коммутации к региональным узлам коммутации 17 (Сана) и 18 (Аден) приведены на рисунке 2.

При решении задачи с помощью graphshor­testpath получаем оптимальные маршруты прохождения информации от каждого узла коммутации до каждого регионального узла коммутации. В программе необходимо исключить повторяющиеся маршруты и учесть, что граф является неориентированным.

Результат синтеза структуры МС Республики Йемен с учетом общей схемы МС приведен на рисунке 3. На схему сплошными линиями нанесены полученные кратчайшие маршруты прохождения информации от узлов коммутации к региональным узлам коммутации, а пунктирными – исключенные линии связи. Полученная оптимальная топология МС Республики Йемен позволяет перейти к решению задачи параметрического синтеза МС, важнейшей частью которого является определение пропускной способности магистральных каналов связи.

Для синтеза пропускной способности каналов связи МС Республики Йемен необходимо знать пропускную способность каналов, соединяющих абонентов с узлами коммутации. При обмене информационными и служебными сообщениями между абонентами и региональными узлами коммутации информация передается таким образом, что абонент подключается к региональным узлам коммутации только через определенный узел коммутации, причем каждый абонент может соединяться только с одним узлом коммутации.

С учетом возможности подключения к узлам коммутации нескольких абонентов был произведен расчет суммарных информационных потоков gj, j=1, …, n, поступающих в МС. Для полученной структуры МС (рис. 3) задача оптимального прохождения информации от абонентов к региональ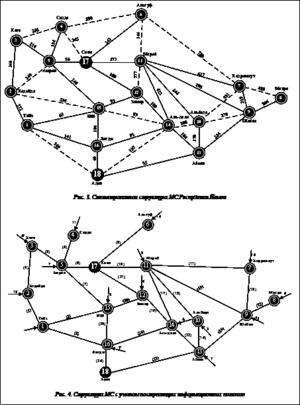ным узлам коммутации может быть представлена в виде, показанном на рисунке 4. Номера магистральных каналов приведены на рисунке в круглых скобках, а числа над стрелками показывают информационные потоки от абонентов к каждому узлу коммуникации.

Для решения поставленной задачи нахождения оптимальной пропускной способности магистральных каналов будем использовать рассмотренную в работе [2] модель МС с альтернативной маршрутизацией сообщений. Для МС, состоящей из n узлов коммутации и M каналов, с учетом возможности разделения каждого канала на m линий связи обозначим информационные потоки по каналам в виде jik, . Оптимизацию функционирования сети можно производить по критериям средней задержки сообщения T и максимальной загруженности T1 сети.

Сформулируем задачу оптимальной маршрутизации. По заданной топологической структуре информационной сети, значению входного потока g и матрице пропускной способности C1ik,  , необходимо найти оптимальные значения потоков ||jik||. Минимизацию можно производить по критериям T и T1:

,                              (1)

,       (2)

при выполнении следующих ограничений:

.                          (3)

Важно не допустить потери пакетов на сетевых узлах и в сети в целом, для этого необходимо обеспечить выполнение условий сохранения потока:

                       (4)

где E – множество каналов связи; i – узел-источ­ник; j – узел-адресат; l=i и l=j характеризуют соответственно узел-вход и узел-выход.

Изображенная на рисунке 4 МС Республики Йемен состоит из n=18 узлов и M=26 каналов связи. При условии формирования поступающей нагрузки в виде бесприоритетного трафика входные потоки от абонентов gj, , должны быть переданы через соответствующие узлы к региональным узлам коммутации. При этом необходимо минимизировать критерий (2) при выполнении ограничений (3) и (4). Для упрощения расчетов разделение по линиям связи не производится. В этом случае m=1, а рассмотренные матрицы потоков и пропускной способности являются одномерными массивами.

Задача оптимизации критерия (2) относится к классу задач нелинейной оптимизации функции нескольких переменных с ограничениями типа неравенств (3) и равенств (4) [3], и ее решение может быть получено в среде MatLab с помощью функции fmincon. При этом ограничения типа неравенств удобно задавать с помощью нижней и верхней границ lb, ub. При синтезе значений пропускной способности магистральных каналов для оптимальной передачи информационных сообщений по МС от узлов коммутации к региональным узлам коммутации для всех имеющихся каналов нижней границей является lb=0, а в качестве верхней границы можно взять максимальное из информационных потоков от абонентов значение ub=max{gi}, .

Для приведенной на рисунке 4 МС Республики Йемен условия сохранения потоков с учетом произведенной нумерации будут выглядеть следующим образом:

(5)

Равенства (5) описывают условия сохранения потоков в узлах коммутации, причем Fi=g для узла-входа; Fi=–g для узла-выхода; Fi=0, , для промежуточных узлов. Условия сохранения потоков в узлах маршрутизации (5) являются ограничениями типа равенств и при решении оптимизационной задачи в Matlab представляют матрицы Aeq, beq. Матрица Aeq постоянна и не зависит от номеров узла-входа и узла-выхода, так как характеризует проходящие через узел информационные потоки. Матрица beq зависит от номеров узла-входа и узла-выхода, соответствует Fi в уравнениях (5), и ее элементы равны gi для узла-входа; –gi для узла-выхода и 0 для промежуточных узлов.

Для решения задачи синтеза МС разработана программа direct.m, позволяющая найти оптимальные информационные потоки в магистральных каналах связи по критериям средней задержки сообщения T и максимальной загруженности сети T1. Начальное приближение разделения потоков может быть определено с помощью функции linprog при вышеуказанных граничных условиях. При передаче информации в МС от узлов коммутации к региональным узлам коммутации необходимо многократно решать оптимизационную задачу для узлов-входов узла коммутации  и узлов-выходов региональных узлов коммутации , где n1=2 – число региональных узлов коммутации (суперцентров) по критерию максимальной загруженности сети T1. При этом в качестве пропускной способности всех магистральных каналов берется max{gi}, .

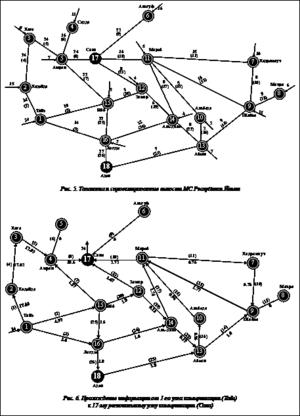
Для нахождения проектируемой пропускной способности МС используются полученные оптимальные информационные потоки jijk,  от каждого j-го узла коммутации к каждому k-му региональному узлу коммутации. В качестве оптимальных значений пропускной способности магистральных каналов нужно взять максимальные из полученных информационных потоков C1i=max{jijk},  Проверку спроектированных значений пропускной способности каналов МС можно произвести и по критерию средней задержки сообщения T, находя минимальное время передачи информации. Значения спроектированной по критерию средней задержки пропускной способности каналов C1i,  для МС Республики Йемен с учетом топологии сети приведены на рисунке 5 над номерами каналов (без скобок). Пример передачи информации при прохождении сообщения от 1-го узла коммутации (Тайз) к 17-му региональному узлу коммутации (Сана) приведен на рисунке 6.

Процесс, изображенный на рисунке 6, позволяет проследить пути прохождения информационных потоков от магистральных узлов к суперцентрам и подтверждает условия сохранения потоков для каждого узла коммутации. Таким образом, предложенная модель оптимального распределения потоков в информационной сети позволяет на основе численных оптимизационных методов для произвольных топологии сети и количества каналов связи произвести оптимизацию по критериям средней задержки и максимальной загруженности сети. Она учитывает условия сохранения потоков для промежуточных узлов сети. Оптимизация по критерию максимальной загруженности позволяет обеспечить наиболее сбалансированную загруженность каналов ТКС и повысить качество обслуживания.

Литература

1.     Вишневский В.М. Теоретические основы проектирования компьютерных сетей. М.: Техносфера, 2003. 506 с.

2.     Дмитриев Г.А., Марголис Б.И., Музанна М.М. Решение задачи оптимальной маршрутизации по критерию загруженности сети // Программные продукты и системы. 2013. № 4. С. 173–176.

3.     Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах. М.: Высш. школа, 2005. 544 с.

References

1.     Vishnevskiy V.M. Teoreticheskie osnovy proyektirovaniya kompyuternykh setey [Theoretical basics of computer network design]. Moscow, Tekhnosfera Publ., 2003, 506 p.

2.     Dmitriyev G.A., Margolis B.I., Muzanna M.M. Optimal routing using the network congestion criterion. Programmnye pro­dukty i sistemy [Software & Systems]. 2013, no. 4, pp. 173–176.

3.     Panteleev A.V., Letova T.A. Metody optimizatsii v prime­rakh i zadachakh [Optimization methods in examples and exercises]. Moscow, Vyssh. shkola Publ., 2005, 544 p.