Как известно, любое нетривиальное ПО после этапа разработки содержит ошибки. Проверка современного ПО, состоящего из громадного количества строк кода, не представляется возможной. В связи с этим широко распространен подход, при котором реальные системы представляются в виде моделей, верифицируемых при помощи специализированного ПО. Модельный подход подразумевает частичную верификацию, которая может быть направлена на проверку наиболее существенных свойств, абстрагировавшись от менее важных деталей системы. Таким образом, вери- фикация моделей не позволяет в общем случае гарантировать отсутствие ошибок в реальной системе. По этой причине после этапа верификации модели необходим этап тестирования исходной системы в реальных условиях.
Для представления моделей технических систем авторы статьи используют язык асинхрон- ных функциональных схем (АФС) [1], в котором программе в качестве семантического значения сопоставляется множество вычислительных последовательностей (ВП) (путей) выполнения распределенной АФС-программы. Далее семантическое значение представляется в виде системы рекурсивных уравнений [1]. Полученная система является удобной формой представления семантических значений программ для анализа различных свойств программ.
Для создания автоматизированных програм- мных средств проверки моделей необходимы формальные методы верификации. Одним из них является метод, использующий темпоральную логику линейного времени (linear-time temporal logic – LTL) [2]. В этом методе техническая система, представленная в виде структуры Крипке [2], и отрицание проверяемого свойства преобразуются в автоматы Бюхи [2]. Далее по ним строится композиция автоматов для проверки выполнимости проверяемого свойства на технической системе.
В данной статье предложен метод, при котором системы рекурсивных уравнений, полученные из исходных АФС-программ, непосредственно представляются в виде автоматов Бюхи, что позволяет использовать описанный выше подход. Предложенный метод имеет преимущество над указанным выше методом, заключающееся в том, что нет необходимости в проведении дополнительного этапа преобразования системы рекурсивных уравнений в структуру Крипке.
Язык АФС
В языке АФС программы представляются как функции, взаимодействующие посредством интерфейса в виде каналов.
Множество АФС-программ Prog с типичным элементом pr определяется следующим образом:
pr ::= NET {can} BEGIN fproc END
can ::= CHAN j::type(k):type(l) | can1 ; can2
type ::= ALL | ANY
fproc ::= FUN i::c | fproc1 ; fproc2
c ::= a | skip | exit | break | wait(time) | read(i, l) | write(i, k) | SEQ(c {, c}) |
PAR(c {, c}) | ALT(gc) | LOOP(ALT(gc))
gc ::= g ® c | gc {; gc}
g ::= tt | ff | b | wait(time) | read(i, l) | write(i, k)
Неформально семантические конструкции языка АФС можно описать так:
– под элементарной командой a понимается обычное присваивание;
– пустая команда skip не приводит к выполнению каких-либо действий;
– выполнение команды exit приводит к завершению функционального процесса;
– выполнение команды break приводит к завершению выполнения цикла;
– команда wait(time) задерживает выполнение функционального процесса на время, задаваемое выражением time;
– команда чтения read(i, l) осуществляет запрос на прием данных из l-го выхода i-го канала, а команда write(i, k) – запрос на передачу данных на k-й вход i-го канала; если l-й выход (k-й вход) канала i готов к выдаче (приему) данных, то осуществляется чтение данных из канала (запись данных в канал), после чего функциональный процесс продолжается; в противном случае выполнение функционального процесса задерживается;
– команда SEQ(c{, c}) означает последовательное выполнение команд, перечисленных внутри скобок;
– параллельная команда PAR(c{, c}) означает параллельное выполнение команд, перечисленных внутри скобок;
– защищенная команда g®c может выполняться лишь в случае истинности защиты g; значение защиты g является истинным в следующих случаях: 1) g≡tt; 2) g≡b, причем значение b есть истина; 3) g≡wait(time) через интервал времени, задаваемый выражением time; 4) g≡read(i, l) либо g≡write(i, l) и соответствующий выход (вход) канала i готов к обмену; в последнем случае, если канал i не готов к обмену, выполнение защищенной команды приостанавливается;
– альтернативная команда ALT(gc{; gc}) означает выполнение одной из защищенных команд, перечисленных в скобках, для которой значения защит являются истинными;
– команда цикла LOOP(ALT(gc{; gc})) означает многократное выполнение альтернативной команды; завершение цикла осуществляется, если все защиты ALT-команды являются булевскими выражениями и ни одно из значений защит не является истинным либо при выполнении команды break;
– канал типа ALL(k):ALL(l) вначале принимает данные по всем своим k входам, после чего он становится готовым для передачи данных по всем l выходам; канал освобождается (и становится готовым для приема новых данных) после передачи данных по всем своим выходам;
– канал типа ALL(k):ANY(l) аналогичен по входу каналу типа ALL(k):ALL(l); канал освобождается после передачи данных по любому из своих выходов;
– канал типа ANY(k):ALL(l) становится готовым для передачи данных, если он принял данные по одному из входов, и освобождается после передачи данных по всем своим выходам;
– канал типа ANY(k):ANY(l) становится готовым для передачи данных, если он принял данные по одному из входов, и освобождается после передачи данных по любому из своих выходов.
Формализация семантики АФС-программ. Зададим вначале априорную семантику функциональных процессов, то есть семантику функ- циональных процессов без учета их взаимодействия друг с другом. Семантическая функция имеет вид  :FProc→SP, где FProc – множество функциональных процессов с типичным элементом fproc, SP – множество всех подмножеств ВП:
:FProc→SP, где FProc – множество функциональных процессов с типичным элементом fproc, SP – множество всех подмножеств ВП:
 ⟦fproc1;frpoc2⟧=
⟦fproc1;frpoc2⟧= ⟦fproc1⟧‖
⟦fproc1⟧‖ ⟦frpoc2⟧
⟦frpoc2⟧
 ⟦FUN i∷c⟧=
⟦FUN i∷c⟧= ⟦c⟧,
⟦c⟧,
где  :Cmd→SP – функция, сопоставляющая командам языка АФС множества ВП:
:Cmd→SP – функция, сопоставляющая командам языка АФС множества ВП:
 ⟦a⟧=A
⟦a⟧=A
 ⟦skip⟧=τ
⟦skip⟧=τ
 ⟦exit⟧=EXIT
⟦exit⟧=EXIT
 ⟦break⟧=BREAK
⟦break⟧=BREAK
 ⟦wait(time)⟧=TIME
⟦wait(time)⟧=TIME
 ⟦read(i, l)⟧=IN(i, l)
⟦read(i, l)⟧=IN(i, l)
 ⟦write(i, k)⟧=OUT(i, k)
⟦write(i, k)⟧=OUT(i, k)
 ⟦SEQ(c1; c2)⟧=
⟦SEQ(c1; c2)⟧= ⟦c1⟧∘
⟦c1⟧∘ ⟦c2⟧
⟦c2⟧
 ⟦PAR(c1; c2)⟧=
⟦PAR(c1; c2)⟧= ⟦c1⟧⫫
⟦c1⟧⫫ ⟦c2⟧
⟦c2⟧
 ⟦ALT(c1; c2)⟧=
⟦ALT(c1; c2)⟧= ⟦c1⟧+
⟦c1⟧+ ⟦c2⟧
⟦c2⟧
 ⟦tt→c⟧=E⟦tt⟧^
⟦tt→c⟧=E⟦tt⟧^ ⟦c⟧
⟦c⟧
 ⟦tt→c⟧=E⟦ff⟧^
⟦tt→c⟧=E⟦ff⟧^ ⟦c⟧
⟦c⟧
 ⟦tt→c⟧=E⟦b⟧^
⟦tt→c⟧=E⟦b⟧^ ⟦c⟧
⟦c⟧
 ⟦wait(time)→c⟧=
⟦wait(time)→c⟧= ⟦wait(time)⟧^
⟦wait(time)⟧^ ⟦c⟧
⟦c⟧
 ⟦read(i, l)→c⟧=
⟦read(i, l)→c⟧= ⟦read(i, l)⟧^
⟦read(i, l)⟧^ ⟦c⟧
⟦c⟧
 ⟦write(i, l)→c⟧=
⟦write(i, l)→c⟧= ⟦write(i, l)⟧^
⟦write(i, l)⟧^ ⟦c⟧
⟦c⟧
 ⟦LOOP(ALT(gc))→c⟧=(
⟦LOOP(ALT(gc))→c⟧=( ⟦ALT(gc)⟧)+
⟦ALT(gc)⟧)+
Определим семантическую функцию для выражений E:Exp→SP:
E⟦tt⟧=T
E⟦ff⟧=F
E⟦b⟧=B
где «∘» и «^» – операции последовательной композиции ВП.
Определение 1. ВП cp называется пустой и обозначается через ԑ, если
1) cp≡t,
2) cp≡T^ԑ.
Бесконечную последовательность вида ԑw обозначим через ω (зацикливание).
Определение 2. ԑÎsp, если
1) sp≡e,
2) sp=sp1+sp2 и ԑ принадлежит хотя бы одному из множеств – sp1 или sp2,
3) sp=sp1∘sp2 и ԑ принадлежит и sp1, и sp2 одновременно.
Выражение sp+ есть минимальная фиксированная точка оператора F(sp), то есть sp+=μF(sp). Оператор F(sp) имеет вид: F(sp)=λq. ∘q+ν, где
∘q+ν, где 


В последнем определении символ ∆ обозначает выражение, значение которого зависит от среды, где вычисляется ∆. Выражение ∆ может принимать одно из двух значений: t или Æ. Вычисление значения ∆ откладывается, как правило, до момента построения семантического значения всей программы целиком на основе семантических значений компонентов этой программы.
Каналам в качестве семантических значений сопоставляются множества ВП. Каналы можно рассматривать как процессы специального вида – канальные процессы.
Канал связи интерпретируется как циклический процесс, который вначале принимает данные от функциональных процессов, а затем, когда все необходимые данные от функциональных процессов (в соответствии с логикой входов этого канала) уже приняты, передает данные функциональным процессам (в соответствии с логикой выходов канала).
В отличие от функциональных процессов выход из канального процесса (завершение циклического процесса) невозможен. Завершение АФС-программы происходит при переходе всех функциональных процессов в пассивное состояние.
Семантическая функция каналов  :Can→SP (Can – множество каналов связи с типичным элементом сan) имеет вид
:Can→SP (Can – множество каналов связи с типичным элементом сan) имеет вид
 ⟦ CHAN j∷type1(k) : type2(l)⟧=((type1(IN(j, 1),
⟦ CHAN j∷type1(k) : type2(l)⟧=((type1(IN(j, 1),
…, IN(j, k)))∘(type2 (OUT(j, 1), …, OUT(j, l) )))+.
Параметр type может принимать одно из двух значений: ALL или ANY.
ALL(X1, …, X2)=X1⫫X2⫫…⫫Xn, где операция ⫫ определяется следующим образом: X⫫Y=X⌊Y+Y⌊X.
Выражение X⌊Y означает то же, что и X||Y, за исключением того, что первым шагом будет действие из X.
Выражение p+ есть минимальная фиксированная точка оператора F'(p)=λq.p∘q.
Для наглядности восприятия ВП используем надстрочные индексы для значений IN (OUT), характеризующих ввод (вывод) информации в канал связи, тогда как подстрочные индексы используются для значений команд ввода (вывода) информации в функциональный процесс. Первый индекс в обоих случаях указывает номер канала, второй – номер входа (выхода) канала, по которому осуществляется ввод (вывод) информации.
Для определения взаимодействия компонентов программы зададим частично определенную функцию

Семантическую функцию для АФС-программ обозначим как  :Prog→SP. Так, например, если АФС-программа имеет вид
:Prog→SP. Так, например, если АФС-программа имеет вид
pr=NET can1; can2; …; canm
BEGIN fproc1;fproc2;…;fprocn END,
то  ⟦pr⟧=
⟦pr⟧= ⟦can1⟧ ∥
⟦can1⟧ ∥ ⟦can2⟧∥⋯∥
⟦can2⟧∥⋯∥ ⟦canm⟧∥
⟦canm⟧∥  ⟦fproc1⟧ ∥
⟦fproc1⟧ ∥ ⟦fproc2⟧∥⋯∥
⟦fproc2⟧∥⋯∥ ⟦fprocn⟧.
⟦fprocn⟧.
Для построения системы рекурсивных уравнений, характеризующих семантическое значение программы, можно строить систему уравнений либо по выражению для  ⟦pr⟧, задающему семантическое значение всей программы целиком, либо на базе множества систем уравнений, характеризующих априорные семантические значения для составляющих компонентов АФС-программы, в частности для каждого функционального процесса и канала связи в отдельности.
⟦pr⟧, задающему семантическое значение всей программы целиком, либо на базе множества систем уравнений, характеризующих априорные семантические значения для составляющих компонентов АФС-программы, в частности для каждого функционального процесса и канала связи в отдельности.
Пример 1. Рассмотрим АФС-программу pr, моделирующую задачу производитель–потребитель:
NET
CHAN1∷ALL(1):ALL(1)
BEGIN
FUN2∷LOOP(ALT(b →SEQ(write(1,1);a1)))
FUN3 ∷LOOP(ALT(read(1,1)→a2))
END
Из данной АФС-программы получаем семантическое значение
 ⟦ FUN2 ∷ LOOP(ALT(b→SEQ(write(1,1);a1)))⟧=
⟦ FUN2 ∷ LOOP(ALT(b→SEQ(write(1,1);a1)))⟧=
=(B^OUT1,1∘A1)+
 ⟦ FUN3 ∷ LOOP(ALT(read(1,1)→a2)) ⟧ = (IN1,1^A2)+
⟦ FUN3 ∷ LOOP(ALT(read(1,1)→a2)) ⟧ = (IN1,1^A2)+
F⟦ CHAN1∷ALL(1):ALL(1) ⟧ = (IN1,1 ∘ OUT1,1 )+
 ⟦pr⟧=P2‖P3‖ K1=
⟦pr⟧=P2‖P3‖ K1=
=(B^OUT1,1∘A1)+‖(IN1,1^A2)+‖(IN1,1∘OUT1,1 )+.
Полученное семантическое значение может быть представлено системой рекурсивных уравнений [1].
Обозначая элементы семантической области метапеременными X, Y, Z, опишем свойства семантической области с помощью следующих схем аксиом:
|
X+X=X
X+Y=Y+X
X+(Y+Z)=(X+Y)+Z
(X+Y)∘Z=X∘Z+Y∘Z
(X∘Y)∘Z=X∘(Y∘Z)
τ∘X=X
X∘τ=X
ω ∘X= ω
∅∘X=∅
X+∅=X
(β^X)∘Y=β^(X∘Y)
F^X=∅
∅^X=∅
|
X‖(Y||Z)=(X||Y)||Z
X‖Y=X ⌊ Y+Y ⌊ X+ X | Y
d1' | d2'=C(d1',d2')
α1 | (α2∘X) = ( α1 | α2 ) ∘ X, если α2 ≠ τ
(α1 ∘ X) | (α2 ∘ Y) = (α1 | α2) ∘ (X ‖ Y), если α1 ≠ τ, α2 ≠ τ
α | (β^X) = (α | β)^X
(α ∘ X) | (β ^ Y) = (α | β)^(X ‖ Y), если α≠τ
(β1 ^ X) | (β2 ^ Y) = (β1 | β2 ) ^ (X ‖ Y)
(X+Y)| Z=(X│Z)+ (Y|Z)
τ ∘ X | Y = X | Y
X | Y = Y |X
α⌊X = α∘X
α∘X⌊Y = α ∘ (X‖Y), если α≠τ
(β^X) ⌊Y = β^(X‖Y)
τ ∘ X ⌊Y = X ⌊Y
(X+Y)⌊Z = X ⌊Z+Y⌊Z
(X | Y)⌊Z = X |(Y⌊Z)
(X ⌊ Y)⌊Z = X ⌊(Y ‖Z)
X‖Y = X ⌊ Y+Y ⌊ X+ X | Y
|
где Æ – останов, β – тест, ω – зацикливание.
Пример 2. Представим полученное выше семантическое значение АФС-программы в виде системы рекурсивных уравнений:
P1=B^P2+T^P3
P2=γ1,1∘P4
P3=Æ
P4=A1∘P5+γ1,1^P6
P5=B^P7+T^P8+γ1,1^P9
P6=A1∘P9+A2∘P10
P7=γ1,1∘P11
P8=γ1,1∘P12
P9=B^P11+T^P12+A2∘P1
P10=A1∘P1
P11=γ1,1∘P13+A2∘P2
P12=A2∘P3
P13=A1∘P14+A2∘P4
P14=B^P15+T^P16+A2∘P5
P15=γ1,1∘P6+A2∘P7
P16=A2∘P8.
Автоматы Бюхи
Семантические значения, представленные в виде системы рекурсивных уравнений, могут быть заданы с помощью автомата Бюхи [2].
Автомат Бюхи – это пятерка (S, Σ, S0, δ, F), где Σ – конечное множество символов (алфавит); S –множество состояний; S0⊆S – множество начальных состояний (содержащее только один элемент для детерминированного случая); δ : S×Σ→2s – отношение переходов (для детерминированного автомата δ:S×Σ→S); F⊆S – множество финальных состояний.
Автомат Бюхи принимает слово, если при чтении этого бесконечного слова автомат проходит бесконечное количество раз хотя бы одно финальное состояние.
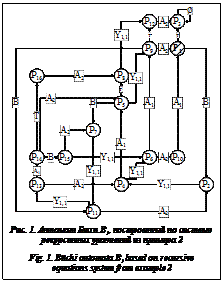 Пример 3. Представим полученную в примере 2 систему рекурсивных уравнений (предварительно представив уравнение P3=Æ в виде P3=Æ∘P3) в виде автомата Бюхи B1 (рис. 1). Множество начальных состояний автомата B1 включает одно состояние P1, выделенное на рисунке 1 штриховкой c наклоном вправо.
Пример 3. Представим полученную в примере 2 систему рекурсивных уравнений (предварительно представив уравнение P3=Æ в виде P3=Æ∘P3) в виде автомата Бюхи B1 (рис. 1). Множество начальных состояний автомата B1 включает одно состояние P1, выделенное на рисунке 1 штриховкой c наклоном вправо.
Описание свойств с помощью LTL-формул
Для проверки вычислимости тех или иных свойств будем описывать эти свойства в виде формул LTL [2].
Формулы LTL – это атомарный предикат p, q, …, или формулы LTL, связанные логическими операторами ∨, ¬, или формулы LTL, связанные темпоральными операторами U, X.
Формально формулы LTL задаются грамматикой φ=p|¬φ|φ∨φ|Xφ|φUφ.
Истинность формулы φ логики LTL на вычислении s=s0, s1, … определяется индуктивно по формуле φ:
– σ⊨p, если атомарный предикат p истинен в начальном состоянии вычисления σ;
– σ⊨¬φ, если формула φ не истинна на σ;
– σ⊨φ1∨φ2≡σ⊨φ1∨σ⊨φ2, если на σ выполняется или φ1, или φ2;
– σ⊨Xφ≡σ1⊨φ, если φ выполняется на вычислении σ1=s1, s2, …;
– σ⊨φ1Uφ2, если когда-то в будущем состоянии вычисления σ выполнится формула φ2, а до ее выполнения во всех состояниях вычисления σ будет выполняться φ1;
– σ⊨Fφ≡trueUφ≡(∃ k≥0) sk⊨φ, если найдется такое k, что φ выполняется на вычислении sk=sk, s(k+1), …;
– σ⊨Gφ≡¬F¬φ≡(∀ k≥0) sk⊨φ, если φ выполняется на всех состояниях вычисления σ.
Любая формула LTL φ на конкретном вычислении будет либо истинной, либо ложной.
Вычисление – это бесконечная последовательность состояний, которые система проходит во времени.
 Обозначим через σ(i) состояние si вычисления σ, а σi – вычисление, начиная с si, то есть σi=si, si+1, …. Тогда si⊨φ обозначает утверждение, что в состоянии si выполняется формула φ, а σ⊨φ – что на вычислении σ выполняется формула φ. При этом полагается, что формула выполняется на вычислении σ, если она истинна в начальном состоянии последовательности σ.
Обозначим через σ(i) состояние si вычисления σ, а σi – вычисление, начиная с si, то есть σi=si, si+1, …. Тогда si⊨φ обозначает утверждение, что в состоянии si выполняется формула φ, а σ⊨φ – что на вычислении σ выполняется формула φ. При этом полагается, что формула выполняется на вычислении σ, если она истинна в начальном состоянии последовательности σ.
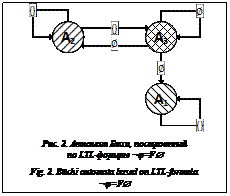
Пример 4. Для проверки выполнимости свойства безопасности (типичный пример свойства безопасности – свобода от блокировок) φ=G¬Æ на системе рекурсивных уравнений из примера 2 построим (согласно алгоритму, представленному в [2]) автомат B¬φ (рис. 2) для формулы ¬φ=FÆ. Обозначим через cl(φ) множество всех подформул формулы φ. Множество подформул формулы φ называется согласованным, если существует вычисление, на котором все они могут выполняться. Атомы формулы φ – это максимальные множества согласованных формул из cl(φ), которые могут помечать состояния вычислений [2]. Атомы можно считать состояниями искомого автомата Бюхи. Таким образом, в соответствии с правилами, описанными в [2], множество состояний автомата B¬φ составляют три атома: A1={}, A2={FÆ} и A3={Æ, FÆ}. Множество начальных состояний S0 состоит из двух состояний – A2 и A3, так как именно атомы A2 и A3 включают формулу FÆ. Множество финальных состояний включает два состояния – A1 и A3. Финальные состояния автомата B¬φ (рис. 2) заштрихованы с наклоном влево. Таким образом, состояние A3, которое является как начальным, так и финальным, выделено на рисунке 2 двойной штриховкой. Алфавит S автомата B¬φ состоит из двух символов – Æ и {}, где символ {} означает отсутствие символа Æ, то есть если переход помечен символом {}, значит, переход выполняется по любому символу, отличному от Æ. Переходы формируются в соответствии с правилами, описанными в [2].
Алгоритм проверки выполнимости LTL-формул для АФС-программ
 Для проверки выполнимости LTL-формулы на системе рекурсивных уравнений будем использовать следующий алгоритм.
Для проверки выполнимости LTL-формулы на системе рекурсивных уравнений будем использовать следующий алгоритм.
1. Представим модель технической системы в виде автомата Бюхи B.
2. В соответствии с алгоритмом, описанным в [2], построим по LTL-формуле ¬φ контрольный автомат Бюхи B¬φ.
3. Согласно [2] построим синхронную композицию автоматов B⊗ B¬φ. (Так же, как для конечных автоматов, синхронная композиция автоматов Бюхи – это автомат B¬φ, стоящий рядом с B и перехватывающий все входы и выходы автомата B. Автомат B¬φ выступает в роли контрольного автомата, работающего совместно и синхронно с B.) Синхронная композиция автоматов B⊗B¬φ допускает пересечение языков L и L¬φ, допускаемых соответственно автоматами B и B¬φ. Следовательно, если язык, допускаемый автоматом B⊗B¬φ, не пуст, значит, автомат B допускает ошибочное слово из языка L¬φ.
4. Проверим композицию автоматов B⊗B¬φ на наличие цикла, достижимого из начального состояния и включающего финальное состояние. Если такой цикл имеется, значит, формула ¬φ выполняется хотя бы на одном вычислении автомата Бюхи B, следовательно, формула φ не выполняется на автомате Бюхи B.
Пример 5. Построим синхронную композицию автоматов B1⊗B¬φ (рис. 3) для пары начальных состояний P1 и A2 из автоматов B1 (см. пример 3) и B¬φ (см. пример 4) соответственно. Если невыполнимость формулы φ на автомате B1⊗B¬φ по- казать не удастся, построим синхронную композицию автоматов B1⊗B¬φ для пары начальных состояний P1 и A3. Финальными состояниями автомата B1⊗B¬φ являются такие пары состояний PB1, AB¬φ, в которых AB¬φ – финальное состояние автомата B¬φ.
В композиции автоматов B1⊗B¬φ имеется цикл (переходы, демонстрирующие наличие цикла, выделены жирной линией), достижимый из начального состояния и проходящий финальное состояние (P3, A3). Следовательно, формула ¬φ выполняется хотя бы на одном вычислении автомата B1, что означает невыполнимость формулы φ на исходном автомате B1. Отсюда следует, что в исходной программе существует возможность блокировки.
В заключение отметим, что в статье показан метод верификации выполнимости различных временных свойств в технических системах, представленных в виде АФС-программ. В предложенном методе осуществляется непосредственно преобразование семантического значения АФС-программы в автомат Бюхи, что, на взгляд авторов, является более естественным и понятным представлением технических систем по сравнению с их представлениями в виде структур Крипке.
Литература
1. Кораблин Ю.П. Семантика языков распределенного программирования. М.: Изд-во МЭИ, 1996. 102 с.
2. Карпов Ю.Г. Model Checking. Верификация параллельных и распределенных программных систем. СПб: БХВ-Петербург, 2010. 260 с.
3. Кораблин Ю.П., Кучугуров И.В., Косакян М.Л. Вопросы эквивалентности схем параллельных программ // Программные продукты и системы. 2011. № 4. С. 66–72.
4. Кораблин Ю.П., Косакян М.Л., Кучугуров И.В. Вопросы взаимодействия и синхронизации распределенных программ на С++ с использованием Win API // Ученые записки РГСУ. 2013. № 1. С. 104–112.
5. Кларк Э.М., Грамберг О., Пелед Д. Верификация моделей программ: Model Checking. М.: Изд-во МЦНМО, 2002. 416 с.
6. Emerson E.A. Temporal and modal logic. In: J. van Leeuwen, ed. Handbook of Theoretical Computer Science, 1990, vol. B, pp. 995–1072.
7. Giannakopoulou D., Lerda F. Efficient translation of LTL formulae into Buchi automata. NASA Ames Research Ceter, TR, 2001, 17 p.
8. Bruns G., Godefroid P. Temporal Logic Query-Checking. Proc. 16th Ann. IEEE Symp. Logic in Computer Science, 2001, pp. 898–914.
9. Alur R., Dill D., Automata for modeling real-time system LNCS. Springer-Verlag, 1990, vol. 443, pp. 322–335.
References
1. Korablin Yu.P. Semantika yazykov raspredelennogo programmirovaniya [Semantics of distributed programming languages]. Moscow, MEI Publ., 1996, 102 p.
2. Karpov Yu.G. Model Checking. Verifikatsiya parallelnykh i raspredelyonnykh programmnykh sistem [Model Checking. Verification of parallel and distributed programm systems]. St. Petersburg, BHV-Peterburg Publ., 2010, 260 p.
3. Korablin Yu.P., Kuchugurov I.V., Kosakyan M.L. Issues of parallel programs schemes equivalence. Programmnye produkty i sistemy [Software & Systems]. 2011, no. 4, pp. 66–72
4. Korablin Yu.P., Kosakyan M.L., Kuchugurov I.V. Issues of interaction and synchronization of distributed programs on C++ using Win API. Uchenye zapiski RGSU [RSSU Proceedings]. 2013, no. 1, pp. 104–112.
5. Clarke E.M., Grumberg O., Peled D.A. Model Checking. The MIT Press, 1999, 314 p. (Russ. ed. Clarke E.M., Grumberg O., Peled D.A. Moscow, Moscow Center for Continuons Mathematical Education, 2002, 416 p.).
6. Emerson E.A. Temporal and modal logic. Handbook of Theoretical Computer Science (ed. J. van Leeuwen). 1990, vol. B, pp. 995–1072.
7. Giannakopoulou D., Lerda F. Efficient translation of LTL formulae into Buchi automata. NASA Ames Research Center, TR, 2001, 17 p.
8. Bruns G., Godefroid P. Temporal Logic Query-Checking. Proc. 16th Ann. IEEE Symp. Logic in Computer Science. 2001, pp. 898–914.
9. Alur R., Dill D. Automata for modeling real-time system. LNCS. Springer-Verlag Publ., 1990, vol. 443, pp. 322–335.

 :FProc→SP, где FProc – множество функциональных процессов с типичным элементом fproc, SP – множество всех подмножеств ВП:
:FProc→SP, где FProc – множество функциональных процессов с типичным элементом fproc, SP – множество всех подмножеств ВП: ⟦fproc1;frpoc2⟧=
⟦fproc1;frpoc2⟧= ⟦fproc1⟧‖
⟦fproc1⟧‖ ⟦c⟧,
⟦c⟧, :Cmd→SP – функция, сопоставляющая командам языка АФС множества ВП:
:Cmd→SP – функция, сопоставляющая командам языка АФС множества ВП: ⟦a⟧=A
⟦a⟧=A ∘q+ν, где
∘q+ν, где 

 :Can→SP (Can – множество каналов связи с типичным элементом сan) имеет вид
:Can→SP (Can – множество каналов связи с типичным элементом сan) имеет вид ⟦ CHAN j∷type1(k) : type2(l)⟧=((type1(IN(j, 1),
⟦ CHAN j∷type1(k) : type2(l)⟧=((type1(IN(j, 1),
 :Prog→SP. Так, например, если АФС-программа имеет вид
:Prog→SP. Так, например, если АФС-программа имеет вид ⟦pr⟧=
⟦pr⟧= Пример 3. Представим полученную в примере 2 систему рекурсивных уравнений (предварительно представив уравнение P3=Æ в виде P3=Æ∘P3) в виде автомата Бюхи B1 (рис. 1). Множество начальных состояний автомата B1 включает одно состояние P1, выделенное на рисунке 1 штриховкой c наклоном вправо.
Пример 3. Представим полученную в примере 2 систему рекурсивных уравнений (предварительно представив уравнение P3=Æ в виде P3=Æ∘P3) в виде автомата Бюхи B1 (рис. 1). Множество начальных состояний автомата B1 включает одно состояние P1, выделенное на рисунке 1 штриховкой c наклоном вправо. Обозначим через σ(i) состояние si вычисления σ, а σi – вычисление, начиная с si, то есть σi=si, si+1, …. Тогда si⊨φ обозначает утверждение, что в состоянии si выполняется формула φ, а σ⊨φ – что на вычислении σ выполняется формула φ. При этом полагается, что формула выполняется на вычислении σ, если она истинна в начальном состоянии последовательности σ.
Обозначим через σ(i) состояние si вычисления σ, а σi – вычисление, начиная с si, то есть σi=si, si+1, …. Тогда si⊨φ обозначает утверждение, что в состоянии si выполняется формула φ, а σ⊨φ – что на вычислении σ выполняется формула φ. При этом полагается, что формула выполняется на вычислении σ, если она истинна в начальном состоянии последовательности σ.