Система типового контроля программ на языке функционального программирования FPTL
| Бочаров И.А. (bocharovia@gmail.com) - Национальный исследовательский университет «Московский энергетический институт», Москва (магистрант), Москва, Россия, Кутепов В.П. (vkutepov@appmat.ru) - Национальный исследовательский университет «Московский энергетический институт», Москва, Москва, Россия, доктор технических наук, Шамаль П.Н. (sti0cli@gmail.com) - Национальный исследовательский университет «Московский энергетический институт», Москва (аспирант ), Москва, Россия | |
| Ключевые слова: типовой контроль, параллельные вычисления, функциональные языки программирования |
|
| Keywords: type checking, parallel computing, functional programming languages |
|
|
|
|
Язык FPTL (functional parallel typified language) создавался с целью эффективного параллельного выполнения функциональных программ на компьютерных системах с общей памятью. В отличие от известных языков функционального программирования, таких как LISP [1], ML [2], Haskell [3, 4], которые в большей степени основаны на лямбда-исчислении [5], FPTL базируется на модели построения новых функций путем применения операций композиции функций и общей формы их задания в виде систем функциональных уравнений. Язык рекурсивных функций [6] – очевидный пример такого подхода к заданию вычислимых функций. Кажущееся преимущество лямбда-основанных функциональных языков, обычно формулируемое как единообразный способ задания функций высших порядков, компенсируется в FPTL использованием в задании функций функциональных параметров. Этот традиционный способ повышения порядка функции допускает возможность в подставленной вместо функционального параметра функции снова использовать функциональные параметры, увеличивая таким образом функциональную иерархию в построении функций. Однако FPTL имеет ряд преимуществ перед основанными на лямбда-исчислении функциональными языками. Наиболее важными на практике являются следующие его особенности: - очевидная близость используемой нотации к традиционной математической форме задания функций; - алгебраизированная форма задания функции, позволяющая извлекать ее композиционную структуру (схему функции), что существенно улучшает проектирование, анализ и эквивалентные преобразования функций [7–9]; - возможность явного отражения и варьирования параллелизма в функциональной программе, поскольку три из четырех операций композиции являются параллельными; - простой алгоритм обнаружения параллелизма при выполнении, что позволяет исключить необходимость явного указания с помощью соответствующих процессных примитивов (как, например, в Haskell [4]), какие фрагменты программы могут выполняться параллельно; - простота в освоении; язык позволяет широко использовать библиотеки, как правило, оптимизированных функций, вводить абстрактные типы данных, использовать разработанные для него приложения для оценки сложности параллельного выполнения программы, приведения ее к оптимальной параллельной форме, анализа структурной сложности программ [10] и др. Одна из последних реализаций языка FPTL [11] была недостаточно эффективной, так как выполнялась на компьютерах с распределенной памятью (многоядерные компьютеры в то время еще не были широко распространены). Реализация FPTL на многоядерных компьютерах, напротив, оказалась успешной. Это подтверждают приведенные в [12] экспериментальные данные ускорения FPTL-программ. В данной реализации, которая базируется на принципе интерпретации программы и динамическом выявлении и регулировании зернистости параллелизма и выполнена с использованием нитевого процессного параллелизма, можно достигать заметного ускорения при выполнении FPTL-программ [12]. FPTL – строго типизированный язык, однако контроль типовой правильности (корректности применения функций к их аргументам), который осуществляется в данной реализации динамически, то есть в процессе выполнения программы, увеличивает время ее выполнения на величину, составляющую до 30 % от времени выполнения программы. Заметим, что продвинутые механизмы контроля типов присутствуют в компиляторах и интерпретаторах многих функциональных языков, включая компилятор языка Haskell GHC [13]. В настоящей статье описана разработанная система статического (до выполнения программы) определения ее типовой корректности, что позволит существенно уменьшить время выполнения FPTL-программы. Язык FPTL Язык FPTL создавался как прообраз общепринятой в математической практике композиционной формы задания функций в общем случае в виде систем рекурсивных функциональных уравнений, в которой при построении новых функций используются операция подстановки функций вместо функциональных переменных и условный оператор. В FPTL введены четыре простые бинарные композиции функций, которые позволяют более тонко отражать композиционное представление функций и явно задают параллелизм при вычислении их значений. Функции в FPTL рассматриваются как типизированные (m, n)-арные соответствия (m≥0, n≥0) между кортежами данных, где m – длина кортежа на входе функции, n – на выходе. Функции арности (0, 1) рассматриваются в FPTL как константы. Для m и n, равных 0, имеем кортеж нулевой длины, обозначаемый λ, со свойствами λα=αλ=α, где α – произвольный кортеж. Кортеж данных в языке представляется в виде последовательной записи его элементов. В отличие от общепринятой формы задания функций с явным указанием ее аргументов (так называемая форма задания общего значения функции) в FPTL строго различаются собственно функция как отображение одного множества в другое, а также ее аппликация к конкретным данным. Роль переменных в задании функций в FPTL выполняют функции выбора необходимого элемента из кортежа данных. Формально функция выбора аргумента, обозначаемая I(i, m) (в языке – просто [i]), при применении к кортежу произвольного типа данных длины m (m>0) выбирает его i-й элемент, 0£i£m, m>0. Для i=0 выбираемое значение есть l. Функции в FPTL являются в общем случае частичными, причем неопределенное значение функции может быть выражено либо как неограниченный процесс вычисления ее значения, либо как специальное вычисляемое неопределенное значение, обозначаемое w, со свойствами wa=aw=a для любого кортежа a. Формально функции определяются как системы функциональных уравнений Fi=ti, i= Пусть f1, f2 – заданные функции, f – определяемая новая функция; a, b, g – обозначение кортежей. Синтаксис и семантика операций композиции определяются ниже. Сначала задается синтаксическая форма операции композиции, а затем ее семантическое значение; символ 1. Последовательная композиция (•): f (m, n)Û 2. Операция конкатенации кортежей значений функций (*):
3. Операция условной композиции:
4. Операция объединения (графиков) ортогональных функций:
Напомним, что ортогональными называются такие функции f1 и f2, что для всякого кортежа данных α определена не более, чем одна из них. Например, общепринятая форма условного оператора if p(x) then f1(x) else f2(x) в FPTL представляется как (p®f1)+( Все операции композиции обладают ассоциативностью, а операция объединения ортогональных функций является коммутативной. Приоритет операций композиции определяется следующим образом (в порядке возрастания): +, →, *, •. Введение приоритета операций позволяет опускать часть скобок в записи функций. При вычислении значений функций только операция последовательной композиции предполагает строгий порядок вычисления значений функций, к которым она применена. Остальные три операции композиции параллельны, причем для операций *, → допустим произвольный порядок вычисления значений функций, к которым она применена. Для операции + только одновременное (или квазипараллельное) вычисление значений функций гарантирует получение результата. Как уже было отмечено, термы в задании функций в виде системы функциональных уравнений Fi=ti, i= Определяемые абстрактные типы данных в FPTL задаются по аналогии с заданием функций в виде систем реляционных уравнений. В FPTL можно использовать встроенные типы bool, real, int, string и др. вместе с определенными в конкретной компьютерной системе операциями над ними. Для определения новых типов данных используются конструкторы и деструкторы (обратные конструкторам функции). Для определения типов данных применяются те же операции композиции, которые применяются для задания функций, за исключением того факта, что операция + трактуется как операция объединения двух множеств данных. Используемые в определении абстрактного типа данных (системе реляционных уравнений) конструкторы и деструкторы выполняют роль базисных функций. В проведенных ранее исследованиях [9] доказано, что их достаточно для того, чтобы в FPTL можно было представить любую вычислимую над абстрактными типами данных функцию. При определении абстрактных типов данных можно использовать встроенные типы данных. В языке также имеются конструкторы констант, позволяющие создавать данные встроенных типов. Приведем пример пользовательского типа. Определим тип «стек комплексных чисел»: data StackOfComplex{ Complex=real*real.c_complex; StackOfComplex=c_empty+(StackOfComplex*Complex).c_head; } В данном определении приводятся три конструктора: c_complex, c_empty и c_head, имеющие арности (2,1), (0,1) и (2,1) соответственно. В паре с определенными конструкторами определяются и деструкторы. Определения деструкторов извлекаются из определения типов и интерпретируются следующим образом:
В язык FPTL добавлена возможность задания параметризованных типов и функций. Приведем пример определения параметризованного стека, используя параметр ‘t (в FPTL обозначение типового параметра предваряется апострофом): data Stack[‘t]{ Stack=c_empty+(Stack[‘t]*‘t).c_head; } Приведем пример программы, вычисляющей количество элементов стека: data StackOfComplex{ Complex = real * real.c_complex; StackOfComplex=c_empty+(StackOfComplex* *Complex).c_head; } scheme Count { Count=~c_empty®0, ([1].~c_head.[2].Count * 1).add; } application stack=(((c_empty*((0.1*0.1).c_complex)).c_head)*((0.1* *0.1).c_complex)).c_head; %Count(stack); FPTL также поддерживает импорт функций из внешних модулей. Для импорта функции из другой функциональной программы или библиотеки используется конструкция: from «имя модуля» import «имя функции». Как уже отмечалось, язык FPTL имеет несколько реализаций и реализация FPTL на многоядерных компьютерах обладает рядом особенностей. Наиболее важной особенностью в контексте типового контроля является введение тернарной операции условной композиции взамен операций ® и +, которые главным образом предназначены для описания условных конструкций. Новая тернарная операция – аналог условного оператора if-then-else в традиционных языках программирования; она представляется в FPTL как (p®f1, f2), где p – предикат, f1 и f2 – функции, значение одной из которых будет использовано в зависимости от того, истинно или ложно значение p(x). Язык FPTL спроектирован так, что программирование на нем позволяет при помощи минимального набора средств, привычного для математической функциональной нотации, не прибегая к введению дополнительных и обычно нарушающих общую архитектуру языка примитивов, отражать и регулировать параллелизм в программе. Задание типов в FPTL Напомним, что в общем случае функции в FPTL задаются в виде систем рекурсивных функциональных уравнений: Fi=ti, i= Определение. Пусть T – множество константных типов, которое состоит из множества встроенных в FPTL типов (real, int, float, bool и др.) и абстрактных (определяемых пользователем в FPTL) типов; X – множество типовых переменных, таких, что каждая переменная xÎX принимает в качестве значений типы из T. Пусть далее Mk=M1´M2´…´Mk – множество кортежей длины k, построенных из элементов множества M=TÈX. Очевидно, что M0 состоит из единственного пустого кортежа, обозначаемого (как было указано выше) Кортеж типов длины k записывается следующим образом: z1´z2´…´zk, ziÎM, i= Кортеж типов, не содержащий переменные, называется константным. Кортеж типов, содержащий переменные, интерпретируется как множество константных кортежей, полученных путем всевозможных подстановок константных типов из Определение. Содержательно тип (m, n)-арной функции определяется как множество однозначных отображений {t1(i)´t2(i)´…´tm(i)®t1¢(i)´t2¢(i)´ …´tn¢(i), i=1, 2, …}, где справа и слева от символа ® стоят константные кортежи. Множество однозначных отображений может быть как конечным, так и счетным. Синтаксически тип функций задается в форме {z1(i)´z2(i)´…´zm(i)®z1¢(i)´z2¢(i)´…´zn¢(i), i=1, 2, …, k}. В интерпретации эта запись представляет множество константных отображений, полученных всевозможными подстановками константных типов в типовые кортежи слева и справа от символа ®. Предполагается, что одинаковым переменным, входящим в кортежи, присваиваются одни и те же типовые константы при подстановке. Требование однозначности в определении типа функции существенно, поскольку в случае его невыполнения мы получаем неопределенность. Проиллюстрируем это примером: пусть тип f (m, n) равен {int´int®real, int´int®int} Определение. Функция называется полиморфной, если входной либо выходной кортеж хотя бы одного из ее типовых элементов содержит типовую переменную или если тип функции содержит более одного типового элемента. Функция выбора i-го элемента из кортежа I(m, i) полиморфна и имеет тип {x1´x2´…´xi´… ´xm®xi}. Базисная функция сложения add полиморфна, поскольку ее тип состоит более чем из одного типового элемента: {int´int®int, int´real® ®real, real´int®real, real´real®real}. Условия правильной типизации функций в FPTL Пусть функции представлены в форме систем функциональных уравнений вида Fi=ti, i= Введем отношение порядка на множестве типов, положив t£t, xi£xj, t£x " tÎT, " x, xi, xjÎX. Отношение порядка на множестве кортежей вводится следующим образом: y1´y2´…´yk³z1´z2´…´zk, если yi³zi, i= Пусть a=y1´y2´…´ym®z1´z2´…´zn – типовой элемент. Тогда типовой кортеж y1´y2´…´ym называется входным и обозначается IN(a). Аналогично кортеж z1´z2´…´zn называется выходным и обозначается OUT(a). Для типа функции b={y1(i)´y2(i)´…´ym(i)®z1(i)´ ´z2(i)´…´zn(i), i=1, 2, …, k} определим IN(b) и OUT(b) как объединение множеств входных и выходных кортежей каждого типового элемента соответственно: IN(b)={IN(a)½aÎb}, OUT(b)= ={OUT(a)½aÎb}. Определим в введенных выше обозначениях условия корректной типизации для операций композиции. 1. t=t1×t2 – терм правильно типизирован, если IN(type(t2))³OUT(type(t1)); type(t1×t2)={(a®b)½aÎIN(type(t1))ÙbÎOUT(type(t2)) $b1 $b2 (b1£b2Ù(a®b1)Îtype(t1)Ù(b2®b)Îtype(t2)}. К условию правильной типизации для функций, полученных путем операции последовательной композиции, добавляется дополнительное условие, связанное с использованием функций выбора аргумента I(m, i), m>0, i³0. Как было указано, эти функции полиморфны и выполняют тождественное преобразование между данными на i-м входе и выходе функции. Для функции f, имеющей только константные типы, тип функции I(m, i)×f не является однозначным. Поэтому особым образом определяется тип функций I(m, i)×t: type(I(m, i)×t)={x1´x2´…´xm®OUT(t)½xiÎIN(t)}. 2. t=t1*t2 – терм правильно типизирован, если IN(type(t1))=IN(type(t2)); type(t1*t2)={(a®b)½aÎIN(type(t1))Ù$b1 $b2 (a®b1Îtype(t1)Ù(a®b2Îtype(t2))Ùb=b1´b2)}. 3. t=t1+t2 – терм правильно типизирован, если type(t1)=type(t2). 4. t1®t2 – терм правильно типизирован, если IN(type(t1))=IN(type(t2)); type(t1®t2)={(a®b)½(a®b)Î(type(t2))Ùa® ®boolÎtype(t1)}. Определим условия строгой правильной типизации функций, заданных в виде системы функциональных уравнений. Эти условия вытекают из правил типизации функций, полученных применением операций композиции функций, и необходимости равенства типов функциональных переменных Fi и термов ti, i= Добавим к условиям правильной типизации, определенным выше для операций композиции, еще два условия правильной типизации для функциональных уравнений: – типы термов ti и определяемых ими функциональных переменных Fi должны совпадать; – все вхождения функциональной переменной Fi в функциональные уравнения должны иметь одинаковый тип. Заметим, что функция может быть неправильно типизирована (в определенном выше смысле), однако при ее применении к данным конкретного типа она вычислит результат. Перейдем к рассмотрению алгоритма типового контроля в FPTL. Алгоритм типового контроля в FPTL По-прежнему исходим из общего задания функций в FPTL в форме системы функциональных уравнений Fi=ti, i= Перед проведением типового контроля производится ряд преобразований исходной системы функциональных уравнений. Сначала для каждой функциональной переменной Fi выполним для всех входящих в ti функциональных переменных подстановки tj вместо каждого вхождения Fj в ti. Cтроим
Повторяем процесс, строя Продолжаем этот процесс, пока для каждого Fi не будут получены Полученную систему функциональных уравнений Fi= Затем представим каждый терм A×(B+C)=(A×B)+(A×C), (A+B)×C=(A×C)+(B×C), A*(B+C)=(A*B)+(A*C), (A+B)*C=(A*C)+(B*C), A®(B+C)=(A®B)+(A®C), (A+B)®C=(A®C)+(B®C). Определение. Систему функциональных уравнений будем считать семантически корректной, если в представлении, полученном выше, в правой части для каждого терма Требование семантической корректности на практике не является сильно ограничивающим, поскольку программы, которые не обладают этим свойством, могут выполняться бесконечно, не приводя к получению результата. Очевидно, что в случае, если программа семантически корректна, процесс подстановки, описанный выше, не может длиться бесконечно. В дальнейшем будем рассматривать только семантически корректные системы функциональных уравнений. После построения приведенной системы функциональных уравнений для семантически корректной программы в каждом уравнении Fi=ti, i= Если это условие не выполняется, считается, что типизация не является правильной. Если оно выполняется в каждом уравнении приведенной системы уравнений, полагаем тип Fi, i= В реализации языка FPTL на многоядерных компьютерах вместо двух операций композиции функций Покажем работу алгоритма типового контроля на примере следующей программы:
Пусть type(f1)={int®int}, type(f2)={int®real}, type(f3)={int®int}, type(f4)={int®real}, type(f5)={real®int}, type(f6)={int®real}. Производим подстановку вместо F2 терма t2 в правой части уравнения F1=f1×F1+f2×F2+f3. Получаем В правой части уравнения F2=f4×F2×f5+F1×f6 нет терма, не содержащего функциональные переменные. Выполняем подстановки для F2: Проверяем выполнение условий типовой корректности для всех слагаемых в Пример можно изменить так, чтобы получить верную типизацию. Если все типы функций fi={int®int}, iÎ{1, 2, 3, 4, 5, 6}, то type(F1)= ={int®int}, type(F2)={int®int}. В заключение следует отметить, что по предварительным экспериментальным данным разработанные метод и алгоритм статического типового контроля правильности программы позволяют уменьшать до 30 % время выполнения программы на многоядерных компьютерах. Литература 1. McCarthy J. Recursive functions of symbolic expressions and their computation by machine. Cambridge, Mass.: MIT, 1960. 2. Milner R.G. The standard ML core language. Polymorphism. The ML/LCF/Hope Newsletter, 1985, vol. 2, no. 2. 3. Peyton Jones S.L. The implementation of functional programming languages. London: Prentice Hall, 1987. 4. Tim Harris, Simon Marlow, Simon Peyton Jones. Haskell on shared-memory multiprocessor. Proc. in Haskell workshop, 2005. 5. Church A. The calculi of lambda-conversion. Ann. of Math. Studies, Princeton, NJ, Princeton Univ. Press, 1941, vol. 6. 6. Клини С.К. Введение в метаматематику. М.: Иностранная литература, 1957. 7. Кутепов В.П. Исчисление функциональных схем и параллельные алгоритмы // Программирование. 1976. № 6. 8. Кутепов В.П., Фальк В.Н. Функциональные системы: теоретический и практический аспекты // Кибернетика. 1979. № 1. 9. Кутепов В.П., Фальк В.Н. Направленные отношения: теория и приложения // Изв. РАН: Техн. кибернетика. 1994. № 4, 5. 10. Бажанов C.Е., Кутепов В.П., Шестаков Д.А. Структурный анализ и планирование процессов параллельного выполнения функциональных программ // Изв. РАН. ТиСУ, 2005. № 6; Structural analysis and planning of processes of parallel execution of functional programs, Journ. of CSSI, 2005, vol. 44, no. 6. 11. Бажанов C.Е., Кутепов В.П., Шестаков Д.А. Язык функционального параллельного программирования и его реализация на кластерных системах // Программирование. 2005. № 5. 12. Кутепов В.П., Шамаль П.Н. Реализация языка функционального параллельного программирования FPTL на многоядерных вычислительных системах // Параллельные вычисления и задачи управления: сб. докл. VI Междунар. конф. М., 2012. 13. The Glasgow Haskell Compiler. URL: http://www.haskell. org/ghc (дата обращения: 14.02.2014). References 1. McCarthy J. Recursive functions of symbolic expressions and their computation by machine. Cambridge, Mass.: MIT Press, 1960. 2. Milner R.G. The standard ML core language. Polymorphism. The ML/LCF/Hope Newsletter. 1985, vol. 2, no. 2. 3. Peyton Jones S.L. The implementation of functional programming languages. London, Prentice Hall Publ., 1987. 4. Harris T., Marlow S., Jones S.P. Haskell on shared–memory multiprocessor. Proc. in Haskell workshop. 2005. 5. Church A. The calculi of lambda–conversion. Ann. of Math. Studies. Princeton, N.J., Princeton University Press, 1941, vol. 6. 6. Kleene S.C. Introduction to metamathematics. Amsterdam, Nord-Holland Publ. Co, 1952, 550 p. (Russ. ed.: Cleene C.K. Moscow, Inostrannaya literature Publ., 1957). 7. Kutepov V.P. Functional schemes computing and parallel algorithms. Programmirovanie [Programming]. 1976, no. 6. 8. Kutepov V.P., Falk V.N. Functional systems: theoretical and practical aspects. Kibernetika [Cubernetics]. 1979, no. 1. 9. Kutepov V.P., Falk V.N. Directed relations: theory and applications. Izv. RAN. Tekhn. kibernetika [Journ. of Computer and Systems Sciences International]. 1994, no. 4, 5. 10. Bazhanov C.E., Kutepov V.P., Shestakov D.A. Structural analysis and planning of processes of parallel execution of functional programs. Journ. of Computer and Systems Sciences International. 2005, vol. 44, no. 6, pp. 942–957. 11. Bazhanov C.E., Kutepov V.P., Shestakov D.A. Functional parallel programming language and its implementation on cluster systems. Programmirovanie [Programming]. 2005, no. 5, pp. 18–51. 12. Kutepov V.P, Shamal P.N. Multicore implementation of FPTL functional parallel programming language. Materialy konf. “Parallelnye vychisleniya i zadachi upravleniya” [Proc. VI Intern. Conf. “Parallel Computing and Control Problems”]. Moscow, 2012. 13. The Glasgow Haskell Compiler. Available at: http://www.haskell.org/ghc (accessed February 14, 2014). |
http://swsys.ru/index.php?id=3801&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Исследование эффективности библиотеки MaLLBa на примере задач максимальной выполнимости
- Параллельные вычисления при моделировании процесса растворения на микроуровне
- Построение адаптивной регулярной сетки трехмерной сцены в реальном режиме времени
- Неоднозначная семантика и некорректности при работе с потоками на C#
- Моделирование столкновения двух атомов над поверхностью конденсированной фазы

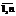 , где ti – функциональные термы, построенные из заданных (базисных) функций и функциональных переменных Fi путем применения четырех операций композиции функций: →, +, *, •. Для функций и функциональных переменных задана их арность, а для базисных функций еще и их тип.
, где ti – функциональные термы, построенные из заданных (базисных) функций и функциональных переменных Fi путем применения четырех операций композиции функций: →, +, *, •. Для функций и функциональных переменных задана их арность, а для базисных функций еще и их тип. обозначает равенство по определению.
обозначает равенство по определению. ; f(a)Ûf2(f1(a)).
; f(a)Ûf2(f1(a)). ; f(a)Ûf1(a)f2(a).
; f(a)Ûf1(a)f2(a). ;
;
 ;
;
 ®f2). Операция объединения ортогональных функций была введена с целью представления параллельных функций (известный пример – функция голосования в телефонии).
®f2). Операция объединения ортогональных функций была введена с целью представления параллельных функций (известный пример – функция голосования в телефонии). , представляют собой функциональные выражения, построенные из базисных функций и функциональных переменных путем применения операций композиции. Предполагается, что арности терма и определяемой им функциональной переменной в системе функциональных уравнений одинаковы. Функциональные переменные выполняют двойную роль при задании функции (построении функциональной программы): одни из них появляются как необходимые элементы при задании рекурсивных функций, другие определяются далее (в следующем уравнении уточняемой функции). Это позволяет просто реализовать пошаговую разработку функциональной программы по технологии проектирования «сверху–вниз», уточняя введенную функциональную переменную, определяя ее в следующем функциональном уравнении.
, представляют собой функциональные выражения, построенные из базисных функций и функциональных переменных путем применения операций композиции. Предполагается, что арности терма и определяемой им функциональной переменной в системе функциональных уравнений одинаковы. Функциональные переменные выполняют двойную роль при задании функции (построении функциональной программы): одни из них появляются как необходимые элементы при задании рекурсивных функций, другие определяются далее (в следующем уравнении уточняемой функции). Это позволяет просто реализовать пошаговую разработку функциональной программы по технологии проектирования «сверху–вниз», уточняя введенную функциональную переменную, определяя ее в следующем функциональном уравнении.


 .
. .
. вместо вхождения в кортеж переменных типов.
вместо вхождения в кортеж переменных типов. Представим ситуацию, когда на входе f имеется кортеж из двух целых чисел. Понятно, что мы не можем однозначно определить выходной типовой кортеж, поскольку неочевидно, какое число – целое или вещественное – нам ожидать на выходе. Однозначность не выполняется для функций, имеющих типы {x®y} и {x®t}, tÎT; x, yÎX.
Представим ситуацию, когда на входе f имеется кортеж из двух целых чисел. Понятно, что мы не можем однозначно определить выходной типовой кортеж, поскольку неочевидно, какое число – целое или вещественное – нам ожидать на выходе. Однозначность не выполняется для функций, имеющих типы {x®y} и {x®t}, tÎT; x, yÎX. Будем исходить из предположения, что типы всех входящих в правые части ti
Будем исходить из предположения, что типы всех входящих в правые части ti  базисных функций (встроенных функций, функций-конструкторов и деструкторов в определении абстрактных типов данных) заданы.
базисных функций (встроенных функций, функций-конструкторов и деструкторов в определении абстрактных типов данных) заданы. меньше или равен типу функции
меньше или равен типу функции  (type(f1)£type(f2)), если выполнено условие: для каждого типового элемента
(type(f1)£type(f2)), если выполнено условие: для каждого типового элемента 
 , принадлежащего type(f1), существует типовой элемент
, принадлежащего type(f1), существует типовой элемент 
 , принадлежащий type(f2), такой, что
, принадлежащий type(f2), такой, что 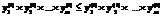 и
и 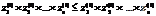 . Положим, что type(f1)=type(f2)Ûtype(f1)£type(f2)Ùtype(f1)³ ³type(f2).
. Положим, что type(f1)=type(f2)Ûtype(f1)£type(f2)Ùtype(f1)³ ³type(f2). i=
i= путем подстановок вместо всех новых функциональных переменных, входящих в
путем подстановок вместо всех новых функциональных переменных, входящих в  (переменных, которые появились в
(переменных, которые появились в  такие, что в
такие, что в  не существует вхождений функциональных переменных, для которых ранее не выполнялась подстановка.
не существует вхождений функциональных переменных, для которых ранее не выполнялась подстановка. , где термы
, где термы  не содержат вхождений операции
не содержат вхождений операции  . Для этого используются следующие правила эквивалентности:
. Для этого используются следующие правила эквивалентности: имеется хотя бы один терм tj, не содержащий функциональные переменные. Если в процессе построения приведенной системы уравнений получилось более одного слагаемого, не содержащего функциональные переменные, проверяем выполнение условий правильной типизации для операции +, то есть равенство типов слагаемых.
имеется хотя бы один терм tj, не содержащий функциональные переменные. Если в процессе построения приведенной системы уравнений получилось более одного слагаемого, не содержащего функциональные переменные, проверяем выполнение условий правильной типизации для операции +, то есть равенство типов слагаемых. в соответствующее слагаемое
в соответствующее слагаемое  , считаем, что типизация рассматриваемой системы функциональных уравнений правильна. В противном случае считается, что правильность типизации нарушена.
, считаем, что типизация рассматриваемой системы функциональных уравнений правильна. В противном случае считается, что правильность типизации нарушена. и + используется более эффективная с точки зрения параллельного выполнения программ тернарная операция, эквивалентная условному оператору в последовательных языках программирования. Эта операция записывается в форме t1®t2, t3, где t1 – терм-условие. Легко показать, что она эквивалентна представлению (t1®t2)+(
и + используется более эффективная с точки зрения параллельного выполнения программ тернарная операция, эквивалентная условному оператору в последовательных языках программирования. Эта операция записывается в форме t1®t2, t3, где t1 – терм-условие. Легко показать, что она эквивалентна представлению (t1®t2)+( ®t3). Поэтому перед применением алгоритма контроля типовой правильности функциональной программы все вхождения в нее термов, полученных путем применения тернарной операции, приводятся к данной эквивалентной форме.
®t3). Поэтому перед применением алгоритма контроля типовой правильности функциональной программы все вхождения в нее термов, полученных путем применения тернарной операции, приводятся к данной эквивалентной форме.
 =f1×F1+f2×(f4×F2×f5+F1×f6)+f3=f1×F1+f2×f4×F2×f5+ +f2×F1×f6+f3. Все подстановки для F1 сделаны, заметим, что в
=f1×F1+f2×(f4×F2×f5+F1×f6)+f3=f1×F1+f2×f4×F2×f5+ +f2×F1×f6+f3. Все подстановки для F1 сделаны, заметим, что в  =f4×F2×f5+ +(f1×F1+f2×F2+f3)×f6=f4×F2×f5+f1×F1×f6+f2×F2×f6+f3×f6. В результате подстановки появился терм f3×f6, не содержащий функциональные переменные. В соответствии с правилами определения типов для операции композиции получаем, что type(f3×f6)= ={int®real}. Из этого следует, что тип функции F2 равен {int®real}.
=f4×F2×f5+ +(f1×F1+f2×F2+f3)×f6=f4×F2×f5+f1×F1×f6+f2×F2×f6+f3×f6. В результате подстановки появился терм f3×f6, не содержащий функциональные переменные. В соответствии с правилами определения типов для операции композиции получаем, что type(f3×f6)= ={int®real}. Из этого следует, что тип функции F2 равен {int®real}. содержащих вхождения функциональных переменных, считая их тип определенным ранее: type(f1×F1)={int®int}. При проверке типовой корректности выражения f2×f4×F2×f5 встречаем ошибку типизации – тип функции f2 равен {int®real}, как и тип функции f4 равен {int®real}. Делаем вывод о неверной типизации.
содержащих вхождения функциональных переменных, считая их тип определенным ранее: type(f1×F1)={int®int}. При проверке типовой корректности выражения f2×f4×F2×f5 встречаем ошибку типизации – тип функции f2 равен {int®real}, как и тип функции f4 равен {int®real}. Делаем вывод о неверной типизации.