В данной работе в качестве объекта управления (ОУ) выступают манипуляторы с избыточным числом степеней свободы. Избыточные манипуляторы имеют большее число степеней свободы, чем это необходимо для выполнения задачи, то есть большее, чем размерность рабочего пространства.
Избыточность степеней свободы позволяет структуре манипулятора адаптироваться в условиях недостаточной информации о внешней (возможно, изменяющейся) среде в условиях изме- нения свойств самого манипулятора (например, связанных со старением или выходом из строя отдельных узлов). Кроме того, избыточные степени свободы позволяют задать поведение робота-манипулятора при решении поставленной задачи с минимальным расходом полезного ресурса.
В настоящее время производятся промышленные роботы для манипулирования, сварки, покраски, упаковки, шлифовки, полировки и прочего с большим спектром применения и по точности, и по характеру выполняемых операций. Основными массовыми потребителями в области промышленной робототехники являются автомобильная и электронная промышленность.
Задачи управления для избыточных роботов-манипуляторов (позиционирование устройства захвата, построение траектории, решение обратной задачи динамики и др.) с увеличением сложности ОУ, повышением требований к работоспособности в критических ситуациях и в условиях неблагоприятной внешней среды все чаще решаются с применением технологий интеллектуальных вычислений: генетических алгоритмов (ГА) [1, 2], нейронных и нечетких нейронных сетей [3, 4], с использованием аппарата нечеткой логики [5, 6].
В данной работе рассматривается применение технологий мягких вычислений [7] для построения робастной интеллектуальной системы управления для решения задачи позиционирования избыточного робота-манипулятора с семью степенями свободы.
Построение системы управления манипулятором с семью степенями свободы с постоянными параметрами регулятора
Традиционная система управления состоит из звена регулирования, ОУ и измерительной системы (ИС) в цепи обратной связи. Среди различных типов регуляторов широко распространены пропорционально-интегрально-дифференциальные (ПИД) регуляторы.
В общем случае необходимо найти коэффициенты ПИД-регулятора KПi, KДi, KИi, 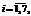 при которых обеспечивается желаемый характер движения звеньев робота-манипулятора.
при которых обеспечивается желаемый характер движения звеньев робота-манипулятора.
Для определения коэффициентов KПi, KДi, KИi, 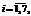 аналитическими методами необходимы первоначальные знания о системе управления и характере поведения ОУ [8, 9], то есть корректное определение коэффициентов ПИД-регулятора возможно с привлечением эксперта.
аналитическими методами необходимы первоначальные знания о системе управления и характере поведения ОУ [8, 9], то есть корректное определение коэффициентов ПИД-регулятора возможно с привлечением эксперта.
Включение в систему управления элементов интеллектуальных вычислений позволяет описывать требования к системе управления в терминах качественных критериев.
Так, определение параметров управления возможно с использованием ГА, для чего необходимо лишь корректно определить функцию пригодности (fitness-функцию) ГА, например, следующим образом: fitness=(PTS=1)Ç(IT®0), где PTS (Position Task Solution) – решение задачи позиционирования манипулятором с тремя степенями свободы, а IT – быстродействие системы управления, то есть выбор коэффициентов KПi, KДi, KИi, 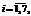 определяется исходя из обеспечения гарантированного решения задачи позиционирования с максимальным быстродействием. Интеллектуальная надстройка в виде звена ГА без разрушения нижнего исполнительного уровня позволяет оперировать качественными критериями системы.
определяется исходя из обеспечения гарантированного решения задачи позиционирования с максимальным быстродействием. Интеллектуальная надстройка в виде звена ГА без разрушения нижнего исполнительного уровня позволяет оперировать качественными критериями системы.
Выбор коэффициентов ПИД-регулятора в системе управления на основе ГА осуществляется один раз для одного или ряда случаев (штатные ситуации управления), в процессе работы коэффициенты остаются неизменными. В результате система управления на основе ГА справляется с задачей точного позиционирования манипулятора в штатных ситуациях, но не обеспечивает гарантированное управление в непредвиденных ситуациях.
Применение системы управления на основе ГА ограничено требованием наличия описания постоянных условий внешней среды и известных структур управляющего звена и ОУ.
Расширение применимости системы управления возможно с помощью увеличения интеллектуальности системы управления – использования динамической настройки коэффициентов ПИД-регулятора, что возможно с включением элементов технологии мягких вычислений.
Проектирование интеллектуальной системы управления с применением технологий мягких вычислений
Основным элементом интеллектуальной системы управления (ИСУ) с применением технологий мягких вычислений [7] является нечеткий регулятор (НР), управляющий коэффициентами усиления ПИД-регулятора. НР осуществляет управление за счет интегрированной в него базы знаний (БЗ), включающей данные о виде и параметрах функций принадлежности входных и выходных нечетких переменных, а также набор нечетких продукционных правил.
БЗ создается с помощью интеллектуального инструментария – оптимизатора БЗ (ОБЗ) на основе мягких вычислений.
Разработка БЗ рассмотрена ранее на примере робота-манипулятора с тремя степенями свободы [10]. Было показано, что в зависимости от сложности системы и ОУ ИСУ на ОБЗ на мягких вычислениях может содержать один или несколько НР. С увеличением сложности ОУ увеличивается время создания БЗ, повышаются требования к вычислительным ресурсам процессора, на котором создается БЗ, и к объему памяти системы, в которой размещается БЗ.
Когда сложность реализации единой БЗ высока, создаются несколько БЗ, которые размещаются в разных НР. Разделение управления несколько снижает качество системы, однако создание нескольких НР нередко является единственным способом организации интеллектуального управления сложным ОУ, таким как робот-манипулятор с семью степенями свободы.
В связи со сложностью рассматриваемого объекта управления реализация единой БЗ невозможна, поэтому изначально организуем разделенное управление звеньями (один НР управляет одним звеном, как показано на рис. 1).
Формирование БЗ происходит в следующей последовательности:
– создание обучающего сигнала – определение типовой ситуации управления (например штатная ситуация), формирование таблицы коэффициентов ПИД-регулятора и ошибок управления с помощью ГА;
– формирование модели нечеткого вывода – определение типа нечеткой модели, интерпретации нечетких операций, числа входных и выходных переменных;
– создание лингвистических переменных для входных значений;
– создание и настройка базы правил;
– оптимизация левых и правых частей пра- вил БЗ.
Для исследования качества рассмотренных систем управления в среде MatLab/Simulink было проведено моделирование систем управления манипулятором с семью степенями свободы.
Порядок проведения и оценка экспериментов
В предположении, что звенья робота-манипулятора могут вращаться в диапазоне ±70 градусов и конфигурации степеней свободы соответ- ствуют представлению на рисунке 1, была построена формализованная модель манипулятора с семью степенями свободы, что позволило ускорить идентификацию модели ОУ, а также получение приемлемых параметров управления для разных типов систем управления и с различным уровнем интеллектуальности.
Для MatLab/Simulink-моделей проведена серия экспериментов, включающая два этапа: работа в штатных и работа в непредвиденных (нештатных) ситуациях управления.
В качестве штатных ситуаций управления выступают тринадцать экспериментов в соответствии с группой точек рабочего пространства, определенных как тестовые.
Нештатные ситуации разделяются на внешние (принудительное изменение положения звеньев, изменение начальных условий или одновременно и принудительное изменение положений звеньев, и изменение начальных условий) и внутренние (уменьшение или увеличение ограничений управляющих воздействий, внесение шумов в каналы управления или в систему измерения). Каждая из непредвиденных ситуаций тестируется на тринадцати точках тестового пространства; таким образом, проводятся 39 экспериментов для внешних и 52 эксперимента для внутренних непредвиденных ситуаций управления.
Для оценки и сравнения результатов испытаний введена система критериев качества, учитывающая методы оценки переходных процессов теории автоматического управления [9]. Данные методы были адаптированы для конкретного ОУ (робота-манипулятора с семью степенями свободы) в следующем виде.
1. Решение задачи позиционирования в штатных ситуациях управления PTSKCS (Position Task Solution in known control situations). Задача позиционирования считается решенной, если по завершении заданного числа итераций Imax=300 выполняется условие

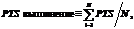
![Подпись: Рис. 1. ИСУ роботом-манипулятором с семью степенями свободы на оптимизаторе БЗ на мягких вычислениях:Qref – воздействующий (задающий) сигнал; Q¢ – измеренная регулируемая величина; s(t) – ограничение управляющего воздействия; d(t) – задержка в ИС; m(t) – внешнее воздействие среды; E=[e1 e2 … e7] – ошибка управления; U=[u1 u2 … u7] – управляющее воздействие; TSi, – обучающий сигнал соответствующего НР; Q=[q1 q2 … q7] – регулируемая величина [11]Fig. 1. ICS for 7-degrees-of-freedom robot manipulator based on Soft Computing Optimizer (SCO):Qref – reference signal; Q’ – measured controlled variable; s(t) – control signal saturation; d(t) – delay in measured system; m(t) – impact of the environment; E=[e1 e2 … e7] – operating error; U=[u1 u2 … u7] – control signal; TSi, – teaching signal of relevant fuzzy controller; Q=[q1 q2 … q7] – controlled variable [11]](phpThumb/phpThumb.php?w=300&src=/uploaded/image/2014-2/image188.gif) где q1ref, q2ref, …, q7ref – желаемые положения звеньев; q1, q2, …, q7 – текущие положения звеньев; N – число экспериментов.
где q1ref, q2ref, …, q7ref – желаемые положения звеньев; q1, q2, …, q7 – текущие положения звеньев; N – число экспериментов.
2. Решение задачи позиционирования во внешних непредвиденных ситуациях управления PTSACCS1 (Position Task Solution in the above considered control situations).
3. Решение задачи позиционирования во внутренних непредвиденных ситуациях управления PTSACCS2.
4. Быстродействие IT. Количество итераций от начала воздействия, в течение которых осуществляется позиционирование каждого из звеньев с допустимой ошибкой 2D<1deg:
 ,
, 
5. Относительное значение перерегулирования σ. Отношение максимального отклонения текущего положения звена от установившегося значения к установившемуся значению:

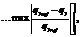

6. Относительная ошибка позиционирования звеньев по завершении заданного числа итера- ций ε:

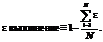
7. Время одной итерации t. Реальное время выполнения одной итерации I выбранного типа системы управления: 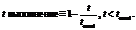
8. Сложность реализации управления P. Оценка изменения коэффициентов управления:

9. Общая оценка управления FCB (Full Control Behavior):

где w=[0,1 0,2 0,2 0,2 0,05 0,1 0,1 0,05] – весовые коэффициенты.
Качество систем управления с постоянными коэффициентами ПИД-регулятора
Как уже было отмечено, задача управления сводится к нахождению коэффициентов ПИД-регулятора, при которых обеспечивается желаемый характер движения манипулятора. Рассматри- ваются два типа систем автоматического управления (САУ) с постоянными коэффициентами: система управления на ПИД-регуляторе и с использованием ГА. Сравнение работы систем управления манипулятором с семью степенями свободы на основе ПИД-регулятора и с использованием ГА в соответствии с введенной системой критериев качества приведено в таблице.
Сравнение работы систем управления с постоянными коэффициентами
Work comparison of control systems with constant coefficients
|
Критерий качества
|
Качество управления
|
САУ
|
|
на основе ПИД-регулятора
|
с использованием ГА
|
|
1
|
Решение в штатных ситуациях управления
|
0,000
|
0,615
|
|
2
|
Решение в непредвиденных ситуациях: внешние возмущающие воздействия
|
0,000
|
0,256
|
|
3
|
Решение в непредвиденных ситуациях: изменения параметров ОУ
|
0,058
|
0,308
|
|
4
|
Быстродействие
|
0,000
|
0,008
|
|
5
|
Относительное значение перерегулирования
|
0,892
|
0,956
|
|
6
|
Относительная ошибка позиционирования звеньев
|
0,379
|
0,657
|
|
7
|
Время одной итерации
|
0,998
|
0,998
|
|
8
|
Сложность реализации управления
|
1,000
|
1,000
|
|
9
|
Общее управление
|
0,244
|
0,439
|
Из результатов сравнения двух типов систем управления (на основе ПИД-регулятора и с использованием ГА) делаем следующие выводы:
– при использовании САУ на ПИД-регу- ляторе задача позиционирования не решена ни в одном эксперименте в штатных ситуациях и внешних непредвиденных ситуациях управле- ния; незначительные положительные результаты (3 эксперимента из 52) получены для внутренних непредвиденных ситуаций управления;
– некоторое улучшение достигается при использовании САУ на основе ГА: решение задачи позиционирования в штатных ситуациях управления достигается в большинстве экспериментов, однако в непредвиденных ситуациях управления (как внешних, так и внутренних) решение достигнуто менее чем в трети экспериментов;
– при использовании САУ на ГА значительно улучшаются показатели относительных значений перерегулирования и ошибок позиционирования по сравнению с системой управления на ПИД-регуляторе;
– при использовании САУ на ГА общая оценка управления по сравнению с системой управления на ПИД-регуляторе улучшается в 1,8 раза;
– системы управления с постоянными коэффициентами имеют низкое быстродействие.
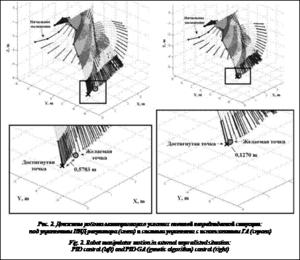 На рисунке 2 продемонстрирована работа манипулятора при использовании систем управления на ПИД-регуляторе и с использованием ГА в условиях третьей внешней непредвиденной ситуации управления (изменено начальное положение, и в разные моменты времени звенья принудительно перемещаются). В выбранном для демонстрации эксперименте система управления на ГА решает задачу управления в отличие от системы управления на ПИД-регуляторе.
На рисунке 2 продемонстрирована работа манипулятора при использовании систем управления на ПИД-регуляторе и с использованием ГА в условиях третьей внешней непредвиденной ситуации управления (изменено начальное положение, и в разные моменты времени звенья принудительно перемещаются). В выбранном для демонстрации эксперименте система управления на ГА решает задачу управления в отличие от системы управления на ПИД-регуляторе.
Система управления на ГА значительно улучшает оценки критериев качества по сравнению с системой управления на ПИД-регуляторе, однако в целом качество управления, обеспечиваемое системой управления на ГА, довольно низкое.
В процессе управления коэффициенты ПИД-регулятора для рассмотренных структур не изменяются. Данное обстоятельство, с одной стороны, облегчает проектирование системы управления, а с другой – лишает систему управления возможности перестроения и адаптации.
Поэтому в качестве следующей ступени развития систем управления рассмотрим структуру с динамической адаптацией коэффициентов ПИД-регулятора, реализованной на основе технологий мягких вычислений.
Качество систем управления с применением технологий мягких вычислений
Тестирование полученных БЗ1−БЗ7 соответственно НР1−НР7 проводится в составе ИСУ на ОБЗ на мягких вычислениях. Результаты испытаний ИСУ на ОБЗ на мягких вычислениях в соответствии с введенной системой критериев качества в сравнении с системами управления с постоянными коэффициентами (на основе ПИД-регулятора и с использованием ГА) приведены на рисунке 3.
Результаты сравнения систем управления (ИСУ на ОБЗ на мягких вычислениях, системы управления на основе ПИД-регулятора и с использованием ГА) показали, что при использовании ИСУ на ОБЗ на мягких вычислениях
– повысился процент решения задачи позиционирования в штатных ситуациях (решение положительное в 12 из 13 экспериментов) по сравнению с системами управления с постоянными коэффициентами (см. (1) на рис. 3);
– 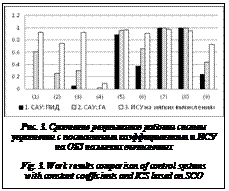 значительно повысился процент решения задачи позиционирования в непредвиденных ситуациях управления по сравнению с системами управления с постоянными коэффициентами: для внешних непредвиденных ситуаций ((2) на рис. 3) в 2,9 раза и в 3 раза для внутренних непредвиденных ситуаций ((3) на рис. 3) в сравнении с системой управления на основе ГА;
значительно повысился процент решения задачи позиционирования в непредвиденных ситуациях управления по сравнению с системами управления с постоянными коэффициентами: для внешних непредвиденных ситуаций ((2) на рис. 3) в 2,9 раза и в 3 раза для внутренних непредвиденных ситуаций ((3) на рис. 3) в сравнении с системой управления на основе ГА;
– улучшились показатели относительного значения перерегулирования и относительной ошибки позиционирования звеньев ((5) и (6) на рис. 3) по сравнению с системами управления с постоянными коэффициентами, но немного ухудшились оценки времени одной итерации и сложности реализации управления ((7) и (8) на рис. 3);
– улучшилась общая оценка управления по сравнению с САУ на основе ГА в 1,7 раза, а с САУ на ПИД-регуляторе – в 3 раза ((9) на рис. 3);
– значительно увеличилось быстродействие: более чем в 10 раз по сравнению с САУ на основе ГА; однако по-прежнему быстродействие достаточно низкое ((4) на рис. 3).
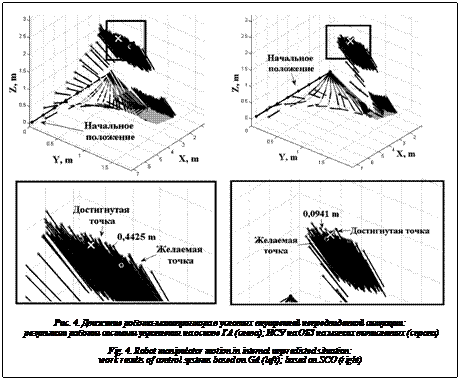 На рисунке 4 продемонстрирована работа манипулятора при использовании системы управления на основе ГА и ИСУ на ОБЗ на мягких вычислениях в условиях четвертой внутренней непредвиденной ситуации управления (внесение погрешностей в систему измерения).
На рисунке 4 продемонстрирована работа манипулятора при использовании системы управления на основе ГА и ИСУ на ОБЗ на мягких вычислениях в условиях четвертой внутренней непредвиденной ситуации управления (внесение погрешностей в систему измерения).
ИСУ роботом-манипулятором с семью степенями свободы на ОБЗ на мягких вычислениях значительно улучшает качество управления по сравнению с системами управления с постоянными коэффициентами (на основе ПИД-регулятора и с использованием ГА), однако показатель быстродействия остается на достаточно низком уровне.
Ввиду того, что ОУ сложен, ИСУ на ОБЗ на мягких вычислениях была организована с разделением управления: каждому звену манипулятора соответствует один независимый НР. Однако декомпозиция управления ведет к рассогласованию работы и к некоторому снижению качества управления.
Организовать координационное управление без значительного увеличения сложности системы возможно путем введения дополнительных обобщающих звеньев, реализуемых с использованием технологий квантовых вычислений.
В заключение необходимо отметить, что на примере сложного ОУ (робота-манипулятора с семью степенями свободы) были рассмотрены принципы проектирования систем управления: классических – на основе ПИД-регулятора и с применением ГА, а также с использованием технологий мягких вычислений.
На уровне моделирования (с использованием пакета MatLab/Simulink) продемонстрировано следующее: система управления с постоянными коэффициентами на основе ПИД-регулятора при управлении сложным ОУ не способна решить задачу точного позиционирования даже в штатных ситуациях управления; система управления с постоянными коэффициентами с использованием ГА решает задачу точного позиционирования в штатных ситуациях управления, однако плохо справляется с этим в условиях непредвиденных си- туаций управления; ИСУ на ОБЗ на мягких вычислениях в большинстве случаев справляется с решением задачи позиционирования как в штатных, так и в непредвиденных ситуациях управления в отличие от систем управления с постоянными коэффициентами, при этом она улучшает оценки по основным показателям критериев качества.
Литература
1. Khoogar A.R., Parker J.K. Obstacle Avoidance for Redundant Manipulators Using a Genetic Algorithm. Southeastcon´91 Conf., Williamsburg, VA, 7−10 Apr., 1991, vol. 1, pp. 317–320.
2. Secara C., Vladareanu L. Iterative genetic algorithm based strategy for obstacles avoidance of a redundant manipulator. Wseas Transaction on Mathematics. 2010, vol. 9, no. 3, pp. 211–221.
3. Yu W., Rosen J. Neural PID Control of Robot Manipulators With Application to an Upper Limb Exoskeleton. Cybernetics, IEEE Transactions, 2013, vol. 43, no. 2, pp. 673–684.
4. Jasour A.M., Farrokhi M. Path Tracking and Obstacle Avoidance for Redundant Robotic Arms Using Fuzzy NMPC. American Control Conf., Hyatt Regency Riverfront, St. Louis, MO, USA, 10−12 June, 2009, pp. 1353–1358.
5. Meza J.L., Santibanez V., Soto R., Liama M.A. Fuzzy Self-Tuning PID Semiglobal Regulator for Robot Manipulators. Industrial Electronics, IEEE Transactions. 2012, vol. 59, no. 6, pp. 2709–2717.
6. Salas F.G., Santibanez V., Llama M.A. Variable Gains PD Tracking Control of Robot Manipulators: Stability Analysis and Simulations. World Automation Congress (WAC), Puerto Vallarta, Mexico, 24−28 June, 2012, pp. 1–6.
7. Ульянов С.В., Литвинцева Л.В., Добрынин В.Н., Мишин А.А. Интеллектуальное робастное управление: технологии мягких вычислений. М.: Изд-во ВНИИгеосистем, 2011. 408 c.
8. Panda R.C. Introduction to PID Controllers − Theory, Tuning and Application to Frontier. Rijeka, Croatia: InTech, 2012, 258 p.
9. Михайлов В.С. Теория управления. К.: Выща школа, 1988. 312 c.
10. Николаева А.В., Ульянов С.В. Интеллектуальное управление роботом-манипулятором на основе мягких вы- числений // Программные продукты и системы. 2013. № 4. С. 150–155.
11. Филлипс Ч., Харбор Р. Системы управления с обратной связью. M.: Лаборатория базовых знаний, 2001. 616 c.
References
1. Khoogar A.R., Parker J.K. Obstacle avoidance for redundant manipulators using a genetic algorithm. Southeastcon´91 conf. Williamsburg, VA, 1991, vol. 1, pp. 317–320.
2. Secara C., Vladareanu L. Iterative genetic algorithm based strategy for obstacles avoidance of a redundant manipulator. Wseas Transaction on Mathematics. 2010, vol. 9, no. 3, pp. 211–221.
3. Yu W., Rosen J. Neural PID control of robot manipulators with application to an upper limb exoskeleton. Cybernetics, IEEE Transactions. 2013, vol. 43, no. 2, pp. 673–684.
4. Jasour A.M., Farrokhi M. Path tracking and obstacle avoidance for redundant robotic arms using fuzzy NMPC. American control conf. Hyatt Regency Riverfront, St. Louis, MO, USA, 2009, pp. 1353–1358.
5. Meza J.L., Santibanez V., Soto R., Liama M.A. Fuzzy self-tuning PID semiglobal regulator for robot manipulators. In- dustrial Electronics, IEEE Transactions. 2012, vol. 59, no. 6, pp. 2709–2717.
6. Salas F.G., Santibanez V., Llama M.A. Variable gains PD tracking control of robot manipulators: stability analysis and simulations. Proc. of World Automation Congress (WAC). Puerto Vallarta, Mexico, 2012, pp. 1–6.
7. Ulyanov S.V., Litvintseva L.V., Dobrynin V.N., Mi- shin A.A. Intellektualnoe robastnoe upravlenie: tekhnologii myagkikh vychisleniy [Intelligent robust control: soft computing technologies]. Moscow, VNIIgeosistem Publ., 2011, 408 p.
8. Panda R.C. Introduction to PID Controllers − theory, tuning and application to frontier areas. Rijeka, Croatia, InTech Publ., 2012, 258 p.
9. Mikhaylov V.S. Teoriya upravleniya [Control theory]. Kiev, Vyshcha shkola Publ., 1988, 312 p.
10. Nikolaeva A.V., Ulyanov S.V. Intelligent control of a robot manipulator based on soft computing. Programmnye produkty i sistemy [Software & Systems]. 2013, no. 4, pp. 150–155.
11. Phillips Ch., Harbor R. Feedback control systems. Prentice Hall Publ., 1991, 664 p.

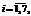 при которых обеспечивается желаемый характер движения звеньев робота-манипулятора.
при которых обеспечивается желаемый характер движения звеньев робота-манипулятора.
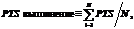
![Подпись: Рис. 1. ИСУ роботом-манипулятором с семью степенями свободы на оптимизаторе БЗ на мягких вычислениях:Qref – воздействующий (задающий) сигнал; Q¢ – измеренная регулируемая величина; s(t) – ограничение управляющего воздействия; d(t) – задержка в ИС; m(t) – внешнее воздействие среды; E=[e1 e2 … e7] – ошибка управления; U=[u1 u2 … u7] – управляющее воздействие; TSi, – обучающий сигнал соответствующего НР; Q=[q1 q2 … q7] – регулируемая величина [11]Fig. 1. ICS for 7-degrees-of-freedom robot manipulator based on Soft Computing Optimizer (SCO):Qref – reference signal; Q’ – measured controlled variable; s(t) – control signal saturation; d(t) – delay in measured system; m(t) – impact of the environment; E=[e1 e2 … e7] – operating error; U=[u1 u2 … u7] – control signal; TSi, – teaching signal of relevant fuzzy controller; Q=[q1 q2 … q7] – controlled variable [11]](phpThumb/phpThumb.php?w=300&src=/uploaded/image/2014-2/image188.gif)
 ,
, 

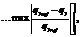


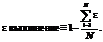
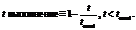



 значительно повысился процент решения задачи позиционирования в непредвиденных ситуациях управления по сравнению с системами управления с постоянными коэффициентами: для внешних непредвиденных ситуаций ((2) на рис. 3) в 2,9 раза и в 3 раза для внутренних непредвиденных ситуаций ((3) на рис. 3) в сравнении с системой управления на основе ГА;
значительно повысился процент решения задачи позиционирования в непредвиденных ситуациях управления по сравнению с системами управления с постоянными коэффициентами: для внешних непредвиденных ситуаций ((2) на рис. 3) в 2,9 раза и в 3 раза для внутренних непредвиденных ситуаций ((3) на рис. 3) в сравнении с системой управления на основе ГА; На рисунке 4 продемонстрирована работа манипулятора при использовании системы управления на основе ГА и ИСУ на ОБЗ на мягких вычислениях в условиях четвертой внутренней непредвиденной ситуации управления (внесение погрешностей в систему измерения).
На рисунке 4 продемонстрирована работа манипулятора при использовании системы управления на основе ГА и ИСУ на ОБЗ на мягких вычислениях в условиях четвертой внутренней непредвиденной ситуации управления (внесение погрешностей в систему измерения).