В данной работе в качестве объекта управления (ОУ) выступают манипуляторы с избыточным числом степеней свободы. Избыточность степеней свободы позволяет манипулятору адаптироваться в условиях недостаточной информации о внешней среде при изменении параметров самого ОУ.
Авторами уже были рассмотрены системы управления с постоянными и динамически изменяющимися коэффициентами (на основе технологий мягких вычислений) роботом-манипулятором с семью степенями свободы (см. с. 49–55 настоящего номера журнала).
Было продемонстрировано, что при использовании системы управления на основе пропорционально-интегрально-дифференциального (ПИД) регулятора в штатных ситуациях и во внешних непредвиденных ситуациях управления задача позиционирования не была решена, незначительные положительные результаты были получены только для внутренних непредвиденных ситуаций управления. Некоторое улучшение наблюдалось при использовании системы управления на основе генетического алгоритма (ГА): решение задачи позиционирования в штатных ситуациях управления достигалось в большинстве экспериментов, однако в непредвиденных ситуациях управления (как во внешних, так и во внутренних) решение было достигнуто менее чем в трети экспериментов.
Применение технологий мягких вычислений для проектирования интеллектуальной системы управления (ИСУ) с регулируемыми коэффициентами ПИД-регулятора (без разрушения нижнего исполнительного уровня) с использованием такого инструментария, как оптимизатор БЗ (ОБЗ) на мягких вычислениях, позволило значительно повысить процент решения задач управления как в штатных, так и в непредвиденных ситуациях. Общая оценка управления при использовании ИСУ на ОБЗ на мягких вычислениях увеличилась в 1,7 раза по сравнению с системой управления на основе ГА и в 3 раза по сравнению с системой управления на основе ПИД-регулятора.
При работе ИСУ на ОБЗ на мягких вычислениях быстродействие увеличилось более чем в 10 раз по сравнению с системами управления с постоянными коэффициентами (на основе ПИД-регулятора и с использованием ГА), но в целом осталось достаточно низким.
Ввиду того, что рассматриваемый ОУ – робот-манипулятор с семью степенями свободы – сложен, ИСУ на ОБЗ на мягких вычислениях была организована с разделением управления. Однако декомпозиция управления привела к рассогласованию работы и некоторому снижению качества управления. В настоящей статье рассматривается метод организации координационного управления без значительного увеличения сложности системы, предполагающий введение дополнительного обобщающего звена с применением технологий квантовых вычислений.
Организация координационного управления с применением технологий квантовых вычислений
В работе [1] описан новый вид квантового поискового алгоритма на обобщенном пространстве БЗ нечетких регуляторов (НР), спроектированных на основе технологий мягких вычислений, – квантовый нечеткий вывод (КНВ) для проектирования обобщенного робастного сигнала управления. Модель КНВ реализует самоорганизацию БЗ, основывается на физических законах теории квантовых вычислений [2–6] и использовании четырех операторов: суперпозиции, квантовой корреляции, интерференции и измерения.
В [7] была показана эффективность применения алгоритма КНВ для организации координационного управления роботом-манипулятором с тремя степенями свободы. Алгоритм КНВ выполняет следующую последовательность шагов.
1. Нормализация.
2. Кодирование: построение всех нормализованных состояний и вычисление амплитуд вероятностей ï0ñ и ï1ñ из соответствующих гистограмм.
3. Выбор типа квантовой корреляции для построения выходных сигналов управления. Рассматриваются три типа смешанных корреляций: пространственная, пространственно-временная и временная [1], а помимо этого – корреляции различного числа НР. Зависимость выходных сигналов определяется корреляцией наборов входных коэффициентов, где каждый набор является запутанным состоянием.
4. Построение суперпозиции запутанных состояний [8].
5. Измерение интеллектуального квантового состояния.
6. Декодирование и денормализация.
Создание КНВ производится с помощью интеллектуального инструментария – ОБЗ – на основе квантовых вычислений. Схема подключения блока КНВ в ИСУ подробно рассмотрена в [7].
В выбранной конфигурации структуры ИСУ реализованы семь НР, каждый из которых независимо от других управляет одним из семи звеньев. В качестве штатной ситуации управления для i-го НР выступает типовая ситуация управления, в условиях которой получен обучающий сигнал TSi.
Непредвиденные ситуации управления разделяются на внешние (принудительное изменение положения ОУ в начале или в процессе работы, изменение опорных сигналов и др.) и внутренние (изменения параметров компонентов системы управления – ограничения, шумы и задержки сигналов).
 Спроектированная авторами ИСУ на ОБЗ на мягких вычислениях может содержать информацию о семи ситуациях управления (штатных или непредвиденных) для каждого из звеньев. Например, в спроектированной ИСУ на ОБЗ на мягких вычислениях с разделенным управлением НР1 содержит информацию о штатной ситуации 1 (БЗ1) для звена 1, НР2 – о штатной ситуации 1 для звена 2 (БЗ2) и т.д. Блок КНВ, включенный в модель ИСУ на ОБЗ на мягких вычислениях, реализует самоорганизацию БЗ НР. В этом случае имеется возможность не только объединять информацию о штатной ситуации 1 для всех звеньев, но и извлекать дополнительную информацию (методами квантовых вычислений и квантовой теории информации) из реакции спроектированных БЗ для реализации робастного управления в штатных и непредвиденных ситуациях управления (которые не включены в существующие спроектированные БЗ). При этом сами БЗ, реакции которых используются для проектирования робастного управления, в нештатных ситуациях могут быть неробастными. Далее ИСУ с использованием КНВ будем называть ИСУ на основе ОБЗ на квантовых вычислениях.
Спроектированная авторами ИСУ на ОБЗ на мягких вычислениях может содержать информацию о семи ситуациях управления (штатных или непредвиденных) для каждого из звеньев. Например, в спроектированной ИСУ на ОБЗ на мягких вычислениях с разделенным управлением НР1 содержит информацию о штатной ситуации 1 (БЗ1) для звена 1, НР2 – о штатной ситуации 1 для звена 2 (БЗ2) и т.д. Блок КНВ, включенный в модель ИСУ на ОБЗ на мягких вычислениях, реализует самоорганизацию БЗ НР. В этом случае имеется возможность не только объединять информацию о штатной ситуации 1 для всех звеньев, но и извлекать дополнительную информацию (методами квантовых вычислений и квантовой теории информации) из реакции спроектированных БЗ для реализации робастного управления в штатных и непредвиденных ситуациях управления (которые не включены в существующие спроектированные БЗ). При этом сами БЗ, реакции которых используются для проектирования робастного управления, в нештатных ситуациях могут быть неробастными. Далее ИСУ с использованием КНВ будем называть ИСУ на основе ОБЗ на квантовых вычислениях.
Качество интеллектуальной системы управления с квантовым нечетким выводом
Для исследования качества систем управления были разработаны модели систем управления роботом-манипулятором с семью степенями свободы в среде MatLab/Simulink.
Исходная ИСУ на ОБЗ на мягких вычислениях содержит семь НР, каждый из которых может коррелировать с одним или несколькими НР системы.
В данной статье рассматриваются шесть комбинаций:
1) корреляция двух соседних нечетких БЗ: для управления i-м звеном манипулятора используется информация НРi и НРi+1 (см. рис. 1);
2) корреляция трех соседних нечетких БЗ: для управления i-м звеном манипулятора используется информация НРi, НРi+1 и НРi+2;
3) корреляция четырех соседних нечетких БЗ: для управления i-м звеном манипулятора используется информация НРi, НРi+1, НРi+2 и НРi+3;
4) корреляция пяти соседних нечетких БЗ: для управления i-м звеном манипулятора используется информация НРi, НРi+1, НРi+2, НРi+3, и НРi+4;
5) корреляция шести соседних нечетких БЗ: для управления i-м звеном манипулятора используется информация НРi, НРi+1, НРi+2, НРi+3, НРi+4 и НРi+5;
6) корреляция всех семи нечетких БЗ.
Для каждой из шести комбинаций рассмат- риваются пространственная, пространственно- временная и временная корреляции. В таблице 1 приведено сравнение работы ИСУ на ОБЗ на квантовых вычислениях для пространственных, пространственно-временных и временных корреляций соответственно для шести комбинаций коррелируемых НР (два соседних НР, три соседних НР и т.д.) и ИСУ на ОБЗ на мягких вычислениях.
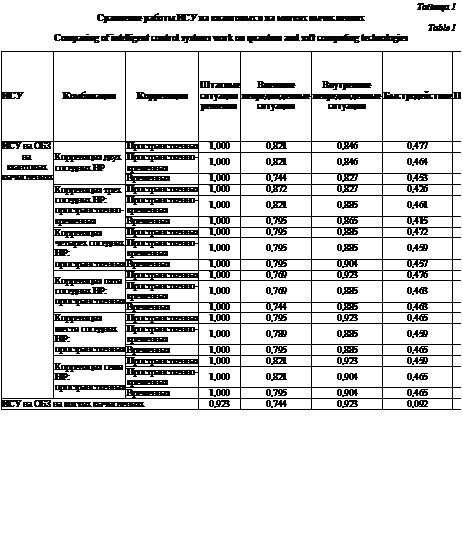
 Сравним работу ИСУ на ОБЗ на квантовых вычислениях при использовании отмеченных корреляций с работой ИСУ на ОБЗ на мягких вычислениях (табл. 1):
Сравним работу ИСУ на ОБЗ на квантовых вычислениях при использовании отмеченных корреляций с работой ИСУ на ОБЗ на мягких вычислениях (табл. 1):
– при любом варианте корреляции ИСУ на квантовых вычислениях обеспечивает решение задачи позиционирования в штатных ситуациях в отличие от ИСУ на мягких вычислениях;
– при решении задачи позиционирования в условиях внешних непредвиденных ситуаций лучшие результаты получены при использовании ИСУ на квантовых вычислениях с пространственной корреляцией двух соседних НР, пространственно-временной корреляцией трех соседних НР и пространственной корреляцией всех семи НР;
– при решении задачи позиционирования в условиях внутренних непредвиденных ситуаций улучшения при использовании ИСУ на квантовых вычислениях по сравнению с ИСУ на мягких вычислениях не получено;
– при использовании ИСУ на квантовых вычислениях по сравнению с ИСУ на мягких вычислениях критерий «быстродействие» улучшен в 5 раз;
– оценки по критериям «перерегулирование», «устойчивость», «время одной итерации» и «сложность реализации управления» практически не изменились;
– оценка общего управления по сравнению с ИСУ на ОБЗ на мягких вычислениях улучшается при использовании ИСУ на ОБЗ на квантовых вычислениях с использованием любого типа корреляции, однако наилучший результат достигается при использовании пространственной корреляции всех семи.
На рисунке 2 продемонстрирована работа манипулятора при использовании ИСУ на ОБЗ на мягких и квантовых вычислениях в условиях второй внешней непредвиденной ситуации управления (изменено начальное положение). Как видим, ИСУ на ОБЗ на квантовых вычислениях в условиях рассмотренных штатной и внешней непредвиденной ситуаций управления решает задачу точного позиционирования робота-манипулятора с семью степенями свободы в отличие от ИСУ на ОБЗ на мягких вычислениях.
Как было отмечено, при решении задачи позиционирования в условиях внутренних непредвиденных ситуаций улучшения при использовании ИСУ на квантовых вычислениях по сравнению с ИСУ на мягких вычислениях не получено.
Рассмотрим более подробно внутренние непредвиденные ситуации с внесением шумов в каналы управления и систему измерения. Усилим внутренние возмущения и сравним поведение ИСУ на мягких и на квантовых вычислениях.
Качество интеллектуальной системы управления с квантовым нечетким выводом в условиях сильных внутренних возмущающих воздействий
После рассмотрения таких внутренних непредвиденных ситуаций с внесением возмущающих воздействий, как внесение шумов в каналы управления (амплитуда шума = 1) и внесение погрешностей в систему измерения (1,5 градуса), опишем поведение систем управления в условиях значительно более сильных возмущающих воздействий.
Ранее решение задачи позиционирования определялось максимально точным позиционированием отдельных звеньев манипулятора. Однако в условиях сильных возмущающих воздействий точного позиционирования каждого звена добиться практически невозможно. По этой причине критерий качества «быстродействие» можно исключить из рассмотрения (время всегда будет равно числу допустимых итераций).
Поставим более общую задачу максимально точного позиционирования функционального устройства манипулятора. Для этого введем новый критерий качества – метрическая ошибка позиционирования функционального устройства EEP (End Effector Positioning):


где {X, Y, Z} – координаты достигнутой точки; {Xref, Yref, Zref} – координаты желаемой точки; N – число экспериментов; EEPmax – максимальная метрическая ошибка из оцениваемой серии экспериментов.
В соответствии с введенными обновлениями система критериев качества для оценки работы систем управления в условиях сильных внутренних возмущающих воздействий будет следующей.
1. Метрическая ошибка позиционирования функционального устройства EEP.
2. Относительное значение перерегулирования σ.
3. Относительная ошибка позиционирования звеньев ε.
4. Время одной итерации t.
5. Сложность реализации управления P.
6. Общая оценка управления FCB=w1×P[EEP]+ +w2×P[s]+w3×P[e]+w4×P[t]+w5×P, где w=[0,4 0,1 0,1 0,2 0,2] – вектор весовых коэффициентов.
 Рассмотрим непредвиденную ситуацию с внесением сильного возмущающего воздействия в каналы управления. Ранее уже была рассмотрена внутренняя непредвиденная ситуация с внесением в каналы управления случайных шумов с амплитудой = 1. Увеличим амплитуду вносимых случайных шумов до 10.
Рассмотрим непредвиденную ситуацию с внесением сильного возмущающего воздействия в каналы управления. Ранее уже была рассмотрена внутренняя непредвиденная ситуация с внесением в каналы управления случайных шумов с амплитудой = 1. Увеличим амплитуду вносимых случайных шумов до 10.
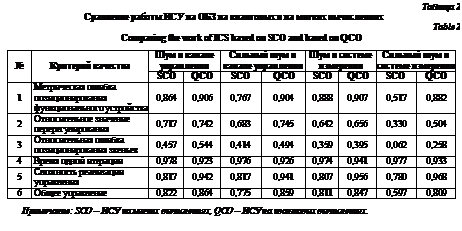
Проводим следующую серию экспериментов: для 13 точек рабочего пространства манипулятора генерируется 30 случайных шумов. Сгенерированные шумы вносятся в канал управления ИСУ на ОБЗ на мягких вычислениях с разделенным управлением и ИСУ на ОБЗ на квантовых вычислениях. По результатам 390 экспериментов сравниваем работу ИСУ на ОБЗ на мягких и на квантовых вычислениях в соответствии с введенной системой критериев качества (табл. 2).
Как видим, ИСУ на ОБЗ на квантовых вычислениях по всем критериям (за исключением времени одной итерации) превосходит ИСУ на ОБЗ на мягких вычислениях. В целом ошибка позиционирования функционального устройства при использовании только мягких вычислений не превышает 0,3 метра при длине одного звена 1 м.
Сгенерируем шумы, при которых метрическая ошибка позиционирования функционального устройства при работе ИСУ на ОБЗ на мягких вычислениях составит более 0,5 метра, и при тех же шумах оценим поведение ИСУ на квантовых вычислениях. Для этого увеличим амплитуду шумов, вносимых в каналы управления, до 100. Для 13 точек рабочего пространства манипулятора генерируется 5 случайных шумов.
Сгенерированные шумы вносятся в каналы управления ИСУ на ОБЗ на мягких вычислениях с разделенным управлением и ИСУ на ОБЗ на квантовых вычислениях. По результатам 65 экспериментов сравниваем работу ИСУ на ОБЗ на мягких и ИСУ на ОБЗ на квантовых вычислениях в соответствии с введенной системой критериев качества (табл. 2).
Как видим, ИСУ на ОБЗ на квантовых вычислениях по всем критериям (за исключением времени одной итерации) превосходит ИСУ на ОБЗ на мягких вычислениях. В рассмотренных непредвиденных ситуациях с внесением сильных шумов в каналы управления ИСУ на ОБЗ на квантовых вычислениях показала преимущество перед ИСУ на ОБЗ на мягких вычислениях.
Рассмотрим непредвиденную ситуацию с внесением сильного возмущающего воздействия в систему измерения. Ранее уже была рассмотрена внутренняя непредвиденная ситуация с внесением в систему измерения случайных шумов с амплитудой = 1,5. Увеличим амплитуду вносимых случайных шумов до 5 градусов.
Для 13 точек рабочего пространства генерируется 30 случайных шумов. Сгенерированные шумы вносятся в систему измерения ИСУ на ОБЗ на мягких вычислениях с разделенным управлением и ИСУ на ОБЗ на квантовых вычислениях. По результатам 380 экспериментов сравниваем работу ИСУ на ОБЗ на мягких и ИСУ на ОБЗ на квантовых вычислениях (табл. 2).
Как видим, ИСУ на ОБЗ на квантовых вычислениях по всем критериям (за исключением времени одной итерации) превосходит ИСУ на ОБЗ на мягких вычислениях.
Применение ИСУ на ОБЗ на квантовых вычислениях позволяет несколько улучшить работу по сравнению с ИСУ на ОБЗ на мягких вычислениях, однако улучшение незначительное. В целом ошибка позиционирования функционального устройства при использовании только мягких вычислений не превышает 0,3 метра при длине одного звена 1 м.
Сгенерируем шумы, при которых метрическая ошибка позиционирования функционального устройства при работе ИСУ на ОБЗ на мягких вычислениях составит более 1,5–2 метров, и при тех же шумах оценим поведение ИСУ на квантовых вычислениях. Для этого увеличим амплитуду шумов, вносимых в систему измерения, до 10 градусов.
Для 13 точек рабочего пространства манипулятора генерируются 5 случайных шумов. Сгенерированные шумы вносятся в систему измерения ИСУ на ОБЗ на мягких вычислениях с разделенным управлением и ИСУ на ОБЗ на квантовых вычислениях. По результатам 65 экспериментов сравниваем работу ИСУ на ОБЗ на мягких и ИСУ на ОБЗ на квантовых вычислениях (табл. 2). Видим, что ИСУ на ОБЗ на квантовых вычислениях по всем критериям (за исключением времени одной итерации) превосходит ИСУ на ОБЗ на мягких вычислениях.
 Рассмотрим пример влияния шума в системе измерения на работу ИСУ на мягких и на квантовых вычислениях. На рисунке 3 приведено положение манипулятора при работе ИСУ на мягких (слева) и на квантовых вычислениях (справа).
Рассмотрим пример влияния шума в системе измерения на работу ИСУ на мягких и на квантовых вычислениях. На рисунке 3 приведено положение манипулятора при работе ИСУ на мягких (слева) и на квантовых вычислениях (справа).
В рассмотренных непредвиденных ситуациях с внесением сильных шумов в систему измерения ИСУ на ОБЗ на квантовых вычислениях показала преимущество перед ИСУ на ОБЗ на мягких вычислениях.
Подытоживая, отметим, что на примере сложного ОУ – робота-манипулятора с семью степенями свободы – были рассмотрены принципы проектирования систем управления с применением технологий квантовых вычислений.
На уровне моделирования (с использованием пакета MatLab/Simulink) продемонстрировано, что включение обобщающего звена КНВ в ИСУ на основе ОБЗ на мягких вычислениях позволило обеспечить полное решение задачи позиционирования в штатных ситуациях управления при применении ИСУ на ОБЗ на квантовых вычислениях в отличие от ИСУ на ОБЗ на мягких вычислениях; улучшить показатель решения задачи точного позиционирования в условиях внешних непредвиденных ситуаций управления; значительно улучшить показатель точности позиционирования функционального устройства в условиях сильных внутренних возмущений и в 5 раз показатель быстродействия, а также уменьшить относительную ошибку позиционирования звеньев.
Литература
1. Литвинцева Л.В., Ульянов И.С., Ульянов С.В., Ульянов С.С. Квантовый нечеткий вывод для создания баз знаний в робастных интеллектуальных регуляторах // Изв. РАН: Теория и системы управления. 2007. № 6. C. 71–126.
2. Nielsen M.A., Chuang I.L. Quantum computation and quantum information. UK, Cambridge, Cambridge Univ. Press, 2000, 700 p.
3. Chen G., Diao С. Mathematical Theory of Quantum Computation. NY, Chapman Hall CRC, 2013, 320 p.
4. Yanofsky N.S., Mannucci M.A. Quantum Computing for Computer Scientists. Cambridge, Cambridge Univ. Press, 2008, 368 p.
5. Jaeger G. Quantum Information: An overview. NY: Springer Verlag, 2007, 284 p.
6. Marinescu D.C., Marinescu G.M. Approaching quantum computing. NJ, Pearson Prentice Hall, 2005, 400 p.
7. Николаева А.В., Ульянов С.В. Интеллектуальное управление роботом-манипулятором на основе квантовых мягких вычислений // Программные продукты и системы. 2014. № 1. С. 108–116.
8. Jozsa R., Linden N. On the role of entanglement in quantum computational speed-up. Proc. of the Royal Society, 2003, vol. 459, no. 2036, pp. 2011–2032.
References
1. Litvintseva L.V., Ulyanov I.S., Ulyanov S.V., Ulya- nov S.S. Quantum fuzzy inference for knowledge base design in robust intelligent controllers. Izvestiya RAN. Teoriya i sistemy upravleniya [Journ. of Computer and Systems Sciences Int.]. 2007, no. 6, pp. 71–126.
2. Nielsen M.A., Chuang I.L. Quantum computation and quantum information. UK, Cambridge, Univ. Press, 2000, 700 p.
3. Chen G., Diao С. Mathematical theory of quantum computation. NY, Chapman Hall CRC, 2013, 320 p.
4. Yanofsky N.S., Mannucci M.A. Quantum computing for computer scientists. Cambridge, Univ. Press, 2008, 368 p.
5. Jaeger G. Quantum information: an overview. NY, Sprin- ger Verlag Publ., 2007, 284 p.
6. Marinescu D.C., Marinescu G.M. Approaching quantum computing. NJ, Pearson Prentice Hall Publ., 2005, 400 p.
7. Nikolaeva A.V., Ulyanov S.V. Intelligent robust control of a robot manipulator based on quantum soft computing. Programmnye produkty i sistemy [Software & Systems]. 2014, no. 1, pp. 108–116.
8. Jozsa R., Linden N. On the role of entanglement in quantum computational speed-up. Proc. of the Royal Society. 2003, vol. 459, no. 2036, pp. 2011–2032.



 Сравним работу ИСУ на ОБЗ на квантовых вычислениях при использовании отмеченных корреляций с работой ИСУ на ОБЗ на мягких вычислениях (табл. 1):
Сравним работу ИСУ на ОБЗ на квантовых вычислениях при использовании отмеченных корреляций с работой ИСУ на ОБЗ на мягких вычислениях (табл. 1):

 Рассмотрим непредвиденную ситуацию с внесением сильного возмущающего воздействия в каналы управления. Ранее уже была рассмотрена внутренняя непредвиденная ситуация с внесением в каналы управления случайных шумов с амплитудой = 1. Увеличим амплитуду вносимых случайных шумов до 10.
Рассмотрим непредвиденную ситуацию с внесением сильного возмущающего воздействия в каналы управления. Ранее уже была рассмотрена внутренняя непредвиденная ситуация с внесением в каналы управления случайных шумов с амплитудой = 1. Увеличим амплитуду вносимых случайных шумов до 10.