Численное моделирование химически реактивных молекулярных систем актуально для целого ряда прикладных научных задач. Для небольших химических соединений (до 100 атомов) это можно делать методами квантовой механики (ab initio), однако для моделирования более крупных структур данные методы непригодны из-за высокой ресурсоемкости. Традиционные молекулярно-динамические методы, которые обычно используются для крупномасштабных систем, как правило, основаны на классическом потенциале силовых полей и не позволяют хорошо воспроизводить многокомпонентные химически реактивные системы. Поэтому в своей работе, связанной с изучением систем хранения водорода, для моделирования деструкции гидридов легких металлов с выделением водорода мы используем комбинированный подход. Он базируется на потенциале реактивных силовых полей ReaxFF (Reactive Force Field) [1, 2], параметризация которого выполняется на основе точных квантовых расчетов для малых кластеров. Отметим, что потенциал ReaxFF изначально разрабатывался для описания химической реактивности, диссоциации и формирования химических связей, дефектов, поверхностных эффектов и др. Такой подход позволяет на современных высокопроизводительных параллельных вычислительных кластерах моделировать развивающиеся во времени системы с числом атомов порядка 106–108.
Программная реализация потенциала имеется в ПО ADF/BAND (лицензионный платный па- кет) [3] и LAMMPS (свободно распространяемый пакет) [4]. Для адекватных расчетов с использованием ReaxFF применительно к системе конкретного типа (например углеводороды или гидриды металлов) предварительно необходимо осуществить достаточно трудоемкий процесс поиска/оптимизации многочисленных параметров этого потенциала, при которых он будет корректно описывать процессы, происходящие в этой системе. Однако в отличие от самого потенциала ReaxFF программ оптимизации его параметров в открытом доступе нет. Поэтому, опираясь на описание метода однопараметрического поиска [5] и реализацию потенциала ReaxFF в LAMMPS, авторами был разработан свой параллельный алгоритм оптимизации параметров, описание которого представлено в данной работе.
Потенциал ReaxFF. Форма МД-потенциала ReaxFF подобна используемой во многих нереактивных силовых полях, где энергия системы состоит из различных энергетических вкладов. Принципиальное отличие заключается в использовании не жесткого метода связывания, а метода порядков связей. Порядок связи характеризует кратность связи между конкретной парой атомов в соединении и выражается формулой
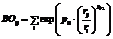 ,
,
где индекс l равен σ, π, ππ (типы ковалентной связи); rij – расстояние между атомами; pl1, pl2, rl – параметры [2]. Порядки связей, вычисляемые при численном моделировании для всех атомов непосредственно из межатомных расстояний и обновляемые на каждом шаге по времени, позволяют описать образование и диссоциацию связей во время моделирования. Общий вид потенциала [2] следующий:
EReaxFF({rij}, {rijk}, {rijkl}, {qi}, {BOij})=
=Ebond+Eover+Eunder+Eval+Epen+Ecoa+Etors+
+Econj+Ehbond+Elp+ EvdWaals+ECoulomb. (1)
Каждое слагаемое в правой части формулы отвечает за отдельный тип взаимодействия: ковалентное (характеризуется порядком химических связей, слагаемые Ebond, Eover, Eunder), трехчастичное (валентные углы, Eval, Epen, Ecoa), четырехчастичное (двугранные валентные углы, Etors, Econj), кулоновское (ECoulomb), ван-дер-ваальсовое (EvdWaals), водородные связи (Ehbond) и энергия неподеленных электронных пар (Elp).
Полная энергия является суммой функций относительных положений пар атомов rij, троек rijk и четверок rijkl. Более того, каждая из этих функций зависит от некоторого числа параметров, которые определяются тем, какие химические элементы взаимодействуют. Таким образом, весь потенциал зависит от многочисленных (в зависимости от сложности соединения их количество может быть более 100) параметров: EReaxFF=f(p1, p2, p3, …, pN). Анализ подробного вида всех слагаемых в формуле (1) позволяет сделать вывод, что EReaxFF и его первая производная являются непрерывными функциями координат атомов даже при химических реакциях [2].
Метод однопараметрической оптимизации. Реализация алгоритма оптимизации параметров основана на методе однопараметрического поис- ка [5]. Данные, по которым производится поиск (оптимизирующий набор, training set), получаются из расчетов простых моделей химических соединений (до 50 атомов) методами квантовой химии или же берутся из эксперимента. Данными оптимизации являются геометрические характеристики молекул (расстояния между атомами, валентные углы, двугранные углы), колебательные частоты, эффективные заряды атомов и энергии связи соединений, а также какие-либо другие характеристики, которые можно вычислить методами молекулярной динамики, а затем сравнить с данными оптимизирующего набора. Процедура однопараметрического поиска состоит в изменении параметров потенциала для минимизации суммы квадратов:
 (2)
(2)
Здесь xiQC/Lit – данные оптимизирующего набора (конкретные характеристики модели или молекулы, полученные методами квантовой химии или из литературы (эксперимента)); xiReaxFF – вычисленные с использованием ReaxFF значения, соответствующие этим характеристикам; σi – критерий приемлемости, который имеет размерность xi и характеризует вклад разности xiQC/Lit–xiReaxFF в сумму квадратов. Сумма (2) представляет собой так называемую функцию ошибки – отклонение расчетов ReaxFF от данных оптимизирующего набора. Каждое xiReaxFF зависит от параметров потенциала p1, ..., pN, поэтому и Err является функцией этих параметров.
Важно отметить, что для вычисления значения xiReaxFF для каждой модели оптимизирующего набора при конкретных значениях параметров необходимо провести поиск минимума потенциальной энергии (1) этой модели как функции координат составляющих ее атомов с использованием какого-либо многопараметрического метода, например метода сопряженных градиентов. Эту процедуру не следует путать с процедурой минимизации суммы (2) как функции параметров потенциала.
Основой метода однопараметрической оптимизации является параболическая экстраполяция, которая выполняется поочередно для каждого параметра pk при фиксированных остальных. На малых интервалах зависимость между ошибкой Err и значением каждого параметра pk можно считать параболической, поэтому для определения оптимального значения параметра необходимо вычислить Err при трех различных значениях: pk, pk(1–δk), pk(1+δk), где δk<<1 – множитель смещения. Для построенного по этим точкам полинома второй степени методом экстраполяции производится поиск значения pkopt, соответствующего минимальному значению полинома на интервале [pk(1–Δk), pk(1+Δk)], где δk≤Δk<<1 – множитель экстраполяции.
Одна итерация программы состоит в выполнении описанной процедуры один раз для каждого pk из списка. Так как большинство параметров в силовом поле ReaxFF связаны между собой, оптимальное значение каждого параметра сдвигается каждый раз, когда другой параметр изменяется. Это означает, что процесс оптимизации должен быть повторен до тех пор, пока Err не перестанет уменьшаться, что определяется критерием сходимости ε. Отметим, что для каждого параметра pk должен быть задан допустимый интервал изменения [Dkmin, Dkmax], чтобы избежать сходимости в нереалистичную область.
Также следует отметить, что метод однопараметрического поиска гарантирует сходимость в минимум, но этот минимум может оказаться не абсолютным, а только локальным.
Описание программы оптимизации параметров потенциала ReaxFF. Блок-схема алгоритма разработанной программы показана на рисунке. Общая структура программы включает инициализацию, чтение входных данных, два вложенных цикла, запись промежуточных и выходных результатов. Внешний цикл организует итерации по полному набору параметров, а внутренний обеспечивает процедуру экстраполяции по параметру pk. Внутренний цикл содержит расчеты с потенциалом ReaxFF всех моделей оптимизирующего набора и является весьма ресурсоемким. Он распараллелен с помощью технологии MPI, что позволяет запускать программу на вычислительных узлах кластера.
 На первой стадии программа инициализирует три процесса и производит чтение из файлов входных параметров: начальных значений параметров p10, ..., pN0, величин множителей смещения δ1, ..., δN, величин множителей экстраполяции Δ1, ..., ΔN, допустимых границ изменения параметров потенциала Dkmin и Dkmax, k=1, ..., N, максимального числа итераций M и критерия сходимости ε. Также обрабатываются входной файл молекулярно-динамического симулятора LAMMPS и файлы моделей с их характеристиками xiQC/Lit и начальными (взятыми из квантово-химических расчетов) конфигурациями атомов.
На первой стадии программа инициализирует три процесса и производит чтение из файлов входных параметров: начальных значений параметров p10, ..., pN0, величин множителей смещения δ1, ..., δN, величин множителей экстраполяции Δ1, ..., ΔN, допустимых границ изменения параметров потенциала Dkmin и Dkmax, k=1, ..., N, максимального числа итераций M и критерия сходимости ε. Также обрабатываются входной файл молекулярно-динамического симулятора LAMMPS и файлы моделей с их характеристиками xiQC/Lit и начальными (взятыми из квантово-химических расчетов) конфигурациями атомов.
Внешний цикл организует итерации по набору параметров. За один шаг этого цикла обеспечивается проход по всему списку p1, ..., pN, и для каждого pk выполняется одна процедура экстраполяции. Результат одной итерации – новый набор {pkt}, который будет использоваться в следующей итерации. Цикл завершается, если на очередном шаге t будет удовлетворено условие сходимости |Errt–Errt-1|<ε или достигнут лимит количества итераций M.
Внутренний цикл, предназначенный для самой трудоемкой процедуры экстраполяции, выполняется параллельно. На этом этапе каждый из трех процессов получает свое значение параметра (pk, pk(1–δk), pk(1+δk)) и вычисляет для него значение функции ошибки (2) (на рисунке Err-, Err0 и Err+). Для этого используется вызов симулятора LAMMPS с реализацией потенциала ReaxFF, собранного в качестве библиотеки. С помощью библиотеки LAMMPS происходит поиск минимума потенциальной энергии (1) моделей оптимизирующего набора при заданных значениях параметров как функции координат составляющих их атомов. Отметим, что алгоритмы, входящие в состав библиотеки LAMMPS, сходятся зачастую не к минимуму, а к седловой точке некоторого порядка. Поэтому к библиотечным методам минимизации пакета LAMMPS авторы добавили свой модуль для вычисления матрицы Гессе (второй производной потенциала по координатам атомов). Его использование помогает избежать сходимости в седловые точки и гарантирует попадание в минимум. После этого вычисляются характеристики моделей оптимизирующего набора xiReaxFF и значения функции (2) Err-, Err0 и Err+. На следующем шаге алгоритма процесс 0 получает от процессов 1 и 2 вычисленные ими значения Err- и Err+ и выполняет процедуру параболической экстраполяции (Fextr на рисунке). Полученное оптимальное значение параметра pkt записывается в журнал и выходной файл параметров потенциала. Последовательность повторяется для всех N параметров в списке, после чего последнее оптимальное значение функции ошибки записывается в память как Errt.
На выходе программы получаются два текстовых файла: файл с оптимизированными параметрами потенциала и log-файл (журнал работы программы). Журнал программы содержит подробную информацию обо всех итерациях внутреннего цикла. На каждой итерации в него записываются имя параметра; три его значения; ошибки (2) этих значений; коэффициенты экстраполяционной параболы; экстремум параболы; значение параметра, полученное экстраполяцией; экстраполированное и вычисленное значения ошибки параметра; окончательное значение параметра, выбранное как оптимальное; его ошибка (2).
Журнал позволяет контролировать ход процесса оптимизации, при необходимости остановить программу и продолжить ее выполнение с произвольной итерации.
Структура пакета. Исходный код программы разработан на языке C и имеет модульную структуру. Программный пакет собран и доступен в виде архива с исходными кодами, инструкцией и сценарием компиляции, документацией для пользователя и примерами входных файлов.
Тестирование и использование. Функциональность программы проверялась на примере оптимизации параметров алюминия и его гидридов. За начальное приближение при оптимизации были взяты параметры, включенные в дистрибутив пакета LAMMPS, которые следует считать довольно грубыми, поскольку они дают плохие результаты для решеток металла и его гидридов.
Для оптимизации параметров мы использовали набор, в который вошли кластеры чистого алюминия (Al2 – Al8, Al13), кластеры гидрида (AlnH3n, n=1, ..., 8), а также кристаллы α- β- и γ-модификаций гидрида алюминия [6, 7], порожденные из ячеек с периодическими условиями. Добавление в набор бесконечных кристаллических структур позволило учесть уравнение состояния, то есть зависимость энергии кристаллов от объема ячейки. В общей сложности набор включал 56 структур.
Всего в оптимизации участвовало 79 параметров потенциала. Одна итерация процедуры оптимизации (по одному параметру) на вычислительном кластере занимала в данном случае около 4 часов. За одну итерацию величина ошибки уменьшалась на значение от 0,1 до 1 % по сравнению с предыдущей итерацией. Программа совершила около 4 000 итераций, за это время величина ошибки сократилась приблизительно в 500 раз.
Для проверки качества полученных параметров было выполнено моделирование кристаллических решеток гидридов алюминия при начальных и оптимизированных параметрах с целью сравнения их стабильности, плотности и регулярности структуры при комнатной температуре. Все исходные решетки синтезированы по данным расчетов методами квантовой химии для каждой из модификаций, каждая система содержит около 4 000 атомов и помещается в вакуум. Численный эксперимент состоял в наблюдении за поведением каждой системы во времени при постоянной температуре (300 К), которая поддерживалась термостатом Нозе–Хувера.
При моделировании с начальным набором параметров кристаллическая структура всех гид- ридов распалась, плотность вещества снизилась почти в два раза. На оптимизированном наборе параметров регулярная структура полностью сохранилась, хотя постоянные решеток кристаллов немного изменились (1–6 %). В конце эксперимента плотности кристаллов при оптимизированных параметрах отличались от реальных на 9, 14 и 4 % для α-, β- и γ-модификаций соответственно.
Таким образом, разработанная программа поиска параметров потенциала ReaxFF достаточно универсальна и может быть использована для систем атомов произвольного типа. Оптимизирующий набор может включать любые соединения, хотя набор характеристик этих соединений пока ограничен: в него входят длины связей, величины валентных углов и двугранных валентных углов, энергии атомизации, теплоты образования и эффективные заряды атомов. Модульная структура кода позволяет легко добавлять расширения при необходимости учета дополнительных условий или характеристик моделей. Применимость разработанных методов для оптимизации парамет- ров потенциала ReaxFF продемонстрирована для MД-моделирования гидридов алюминия.
Литература
1. van Duin A.C.T., Dasgupta S., Lorant F., Goddard W.A. III ReaxFF: A Reactive Force Field for Hydrocarbons. Journ. of Physical Chemistry A., 2001, vol. 105, pp. 9396–9409.
2. Nomura K., Kalia R.K., Nakano A., Vashishta P. A scalable parallel algorithm for large-scale reactive force-field molecular dynamics simulations. Computer Physics Communications, 2008, vol. 178, pp. 73–87.
3. ADF.URL: http://www.scm.com (дата обращения: 22 февраля 2014).
4. Программный пакет LAMMPS. URL: http://lammps.sandia.gov (дата обращения: 22 февраля 2012).
5. van Duin A.C.T., Baas J.M.A., van de Graaf B. Delft Molecular Mechanics: A New Approach to Hydrocarbon Force Fields. Journ. of the Chemical Society, Faraday Transactions, 1994, vol. 90, pp. 2881–2895.
6. Turley J.W., Rinn H.W. Inorg. Chem., 1969, vol. 8, p. 18.
7. Yartys V.A., Denys R.V., Maehlen J.P., Frommen C., Fichtner M., Bulychev B.M. // Inorganic Chemistry, 2007, vol. 46, pp. 1051–1055.
References
1. van Duin A.C.T., Dasgupta S., Lorant F., Goddard W.A. III ReaxFF: a reactive force field for hydrocarbons. Journ. of Phy- sical Chemistry A. 2001, vol. 105, pp. 9396–9409.
2. Nomura K., Kalia R.K., Nakano A., Vashishta P. A scalable parallel algorithm for large-scale reactive force-field molecular dynamics simulations. Computer Physics Communications. 2008, vol. 178, pp. 73–87.
3. ADF. Available at: http://www.scm.com (accessed Feb. 22, 2014).
4. LAMMPS Molecular Dynamics Simulator. Available at: http://lammps.sandia.gov (accessed Feb. 22, 2014).
5. van Duin A.C.T., Baas J.M.A., van de Graaf B. Delft Molecular Mechanics: a new approach to hydrocarbon force fields. Journ. of the Chemical Society, Faraday Transactions. 1994, vol. 90, pp. 2881–2895.
6. Turley J.W., Rinn H.W. Inorg. Chem. 1969, vol. 8, p. 18.
7. Yartys V.A., Denys R.V., Maehlen J.P., Frommen C., Fichtner M., Bulychev B.M. Inorganic Chemistry. 2007, vol. 46, pp. 1051–1055.



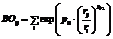 ,
, (2)
(2)
