Современные САПР технологических процессов (ТП) ковки различных видов поковок на молотах и прессах [1–3], как правило, предусматривают реализацию двух этапов проектирования. На первом этапе проектирование ТП осуществляется в автоматическом режиме на основе алгоритмов, в соответствии с которыми входная информация о детали последовательно преобразуется в технологическую документацию, представляющую чертеж поковки и карту ТП ковки.
На втором этапе пользователь анализирует полученную карту ТП ковки и при необходимости вносит корректировки в результаты проектирования в режиме активного диалога. При этом предусматривается корректировка двумя способами: автоматический поиск подходящих вариантов решений в БД [3] и изменение решений самим пользователем.
В данной статье рассматриваются вопросы, связанные с реализацией второго варианта внесения корректировок в результаты проектирования на примере САПР ТП ковки валов на прессах.
Необходимость предоставления пользователю возможности внесения корректировок обусловлена сложностью и недостаточной формализацией предметной области, вследствие чего технологические решения, касающиеся процесса проектирования, не только различны на разных предприятиях, но и в рамках одного предприятия зачастую неоднозначны и даже противоречивы.
Поскольку все решения, отраженные в карте ТП ковки, взаимосвязаны, корректировка любого из них, как правило, требует повторного перепроектирования всего ТП с учетом внесенных ранее корректировок. В этом смысле речь идет об управлении процессом проектирования. Концептуальная схема, в рамках которой формулируется любая задача управления, представлена в [4]. В поставленной задаче эта схема может быть интерпретирована следующим образом.
Объектом управления является процесс проектирования технологии ковки, который всегда происходит в определенных производственных условиях, то есть в конкретной среде проектирования. В качестве модели объекта управления выступает карта ТП ковки, которая отражает все особенности спроектированного ТП и является одним из возможных решений поставленной задачи.
Цель управления объектом состоит в получении технологии изготовления годной поковки с минимальными материальными и энергетическими затратами.
Если полученное решение (модель объекта управления) удовлетворяет требованиям, предъявляемым пользователем, то поставленная цель достигнута. Если цель не достигается, необходимо произвести корректировку решения, реализуя некоторое воздействие на модель объекта управления. Это воздействие выбирается на основе среды проектирования и модели объекта управления и выполняется блоком реализации решений, являющимся совокупностью программ САПР ТП ковки. Воздействие переводит модель объекта управления в новое состояние и может вызвать некоторые несоответствия со средой проектирования. Например, исключение операции осадки выбранного слитка может потребовать его замены на слиток большего веса, который имеется в БД системы, но на предприятии в данный момент отсутствует. Пользователь может оценить это, наблюдая модель объекта управления и среду проектирования и сравнивая сложившуюся реальную ситуацию с целью проектирования. Результат такого наблюдения и сравнения инициирует либо новые воздействия на модель объекта управления, когда цель не достигается, либо завершение работы при достижении цели.
Очевидно, что на основе среды проектирования и модели объекта управления можно сформировать множество альтернатив (вариантов воздействия на объект управления) и для каждой из них определить, насколько данное воздействие приближает разработчика техпроцесса к достижению поставленной цели. При этом оказываемые воздействия (корректировки пользователя) всегда должны находиться в определенных технологических границах.
Процесс проектирования технологии ковки валов на прессах является достаточно сложным из-за того, что в процессе ковки применяются, как правило, промежуточные подогревы металла в печи. Для каждого этапа подогрева в печи (называемого выносом) необходимо проектировать промежуточную конфигурацию поковки и технологию ее ковки (переходы) с учетом технологических ограничений, оговоренных в технологических инструкциях предприятий. Однако на практике это не всегда возможно.
 Поясним это на примере. На рисунке 1 приведена укрупненная типовая схема переходов ковки валов на прессах.
Поясним это на примере. На рисунке 1 приведена укрупненная типовая схема переходов ковки валов на прессах.
Все технологические переходы ковки можно условно разбить на две группы: подготовительные (переходы I, II) и основные (переходы III, IV). К подготовительным отнесем переходы, применяемые при ковке слитка, к основным – переходы, во время которых происходит непосредственное формирование конечной поковки (вала).
Каждому переходу соответствует определенная характеристика степени деформации (Us, Uk, U1, U2, U3), называемая уковом, которая указывается над соответствующим эскизом.
Технологические рекомендации по выбору подготовительных и основных переходов, вариантов их завершения и размеров соответствующих заготовок приведены в работе [5].
Основной операцией в переходе I (см. рис. 1) является биллетировка слитка, когда исходному слитку придается форма усеченного конуса, который принято называть биллетом. Биллетировка слитка применяется для того, чтобы сбить окалину и грани. Методика расчета размеров биллета достаточно однозначно описана в литературе.
При определении размеров осаженного слитка (переход II на рис. 1) необходимо учитывать два ограничения: минимально допустимый уков при осадке  , определяемый как отношение длины биллета Lb к высоте осаженного слитка Hs:
, определяемый как отношение длины биллета Lb к высоте осаженного слитка Hs:
 , (1)
, (1)
и условие технологичности слитка T, определяемое как минимально допустимое отношение высоты осаженного слитка Hs к его диаметру:
 (2)
(2)
На практике обычно принимают  T=0,6.
T=0,6.
Очевидно, что максимально допустимая высота осаженного слитка  определяется из условия (1) по формуле
определяется из условия (1) по формуле  , а минимально допустимая высота
, а минимально допустимая высота 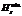 – из условия (2) по формуле
– из условия (2) по формуле  где
где  ; Vs – объем осаженного слитка с учетом угара биллета.
; Vs – объем осаженного слитка с учетом угара биллета.
Таким образом, 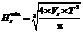 .
.
Минимально и максимально допустимые диаметры  осаженного слитка определяются из условия постоянства объема Vs по формулам:
осаженного слитка определяются из условия постоянства объема Vs по формулам:  ,
, .
.
Следующей ковочной операцией в переходе II (рис. 1) является протяжка осаженного слитка в цилиндрическую заготовку. Границы размеров цилиндрической заготовки связаны с минимально и максимально допустимыми уковами для этой ковочной операции  неравенствами
неравенствами
 (3)
(3)
Значение укова  определяется технологическими инструкциями (в операции протяжки обычно равно 2). Величина
определяется технологическими инструкциями (в операции протяжки обычно равно 2). Величина 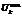 вычисляется по формуле
вычисляется по формуле 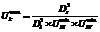 , где
, где  – квадрат наибольшего диаметра ступеней готовой поковки вала,
– квадрат наибольшего диаметра ступеней готовой поковки вала,  – минимально допустимые уковы в III и IV переходах (рис. 1). На практике при ковке валов обычно принимают
– минимально допустимые уковы в III и IV переходах (рис. 1). На практике при ковке валов обычно принимают  ,
, 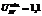 .
.
Из условия (3) следует
 ,
,  .
.
Определенные таким образом границы раз- меров осаженного слитка, цилиндрической заготовки и ряда других параметров процесса ковки образуют доверительные интервалы, полностью соответствующие технологическим ограничениям, гарантирующим получение качественной поковки. Проектирование на первом этапе выполняется со строгим соблюдением этих интервалов.
Однако анализ карт ТП ковки валов, уже прошедших практическую апробацию на различных металлургических предприятиях, показал, что технологи, разрабатывая технологию ковки и опираясь на свой производственный опыт, иногда вынуждены принимать решения, несколько отличающиеся от рекомендованных и все же позволяющие в итоге получить качественную поковку. Так, например, встречаются карты ТП, в которых значения Us=1,8, T=0,5, Uk=1,25 и т.д.
К таким же примерам можно отнести расчет размеров ступеней поковки типа вала ротора в предпоследнем и последнем выносах, когда длина ротора превышает 10 метров и по технологическим ограничениям не позволяет отковать все ступени в окончательные размеры в последнем выносе, не нарушая температурный интервал ковки из-за разности в скоростях ковки и остывания заготовки. На практике в этом случае поступают так: в предпоследнем выносе отковывают в окончательные размеры только половину вала, полученную заготовку снова нагревают и в последнем выносе отковывают вторую половину. При этом уковы ступеней первой половины вала в последнем выносе оказываются равными единице, что противоречит ограничению по минимально допустимым уковам ступеней поковки в последнем выносе.
Таким образом, можно прийти к выводу, что сами границы технологических ограничений всегда находятся в определенном диапазоне своих значений и необходимо предоставить пользователю возможность вносить корректировки в решения системы с незначительным выходом за границы доверительных интервалов.
Согласно теории нечеткой логики, термин «незначительный выход» можно отнести к классу нечетких понятий, на которых построена теория приближенных рассуждений [6]. В основе приближенных рассуждений лежат логические правила вида «если …, то …», в которых посылки и выводы являются нечеткими понятиями. Можно привести следующий пример так называемого правила вывода modus ponens в нечеткой логике в рассматриваемой предметной области.
Посылка 1:  .
.
Вывод 1: протянутая цилиндрическая заготовка позволяет получить годную поковку.
Посылка 2:  на незначительную величину.
на незначительную величину.
Вывод 2: протянутая цилиндрическая заготовка позволяет получить практически годную поковку.
Такого рода приближенные рассуждения лежат в основе способности человека принимать решения в сложной и не полностью определенной среде. Вывод такого обобщения для решения конкретной прикладной задачи зависит от свойств предметной области и инженерного опыта пользователя системы.
Накопленный опыт работы позволяет утверждать, что задача автоматизации проектирования технологии ковки на прессах в условиях неопределенности при принятии решений может быть успешно решена путем повышения интеллектуальности системы за счет применения аппарата теории нечетких множеств [7–9].
 Как известно, в нечетком множестве в отличие от классических множеств каждый элемент может принадлежать множеству частично. Степень принадлежности конкретного элемента x* нечеткому множеству X характеризуется коэффициентом принадлежности muX(x*), являющимся действительным числом и принимающим значение в интервале [0, 1]. Равенство этого коэффициента 1 означает 100-процентную принадлежность элемента x* к множеству X, а равенство 0 – отсутствие элемента x* в множестве X. Отображение всего множества элементов x во множество значений muX(x) образует функцию принадлежности muX(x). В теории нечетких множеств наибольшее распространение получили функции принадлежности гауссового типа, а также треугольные и трапецеидальные функции. В нашем примере выбрана функция принадлежности трапецеидального типа. График функции принадлежности muX(x) изображен на рисунке 2.
Как известно, в нечетком множестве в отличие от классических множеств каждый элемент может принадлежать множеству частично. Степень принадлежности конкретного элемента x* нечеткому множеству X характеризуется коэффициентом принадлежности muX(x*), являющимся действительным числом и принимающим значение в интервале [0, 1]. Равенство этого коэффициента 1 означает 100-процентную принадлежность элемента x* к множеству X, а равенство 0 – отсутствие элемента x* в множестве X. Отображение всего множества элементов x во множество значений muX(x) образует функцию принадлежности muX(x). В теории нечетких множеств наибольшее распространение получили функции принадлежности гауссового типа, а также треугольные и трапецеидальные функции. В нашем примере выбрана функция принадлежности трапецеидального типа. График функции принадлежности muX(x) изображен на рисунке 2.
Как видно из рисунка 2, область значений x разбита на три зоны: xÎ[xmin, xmax] – зона гарантированно качественных объектов, при попадании в которую технологические инструкции гарантируют отсутствие брака; xx2 – зоны брака; xÎ[x1, xmin), xÎ(xmax, x2] – зоны риска.
Решение задачи расчета значений xmin, xmax основано на технологических инструкциях конкретного предприятия, используемых при проектировании, и обычно затруднений не вызывает.
Величины x1, x2 определяются на основе производственного опыта и физических соображений. Так, например, если в качестве корректируемого параметра x выбрать диаметр ступени вала D1 в первой операции перехода III (см. рис. 1), то очевидно, что значения x1, x2 для этого параметра могут быть определены следующим образом: x1=D3, x2=Dk.
Функция принадлежности muX(x) может быть представлена выражением


Таким образом, при внесении пользователем той или иной корректировки система в состоянии рассчитать значение функции принадлежности этой корректировки соответствующему интервалу и тем самым оценить степень риска попадания нового объекта проектирования в зону брака.
САПР ТП ковки на прессах строится в древовидной форме с выделением точек (узлов) возможных воздействий пользователя. На втором этапе проектирования пользователь анализирует полученный объект управления и при необходимости последовательно вносит корректировки в результаты проектирования. Если значение функции принадлежности для внесенной корректи- ровки равно 0 (зона брака), то она отвергается, в противном случае корректировка принимается и проектирование выполняется заново с учетом предыдущих воздействий. При этом введение в систему понятия функции принадлежности позволяет получить некоторую количественную оценку качества полученного объекта проектирования в целом.
Действительно, пусть R – нечеткое множество допустимых решений задачи проектирования ТП ковки для выбранной поковки (вала); r – элемент из множества R; x1, x2, …, xn – последовательные воздействия пользователя на модель объекта управления. Тогда после воздействия x1 качество спроектированного ТП можно оценить по значению muX(x1), после воздействия x2 – по значению muX(x1)´ muX(x2), а после воздействия xn – по значению выражения muR(r)=muX(x1)´muX(x2)´ … ´muX(xn), где muR(r) – значение функции принадлежности полученного решения множеству R после оказанных воздействий.
Рассмотренная схема построения САПР технологии ковки валов на прессах с использованием аппарата теории нечетких множеств и приближенных рассуждений по существу относится к классу нечетких продукционных систем [6, 7] и позволяет реализовать принципы нечеткого управления [10, 11], что, в свою очередь, повышает устойчивость работы системы в условиях неопределенности.
Литература
1. Коновалов А.В., Арзамасцев С.В., Шалягин С.Д., Муйземнек О.Ю., Гагарин П.Ю. Интеллектуальная САПР технологических процессов ковки валов на молотах // Заготовительные производства в машиностроении. 2010. № 1. С. 20–23.
2. Чесноков В.С., Каплунов Б.Г., Возмищев Н.Е., Плаксин А.В. Разработка и применение программного обеспечения для автоматизированного проектирования и моделирования процессов ковки и горячей штамповки // Кузнечно-штамповочное производство. Обработка материалов давлением. 2008. № 9. С. 36–44.
3. Арзамасцев С.В., Гагарин П.Ю., Коновалов А.В. Проектная парадигма и интерфейс в гибридной САПР технологической подготовки кузнечного производства // Программные продукты и системы. 2013. № 2. С. 215–220.
4. Болтянский В.Г. Оптимальное управление дискретными системами. М.: Наука, 1973. 448 с.
5. Трубин В.Н., Макаров В.И., Орлов С.Н., Шипи- цин А.А., Трубин Ю.В., Лебедев В.А. Система управления качеством проектирования технологических процессов ковки. М.: Машиностроение, 1984. 184 с.
6. Беллман Р., Заде Л. Принятие решений в расплывчатых условиях. Вопросы анализа и процедуры принятия решений. М.: Мир, 1976. 430 с.
7. Рыжов А.П. Элементы теории нечетких множеств и измерения нечеткости. М.: Диалог – МГУ, 1998. 75 с.
8. Gottwald S. Foundations of a set theory for fuzzy sets. 40 years of development. Int. Journ. General Systems, 2008, vol. 37, iss. 1, pp. 69–81.
9. Черепанов Е.В. К вопросу о неопределенности, случайности и нечеткости // Современные научные исследования и инновации. 2011. № 6. URL: ttp://web.snauka.ru/issues/2011/ 10/4811 (дата обращения: 11.01.2014).
10. Шеридан Т.Б., Феррел У.Р. Системы человек–машина: модели обработки информации, управления и принятия решений человеком-оператором. М.: Машиностроение, 1980. 520 с.
11. Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений // ААЭКС. 2008. № 2 (22). С. 28–37.
References
1. Konovalov A.V., Arzamastsev S.V., Shalyagin S.D., Muyzemnek O.Yu., Gagarin P.Yu. Intelligent automated designing systems of technological processes of shaft forging on hammers. Zagotovitelnye proizvodstva v mashinostroenii [Blanking productions in mechanical engineering]. Mashinostroenie Publ., 2010, no. 1, pp. 20–23 (in Russ.).
2. Chesnokov V.S., Kaplunov B.G., Vozmishchev N.E., Plaksin A.V. Software design and application for computer-aided design and modeling the processes of hammering and hot stamping. Kuznechno-shtampovochnoe proizvodstvo. Obrabotka materialov davleniem [Forging-stamping production]. 2008, no. 9, pp. 36–44 (in Russ.).
3. Arzamascev S.V., Gagarin P.Ju., Konovalov A.V. Design paradigm and interface in hybrid forgings CAD. Programmnye produkty i sistemy [Software & Systems]. 2013, no. 2, pp. 215–220.
4. Boltyanskiy V.G. Optimalnoe upravlenie diskretnymi sistemami [Optimal control of discrete systems]. Moscow, Nauka Publ., 1973, 448 p.
5. Trubin V.N., Makarov V.I., Orlov S.N., Shipitsin A.A., Trubin Yu.V., Lebedev V.A. Sistema upravleniya kachestvom proektirovaniya tekhnologicheskikh protsessov kovki [Control system for design quality of hammering technological processes]. Moscow, Mashinostroenie Publ., 1984, 184 p.
6. Bellman R.E., Zadeh L.A. Decision-making in a fuzzy environment. Management Science, 1970, vol. 17, no. 4, pp. B141–B164 (Russ. ed.: Moscow, Mir Publ., 1976, 430 p.).
7. Ryzhov A.P. Elementy teorii nechetkikh mnozhestv i izmereniya nechetkosti [The elements of fuzzy set theory and fuzziness measurement]. Moscow, Dialog – MGU Publ., 1998, 75 p.
8. Gottwald S. Foundations of a set theory for fuzzy sets. 40 years of development. Int. Journ. General Systems. 2008, vol. 37, iss. 1, pp. 69–81.
9. Cherepanov E.V. On uncertainty, random nature and fuzziness. Sovremennye nauchnye issledovaniya i innovatsii [Modern scientific researches and innovations]. 2011, no. 6. Available at: http://web.snauka.ru/issues/2011/10/4811 (accessed Jan. 11, 2014).
10. Sheridan T.B., Ferrell U.R. Man-machine systems: information, control and decision models of human performance. MIT Press Publ., 1975, 452 p. (Russ. ed.: Moscow, Mashinostroenie Publ., 1980, 520 p.).
11. Perederiy V.I., Eremenko A.P. Mathematical models and relevant decision-making algorithms. AAEKS [Automatics. Automation. Electrical engineering complexes and systems]. 2008, no. 2 (22), p. 28–37.




 , определяемый как отношение длины биллета Lb к высоте осаженного слитка Hs:
, определяемый как отношение длины биллета Lb к высоте осаженного слитка Hs: , (1)
, (1) (2)
(2) T=0,6.
T=0,6. определяется из условия (1) по формуле
определяется из условия (1) по формуле  , а минимально допустимая высота
, а минимально допустимая высота 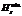 – из условия (2) по формуле
– из условия (2) по формуле  где
где  ; Vs – объем осаженного слитка с учетом угара биллета.
; Vs – объем осаженного слитка с учетом угара биллета.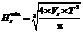 .
. осаженного слитка определяются из условия постоянства объема Vs по формулам:
осаженного слитка определяются из условия постоянства объема Vs по формулам:  ,
, неравенствами
неравенствами (3)
(3) определяется технологическими инструкциями (в операции протяжки обычно равно 2). Величина
определяется технологическими инструкциями (в операции протяжки обычно равно 2). Величина 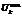 вычисляется по формуле
вычисляется по формуле 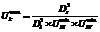 , где
, где  – квадрат наибольшего диаметра ступеней готовой поковки вала,
– квадрат наибольшего диаметра ступеней готовой поковки вала,  – минимально допустимые уковы в III и IV переходах (рис. 1). На практике при ковке валов обычно принимают
– минимально допустимые уковы в III и IV переходах (рис. 1). На практике при ковке валов обычно принимают  ,
, 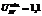 .
. ,
,  .
. .
. на незначительную величину.
на незначительную величину.


