An approach to case-based synthesis of functional programs
Abstract:This article deals with an automatic functional programs synthesis problem. We consider the way to apply case-based reasoning approach to program synthesis. In order to use such framework for our problem we have to consider several subproblems: definition of a "similarity" relation over program specifications space, search of the most suitable known program for a given specification and adaptation of a chosen program to new specification. We will consider adaptation method only in this article and leave other subproblems for further work. We can consider the problem of adaptation as a problem of program correction: we have to modify given (chosen in search procedure) program, so that it will satisfy a given specification. There is a method for functional logic program correction, which have a form of conditional term-rewriting systems. So, our idea is to translate a functional program to term-rewriting system and then apply the correction method to it. In this article we will consider procedures of such translation and adaptation of the correction method for our task.
Аннотация:В данной статье рассматривается проблема автоматического синтеза функциональных программ. Описывается способ применения рассуждений на основе прецедентов в синтезе программ. Для применения этого подхода к задаче необходимо рассмотреть несколько подзадач: определение отношения «похожести» в пространстве спецификаций программ, поиск наиболее подходящей к заданной спецификации известной программы и адаптация выбранной программы к новой спецификации. Авторы рассматривают только подзадачу адаптации, оставив остальные подзадачи для дальнейшей работы. Задачу адаптации можно рассматривать как коррекцию программы, то есть модификации выбранной в ходе поиска программы таким образом, чтобы она удовлетворяла заданной спецификации. Существует метод коррекции функционально логических программ, имеющих вид системы переписывания термов с условиями. Таким образом, идея авторов состоит в трансляции функциональной программы в систему переписывания термов и в применении к ней известного метода коррекции. В данной статье рассматриваются процедура такой трансляции и адаптация метода коррекции для поставленной задачи.
| Fastovets N.N. (nnf-cmc@cs.msu.ru) - Lomonosov Moscow State University (аспирант ), Москва, Россия | |
| Keywords: term rewriting system, case based reasoning, program correction, program synthesis, artificial intelligence |
|
| Ключевые слова: term rewriting system, case based reasoning, program correction, program synthesis, artificial intelligence |
|
|
|
|
@Nowadays we can see significant growth of automation in wide range of human activities and processes [1]. This builds up a new level of software development requirements: programming must be quicker, as cheap as possible and provide needed level of produced programs quality. So, these conditions make software development process automation actual. Such automation is partially achieved by existing high-level programming languages. However, increasing of abstraction level requires significant complication of translation (and/or compilation) algorithms. So, we meet the problem of automatic program synthesis here. It is automatic or automated construction of executable program by formal specification that can also be executable. The main advantage of automatic synthesis is a possibility to manipulate an effect (computation) instead of tool (programming language). Using of LINQ queries to objects (enumerable collections) instead of for and foreach loops in modern versions of .Net framework [2] can be considered as a rough example of such change. There are several different methods of automatic synthesis which can be classified in three approaches [1]: deductive synthesis, where a specification is represented via theorem over input and output variables, and a program can be obtained from the proof of the theorem; inductive synthesis, where a specification is represented as a set of input-output examples and a program can be constructed by them; transformational synthesis, where a synthesis procedure must construct a new version, which is optimized by some measure. Also, there are some little-bit unusual approaches, like generation of program as game strategy [3]. But most of these approaches are not very useful in practice that makes further research actual. At the same time, there is an interesting bio-inspired approach to intelligent problem solving. It is case-based reasoning (CBR) [4]. Roughly speaking, the main idea of CBR is using known solutions for new tasks. In general, problem solving with CBR includes steps of so-called 4-Re’s cycle: Retrieving, Reusing, Revising and Remaining. When CBR system receives a new task T it performs search of most similar task T¢ in case-memory (Retrieving step). Then, the system can reuse information from known solution S¢ of T¢ and try to apply this information for constructing the solution S for the task T. Next, a system has to check an obtained solution S and add a new case (T, S) to case-memory for further solutions. This approach can be very useful in such problem domains which have no efficient theory, applicable for problem solving (e.g. medicine). We share an opinion [5] that CBR could be useful for a program synthesis problem. But we have to solve several issues of case-based reasoning application: how to define “similarity” measure for tasks (programs specification), how to organize case-memory for an efficient search of the most similar case and how to adapt a chosen case (program) for a given task. Obviously, search procedure is closely related to adaptation method, because we want to perform successful adaptation of a chosen case to a new task. Due to this, we restrict this work to the adaptation method only and leave studying of search procedure for future work. So, in this paper attracts attention to the method of known case adaptation to a new task. Our cases are known programs and the tasks are formal specifications – first order logic clauses which express requirements to the synthesized program behavior. In program synthesis we can consider adaptation procedure as correction: for a new given specification S1 search procedure chooses program P2 that satisfies its specification S2; if P2 satisfies S1, then system can return P2 as an answer. But we expect that P2 does not satisfy S1 and, hence, it can be considered as incorrect implementation for S1, that has to be corrected. Correction here is a transformation of P2 to a new certain program P1 that satisfies S1. In this paper we consider functional programs (functions) and show adaptation of functional-logical programs correction method for such functions. Preliminaries We are going to describe base concepts and propositions of the synthesis method in this section. First of all, we will describe the concepts of functional and functional logic programs, terms narrowing and relations between functions and term rewriting systems. Functional and functional logic programs. We consider of functional programs synthesis. These are programs created from constants and variables occurs, functional calls (including recursive calls) and conditional branching. This paradigm is close to mathematical concept of functions. Semantics of functional programs is mapping from input space to output values space. Functional logic (FL) languages are extensions of functional languages with logic programming principles [6, 7]. Computing in FL-programs is based on a narrowing process that is generalization of term rewriting process. We need to describe several definitions here. Conditional term rewriting systems [7, 8] are a computation model for rule-based languages [7]. Term rewriting system defined as a pair of R and Σ sets. Σ is a set of functional symbols f1/n1, …, fk/nk, where ni is an arity of function fi. R is a set of rules: {(li®riÜCi}. We can split Σ on two disjointed subsets Σ=FÈC where F is a set of so-called defined functional symbols and C is a set of constructive symbols. A functional symbol f/n is defined if and only if R contains a rule of form (λ→ρ) where λ has form f (t1, …, tn) and t1, …, tn are some terms. C is a complement to F in Σ. Constructive term is a term of form c(t1, …, tn) where c/n is a constructive symbol and t1, …, tn are constructive terms. We use several special denotations: for t term t½u is a subterm of t on the position u; t[r]½u is a term t, where a subterm of t on the position u is replaced by ρ. Let R be a program and g be a goal. We say that g is conditionally narrows into g' if there is a position u in g, a standardized apart variant of rule r=(λ→ρ)<< to express that a s can be obtained from Functional logic programs are a powerful tool for solving equations. For an equation e[
where In this work we are going to confront functional programs with functional logic programs. For every functional program f (x1, …, xN) that computes output value Correctness of programs. We say that a program is correct if it computes required output values for given values of input parameters. We say that functional program f ( We say that functional logic program R satisfies a specification of the intended semantics set IR, if and only if Oca(R) Í IR and IR Í Oca(R). Since the intended semantics set for R can be represented as another functional logic program RSpec, we can say that R satisfies RSpec if Oca(R) Í Oca(RSpec) and Oca(RSpec) Í Í Oca(R). Functional logic programs correction. Correction of programs using base method, described in [7], is performed by iterative application of so-called unfolding operator. Unfolding is defined as follows. Let R be the program. 1. Suppose r1, r2 << R are rules, such that r1 = =(l1 ® p1 Ü C1) and r2 = (l2 ® p2 Ü C2). The rule unfolding of r1 with relation to r2 is 2. Suppose r << R. The program unfolding of r is defined as: UR(r) = (R È Ur¢ÎR Ur¢ (r)) \ {r}. Next several definitions are required for correction process description. We say, that rule r is unfoldable with relation to R if and only if UR(r) ¹ R \ {r}. We say, that rule r is discriminable if and only if r is unfoldable and it occurs in narrowing derivation for at least one e Î Ep. The top-down correction algorithm that we use as a base for our adaptation technique is follows. Input data for processing are sets of positive and negative examples, and a program that we want to correct. 1. If program does not narrow any positive example, we finish the procedure. The program cannot be corrected (with the considering method). 2. Initialize current form of program R0 with R. 3. Enter the main loop of algorithm – unfolding phase. While there is a rule r in Ri that is used for derivation positive and negative example, we choose a discriminable rule r¢ in Rj and construct a new version of program |Ri+1 = UR(r). 4. After unfolding step a deletion phase starts. We remove all rules from Ri, which are used for derivation of negative examples computation. 5. Then, correction procedure returns obtained program Ri as a correct version. Now, we are ready to describe our adaptation of the functional logic program correction method to functional programs. Correction of functional programs In general, the main workflow of the proposed method contains follow steps. 1. Translation of given function φ to the term rewriting system form. Source function y = φ(x) computes output value y from a specified values of input arguments. We can construct a term-rewriting system (TRS) that solves equation φ(x) = y for the instantiated values of x and apply the original method for correction of such TRS. Then, thus corrections will be mapped to φ, and obtained function φ' would be returned as answer of system. 2. Computation of negative examples set. We suspect that specification at this step is already represented as a set of examples. So, our task here is to construct positive and negative examples set from that. 3. Correction of the obtained Rφ w.r.t. sets of positive and negative examples. This step consists in application of the base top-down unfolding-based correction algorithm to the obtained program and examples. The result of such correction is a new program Rcφ. 4. Translation of the obtained Rcφ to a functional program, which can be computed in usual way. At the final step we translate obtained correct term-rewriting system Rcφ, that solves equations of form φ'(x) = y, to the function φ'(x), that satisfies given specification. This function will be returned as answer of the system. Translation of a function to a term rewriting system. At this step we construct an equivalent functional-logic program for given functional program. First of all, we define a values representation method. Since we will work with TRS, it is easier to represent numbers via special functions. For natural numbers we use function s(x), that returns “next” value for the argument: s(0) = 1, s(s(0)) = 2, … For integer values (with negative values) we introduce function d(x) (additional to s(x)), which returns “previous” value for the argument: d(0) = –1, d(d(0)) = –2, … Real values could be represented via special function dv(x, y), that represents relation of arguments x and y: dv(s(0), s(s(0)))=1/2, dv(d(d(0)), s(s(s(0))))=2/3, … With this representation we can define, for example, less-or-equal relation as follows: 0 £ 0®true; 0 £ s(x) ® ® true; 0 £ d(x) ® false; s(x) £ 0 ® false; d(x) £ 0 ® true; s(x) £ s(y) ® x £ y; d(x) £ d(y) ® x £ y; s(x) £ d(y) ® false; d(x) £ s(y) ® true. Also, we will use denotation sk(x) and dk(x) for short representation of positive and negative numbers k respectively: s3(0) will be a short denotation of s(s(s(0))). In addition to this numbers representation, we also introduce the special function switch(w, x, y) for representation of conditional branching, where w represents condition or result of condition evaluation, x and y represent true and false branches respectively. Definition of switch is obvious: switch(true, x, y) ® x; switch(false, x, y) ® y. Now we are ready to describe translation procedure. The first step of our correction process is translation of given functional program body to a equivalent functional logic program in form of term rewriting system. We split the given function to a set of components, which correspond to nodes of abstract syntactic tree of the target function body. These components can represent variables, function calls, constants (as special case of functional calls for 0-arity functional symbols) and conditional branching points. The main idea of the translation procedure is to represent these components via rules in obtained TRS: left hand sides of such rules have to represent these components and right hand sides has to describe the process of values computation for corresponding components. Next, since main elements of correction in base method are narrowing rules, we are interested in more detailed components splitting. For that we propose follow procedure. Assume we have a function φ( 1. First of all, we put a rule φ(x1, …, xn) ® E[x1, …, xn] in Rφ. 2. For each rule r = (l®r) in Rφ we perform follow transformations: a. if r º ift1 then t2 else t3, we replace r in Rφ by r¢ º (l®switch(t1, t2, t3)); b. if 3. If Rφ did not change during previous step, we finish translation procedure, else we return to the second step. 4. Next, we add to Rφ definition of the function switch(w, x, y) and other non built-in functions (in general, all used functions excluding s(x), d(x) and dv(x, y)). In order to illustrate this translation, we can consider following example. Assume we want to construct term rewriting system that represents the function pow (x, k) = if k > 0 then x ´ pow(x, k – 1) else 1. After first step of translation we obtain Rpow = {pow(x, k)® if k > 0 then x ´ pow(x, k – 1) else 1}. First iteration of step 2 with rule (a) gives us Rpow = {pow (x, k)® switch (k > 0, x ´ pow(x, k – 1), 1)}. Since Rpow has been changed, we repeat step 2. Now we will apply rule (b) and obtain Rpow = {pow(x, k)® ® switch(k>0, y1(x, k), 1); y1(x, k) ® x ´ pow(x, k–1)}. We just replaced subclause pow(x, k – 1) by call of the new function y1(x, k) and added a new rule y1(x, k) ® x ´ pow(x, k – 1) in Rpow. Next step in the same way gives us
Then, new iteration of step 2 will not change Rpow and we can go to step 4 and add a simple definition of the functions switch and >. So, we obtain final form of program
The functional logical program obtained during our translation process can be analyzed using the base method of correction. For that we have to split a given examples set to sets of positive and negative examples and then apply the described top-down correction algorithm. Separation of examples. We suspect that correction will work with specifications, which are represented by sets of computation examples. Such examples can be obtained from specification in form of CTRS [7], while the last can be constructed from clause of some assertion language [9]. That deals with general idea of our synthesis process: source program is taken from case-memory after execution of search procedure. Obviously, that sets of examples are an interesting base for similarity measure between cases: when user gives a set of examples to a system, the most similar case is the function, which closes the biggest part of these examples. So, we need to separate these examples into positive and negative sets. We achieve this just by application of the program to left hand sides of examples and comparing the result with corresponding right hand sides. So, we have a set of examples E = {li = ri}, where li = j( For every example e we can construct (by application of R) the derivation sequence DR(e) = e1 and occurring rules set OR (DR(e)) = Application of the top-down algorithm. Proceed to the next step in main phase of program correction. We apply the base top-down correction algorithm to the program Rφ, that represents source function φ, and the positive and negative examples sets Er and En respectively, given by user. The first condition of the algorithm application is that the considering program has to derive at least one positive example. It was checked at (unconsidered) step of most similar case search and, besides that, at the examples set separation step. The initial form of the considering program (denoted as R0) is our program Rφ itself. First phase of the algorithm is consecutive search of a discriminable rules and unfolding them with relation to a current form of the program Ri. At each step of this phase we check Next phase is deletion: we remove all rules that are used in derivation of negative examples and return the obtained form of the program Rc. Translation of TRS to function. At the previous step we obtained the corrected version of the term rewriting system that represents the source function. Now, we have to restore a function from the obtained TRS. This procedure is similar unfolding, but we apply all applicable rules to right-hand side of the first rule simultaneously. Thus, the abstract program R = ={f(x) ® switch (g(x, 0), y1(x), y2(x)); y1(x) ® ®s(s(x)); y2(x) ® d (d (x))} shall take form of the function: f (x) = if g (x, 0) then s (s (x)) else d (d (x)). Conclusion In this article we considered an adaptation of functional logic programs correction method to the correction of functional programs. This method can be used at reusing step of bigger program synthesis system that uses case-based reasoning approach. There are several problems that restrict applicabi- lity of the method for synthesis tasks: a specification has to be given in form of examples, instead of compact first-order logic clause in deductive synthesis method; the system has to perform main loop several times; the correct answer is not guaranteed; and some others. But we hope that considering of functional programs from term-rewriting point of view could be an efficient way for solution of a synthesis problem. So, our future work will be directed to solving this problems and integration of these methods in case-based program synthesis system. References 1. Kreitz C. Program Synthesis. Chapter III.2.5 of Automated Deduction – A Basis for Applications. Kluwer Publ., 1998, pp. 105–134. 2. Magennis T. LINQ to Objects Using C# 4.0: Using and Extending LINQ to Objects and Parallel LINQ (PLINQ). Addison-Wesley Professional Publ., 2010, 336 p. 3. Kugler H., Segall I. Compositional synthesis of reactive systems from live sequence chart specifications. Proc. of the 15th int. conf. on tools and algorithms for the construction and analysis of systems: held as part of the joint European Conferences on theory and practice of software (Proc. TACAS '09). ETAPS, Berlin, Springer-Verlag Publ., Heidelberg Publ., 2009, pp. 77–91. 4. Aamondt A., Plaza E. Case-based reasoning: foundational issues, methodological variations, and system approaches. AI Communications. 1994, vol. 7, no. 1, pp. 39–59. 5. Gomes P., Pereira F., Paiva P., Seco S., Carreiro P., Ferreira J., Bento C. Using CBR for automation of software design patterns. Proc. of the European Conf. on Base-Based Reasoning (ECCBR’02). Cambridge, 2002. 6. Hanus M. The integration of functions into logic programming: from theory to practice. Journ. of Logic Programming. 1994, vol. 19&20, pp. 583–628. 7. Alpuente M., Ballis D., Correa F., Falaschi M. An integrated framework for the diagnosis and correction of rule-based programs. Theoretical Computer Science archive. Elsevier Science Publ. Ltd. Essex, UK, 2010, vol. 411, iss. 47, pp. 4055–4101. 8. Klop J.W., de Vrijer R. Extended term rewriting systems. Conditional and Typed Rewriting Systems. Lecture Notes in Computer Science. 1991, vol. 516, pp. 26–50. 9. Comini M., Gori R., Levi G. Assertion based inductive verification methods for logic programs. Electronic Notes in Theoretical Computer Science. 2001, vol. 40, pp. 52–69. Литература 1. Kreitz C. Program Synthesis. Chapter III.2.5 of Automated Deduction – A Basis for Applications. Kluwer Publ., 1998, pp. 105–134. 2. Magennis T. LINQ to Objects Using C# 4.0: Using and Extending LINQ to Objects and Parallel LINQ (PLINQ). Addison-Wesley Professional Publ., 2010, 336 p. 3. Kugler H., Segall I. Compositional synthesis of reactive systems from live sequence chart specifications. Proc. of the 15th int. conf. on tools and algorithms for the construction and analysis of systems: held as part of the joint European Conferences on theory and practice of software (Proc. TACAS '09). ETAPS, Berlin, Springer-Verlag Publ., Heidelberg Publ., 2009, pp. 77–91. 4. Aamondt A., Plaza E. Case-based reasoning: foundational issues, methodological variations, and system approaches. AI Communications. 1994, vol. 7, no. 1, pp. 39–59. 5. Gomes P., Pereira F., Paiva P., Seco S., Carreiro P., Ferreira J., Bento C. Using CBR for automation of software design patterns. Proc. of the European Conf. on Base-Based Reasoning (ECCBR’02). Cambridge, 2002. 6. Hanus M. The integration of functions into logic programming: from theory to practice. Journ. of Logic Programming. 1994, vol. 19&20, pp. 583–628. 7. Alpuente M., Ballis D., Correa F., Falaschi M. An integrated framework for the diagnosis and correction of rule-based programs. Theoretical Computer Science archive. Elsevier Science Publ. Ltd. Essex, UK, 2010, vol. 411, iss. 47, pp. 4055–4101. 8. Klop J.W., de Vrijer R. Extended term rewriting systems. Conditional and Typed Rewriting Systems. Lecture Notes in Computer Science. 1991, vol. 516, pp. 26–50. 9. Comini M., Gori R., Levi G. Assertion based inductive verification methods for logic programs. Electronic Notes in Theoretical Computer Science. 2001, vol. 40, pp. 52–69. |
http://swsys.ru/index.php?id=3850&lang=.docs&page=article |
|

 by narrowing derivation with R.
by narrowing derivation with R. ]º(s[
]º(s[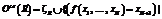
 ,
, is a set of reflexivity axioms for constructive symbols ci occurring in R, and x1, …, xN+1 are distinct variables.
is a set of reflexivity axioms for constructive symbols ci occurring in R, and x1, …, xN+1 are distinct variables. for specified values of the arguments
for specified values of the arguments  we can construct a functional logic program Rf that solve equations of form f(x¢1, …, x¢N) = y with specified values of arguments x1, …, xN+1. In other words, Rf has to narrow left hand side of such equations to a computed value of f function.
we can construct a functional logic program Rf that solve equations of form f(x¢1, …, x¢N) = y with specified values of arguments x1, …, xN+1. In other words, Rf has to narrow left hand side of such equations to a computed value of f function. satisfies a specification S=P[
satisfies a specification S=P[ , which satisfy precondition P, the expression E[
, which satisfy precondition P, the expression E[
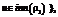 where y is a new variable.
where y is a new variable.
 we introduce new function y(x1, …, xk), where k £ m is count of different variables, occurring in g-headed subterm, replace r in Rφ by l®f (t1, …, ti, y(p1, …, pk), … tn) and add a new rule
we introduce new function y(x1, …, xk), where k £ m is count of different variables, occurring in g-headed subterm, replace r in Rφ by l®f (t1, …, ti, y(p1, …, pk), … tn) and add a new rule 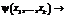
 in Rφ.
in Rφ. .
. .
. e2 … en
e2 … en  true
true We will use this concepts later, during correction algorithm, but note, that examples separation phase gives us initial DR(e) and OR (DR(e)) for each example
We will use this concepts later, during correction algorithm, but note, that examples separation phase gives us initial DR(e) and OR (DR(e)) for each example  in the specification.
in the specification. sets for each example e Î Er È En and perform unfolding for a discriminable rule and check intersection of them: if there are no rules that are used in derivation of a positive as well as a negative examples.
sets for each example e Î Er È En and perform unfolding for a discriminable rule and check intersection of them: if there are no rules that are used in derivation of a positive as well as a negative examples.