Анализ интервально стохастических температурных полей технических систем
| Мадера А.Г. (alexmadera@mail.ru) - НИИСИ РАН (профессор, зав. отделом), г. Москва, Россия, доктор технических наук, Кандалов П.И. (petrki87@gmail.com) - НИИСИ РАН (зам. зав. отделом), Москва, Россия | |
| Ключевые слова: температурное поле, неопределенный, интервальный, стохастический, математическое ожидание, дисперсия, среднее квадратическое отклонение |
|
| Keywords: a tempering, uncertainty, interval, stochastic, mathematical expectation, variance, standard deviation |
|
|
|
|
Реальные температурные поля технических систем, как показывает практика, не являются строго определенными и детерминированными, а носят неопределенный, а точнее интервальный характер. Иными словами, температура в каждой точке технической системы может принимать любые значения внутри некоторых интервалов своего изменения. Неопределенный характер температурных полей технических систем обусловлен неопределенным характером факторов, определяющих тепловой режим технической системы. Их можно условно разбить на три группы: факторы конструкции технической системы, факторы, возникающие при функционировании технической системы, и факторы окружающей среды.
Неопределенность конструктивных факторов технической системы обусловлена следующим. В структуру любой технической системы, как правило, входят серийно изготавливаемые элементы. Параметры и характеристики конструкции этих элементов (размеры, состояния поверхностей, волнистости, неровности, неплоскостности и пр.) в силу неизбежного статистического технологического разброса различаются между собой. Понятно, что параметры и характеристики конкретного элемента в серии «идентичных» элементов являются вполне определенными и могут быть измерены с определенной точностью, однако все элементы в совокупности принадлежащих серии однородных элементов одного и того же вида будут обладать различными параметрами и характеристиками, изменяющимися внутри некоторых интервалов своих статистических допустимых значений. Кроме того, конструктивные сопряжения элементов друг с другом (взаимное расположение, зазоры, площадь контакта, характер контакта и пр.) при монтаже и установке элементов в технической системе подвержены статистическому технологическому разбросу, свойственному любому способу монтажа, сборки, креплениям и т.д. Поэтому техническая система, созданная из различных серийно изготавливаемых элементов, также будет иметь параметры и характеристики, носящие неопределенный характер и изменяющиеся в пределах некоторых интервалов. Вторая группа факторов, обусловливающих неопределенный интервальный характер параметров теплового режима, включает в себя факторы, возникающие и во время функционирования отдельных элементов в системе, и в технической системе в целом (мощности потребления элементов, мощности тепловыделения, тепловые потоки в элементах и между элементами и т.д.). Эти факторы в силу статистического технологического разброса изготовления тоже носят неопределенный характер и изменяются внутри интервалов своих возможных значений. К факторам окружающей среды, вызывающим неопределенность температурных полей технических систем, относятся температура окружающей среды, напряжение внешнего электропитания, скорости и входные температуры тепло- и хладоносителей, условия охлаждения и теплоотвода отдельных элементов и технической системы в целом. Все эти факторы носят случайный характер. К ним относятся еще собственно среда (воздух, жидкость, вакуум, космос), факторы включения и/или взаимодействия рассматриваемой технической системы с другими техническими системами, которые, в свою очередь, отличаются неопределенностью своих параметров и характеристик, а также характер эксплуатации технической системы (наземные, воздушные, водные, подвижные, стационарные и пр.). Таким образом, температурные поля в технических системах носят неопределенный интервально стохастический характер, обусловленный, во-первых, статистическим технологическим разбросом параметров и характеристик элементов как при их изготовлении, так и при монтаже и установке в технической системе, во-вторых, статистическим разбросом параметров и характеристик элементов и всей технической системы в целом при функционировании и, в-третьих, случайным характером условий окружающей среды. Существующие методы моделирования температурных полей технических систем исходят из допущения, что параметры, определяющие тепловые режимы, являются детерминированными, иначе говоря, все данные, определяющие протекание теплового процесса и его характер в технической системе, являются полностью известными и однозначно определенными. Между тем практика показывает, что такое допущение дает весьма далекие от действительности результаты, и это обусловлено, как показано выше, такими факторами, как статистический технологический разброс изготовления «идентичных» систем и их элементов, случайность при функционировании технической системы, случайный характер параметров окружающей среды. Случайный характер факторов, определяющих тепловой режим технических систем, приводит к тому, что различные экземпляры «идентичных» технических систем, построенных на «идентичных» элементах, будут иметь различное распределение температуры и, как следствие, в силу зависимости от температуры – различные эксплуатационные параметры и характеристики. Все случайные факторы, определяющие тепловой режим технической системы, изменяются внутри интервалов своих допустимых значений, поэтому их неопределенность носит интервальный стохастический характер, равно как и неопределенность распределений температуры в системе. Какие именно значения внутри интервалов изменения примут те или иные параметры в каждом конкретном экземпляре системы и/или элемента, априори неизвестно, однако границы интервалов, как правило, известны, по крайней мере, всегда могут быть установлены, например, из приемо-сдаточных испытаний или предварительного моделирования элементов. Моделирование интервально стохастических температурных полей необходимо не только для повышения адекватности моделирования. Зачастую причиной неправильного функционирования и срабатывания системы, выхода из строя, потери устойчивости, уменьшения помехозащищенности и надежности является выход эксплуатационных и функциональных параметров за пределы допустимых интервалов изменения [1]. Проблема моделирования стохастических температурных полей в технических системах неоднократно рассматривалась в научной литературе, например в [2–4]. Вместе с тем до сих пор нет адекватных и эффективных математических и компьютерных методов моделирования интервально стохастических температурных полей в технических системах. Это обусловлено как значительными математическими трудностями, связанными со стохастическими матрицами большой размерности и операциями с ними (обращение, проблема определения стохастических собственных векторов и значений и пр.), так и априори неизвестной сходимостью искомых распределений и моментов стохастического температурного поля к своим истинным «точным» значениям. В настоящей работе развивается метод математического и компьютерного моделирования интервально стохастических температурных полей, обусловленных интервальным стохастическим характером входных данных, определяющих тепловые режимы технической системы. Входные данные представляют собой случайные величины, равномерно распределенные внутри интервалов своего изменения. Метод и алгоритм математического и компьютерного моделирования интервально стохастических температурных полей в технических системах основывается на трех подходах: матрично-топологическом методе авторов [5, 6], компьютерной реализации с помощью разработанного авторами программного комплекса (STF-ElectronMod [5, 7]) и частично на методе статистических испытаний [8]. Применение метода на практике показало его эффективность с точки зрения как затрат машинного времени, так и адекватности получаемых результатов. Сравнение разработанного метода с методами, реализуемыми в интервальном анализе (см., например, [9, 10]), показало, что результаты, получаемые с помощью интервальной арифметики, приводят к неоправданно широким интервалам температур, не адекватным реальности. Применение разработанного метода показано на примере моделирования интервально стохастического температурного поля в электронной системе. Метод и алгоритм моделирования интервально стохастических температурных полей Параметры и характеристики технической системы q(ω) = (q1(ω), q2(ω), …, qn(ω)), определяющие тепловой режим (коэффициенты теплопроводности материалов конструкции, коэффициенты теплоотдачи с поверхностей элементов и системы, температуры среды внутри и снаружи, мощности тепловыделений, контактные тепловые сопротивления и другие параметры и характеристики конструкции, функционирования и эксплуатации технической системы) в общем случае изменяются в пределах своих интервалов, принимая в них с равной вероятностью любое значение, где ω – элементарные события из пространства элементарных событий Ω (ωÎΩ). Иначе говоря, они носят интервально стохастический характер и могут моделироваться посредством случайных величин, подчиняющихся равномерному закону распределения вероятностей. Это означает, что все параметры и характеристики qi(ω) технической системы из вектора q(ω), будучи интервально стохастическими, изменяются в интервалах qi(ω)Î[ В силу интервально стохастического характера параметров и характеристик технической системы решение уравнений стохастической математической модели, описывающей температурное поле, будет интервально стохастическим полем T(ω) = = T(x, y, z, ω). При этом температура в каждой точке технической системы будет изменяться в некотором интервале и иметь распределение ве- роятностей, вообще говоря, отличное от равномерного. В результате решения стохастической математической модели определяются поля статистических мер (математических ожиданий, дисперсий, средних квадратических отклонений, границ интервалов) стохастического температурного поля T(x, y, z, ω) в технической системе: – поле математических ожиданий (МО) температур – поле дисперсий D(x, y, z) рассеяния случайных значений температур вокруг математического ожидания; – поле средних квадратических отклонений (СКО) ϭ(x, y, z) температурного поля, D(x, y, z) = = ϭ2(x, y, z); – поле нижней границы Tн(x, y, z) и верхней границы Tв(x, y, z) интервалов стохастического температурного поля T(x, y, z, ω), ω Î Ω, в пределах которых изменяются все отдельные случайные реализации температур для ω Î Ω в каждой точке технической системы. Поля границ интервалов Tн(x, y, z) и Tв(x, y, z) являются в то же время границами доверительных интервалов, которые с некоторой доверительной вероятностью Рдов покрывают возможные значения истинных температур в технической системе и могут встречаться на практике. При этом нижние и верхние границы интервалов температур в точках (x, y, z) вычисляются как Tн(x, y, z) = = Метод математического и компьютерного моделирования интервально стохастических температурных полей, как уже говорилось, основан на матрично-топологическом методе моделирования трехмерных температурных полей многослойных структур [5, 6], компьютерной реализации в виде программного комплекса (ПК) моделирования трехмерных детерминированных температурных полей электронных систем (STF-ElectronMod) [5, 7] и методе статистических испытаний [8]. Алгоритм метода (графически представлен на рисунке) включает три основных этапа. Этап 1. Вводятся исходные данные, в полной мере характеризующие конструкцию, функционирование и условия эксплуатации технической системы и определяющие ее тепловой режим. Входные данные, являющиеся интервально стохастическими, задаются в виде нижних и верхних границ интервалов своего изменения. По введенным данным рассчитываютя усредненные температуры и мощности всех элементов в технической системе. Расчеты проводятся по матрично-топологическому методу с помощью ПК расчета детерминированных температур STF-ElectronMod. С помощью процедуры метода статистических испытаний производится разыгрывание множества реализаций стохастических входных данных и накапливаются реализации рассчитанных величин усредненных температур элементов и мощностей источников и стоков тепла в технической системе. Этап 2. Множество накопленных реализаций температур служит для вычисления статистических мер усредненных температур и мощностей элементов в технической системе: МО; дисперсий (D); средних квадратических отклонений (СКО); границ (нижней и верхней) интервалов, внутри которых изменяются реализации усредненных температур и мощностей; ковариационной матрицы стохастической связи между мощностями активных элементов (источников тепловыделения) и пассивных (стоков тепловых потоков). Этап 3. Определяются температурные поля статистических мер в технической системе: поля математических ожиданий, дисперсий, средних квадратических отклонений, границ интервалов, покрывающих при заданной доверительной вероятности возможные значения стохастических температур, которые могут иметь место на практике. Данный алгоритм положен в основу разработанного авторами ПК STF-ElectronMod-2014, предназначенного для анализа интервальных стохастических температурных полей технических систем. Комплекс реализован для персональных компьютеров и для процессора с частотой не менее 1,5 Ггц, позволяет осуществлять вычисления полей статистических мер температуры в достаточно сложной технической системе при числе статистических реализаций 10 000 и точности моделирования, не превышающей 3 %, в пределах 2–3 минут. Пример применения к электронной системе Разработанный метод был применен для компьютерного моделирования интервально стохастических температурных полей в электронной системе (ЭС), представляющей собой электронный модуль, включающий многослойную печатную плату (МПП) с 13 чередующимися сигнальными и полиимидными слоями и установленными на ее поверхности 5 интегральными микросхемами (ИМС) в керамических корпусах различных типов. Условия эксплуатации: свободный конвективный теплообмен с воздушной средой, нормальное давление, температура 25 °С и кондуктивный теплоотвод с торцов ЭС. Моделирование интервально стохастического температурного поля ЭС проводилось в условиях интервальной неопределенности мощностей потребления ИМС Pимс, тепловых сопротивлений корпусов ИМС Rjc и монтажных воздушных зазоров δ между корпусами и МПП. В таблице приведены результаты моделирования: статистические меры интервально стохастических значений температур (МО и СКО) корпусов ИМС, а также интервалы значений температур корпусов теплонагруженных ИМС (№№ 1–5). Результаты моделирования наглядно показывают, что реальные значения температуры (см. табл., последний столбец) корпусов ИМС не являются однозначно определенными и детерминированными, а представляют собой интервальные стохастические температуры. Они изменяются в соответствующих интервалах, имеющих в ряде случаев довольно большой размах. Так, разброс реальных температур ИМС № 1 (см. табл.) может достигать ±22 °С, что составляет ±21 % относительно значения МО (101,9 ºС). Результаты моделирования Modeling results
Полученные результаты свидетельствуют о том, что возможные значения температуры корпусов ИМС, установленных в различных экземплярах одного и того же типа ЭС, с вероятностью Рдов, не меньшей 0,9 (ϰ=3), будут заключены в интервалах, приведенных в таблице. Так, реальные значения температуры корпуса ИМС № 1 в реальных ЭС находятся в интервале [80,1 ºС; 123,6 ºС], а для ИМС № 4 – в интервале [45,6 ºС; 55,0 ºС]. В связи с этим ориентирование разработчиков ЭС на некоторое значение детерминированной температуры, получаемое посредством существующих методов теплового моделирования, является неадекватным и далеким от практики, что зачастую приводит к серьезным ошибкам при проектировании ЭС, которые впоследствии скажутся при испытаниях и эксплуатации ЭС, вплоть до невыполнения возложенных на них задач. Разработанный подход, при котором моделирование температурных полей технических систем проводится в условиях неопределенных интервально стохастических входных данных, адекватно описывает реальные температуры, имеющие место на практике. В то же время детерминированный подход, применяемый в настоящее время при моделировании температурных полей технических систем, не отвечает реальным данным, имеющим место на практике, поскольку действительные значения температур носят принципиально неопределенный интервальный характер. Необходимо отметить, что попытки моделировать неопределенности в виде простых интервалов с использованием правил интервальной арифметики приводят к неоправданно широким интервалам температур и некорректным результатам, поскольку интервальные операции существенно зависят от последовательности вычислений и алгебраических преобразований. Описанный в статье метод показал свою эффективность при тепловом проектировании различных реальных ЭС. Литература 1. Надежность технических систем: справочник; [под ред. И.А. Ушакова]. М.: Радио и связь, 1985. 450 с. 2. Мадера А.Г. Иерархический подход при тепловом проектировании электронных изделий // Программные продукты и системы. 2008. № 4 (84). С. 43–46. 3. Georgiadis J.G. On the approximate solution on non-deterministic heat and mass transport problems. Int. J. Heat Mass Transfer, 1991, vol. 33, no. 8, pp. 2099–2105. 4. Keller C.J., Antonetti V.W. Statistical thermal design for computer electronics. Electronic Packaging and Production, 1979, vol. 19, no. 3, pp. 55–62. 5. Мадера А.Г., Кандалов П.И. Матрично-топологический метод математического и компьютерного моделирования температурных полей в электронных модулях: программный комплекс STF-ElectronMod // Программные продукты и системы. 2012. № 4. С. 160–164. 6. Кандалов П.И., Мадера А.Г. Моделирование температурных полей в многослойных структурах // Программные продукты и системы. 2008. № 4. С. 46–49. 7. Кандалов П.И., Мадера А.Г. Simulation of Temperature Fields of Electronic Modules 2013 (STF-ElectronMod 2013). Свид. о госрегистрации прогр. для ЭВМ № 2013615400. 8. Михайлов С.М., Ермаков Г.А. Статистическое моделирование. М.: Наука, 1982. 9. Алефельд Г., Херцбергер Ю. Введение в интервальные вычисления. М.: Мир, 1987. 10. Шарый С.П. Конечномерный интервальный анализ. Н.: Изд-во XYZ, 2012. References | |||||||||||||||||||||||||||||||||||||||||||||||||||
http://swsys.ru/index.php?id=3896&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Программный комплекс моделирования стохастических температурных полей в технических системах STF-ElectronMod
- Концепция математического и компьютерного моделирования тепловых процессов в электронных системах
- Моделирование температурных полей в многослойных структурах
- Программы моделирования температурных полей в изделиях плоской формы
- Математическое моделирование теплофизических процессов в слоистых структурах

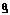 ,
, ], где
], где  ;
; –ϰ·ϭ(x, y, z) и Tв(x, y, z)=
–ϰ·ϭ(x, y, z) и Tв(x, y, z)=