Параллельные алгоритмы вычисления локальных минимумов целочисленных решеток
| Кузьмин О.В. (quzminov@mail.ru) - Институт математики, экономики и информатики Иркутского государственного университета (профессор, зав. кафедрой ), Иркутск, Россия, доктор физико-математических наук, Усатюк В.С. (L@Lcrypto.com) - Братский государственный университет, г. Братск (аспирант ), Братск, Россия | |
| Ключевые слова: метод ленстра–ленстра–ловаса, блочный метод коркина–золотарева, поиск крат-чайшего вектора, поиск кратчайшего базиса, целочисленные решетки, приведение базиса решетки |
|
| Keywords: block korkin–zolotarev reduction, block korkin-zolotarev reduction, , shortest basis problem, integer lattices, lattice basis reduction |
|
|
|
|
Математический аппарат теории решеток тесно связан с абстрактной и геометрической алгебрами, числовыми методами приближенного ана- лиза, теорией информации, оптимизацией и криптоанализом, что позволяет применять методы теории решеток для решения ряда задач: линейного программирования, плотной упаковки тел (в частности, сфер в евклидовом пространстве) [1], факторизации многочленов с рациональными коэффициентами [2], поиска диофантовых приближений [3], оптимизации кодирования с использованием адаптивных антенных решеток со слабо коррелированными антенными элементами (MIMO) [4] и многих других [5–9].
Основные понятия и обозначения Определение 1. Решеткой называется дискретная абелева подгруппа, заданная в пространстве Rn. Пусть базис B={b1, …, bn} задан линейно независимыми векторами в Rm. Тогда под решеткой будем понимать множество целочисленных линейных комбинаций этих векторов:
где m и n – размерность и ранг решетки соответственно, m³n. Определение 2. Решетки, у которых размерность и ранг равны, называются полными. Определение 3. Решетки L1 и L2, заданные базисами Множество конгруэнтных решеток может быть получено в результате умножения базиса B решетки на целочисленные унимодулярные матрицы. Определение 4. Пусть L – решетка ранга n. i-м соответствующим минимумом, где i=1, 2, …, n, называется точная нижняя граница радиусов замкнутых шаров с центром в нуле, содержащих i линейно независимых векторов решетки L:
где Длине кратчайшего вектора в решетке L соответствует l1(L), что приводит непосредственно к формулировке задачи поиска кратчайшего и короткого векторов в решетке. Определение 5. Задача поиска короткого вектора (D-short vector problem, SBPg(m)): пусть дана m-мерная решетка L(B) ранга n и вещест- венное D>1. Найти нетривиальный вектор, в D раз больший кратчайшего вектора в решетке При g=1 решается задача поиска кратчайшего вектора в решетке, при g>1 – короткого вектора. Определение 6. Константой Эрмита называется величина gm, заданная выражением
Применяя первую теорему Минковского о соответствующих минимумах, с одной стороны, и лемму о норме кратчайшего вектора в решетке, получим соответственно верхнюю и нижнюю оценки длин кратчайшего вектора в решетке:
где Определение 7. Задача поиска короткого базиса решетки (D-short basis problem, SBPg(m)): пусть дан базис полной решетки B и вещественное D>1. Найти базис
При g=1 полученный базис достигает нижней границы неравенства Адамара и является ортогональным: Определение 8. Базис B={b1, …, bm} решетки LÌRm приведен по длине, если в результате ортогонализации решетки методом Грамма–Шмидта выполняется следующее неравенство:
где mi,j – коэффициенты Грамма–Шмидта. Определение 9. Упорядоченный по длине базис B={b1, b2, …, bm} решетки LÌRm приведен блочным методом Коркина–Золотарева с блоком bÎ[2, m] и точностью Определение 10. Базис решетки приведен по Ленстра–Ленстра–Ловасу (LLL-алгоритмом), если он приведен блочным методом Коркина–Золотарева с размером блока b=2 и точностью ортогонализации Определение 11. Локальным минимумом решетки называем вектор b={b1, b2, …, bn}, bÎL, для которого справедливы неравенства: ½ci½£½bi½, " b=(c1, c2, …, cm)ÎL, i=1, …, n, при этом хотя бы одно из них строгое. В теории оптимальных сеток Коробова такие векторы образуют узлы оптимальных сеток. Нетрудно убедиться, что эти векторы являются кратчайшими в решетке, а подмножество локальных минимумов образует кратчайший базис решетки. Число всевозможных конфигураций, которые образуют кратчайшие базисы для m-мерной решетки L объема detL, не превосходит величину Таким образом, задача поиска локальных минимумов содержит в себе задачу поиска кратчайшего базиса, известную как алгоритм приведения базиса решеток. На настоящий момент неизвестны полиномиальные алгоритмы приведения базиса по Минковскому, за исключением решеток размерности 2, предложенных Гауссом [12], и 3, предложенных Валле (с кубической сложностью) [13] и улучшенных Семаевым, снизившим сложность до квадратичной [14]. В работе [15] описан алгоритм для приведения базиса по Минковскому до 6 измерений. В работе [16] результат был улучшен до 7-мерных решеток. По причине высокой вычислительной сложности практический интерес имеют алгоритмы поиска локальных минимумов с полиномиальной, псевдо- и субэкспоненциальной сложностью. Для приведения базиса решетки по Ловасу применяется полиномиальный LLL-алгоритм, предложенный в [17]. Для приведения по Коркину–Золотареву применяется блочный метод SE BKZ, предложенный Шнором–Охнером [18]. При изменении размера рассматриваемой подрешетки b и параметра точности ортогональности базиса d получаем иерархию методов от приведения по Ленстра–Ленстра–Ловасу до блочного метода Коркина–Золотарева (см. табл.). Построим, варьируя размер приводимого базиса b и релаксируя норму в блочном методе Коркина–Золотарева, параллельный алгоритм поиска локального минимума целочисленной решетки. На основании нижней оценки из определения 6 нетрудно убедиться, что поиск локального минимума условно состоит из двух алгоритмов ортогонализации базиса и поиска кратчайшего вектора в некоторой решетке [19]. Осуществим декомпозицию и распараллеливание этих алгоритмов. Параллельный алгоритм ортогонализации решеток Классический метод Грама–Шмидта, применяемый для ортогонализации базиса решетки, требует порядка 2mn2 или 2n3 (при m=n) операций с плавающей запятой. Однако классический метод Грама–Шмидта численно неустойчив вследствие ошибок округления [20]. По этой причине на практике в последовательной реализации алгоритмов применяют модифицированный метод Грама–Шмидта [21]. Последний, как и классический метод Грама–Шмидта, обладает сходной вычислительной сложностью. Однако будучи рекурсивным по своей сути, алгоритм Грама–Шмидта обладает неглубокой декомпозицией данных на уровне компонентов вектора при наличии множества блокировок. Эта особенность приводит к неэффективности параллельных реализаций, которая была продемонстрирована в работе [22], производительность в лучшем из случаев не превосходила 60 % от пиковой производительности на матрицах размера 6 000´6 000 для SCI-кластера на 16 XEON 2 ГГц и 37 % для Beowulf-кластера (CLiC) с 528 Pentium III 800 МГц. Схожий результат был получен для параллельных алгоритмов ортогонализации Грама–Шмидта, реализованных на видеокартах NVIDIA CUDA 295 (1 800 Гфлопс при однократной и 150 Гфлопс при двукратной точности вычисления) на матрицах размера 4 000´4 000 Перейдем от традиционно используемого метода ортогонализации Грама–Шмидта к системе эквивалентных определений на основе QR-методов ортогонализации. Определение 12. QR-разложением базиса решетки называют представление матрицы
В свою очередь, верхнюю треугольную матрицу можно представить в виде
Таким образом, ортогонализация Грама–Шмидта связана с QR-разложением следующим образом: В таком случае традиционные определения методов приведения могут быть переформулированы в форму, использующую параллельные QR-методы ортогонализации. Определение 13. Базис решетки L(B), образованный векторами Определение 14. Базис решетки L(B) приведен по Ловасу [17], если он приведен по длине и для коэффициентов R QR-разложения базиса решетки B выполняется условие Определение 15. Базис решетки L(B) приведен по (Эрмиту)–Коркину–Золотареву (HKZ, KZ) [25], если он приведен по длине и для всех квадратных подматриц R¢ размера n–i+1, 1£i<n, полученных из R вычеркиванием i первых строк и столбцов; первый вектор-столбец является кратчайшим в решетке L¢(R¢), Опираясь на указанные определения, авторы провели сравнение методов ортогонализации базисов решетки с использованием библиотек линейной алгебры для многоядерных процессоров AMD CORE MATH Library, Intel Math Kernel Library и видеоускорителей NVIDIA CUDA CUBLAST, AMD OPENCL CLMAGMA, Accelerated Parallel Processing Math Libraries (CLAMDBLAS) (см. рис. 1, 2). Кривые отображены на рисунках сверху вниз в порядке их упоминания в легенде. Видеоускоритель GPU NVIDIA 550 TI (691 Гфлопс при однократной и 58 Гфлопс при двукратной точности вычисления, то есть видеокарте с почти в три раза меньшей производительностью) дает 30-кратный прирост в случае использования метода поворота Гивенса на видеокарте и почти 170-кратный прирост при использовании метода отражений Хаусхолдера на четырех ядрах Phenom X4 965 3.4 ГГЦ [26]. Однако следует отметить, что применение полученных методов затруднено следующими обстоятельствами. С ростом размерности решетки рост необходимой точности представления чисел с плавающей запятой невысок для ансамблей случайных решеток [18]. В случае применения базисов, соответствующих плотным рюкзачным задачам [27] или же решеткам, сложным по Гольдштейну–Майеру [28, 29], необходимая точность арифметики растет линейно (см. рис. 3). Последнее обстоятельство существенно затрудняет использование видеоускорителей. Так, падение пиковой производительности арифметики двукратной точности по сравнению с однократной – 1 к 4 для специализированных вычислительных ускорителей и 1 к 24 для массовых видеокарт. С дальнейшим ростом точности вычислений обменное отношение резко возрастает. С другой стороны, с ростом размерности решетки время, затрачиваемое на ортогонализацию базиса, становится небольшим по сравнению со временем поиска кратчайшего (короткого) вектора в подрешетке. Однако следует отметить, что в случае применения некоторых вероятностных методов, в частности, основанных на отсечении веток при поиске кратчайшего вектора в подрешетке [30, 31], применение параллельных методов ортогонализации становится актуальным при приведении решеток высоких размерностей. Параллельный алгоритм Решение задачи поиска кратчайшего вектора в решетке заключается в полном переборе всех линейных комбинаций векторов базиса
где Формализуя задачу, получим обход дерева от корня к листу, в каждой из вершин которого решается соответствующее линейное уравнение. Из корня этого дерева выходит
а в случае предварительного приведения базиса решетки
Далее приведем параллельный алгоритм поиска кратчайшего вектора в решетке L(B), B={b1, b2, …, bm}: Вход: Выход: Вектор x=(x1, x2, …, xm)ÎZm: 1. Вычислить xm–k координатных компонент на k уровнях от корневого узла. 2. Каждый из потоков перебирает свое поддерево xm, …, xm–k, i£m–k.
Если если Если Если 3. Возвращаем вектор с минимальной нормой из множества X. Данный алгоритм был реализован на основе потоковой модели NPTL (Native POSIX Thread Library [32]) под CentOS 6.3. При осуществлении приведения 103-мерной решетки BKZ-методом при b=52, 4 потоках, исполняемых на AMD Phenom 965/8 Gb DDR2-800, получено трехкратное ускорение выполнения метода по сравнению c fplll-4.0.1 [33]. Предложенный метод позволяет перебирать порядка 10 миллионов координатных компонент в секунду. Было проведено сравнение с реализациями паралелльного алгоритма поиска кратчайшего вектора на видеокартах CUDAENUM [34] и многоядерных мультипроцессорных конфигурациях parENUM [35]. Для сравнения применялась следующая тестовая конфигурация: fplll-4.0.4, parENUM, pLRT: AMD Phenom II X4 965 3.4Ghz/8Gb DDR2-800|12.5 ГБ/c, ОС CentOS 6.4 (2.6.32-358.6.2.el.x86_64). Пиковая производительность SP 108.8; DP 54.4 Гфлопс. Для ParENUM применялись пакеты mpich2-dev x86_64 1.3.2p1-1.fc16, mprf-3.1.2, gmp.x86_64 4.3.1-7.el6_2.2. Для CUDAENUM Intel Core i7-3930K, 64GB DDR3-2133 (16.5 ГБ/c), GTX 680 2Gb SP 3090; DP 129 Гфлопс (192 ГБ/C), ОС CentOS 6.4 (2.6.32-358.14.1.el.x86_64), NVIDIA CUDA SDK 5.5x64. Приводились решетки, сложные по Гольштейну–Майеру. Чтобы производительность видеокарты не упала вследствие необходимости применения четырехкратной точности и производительность не упиралась в шину памяти, применялись сравнительно малые размеры подрешетки и значительно более мощные конфигурации рабочей станции. Результаты сравнения представлены на рисунке 4. С использованием приведенных алгоритмов было реализовано приложение, занявшее 1-е и 3-е места на международном конкурсе алгоритмов поиска коротких векторов [36], для норм
Таким образом, в работе предложен параллельный алгоритм решения задачи поиска локальных минимумов в целочисленных решетках на основе блочного метода Коркина–Золотарева. Приведены точностные характеристики метода при решении задач приближенного поиска кратчайшего вектора и базиса в целочисленной решетке. Выполнено сравнение алгоритма и его аналогов. Реализованный на основе предложенного алгоритма программный комплекс установил мировой рекорд на международном конкурсе поиска кратчайших векторов на ансамблях решеток, построенных на кольце кругового многочлена, сложных по Гольштейну–Майеру.
Литература
1. Conway J.H., Sloane N.J.A. Sphere Packings, Lattices and Groups. Springer. 3rd ed., 1999, 703 p. 2. Dwork C. Lattices and their Application to cryptography [Lecture Notes]. Stanford Univ., 1998, 116 p. 3. Grotschel M., Lovasz L., Schrijver A. Geometric Algorithms and Combinatorial Optimization. Springer-Verlag, 1993, 564 p. 4. Mobasher A. Applications of Lattice Codes in Communication Systems. Canadian theses. Univ. of Waterloo. Dept. of Electrical and Computer Engineering, 2008, 147 p. 5. Bernstein D.J., Buchmann J., Dahmen E. (Eds.) Post Quantum Cryptography. Springer, 2009, pp. 147–191. 6. Darte A., Schreiber R., Villard G. Lattice-based memory allocation Computers, IEEE Transactions, 2005, no. 10 (54), 7. Lagarias J.C., Odlyzko A.M. Solving low-density 8. Коробов Н.М. Приближенное вычисление кратных интегралов с помощью методов теории чисел // Докл. Акад. наук СССР. 1957. Т. 115. № 6. С. 1062–1065. 9. Коробов Н.М. Теоретико-числовые методы в приближенном анализе. М.: Изд-во МЦНМО, 2004. 288 с. 10. Press W.H., Teukolsky S.A., Vetterling W.T. Numerical Recipes: The Art of Scientific Computing. NY: Cambridge Univ. Press, 2007, 1262 p. 11. Быковский В.А. О погрешности теоретико-число- 12. Gauss C.F. 1801. Disquisitiones Arithmeticae. Leipzig; Translated into English by A. C. Clarke. New Haven, CT: Yale Univ. Press, 1966. 13. Vallee B. Une Approche Geometrique de la Reduction de Reseaux en Petite Dimension. PhD Thesis, Univ. de Caen, 1986. 14. Semaev I. A 3-dimensional lattice reduction algorithm. Lecture Notes in Computer Science, Springer-Verlag. 2001, 15. Рышков С.С. К теории приведения положительных квадратичных форм по Эрмиту–Минковскому. Исслед. по теории чисел. 2, Зап. научн. сем. ЛОМИ, 33. Л.: Наука, 1973. 16. Afflerbach L., Grothe Н. Calculation of Minkowski-reduced lattice bases. Computing, 1985, no. 3–4 (35), pp. 269–276. 17. Lenstra A., Lenstra H., Lovász L. Factoring polynomials with rational coefficients. Mathematische Annalen, 1982, no. 261 (4), pp. 515–534. 18. Schnorr C.P., Euchner M. Lattice basis reduction: Improved practical algorithms and solving subset Sum Problems. Fundamentals of Computation Theory, 1991, pp. 68–85. 19. Кузьмин О.В., Усатюк В.С. Программный комплекс приведения базиса целочисленных решеток // Программные продукты и системы. 2012. № 4 (100). С. 180–183. 20. Longley J.W. Modified Gram-Schmidt process vs. classical Gram-Schmidt. Communicationsin Statistics – Simulation and Computation. 1981, no. 10 (5), pp. 517–527. 21. Higham N.J. Accuracy and Stability of Numerical Algorithms Society for Industrial and Applied Mathematics, 2002, 711 p. 22. Runger G. and Schwind M. Comparison of Different Parallel Modified Gram-Schmidt Algorithms. Euro-Par 2005, LNCS 3648, pp. 826–836. 23. Milde В., Schneider М. Parallel Implementation of Classical Gram-Schmidt Orthogonalization on CUDA Graphics Cards. TU Darmstadt Fachbereich Informatik Kryptographie und Computeralgebra, 2009, URL: http://www.cdc.informatik.tu-darmstadt.de/~mischnei/ CUDA_GS_2009_12_22.pdf (дата обращения: 20.06.2014). 24. Hermite C. Extraits de lettres de M. Hermite M. Jacobi sur differents objets de la theoriedes nombres.Reine Angew Math. 1850, no. 40, pp. 279–290. 25. Korkine A., Zolotareff G. Sur les formes quadratiques. Maht. Ann., 6, 1873, pp. 366–389. 26. Усатюк В.С. Реализация параллельных алгоритмов ортогонализации в задаче поиска кратчайшего базиса целочисленных решеток. ПДМ. Приложение. 2012. № 5. С. 120–122. 27. Schnorr C.P., Shevchenko T. Solving Subset Sum Problems of Density close to 1 by "randomized" BKZ-reduction. IACR Cryptology ePrint Archive, 2012, 620 p. 28. Goldstein D., Mayer A. On the equidistribution of Hecke points. Forum Mathematicum., 2003, vol. 15, no. 2, pp. 165–189. 29. Кузьмин О.В., Усатюк В.С. Комбинаторная оценка мощности множества, содержащего кратчайший вектор, образованного базисом решетки, приведенной блочным методом Коркина–Золотарева. URL: http://arxiv.org/abs/1302.4062 (дата обращения: 20.06.2014). 30. Schnorr C.-P., Horner H.H. Attacking the Chor-Rivest cryptosystem by improved lattice reduction. Springer-Verlag, LNCS, 1995, vol. 921, pp. 1–12. 31. Gama N., Nguyen P., Regev O. Lattice Enumeration using Extreme Pruning. Advances in Cryptology – EUROCRYPT 2010. 29th Conf. on the Theory and Applications of Cryptographic Techniques, 2010, Springer, pp. 257–278. 32. Kerrisk M. The Linux Programming Interface: A Linux and UNIX System Programming Handbook. No Starch Press, 2010, 1552 p. 33. Application fplll. URL: http://perso.ens-lyon.fr/damien. 34. Application GPIENUM. URL: http://homes.esat.kuleuven. 35. Application parENUM. URL: http://xpujol.net/ (дата обращения: 20.06.2014). 36. Ideal lattice challenge. URL: http://www.latticechallenge. |
http://swsys.ru/index.php?id=3959&lang=.docs&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:


 ,
,  , конгруэнтны; L1(B) @ L2(B¢), если объемы фундаментальных параллелепипедов, образованных их базисами, равны: det(L1)= det(L2), где
, конгруэнтны; L1(B) @ L2(B¢), если объемы фундаментальных параллелепипедов, образованных их базисами, равны: det(L1)= det(L2), где  или detL = ½detB½ для полноразмерных решеток.
или detL = ½detB½ для полноразмерных решеток.
 – замкнутый шар радиуса r с центром в нуле.
– замкнутый шар радиуса r с центром в нуле. .
.

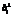 – ортогональный вектор, полученный из базиса одним из QR-методов разложения матрицы базиса решетки: Грама–Шмидта, поворота Гивенса или преобразования Хаусхолдера [10].
– ортогональный вектор, полученный из базиса одним из QR-методов разложения матрицы базиса решетки: Грама–Шмидта, поворота Гивенса или преобразования Хаусхолдера [10].


 , если базис B приведен по длине или
, если базис B приведен по длине или  i=1, …, m, где l1(Li) – длина кратчайшего вектора в решетке Li, образованной ортогональным дополнением векторного пространства с базисом bi, …, bmin(i+b–1, m).
i=1, …, m, где l1(Li) – длина кратчайшего вектора в решетке Li, образованной ортогональным дополнением векторного пространства с базисом bi, …, bmin(i+b–1, m). .
. , C(n) – некоторая положительная константа [11].
, C(n) – некоторая положительная константа [11].
 размера m´n в виде произведения Q-унитарной и R-верхней треугольной матриц:
размера m´n в виде произведения Q-унитарной и R-верхней треугольной матриц:

 , где qi – i-й вектор-столбец ортогональной матрицы Q.
, где qi – i-й вектор-столбец ортогональной матрицы Q. называют приведенным по длине (ослабл. по Эрмиту) [24], если для коэффициентов верхней треугольной матрицы R, QR-разложения базиса решетки B выполняется
называют приведенным по длине (ослабл. по Эрмиту) [24], если для коэффициентов верхней треугольной матрицы R, QR-разложения базиса решетки B выполняется  .
. , 1<i£n, dÎ(0,25, 1].
, 1<i£n, dÎ(0,25, 1]. .
.


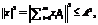 xiÎZ, где A – норма искомого кратчайшего вектора. В качестве нормы берется верхняя оценка длины кратчайшего вектора,
xiÎZ, где A – норма искомого кратчайшего вектора. В качестве нормы берется верхняя оценка длины кратчайшего вектора,  , где gm – константа Эрмита, в тех случаях, когда наименьший из векторов в базисе решетки превосходит A,
, где gm – константа Эрмита, в тех случаях, когда наименьший из векторов в базисе решетки превосходит A,  . По этой причине предварительное приведение базиса решетки позволяет уменьшить пространство перебора xi. С этой целью распишем базис решетки через ортогональные векторы, для простоты изложения используя метод ортогонализации Грама–Шмидта. Получим
. По этой причине предварительное приведение базиса решетки позволяет уменьшить пространство перебора xi. С этой целью распишем базис решетки через ортогональные векторы, для простоты изложения используя метод ортогонализации Грама–Шмидта. Получим  2£i£m, 1£j<i£m, где mi,j – коэффициенты Грама–Шмидта. Легко убедиться, что в этом случае поиск кратчайшего вектора сводится к решению системы неравенств:
2£i£m, 1£j<i£m, где mi,j – коэффициенты Грама–Шмидта. Легко убедиться, что в этом случае поиск кратчайшего вектора сводится к решению системы неравенств:
 , и выбору одного из целочисленных векторов, у которого норма скалярного произведения с базисом решетки минимальна.
, и выбору одного из целочисленных векторов, у которого норма скалярного произведения с базисом решетки минимальна.
 ветвей,
ветвей, ветвей. В силу симметричности дерева (по свойствам нормы) для получения искомого кратчайшего вектора необходимо перебрать только половину его вершин. В результате полного обхода от корня к листу получим предполагаемый кратчайший вектор x с нормой, меньшей либо равной искомой. Если норма полученного вектора будет меньше заданной ранее, целесообразно обновить ее с целью уменьшения пространства перебора. Алгоритм останавливается, когда завершен обход вершин дерева или в случае поиска короткого вектора получен вектор с достаточной нормой. Каждый из потоков вычисляет свою ветку, исходящую из корня дерева.
ветвей. В силу симметричности дерева (по свойствам нормы) для получения искомого кратчайшего вектора необходимо перебрать только половину его вершин. В результате полного обхода от корня к листу получим предполагаемый кратчайший вектор x с нормой, меньшей либо равной искомой. Если норма полученного вектора будет меньше заданной ранее, целесообразно обновить ее с целью уменьшения пространства перебора. Алгоритм останавливается, когда завершен обход вершин дерева или в случае поиска короткого вектора получен вектор с достаточной нормой. Каждый из потоков вычисляет свою ветку, исходящую из корня дерева. , mi,j.
, mi,j. .
.
 и i=1, то
и i=1, то 
 .
. и i¹1, то i=i–1,
и i¹1, то i=i–1, .
. , то i=i+1, xi=xi+1.
, то i=i+1, xi=xi+1. и
и  соответственно.
соответственно.