Авторитетность издания
ВАК - К1
RSCI, ядро РИНЦ
Добавить в закладки
Следующий номер на сайте
№1
Ожидается:
16 Марта 2024
Подход к моделированию процесса оптимизации параметров эллиптических орбит спутниковой системы
An approach to modeling of parameters optimization for satellite system elliptical orbits
Дата подачи статьи: 02.12.2014
УДК: 004.4:62.503.5
Статья опубликована в выпуске журнала № 1 за 2015 год. [ на стр. 87-91 ]Аннотация:В работе предложен подход к моделированию эллиптических орбит спутниковой системы непрерывного обзора поверхности Земли для оптимизации их параметров. С этой целью анализируются варианты решения задачи оптимизации такого обзора спутниковой системой с орбитами эллиптического типа, описываются условия, характеризующие модель движения данной спутниковой системы. Рассматривается кеплеровская модель движения спутника в декартовой (гринвичской) системе координат с началом в центре Земли. При этом для нахождения истинной аномалии используется алгоритм, включающий решение уравнения Кеплера методом последовательных приближений. Дается обоснование критерия оптимальности параметроворбит спутников, системы ограничений оптимизационной задачи. Определяются геоцентрический угловой радиус, изменяющийся с течением времени при полете искусственного спутника Земли от своего перигея к апогею, и угол обзора спутника. Выбрана критериальная функция, пред-ставляющая собой геоцентрическое угловое расстояние между радиус-векторами спутников и текущей точкой земной поверхности в текущий момент времени. Обоснован выбор параметров оптимизации. Учитывая то, что система состоит из групп спутников, движущихся по одной орбите, размерность задачи может быть существенно снижена. Сформулирована в явном виде оптимизационная задача. Проведено моделирование движения спутников в исследуемой спутниковой системе с использованием среды программирования MathCAD2014. В качестве примера на фоне карты Земли построены траектории движения подспутниковых точек трех искусственных спутников Земли с характеристиками, соответствующими характеристикам известной спутниковой системы. Получены зависимости изменения геоцентрической широты и долготы подспутниковых точек от времени, а также визуализировано их движение.
Abstract:This paper proposes an approach to modeling elliptical orbits of the Earth's surface continuous review satellite system to optimize their parameters. For this purpose the author suggests an analysis of options for solving the problemof optimization of such review by a satellite system with elliptic orbits. There are descriptions of the conditions that characterize the motion model of a considered satellite system. The author considers Kepler model of satellite motion in Cartesian (Greenwich) coordinate system with the origin at the center of the Earth. To find the true anomaly the author uses an algorithm that includes a solution of Kepler's equation using a methodof suc-cessive approximations. The paper shows justifying of parameters optimality criterion for satellites orbits, the system of op-timization problem constraints. The author determins geocentric angular radius which changes over time when Earth artificial satellite goes from its perigee to apogee, as well as a satellite viewing angle. The author has selected a criterion function which is a geocentric angular distance between the radius vectors of the satellites and the current point on the Earth's surface at the current time. The choice of optimization parameters is proven. Taking into account the condition thatthe system con-sists of satellites groups and satellites in each group are moving along the same orbit, the problem dimension can be reduced. An optimization problem is stated clearly. The paper shows a satellites motion simulation in the satellite system under re-search using MathCAD2014 environment. As an example, the paper shows the trajectories of the sub-satellite points for three artificial satellites on the Earth map with characteristics corresponding to the characteristics of a known satellite system. The author presents the dependencies of changing the geocentric latitude and longitude of the sub-satellite points from time and visualizes their movement.
| Авторы: Доронкина А.Н. (annadoronkina@bk.ru) - Тверской государственный университет (аспирант), Тверь, Россия | |
| Ключевые слова: оптимизация, критерий оптимальности, не-прерывный обзор поверхности земли, эллиптическая орбита, спутниковая система, среда программирования, моделирование |
|
| Keywords: optimisation, the optimality criterion, , elliptical orbit, satellite system, programming environment, modeling |
|
| Количество просмотров: 15050 |
Версия для печати Выпуск в формате PDF (12.50Мб) Скачать обложку в формате PDF (0.36Мб) |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=3964&page=article |
Версия для печати Выпуск в формате PDF (12.50Мб) Скачать обложку в формате PDF (0.36Мб) |
| Статья опубликована в выпуске журнала № 1 за 2015 год. [ на стр. 87-91 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Метод выбора оптимальной технологии строительства коммуникационного тоннеля
- Методы хранения данных систем видеонаблюдения с использованием грид-технологий
- Вопросы создания АСУ космическими полетами беспилотных аппаратов в околоземном пространстве
- Подход к моделированию, масштабированию и оптимизации работы биореакторов на основании вычислительной гидродинамики
- Методы оптимизации расписаний параллельных обслуживающих систем
Назад, к списку статей



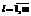 ;
;
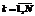 ) в любой момент «видит» на поверхности Земли сферический круг некоторого углового радиуса αk(t) с центром в подспутниковой точке (рис. 1), изменяющийся с течением времени при полете ИСЗ от своего перигея к апогею. Кроме этого, каждый спутник имеет свой угол обзора. Допустим, что угол обзора любого спутника системы данной задачи один и тот же и равен 2γ (рис. 1). Система ИСЗ обеспечивает непрерывный обзор Земли, если любая точка поверхности в любой момент видна хотя бы с одного из спутников [1].
) в любой момент «видит» на поверхности Земли сферический круг некоторого углового радиуса αk(t) с центром в подспутниковой точке (рис. 1), изменяющийся с течением времени при полете ИСЗ от своего перигея к апогею. Кроме этого, каждый спутник имеет свой угол обзора. Допустим, что угол обзора любого спутника системы данной задачи один и тот же и равен 2γ (рис. 1). Система ИСЗ обеспечивает непрерывный обзор Земли, если любая точка поверхности в любой момент видна хотя бы с одного из спутников [1]. системы характеризуется шестью независимыми кеплеровскими элементами [11]: ik – наклонение, Ωk – долгота восходящего узла, ak – большая полуось, ek – эксцентриситет, ωk – аргумент перигея, τk – время прохождения перигея.
системы характеризуется шестью независимыми кеплеровскими элементами [11]: ik – наклонение, Ωk – долгота восходящего узла, ak – большая полуось, ek – эксцентриситет, ωk – аргумент перигея, τk – время прохождения перигея. – множество кеплеровских параметров орбиты k-го ИСЗ {ak, ek, ik, Ωk, ωk, τk}, которые имеют следующее множество допустимых значений Gk:
– множество кеплеровских параметров орбиты k-го ИСЗ {ak, ek, ik, Ωk, ωk, τk}, которые имеют следующее множество допустимых значений Gk: .
. , (1)
, (1)
 ,
, ,
,

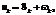
 , где µ – гравитационная постоянная, равная 398620 км3/с2, и его геоцентрическую угловую скорость:
, где µ – гравитационная постоянная, равная 398620 км3/с2, и его геоцентрическую угловую скорость: .
. , вычисляем истинную аномалию ϑk:
, вычисляем истинную аномалию ϑk: 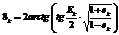 .
.



 .
.
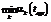 . Поэтому для того, чтобы система осуществляла непрерывный обзор Земли, необходимо и достаточно [1] выполнения неравенства
. Поэтому для того, чтобы система осуществляла непрерывный обзор Земли, необходимо и достаточно [1] выполнения неравенства , (2)
, (2) .
. .(3)
.(3)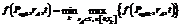 ,
, , то есть решить задачу
, то есть решить задачу ,
, ,
, ,
, 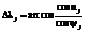 ,
,  , где tΩ – время прохождения ИСЗ экватора в восходящем узле орбиты; ωЗ – угловая скорость вращения Земли, равная 7,29211×10–5 1/c; SΩ – звездное время по Гринвичу в момент прохождения ИСЗ восходящего узла орбиты.
, где tΩ – время прохождения ИСЗ экватора в восходящем узле орбиты; ωЗ – угловая скорость вращения Земли, равная 7,29211×10–5 1/c; SΩ – звездное время по Гринвичу в момент прохождения ИСЗ восходящего узла орбиты.
