При решении проблемы повышения качества электронной компонентной базы [1, 2] критически важных узлов сложных технических систем одной из важных задач является обеспечение однородности партий применяемых электронных изделий. Классификация электронных компонентов по производственным партиям на основе данных неразрушающих тестовых испытаний дана в [3]. Подход с использованием непараметрических моделей [4] позволяет выполнять отбраковку некачественных изделий единственной производственной партии. В данной работе предлагается использовать метод k-средних (k-means) [5–7] для определения центров каждого из кластеров, представляющих собой предполагаемую производственную партию.
Задача k-средних сводится к минимизации следующей целевой функции при известных векторах данных A1, …, An.
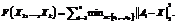 (1)
(1)
Использование метода k-средних предполагает использование ALA-процедуры (Alternating Location-Allocation – изменяющееся размещение-распределение), суть которой сводится к чередованию двух простых шагов.
Алгоритм 1. ALA-процедура.
Дано: векторы данных A1, …, An, k начальных центров кластеров X1, …, Xk.
1. Для каждого центра Xi определить кластер Ci – подмножество векторов данных, для которых центр Xi является ближайшим.
2. Для каждого кластера Ci переопределить его центр Xi:
3. Повторять с шага 1, если хотя бы один кластер изменился на шагах 1, 2.
Использование классического метода k-средних с квадратичной евклидовой мерой расстояния ( ) имеет неоспоримое преимущество: при использовании квадратичной евклидовой меры определение центра кластера представляет собой простейшую задачу, решаемую за один шаг, – определяется среднее значение каждой координаты векторов данных, входящих в кластер, полученные значения являются координатами центра кластера [8].
) имеет неоспоримое преимущество: при использовании квадратичной евклидовой меры определение центра кластера представляет собой простейшую задачу, решаемую за один шаг, – определяется среднее значение каждой координаты векторов данных, входящих в кластер, полученные значения являются координатами центра кластера [8].
Если центр i-го кластера Xi=(xi,1, …, xi,d) – вектор в d-мерном пространстве и векторы данных Aj=(ai,1, …, aj,d),  , соответственно, также имеют d измерений, то новый центр определяется так [8]:
, соответственно, также имеют d измерений, то новый центр определяется так [8]:  .
.
Более сложной является задача с евклидовой метрикой (l2). В этом случае центр кластера представляет собой решение задачи Вебера [8, 9], определяемое с помощью итеративной процедуры Вайсфелда или ее модификаций. Процедура представляет собой алгоритм градиентного спуска [10] и дает приближенное решение задачи.
Надо отметить, что использование вышеперечисленных метрик и мер имеет существенный недостаток с точки зрения интерпретируемости результатов. Задача классификации по производственным партиям ставится с целью как повышения качества электронных узлов путем их комплектации электронными компонентами, произведенными в рамках одной производственной партии и имеющими очень близкие эксплуатационные характеристики, так и дальнейшего взаимодействия с производителем или поставщиком электронных компонентов в направлении повышения качества поставляемой продукции. Если в поставляемой партии обнаружено, что фактически количество производственных партий больше заявленного поставщиком, потребитель электронных компонентов или специализированный испытательный центр должен обосновать отказ в приемке партии изделий.
Требования качества, предъявляемые к электронным компонентам, например в космической отрасли, настолько высоки, что определять принадлежность изделий к одной либо различным производственным партиям приходится по расхождениям (расстояниям) совокупности измерений, едва превышающим точность измерений.
Таким образом, результаты каждого из измерений фактически представляют собой дискретные значения, шаг изменения которых определяется точностью измерительного прибора.
Например, не вдаваясь в физический смысл измеряемых величин, остановимся на некоторых результатах испытаний микросхемы 1526ЛЕ2 по первым семи из 120 измеряемых параметров. В таблице 1 приведены результаты испытаний 14 экземпляров изделий, выбранных из сборной партии из 986 изделий, представляющей собой множество изделий, изготовленных в трех различных производственных партиях.
Как видно из таблицы, значение каждого из измерений колеблется в очень узких пределах.
В частности, для исследуемой сборной партии T1Î{0,001001, 0,001002}, TiÎ{0,0342, 0,0343, 0,0344, 0,0345, 0,0346, 0,0347, 0,0348, 0,0349}, i = 2,7, |T1| = 2, |Ti| = 7. Остальные значения 117 параметров также колеблются в довольно узких пределах. В то же время результат процедуры k-средних (центр кластера) может быть, например, следующим набором значений: T1=0,001001458379, T2=0,03456397208, T3=0,035917650834, …
Точность измерения параметра Т1 составляет 6 знаков после запятой, параметров T2–T7 – 4 знака. Центр кластера представляет собой реальное или смоделированное изделие с идеальными для данного кластера (то есть партии изделий) параметрами. Но точность более 7 и 4 знаков после запятой невозможна из-за отсутствия соответствующих измерительных приборов.
Вследствие этого такой результат кластеризации вызывает недоумение у специалистов. Кроме того, отнесение изделия к тому или иному кластеру (партии) осуществляется по результатам расчета квадратичного евклидова расстояния в нормированном пространстве измерений, в то время как специалисту более понятен диапазон колебания значений параметра в пределах партии.
Возможные методы решения проблемы
Выходом в данной ситуации является применение либо прямоугольной метрики (также именуется манхэттенской метрикой l1), либо метода k-медоид (k-medoids) [11, 12] вместо k-средних.
При использовании метода k-медоид на шаге 2 ALA-процедуры вычисляется не центр кластера, а его медоид – вектор данных, принадлежащий кластеру, такой, что суммарное расстояние от этого вектора до других векторов данных в кластере достигает минимума:  .
.
Такой алгоритм определения минимума достаточно медленно работает, поскольку является комбинаторной процедурой и требует полного перебора всех векторов данных кластера в качестве кандидатур потенциального медоида. Существуют методы аппроксимации данного алгоритма [13–15], неприемлемые в случае, если точность решения особенно важна.
Альтернативой является решение задачи k-средних в прямоугольной метрике. Целевая функция при этом [8] выглядит следующим образом: 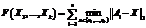 . (2)
. (2)
При работе ALA-процедуры с прямоугольной метрикой каждая из координат центра кластера определяется независимо как медианное значение данной координаты векторов данных, входящих в кластер. Процедуру можно описать следующим образом.
Алгоритм 2. Определение центра i-го кластера (медианы) в метрике l1.
1. Для каждого  :
:
1.1. Отсортировать векторы Ai =(aj,1, …, aj,d)ÎCi по значению k-й координаты, получить последовательность значений  . Здесь ½Ci½ – мощность множества (кластера).
. Здесь ½Ci½ – мощность множества (кластера).
1.2. Рассчитать  Присвоить
Присвоить  . Здесь квадратными скобками обозначена целая часть числа.
. Здесь квадратными скобками обозначена целая часть числа.
1.3. Повторять цикл 1.
2. Возврат  .
.
 Этот алгоритм возвращает значение центра кластера, значение каждой из координат которого совпадает с одним из значений соответствующей координаты векторов данных.
Этот алгоритм возвращает значение центра кластера, значение каждой из координат которого совпадает с одним из значений соответствующей координаты векторов данных.
Например, результат кластеризации выборки, часть которой представлена в таблице 1, на три кластера, выглядит в соответствии с таблицей 2. В таблице в качестве примера приведены значения первых семи измеряемых параметров.
Следует отметить, что набор параметров (значения координат) центра кластера необязательно полностью совпадает с параметрами одного из векторов данных, но значение каждого отдельного параметра обязательно совпадает со значением данного параметра одного из векторов данных (то есть одного из изделий). Соответственно, сохраняется точность значения.
ALA-процедура является алгоритмом локального поиска, ее результаты зависят от выбора начальных центров кластеров. На практике используются следующие варианты запуска ALA-алгоритма:
− многократный запуск из случайно выбранных центров (в качестве центров выбираются векторы данных);
− многократный запуск из центров, выбранных с помощью процедуры k-means++ [16];
− генетические алгоритмы [17, 18] для рекомбинации множеств начальных центров.
Хорошие (по точности и сходимости) результаты показывает генетический алгоритм с жадной эвристикой [19–21]. Данный алгоритм адаптирован к задачам кластеризации электронных компонентов [3]. Алгоритм позволяет применять любой вариант ALA-алгоритма. Здесь мы применим ALA-алгоритм с квадратичной евклидовой мерой и прямоугольной метрикой.
Результаты работы системы классификации с использованием реальных данных
Сравним результаты разбиения партии микросхем 1526ЛЕ2 на 3 предполагаемые производственные партии (3 кластера) с использованием стандартной процедуры k-средних с квадратичной евклидовой метрикой и процедуры с прямоугольной метрикой.
Количество предполагаемых производственных партий будем определять по резкому изменению полученного значения целевой функции (1) или (2) в зависимости от выбранного числа кластеров.
Результаты разбиения на 3 кластера представлены на рисунке 1. Для визуализации кластеров на плоскости использованы процедура MDS (Multi-dimensional Scaling – многомерное масштабирование) [22, 23] и пакеты программ GNUPLOT и ELKI [24].
Изменение значения целевой функции в двух рассматриваемых метриках показано на рисунке 2.

 Как видно из рисунков, обе процедуры дают приблизительно одинаковое разбиение на кластеры. Значения целевой функции также незначительно меняются при переходе от разбиения на 3 кластера к разбиению на 4 кластера и более, что позволяет сделать вывод о наличии 3 производственных партий изделий в сборной партии [3]. В то же время результат процедуры с прямоугольной метрикой дает усредненные значения параметров в каждом кластере, совпадающие со значением соответствующего параметра одного из реальных изделий. На работу каждого алгоритма отводилась 1 минута.
Как видно из рисунков, обе процедуры дают приблизительно одинаковое разбиение на кластеры. Значения целевой функции также незначительно меняются при переходе от разбиения на 3 кластера к разбиению на 4 кластера и более, что позволяет сделать вывод о наличии 3 производственных партий изделий в сборной партии [3]. В то же время результат процедуры с прямоугольной метрикой дает усредненные значения параметров в каждом кластере, совпадающие со значением соответствующего параметра одного из реальных изделий. На работу каждого алгоритма отводилась 1 минута.
Аналогичные результаты были получены для партий других изделий (до 2 511 единиц в партии). При этом количество измерений параметров, используемых при классификации, варьировалось от 16 (диоды) до 230 (большие микросхемы).
В заключение отметим, что применение прямоугольной метрики в задаче классификации электронных компонентов по производственным партиям позволяет получать результаты, аналогичные результатам классической процедуры k-средних. В то же время результаты процедуры кластеризации с применением прямоугольной метрики легко интерпретируются, поскольку полученный результат имеет ту же точность, что и исходные данные тестовых испытаний, используемые при классификации.
Литература
1. Коплярова Н.В., Орлов В.И., Сергеева Н.А., Федо- сов В.В. О непараметрических моделях в задачах диагностики электрорадиоизделий // Заводская лаборатория. Диагностика материалов. 2014. № 80 (7). С. 73–77.
2. Коплярова Н.В., Орлов В.И. Об исследовании компьютерной системы диагностики электрорадиоизделий на основе данных испытаний // Вестн. СибГАУ. 2014. № 1 (53). С. 24–30.
3. Казаковцев Л.А., Орлов В.И., Ступина А.А., Ма- сич И.С. Задача классификации электронной компонентной базы // Вестн. СибГАУ. 2014. № 4 (56). С. 55–61.
4. Коплярова Н.В., Сергеева Н.А. О непараметрических алгоритмах идентификации нелинейных динамических систем // Вестн. СибГАУ. 2012. № 5 (45). С. 39–45.
5. Ackermann M.R. et al. StreamKM: A Clustering Algorithm for Data Streams. J. Exp. Algorithmics, 2012, 17, Article 2.4 published online. URL: http://epubs.siam.org/doi/pdf/10.1137/ 1.9781611972900.16 (accessed 11.01.2015); DOI: 10.1145/ 2133803.2184450.
6. Kanungo T., Mount D., Netanyahux N., Piatko C., Silverman R., Wu A. A Local Search Approximation Algorithm for k-Means Clustering. Computational Geometry, 2004, no. 28, pp. 89–112.
7. Kazakovtsev L.A., Stupina A.A. Fast Genetic Algorithm with Greedy Heuristic for p-Median and k-Means Problems. IEEE 2014 6th Intern. Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT), 6–8 October 2014, St.-Petersburg, 2014, pp. 602–606.
8. Farahani R.Z., Hekmatfar M. (eds). Facility Location Concepts, Models, Algorithms and Case Studies. Springer-Verlag, Berlin Heidelberg, 2009, 550 p.
9. Weiszfeld E. Sur le point sur lequel la somme des distances de n points donnes est minimum. Tohoku Math. Journ., 1937, no. 43 (1), pp. 335–386.
10. Максимов Ю.А., Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования: учеб. пособие. М.: Изд-во МИФИ, 1982. 52 с.
11. Park H.-S., Jun C.-H. A simple and fast algorithm for K-Medoids clustering. Expert Systems with Applications, 2009, no. 36, pp. 3336–3341.
12. Kaufman L., Rousseeuw P.J. Finding groups in data: an introduction to cluster analysis, NY, Wiley Publ., 1990, 368 p.
13. Laucasius C.B., Dane A.D., Kateman G. On k-medoid clustering of large data sets with the aid of Genetic Algorithm: background, feasibility and comparison. Analytica Chimica Acta, 1993, no. 283 (3), pp. 647–669.
14. Zhang Q., Couloigner I. A new and efficient algorithm forr spatial clustering. ICSSA 2005, Singapore, May 9–12, 2005, pp. 181–189.
15. Sheng W., Liu X. A genetic k-medoids clustering algorithm. Journ. of Heuristics, 2006, vol. 12, no. 6, pp. 447–466.
16. Arthur D., Vassilvitskii S. k-Means++: The Advantages of Careful Seeding. Proc. of the Eighteenth Annual ACM-SIAM Symposium on Discrete algorithms, ser. SODA'07, 2007, pp. 1027–1035.
17. Панфилов И.А., Базанова Е.П., Сопов Е.А. Исследование эффективности работы генетического алгоритма оптимизации с альтернативным представлением решений // Вестн. СибГАУ. 2013. № 4 (50). C. 68–71.
18. Vorozheikin A.Yu., Gonchar T.N., Panfilov I.A., So- pov E.A., Sopov S.A. A modified probabilistic genetic algorithm for the solution of complex constrained optimization problems. Vestnik SibGAU, 2009, no. 5, pp. 31–35.
19. Alp O., Erkut E., Drezner Z. An Efficient Genetic Algorithm for the p-Median Problem. Annals of Operations Research, 2003, no. 122 (1–4), pp. 21–42.
20. Kazakovtsev L.A., Antamoshkin A.N. Genetic algorithm with fast greedy heuristic for clustering and location problems. Informatica (Ljubljana), 2014, vol. 38, iss. 3, pp. 229–240.
21. Neema M.N., Maniruzzaman K.M., Ohgai A. New Genetic Algorithms Based Approaches to Continuous p-Median Problem. Netw. Spat. Econ., 2011, vol. 11, pp. 83–99, DOI:10.1007/s11067-008-9084-5.
22. Sun Zh., Fox G., Gu W., Li Zh. A Parallel Clustering Method Combined Information Bottleneck Theory and Centroid Based Clustering. The Journ. of Supercomputing, 2014, no. 69 (1), pp. 452–467. DOI: 10.1007/s11227-014-1174-1.
23. Borg J.F.P. Modern Multidimensional Scaling: Theory and Applications. Springer, 2005, pp. 207–212.
24. Kriegel H.P., Kroeger K.P., Zimek A. Outlier Detection Techniques (Tutorial). 13th Pacific Asia Conf. on Knowledge Discovery and Data Mining (PAKDD 2009), Bangkok, Thailand, 2009, 73 p. URL: https://www.siam.org/meetings/sdm10/tutorial3.pdf (accessed 11.01.2015).



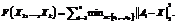 (1)
(1)
 ) имеет неоспоримое преимущество: при использовании квадратичной евклидовой меры определение центра кластера представляет собой простейшую задачу, решаемую за один шаг, – определяется среднее значение каждой координаты векторов данных, входящих в кластер, полученные значения являются координатами центра кластера [8].
) имеет неоспоримое преимущество: при использовании квадратичной евклидовой меры определение центра кластера представляет собой простейшую задачу, решаемую за один шаг, – определяется среднее значение каждой координаты векторов данных, входящих в кластер, полученные значения являются координатами центра кластера [8]. , соответственно, также имеют d измерений, то новый центр определяется так [8]:
, соответственно, также имеют d измерений, то новый центр определяется так [8]:  .
. .
.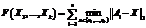 . (2)
. (2) :
: . Здесь ½Ci½ – мощность множества (кластера).
. Здесь ½Ci½ – мощность множества (кластера). Присвоить
Присвоить  . Здесь квадратными скобками обозначена целая часть числа.
. Здесь квадратными скобками обозначена целая часть числа. .
.


